含有一般性热转移过程的低耗散型热机的权衡优化研究∗

卢灿灿 白龙

(中国矿业大学物理学院,徐州 221116)(2016年8月17日收到;2016年9月27日收到修改稿)

含有一般性热转移过程的低耗散型热机的权衡优化研究∗

卢灿灿 白龙†

(中国矿业大学物理学院,徐州 221116)(2016年8月17日收到;2016年9月27日收到修改稿)

实际热机在工作过程中必然伴随热转移过程.本文提出了含有一般性热转移过程的低耗散热机模型.利用权衡优化方法对该低耗散热机的性能进行了优化分析,推导出了权衡判据下热机功率和效率表达式.详细讨论了不同热转移过程支配下的热机功率以及效率特征,其结果有助于深入理解实际热机的优化机制.

低耗散热机,热转移律,权衡判据,热机效率

1 引 言

经济与社会的快速发展导致对能源的需求日益增加,大量能源被消耗的同时伴随着全球变暖和不可再生能源日益枯竭的问题,这对人类的可持续发展提出了严峻挑战.热机是将吸收的热能转变为有用功的装置,在国民生产中发挥着重要作用.自工业革命以来,提高热机的效率和优化热机的性能一直是基础科学和工程领域中普遍关注的问题.热力学第二定律指出,基于卡诺循环而设计的热机的效率ηC=1−Tc/Th,其中Th和Tc分别是高低温热源的温度.虽然基于准静态过程的卡诺热机是理想化的并且其输出功率为零,但是它给出了实际热机执行的上限.1975年,Curzon和Ahlborn[1]基于内部可逆假设,提出了一个唯象的有限时间的卡诺热机模型,并且给出了最大功率时的效率(简称为CA效率),他们的先驱性工作以及之后与其相关的大量研究为有限时间热力学理论的形成奠定了坚实基础.随后,van den Broeck[2]进一步证明了CA效率是线性不可逆热力学理论的一个基本结果,并建立了有限时间热力学与线性不可逆热力学之间的本构关系.

事实上,有限时间热力学框架下的热机性能优化是非常重要的科学问题.传统的热机性能优化通常是构造目标函数方法,基于目标函数与系统参数关系来优化目标函数,进而获得满足热机性能优化的有效方案[3,4].具体表现在:1)基于热机功率和效率的表达式,利用数学分析中的求极值方法获得相应的最大功率和效率的公式,这种方法获得的最大功率与最大效率通常不匹配,即当系统参数满足获得最大功率的条件时,不一定获得最大效率,反之亦然;2)根据最小熵产生原理的热机优化分析,但获得最小熵的表达式不仅需要精细的计算而且非常困难;3)辐射能分析方法,但该方法依赖于环境参数.上述关于热机性能的优化方法通常适用于个例而缺乏普适性.因此,对实际热机的工作过程进行优化必须满足以下原则:1)在以提高热机性能为目的的优化过程中,控制热机工作的参数应具有导向性;2)利用热力学判据优化热机不应该依赖于环境参数;3)应考虑热机工作过程中出现的不可避免的耗散效应.2001年,西班牙的Hernandez等[5]针对热机的优化问题提出了权衡判据方法,该方法通过对所构造的品质函数的分析,能够给出热机在满足最大效率和最小能量损失平衡条件下的工作区域,权衡判据方法提供了一种优化热机性能的统一理论框架,并且在宏观热机和微观热器件的性能优化过程中均得到了广泛应用[6−9].

另一方面,Esposito等[10]根据工质和高低温热源接触过程中的熵产生过程提出了一个低耗散卡诺热机模型,即LD模型,

其中,∆S(＞0)是准静态等温过程中的熵变,τh和τc分别是工质与高低温热源的接触时间,系数Σh和Σc为等温过程中的耗散强度.在对称性耗散情况(Σh=Σc)下,LD模型可以再现CA效率.因此,LD模型提供了理解不同类型热机在最大功率时效率的统一框架.日本学者Izumida等[11−13]推广线性不可逆热力学理论到低阶非线性情形,并提出了最小非线性不可逆热机模型,该模型能够较好地描述有限时间循环热机可能的热耗散效应.作为最小非线性不可逆热机模型的例子,Izumida等[11−13]提出了一个满足线性热转移的热漏项低耗散热机,并且给出了与该模型对应的Onsager系数表达式.然而,我们注意到工质与热源之间的能量转移过程是复杂的,往往受非线性规律的支配.这使得Izumida等[13]提出的基于傅里叶热传导规律(线性规律)的含有热漏的低耗散热机模型不具有普遍性.基于以上论述,本文拓展Izumida等[13]提出的热机模型至一般性情形,并给出含有一般性热漏项的低耗散热机模型.在此基础上,利用权衡判据方法对含有一般性低耗散热机进行优化分析,给出了权衡判据条件下含有一般性热转移过程的低耗散热机功率和效率的表达式,进一步讨论了受不同热转移规律支配的低耗散型热机的优化特征.

2 物理模型和公式

本文研究的含有一般性热转移过程的低耗散性热机模型用如下方程描述:

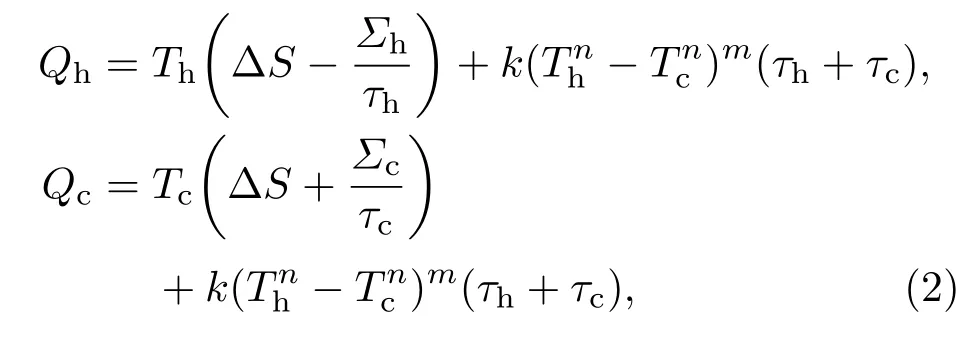
其中,Th和Tc是高低温热源的温度,∆S＞0是等温可逆过程中的熵变,τh和τc为工质分别与高低温热源的接触时间,Σh和Σc表征了工质与高低温热源接触的不可逆过程中的耗散强度.方程(2)的第三项为源于热转移过程的热漏项,k是热导率,热漏项中的指数(m,n)的不同取值反映了不同的热转移过程.当m=n=1时,从方程(2)给出的热机模型可以自然地得到Izumida等[13]提出的含有线性热漏项的低耗散热机模型.因为热机优化的权衡判据方法不依赖于环境参数和无需计算熵产生率,而且能够给出热机在最小能量损失情况下的最大效率.所以,基于优化热机的权衡判据方法构造的目标函数为

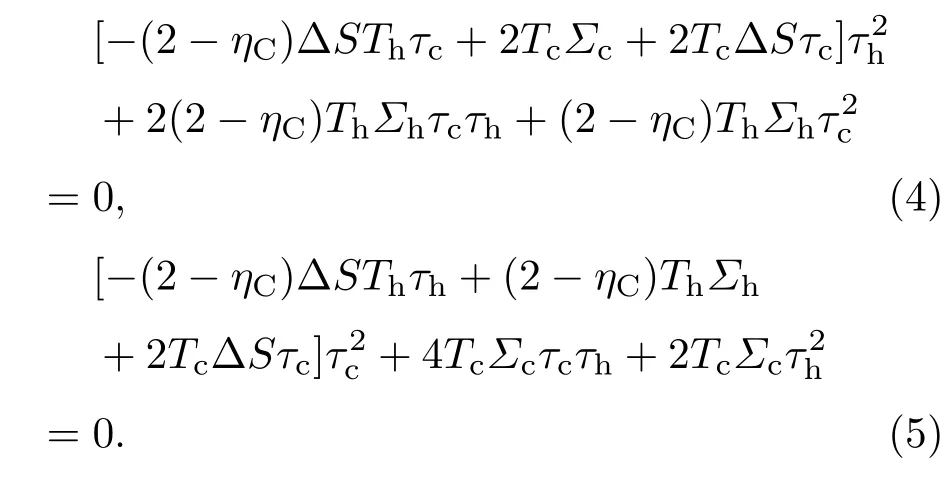
式中,α= τc/τh和β= Σc/Σh.这样,权衡判据下的接触时间可以表示为

将方程(7)和(8)代入热机功率公式P=(Qh−Qc)/(τh+τc),可以获得权衡判据下热机的功率为

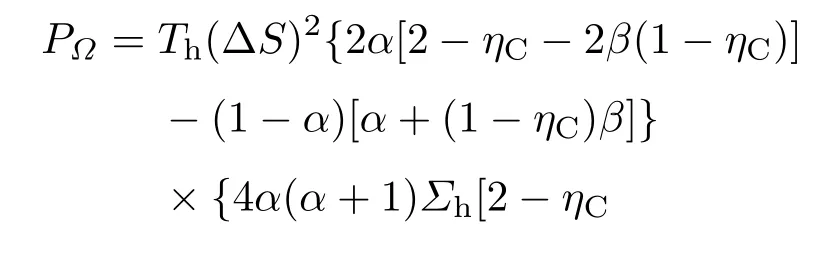
进一步可以得到无量纲功率为

从方程(9)或者(10)可以看出,权衡判据下热机的功率不依赖于非线性热漏项,而与接触时间、耗散项以及卡诺效率有关.同样,根据热机效率公式η=1−Qc/Qh,可以得到权衡判据下热机的效率为

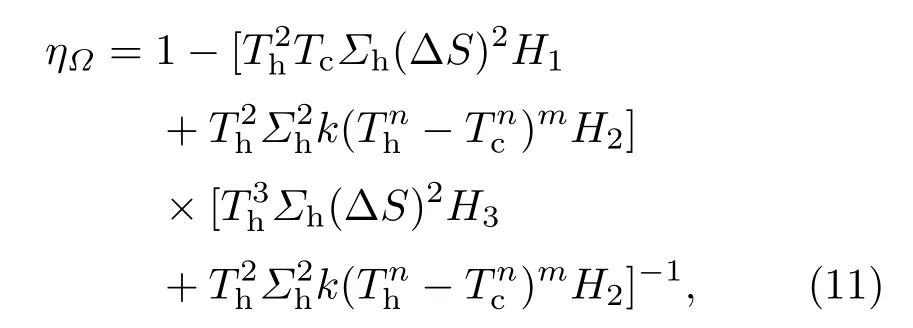
方程(11)中的H1,H2和 H3分别为

当不存在热漏项(k=0)时,权衡判据下的效率为

方程(10),(13)和(14)为进一步深入理解和研究权衡判据下热机的优化特征提供了理论依据.

3 数值计算结果与讨论

接触时间和耗散强度是影响热机功率和效率的重要因素.因此,本节将着重讨论接触时间比α和耗散强度比β是如何影响平衡判据条件下的热机功率和效率的.图1(a)给出了在固定耗散比β情况下功率和卡诺效率的关系曲线,发现随着ηC的增加,功率单调增加.然而,接触时间比的增加导致了功率明显减小.相似的特征也体现在图1(b)中,但值得注意的是当耗散比较小时,热机的工作区域较宽;随着β的增加,热机的工作区域明显减小,而且曲线的非线性特征明显减弱.以上结果说明,α和β过大,热机的输出功率和工作区间明显减小,进而不利于热机的工作执行.

图1 (网刊彩色)(a)当β=0.1而α取不同值时,约化功率PΩ与卡诺效率ηC的关系;(b)当α=0.1而β取不同值时,约化功率与卡诺效率ηC的关系Fig.1.(color on line)(a)Forβ =0.1 and d iff erentα,the reduced powervs the Carnot effi ciency ηC;(b)forα=0.1 and d iff erentβ,the reduced powervs the Carnot effi ciency ηC.

图2 (网刊彩色)当ηC=0.5和k=0时,(a)在改变α情况下,约化效率ηΩ/ηC与β的关系;(b)在改变β情况下,约化效率ηΩ/ηC与α的关系Fig.2.(color on line)ForηC=0.5 and k=0,(a)the reduced effi ciency ηΩ/ηCvsβ with the change ofα;(b)the reduced effi ciency ηΩ/ηCvsα with the change ofβ.

为了更好地揭示热转移过程是如何影响热机工作的,我们首先基于方程(13)研究了权衡判据条件下不含热漏过程的热机效率.基于可逆循环过程的卡诺热机效率是实际热机效率的极限,本文用含热漏的低耗散热机的效率ηΩ与所对应的卡诺效率ηC比值ηΩ/ηC作为物理量来衡量真实热机的优化执行,能够反映出真实热机的效率与理想化热机效率的接近程度,这对于设计和优化实际热机是有帮助的.从图2(a)可以发现,随着耗散比β的增加,热机的效率单调减小;另外,接触时间比α的增加导致了热机效率增加,但约化效率变化的程度较为平缓.图2(b)中ηΩ/ηC-α的关系曲线明显反映出耗散比β的增强减小了热机的工作区域;热机效率随着α单调递增的变化趋势从非线性型逐渐向线性型过渡.实际热机在工作中必然伴随着热转移过程,这在某种程度上影响了热机的效率.相比于k=0时的效率曲线(见图2),存在热转移过程时的热机效率的变化非常显著.

图3给出了含三种热转移过程和不同接触时间比α条件下的ηΩ/ηC与耗散比β的关系曲线.当α较小时,ηΩ/ηC-β呈现出单调递减的变化特征,随着α的增加,ηΩ/ηC-β的单调变化特征逐渐减弱,最终转变为单调递增的行为.值得注意的是,虽然对应于不同的热转移过程,效率曲线的变化行为相似,但是相应效率曲线的数值不同.当n=1和m=1.25时,即热转移过程满足杜龙-玻替定律,对应不同α的效率是最大的,如图3中的实线所示.当热转移过程满足牛顿定律(n=m=1)时,效率值有所降低(见图3中的划线);进一步,当热转移过程满足斯特潘-玻尔兹曼定律(n=4,m=1)时,热机效率的减弱非常显著,如图3中的点划线所示.

图3 (网刊彩色)当ηC=0.5和k0时,在改变α的条件下,约化效率ηΩ/ηC与β的关系,其中,n=1,m=1.25(实线);m=n=1(划线);n=4,m=1(点划线)Fig.3.(color on line)ForηC=0.5 and k/0,the reduced effi ciency ηΩ/ηCvsβ with the change ofα:n=1,m=1.25(solid lines);m=n=1(dashed lines);n=4,m=1(dash-dotted lines).

图4给出了对应于三种典型的热转移过程以及不同耗散比β时的热机效率与接触时间比α的关系曲线.发现权衡判据下的ηΩ/ηC随着α变化的呈现出明显的非线性特征,即随着α的增加而达到极大值,然后逐渐减弱的变化趋势.进一步发现耗散比β的增加导致了热机可工作区域的减小,同时热机效率的极大值右移.另外,比较图4(a)—(c)可以看出,随着m的减小和n的增加,相应的热机效率值明显减弱.上述结果表明,不同的热转移过程极大地影响了热机性能.

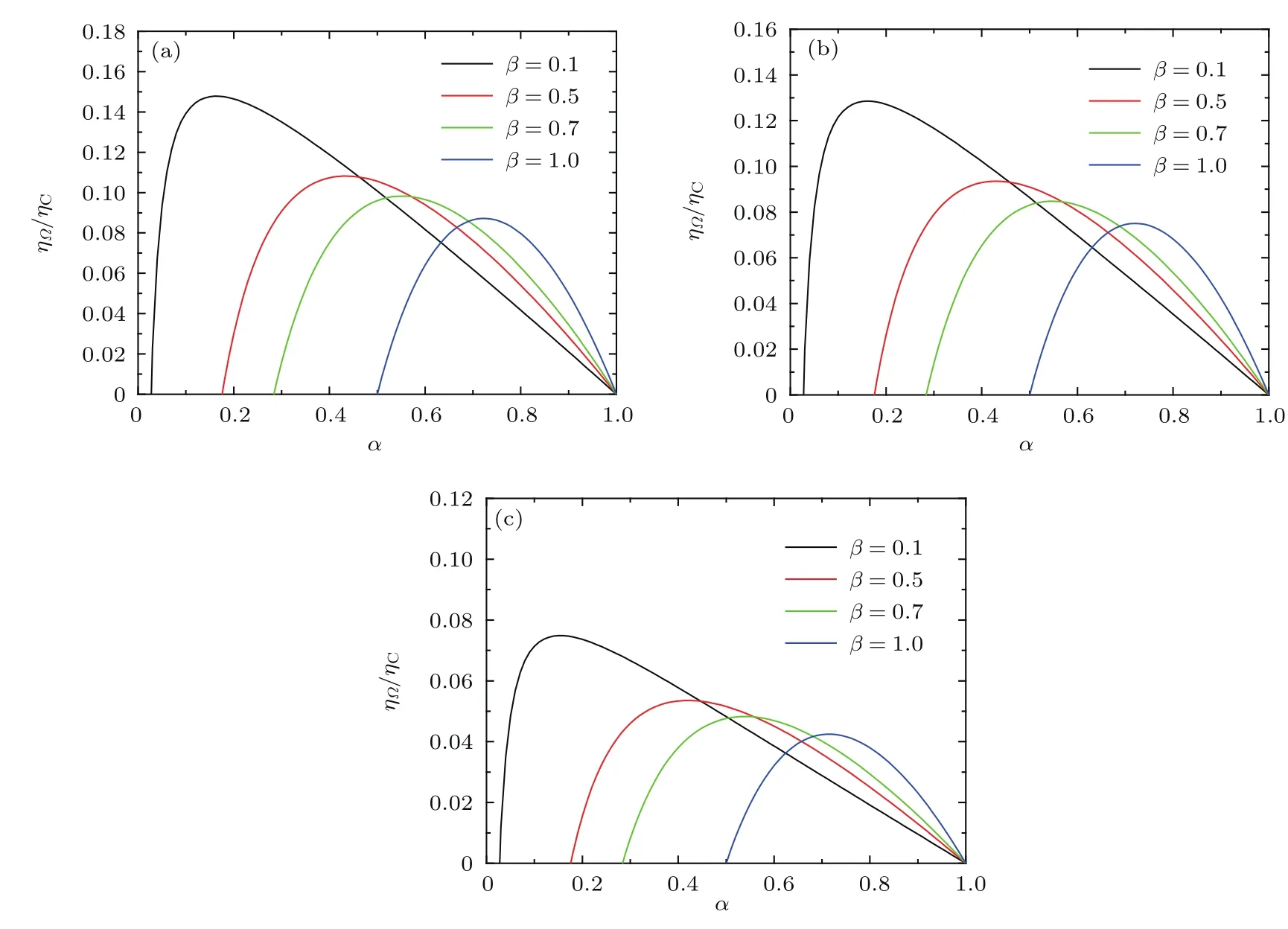
图4 (网刊彩色)当ηC=0.5和k0时,在改变β的条件下,约化效率ηΩ/ηC与α的关系 (a)n=1,m=1.25;(b)m=n=1;(c)n=4,m=1Fig.4.(color on line)ForηC=0.5 and k/0,the reduced effi ciency ηΩ/ηCvsα with the change ofβ:(a)n=1,m=1.25;(b)m=n=1;(c)n=4,m=1.

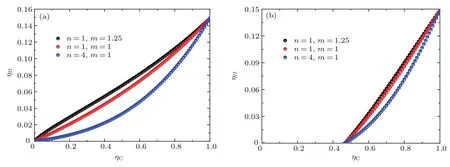
图5 (网刊彩色)(a)当α=0.3和β=0.1时,对应不同的热转移律时的热机效率ηΩ与ηC的关系;(b)当α=0.3和β=0.7时,对应不同的热转移律时的热机效率ηΩ与ηC的关系Fig.5.(color on line)(a)Forα=0.3 andβ=0.1,the effi ciency of the heat engineηΩvsηCwith diff erent heat transfer laws;(b)forα =0.3 andβ =0.7,the effi ciency of the heat engineηΩvsηCwith d iff erent heat transfer laws.

为了更好地理解权衡判据下热机效率与系统参数的关系,图5给出了不同耗散比β条件下的优化的热机效率ηΩ与卡诺效率ηC的关系曲线.发现随着ηC的增加,ηΩ呈现出单调递增的特性.但不同热转移过程支配下的热机效率特征曲线呈现出线性或者非线性行为,n的增加导致ηΩ-ηC曲线具有明显的非线性特征.在ηC较小和较大时,ηΩ的差别较小.而在中间区域,ηΩ的差异是非常明显的.另外,耗散比β增加不仅减小了热机的工作区域,而且热机效率的差异也进一步降低(如图5(b)所示).最后,图6给出了受不同热转移过程支配以及不同接触时间比条件下ηΩ与ηC的关系.ηΩ与ηC的关系也呈现出单调递增的特性.但是,当β固定不变,α增加时,热机的工作区域呈现出与图5相反的特征.进一步发现,当α较大时,热机的效率明显减小.因此,从应用角度来看,β和α的较小取值有利于热机以较大的效率进行工作.

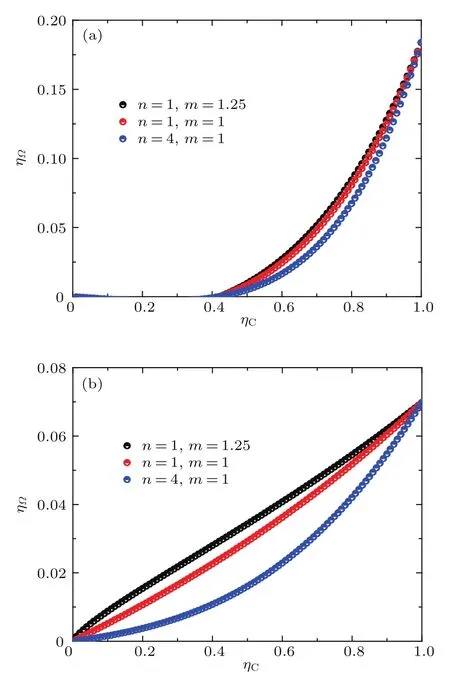
图6 (网刊彩色)(a)当β=0.3和α =0.1时,对应不同的热转移律时的热机效率ηΩ与ηC的关系;(b)当β=0.3和α=0.7时,对应不同的热转移律时的热机效率ηΩ与ηC的关系Fig.6.(color on line)(a)Forβ=0.3 andα=0.1,the effi ciency of the heat engineηΩvsηCwith d iff erent heat transfer laws;(b)forβ=0.3 andα=0.7,the effi ciency of the heat engineηΩvsηCwith d iff erent heat transfer laws.

4 结 论

本文提出了含普遍性热转移过程的低耗散热机模型,基于权衡判据原理,获得了热机的功率和效率的解析表达式.在此基础上,我们较为系统地研究了权衡判据下的热机功率及其效率.发现热机的功率以及无热转移过程的效率均不依赖于热漏项,而与接触时间、热耗散以及相应的卡诺效率有关.热机的输出功率随着卡诺效率呈现出单调递增的趋势,但是较大的接触时间比和耗散比均不利于热机在较大范围内的功率输出.在无热转移过程的热漏项且固定α(β)时,热机的效率呈现出随着β(α)的增加而减小(增加)的特征.热转移过程的出现极大地影响了热机的性能,受3种热转移规律影响的热机的ηΩ/ηC-β曲线的变化行为相似,随着α的增加,呈现出从单调减小到单调递增过度的变化特征.ηΩ/ηC-α曲线呈现出先单调增加然后单调减少的变化特征,耗散比β的增加导致了热机效率极大值的右移.另外,随着m的减小和n的增加,相应的热机效率值明显减小.受不同热转移过程支配的热机的ηΩ-ηC曲线在ηC较小或者较大时,ηΩ趋于一致,而在中间区域的差异较为明显.β较大或者α较小,热机可以正常工作的区域明显减小.本文的研究结果不仅有助于深入理解不同热转移过程支配的实际热机的优化特征,而且对设计和制造受控于不同热转移过程的热机时如何选择工作物质以及热源是有价值的.

[1]Curzon F,Ah lborn B1975Am.J.Phys.43 22

[2]van den Broeck C 2005Phys.Rev.Lett.95 190602

[3]Li J,Chen L G,Ge Y L,Sun F R 2013Acta Phys.Sin.62 130501(in Chinese)[李俊,陈林根,戈延林,孙丰瑞2013物理学报62 130501]

[4]And resen B2011Angew.Chem.In t.Ed.50 2690

[5]Hernandez AC,Medina A,RocoJ MM,W hite J A,VelascoS 2001Phys.Rev.E63 037102

[6]de Tomas C,RocoJMM,Hernandez AC,W ang Y,Tu Z C 2013Phys.Rev.E87 012105

[7]Long R,Liu Z C,Liu W 2014Phys.Rev.E89 062119

[8]Long R,Liu W 2015Phys.Rev.E91 042127

[9]Zhang Y C,Huang C K,Lin G X,Chen J C 2016Phys.Rev.E93 032152

[10]EspositoM,Kawai R,Lindenberg K,van den Broeck C 2010Phys.Rev.Lett.105 150603

[11]Izumida Y,Okuda K2012Europhys.Lett.97 10004

[12]Izumida Y,Okuda K,Hernandez AC,RocoJMM2013Europhys.Lett.101 10005

[13]Izumida Y,Okuda K,RocoJMM,Hernandez AC 2015Phys.Rev.E91 052140

PACS:05.70.Ln,05.20.–y,05.70.–aDOI:10.7498/aps.66.030504

Trade-off optimization for low-d issipation heat engine with generic heat transfer process∗

Lu Can-Can Bai Long†

(School of Physics,China University ofMining and Technology,Xuzhou 221116,China)(Received 17 August 2016;revised manuscript received 27 September 2016)

The heat transfer process inevitab ly occurs in the operation of real heat engine.In this article,a low-dissipation heat engine with generic heat transfer process is proposed based on the low-dissipation Carnot model.The formu las for the power and the effi ciency of heat engine with generic heat transfer laware derived,and the low-dissipation heat engine performance is alsooptimized by the trade-off optimization method,which off ers a unified scheme tounderstand the behaviors of heat engines with generic heat transfer processes.Furthermore,the characteristics of the power as well as the effi ciencies for thermal engines with the diff erent heat transfer processes are discussed in detail,and it is found that the power and the effi ciency without heat transfer process are independent of heat leak,but are related tocontact time,heat dissipation and Carnot effi ciency.The power output of heat enginemonotonically increases as Carnot effi ciency increases,but the large contact time ratioand the large dissipation ratiomake it diffi cult toprovide the big power output.W hen the heat leak is absent and α(β)is fixed,the effi ciency of heat engine decreases(increases)with the increase ofβ(α).It is noted that the heat transfer process greatly influences the performance of heat engine,and ηΩ/ηCversusβ displays the similar properties under three heat transfer laws.It is clearly shown thatηΩ/ηCversusβ shows the transition fromthemonotonic decrease tomonotonic increase with α increasing,butηΩ/ηCversusα is opposite tothe former,and themaximumvalue ofηΩ/ηCalsoshifts rightwards with the increase ofβ.Additionally,the corresponding effi ciency of heat engine diminishes significantly as mdecreases and n increases.W hen heat engines are dominated by diff erent heat transfer laws,the curves ofηΩversusηCare consistent asηCis relatively large or small,but it is observed that there exist the evident diff erences among three characteristic curves in the midd le regime.The relatively largeβ or smallαwill alsolead tothe reduction of the working regime where heat engine can function normally.Our results are very helpful in understanding the design principle and the optimization mechanismfor actual thermal engines and refrigerators.

low-dissipation heat engines,heat transfer laws,trade-off criterion,effi ciency of the heat engine

10.7498/aps.66.030504

∗中央高校基本科研业务费专项资金(批准号:2015XKMS082)资助的课题.

†通信作者.E-mail:bailong2200@163.com

*Project supported by the Fundamental Research Funds for the Central Universities(G rant No.2015XKMS082).

†Corresponding author.E-mail:bailong2200@163.com