边界局域模引起钨偏滤器靶板侵蚀和形貌变化的数值模拟研究∗

黄艳孙继忠桑超峰胡万鹏王德真‡

1)(大连工业大学信息科学与工程学院,大连 116034)2)(大连理工大学物理与光电工程学院,大连 116024)(2016年9月22日收到;2016年10月24日收到修改稿)

边界局域模引起钨偏滤器靶板侵蚀和形貌变化的数值模拟研究∗

黄艳1)2)孙继忠2)†桑超峰2)胡万鹏2)王德真2)‡

1)(大连工业大学信息科学与工程学院,大连 116034)2)(大连理工大学物理与光电工程学院,大连 116024)(2016年9月22日收到;2016年10月24日收到修改稿)

钨材料在高瞬时热流作用下的熔化、流动是国际热核聚变实验堆面壁材料最突出的问题.本文将热传导方程与Navier-Stokes方程结合,建立了二维流体动力学模型,研究在边界局域模(ELM)强热流轰击下,钨熔化层在表面张力、压强梯度力、磁场力等作用下的流动,以及偏滤器靶板的侵蚀和形貌演化.结果表明,在ELM过程中,熔化层中的液体不断地向边缘区域流动,在打击点区域形成一个熔池,在熔化层的边缘区域形成类似山峰结构的凸起,加重了钨偏滤器靶板的侵蚀.在空间分布为高斯形状入射能流的作用下,钨熔化层两侧的山峰结构是对称的;当能流密度小于3000 MW.m−2时,表面张力对熔化层的流动起主要作用.本文在模型的数值求解中,采用交错网格的方法进行离散,克服了液体表面追踪的算法难点,保证了钨偏滤器靶板侵蚀程度计算的准确性.

边界局域模,钨偏滤器靶板,熔化,流动

1 引 言

金属钨因为具有热导率高、熔点高、溅射率低、氚滞留率低等优点,被选作国际热核聚变实验堆(ITER)的等离子体面壁材料,但钨材料在瞬时事件,例如边界局域模(ELM)、破裂、垂直位移事件等的高热流作用下会熔化、汽化.熔化层在表面张力、磁场力、压强梯度力等作用下会流动,导致材料形貌变化,影响材料的导热能力,诱发电弧,甚至液体钨会以液滴的形式飞溅出去.这些后果不但会缩短器壁的寿命,而且产生的钨杂质(原子、尘埃、液滴)将严重威胁等离子体稳态运行[1].因此钨的熔化问题(特别是在准稳态运行时ELMs热流作用下)是以钨作为ITER面壁材料最突出的问题[2].

目前,在多个聚变实验装置(例如TEXTOR和JET)中,人们已经观察到钨偏滤器靶板的熔化以及熔化层流动的现象[3−5].但是ITER由于加热功率远高于现有聚变实验装置,并且刮削层宽度远小于现有等离子体,其等离子体与器壁相互作用的一系列问题(比如发生第一类ELMs和破裂时打到靶板的能量,全钨偏滤器靶板的侵蚀和杂质的输运等)与目前利用现有托卡马克装置外推预测的结果之间可能存在较大的差异[6],所以,理论上对该问题的分析研究就变得尤为重要.

Federici等[7−9]在一系列研究工作中建立了一维的数值求解模型,研究高热流对器壁材料的侵蚀.但其工作紧紧局限于一维研究,这样没有办法考虑能流密度空间分布的不均匀性.美国普渡大学的Hassanein等开发了HEIGHTS程序包,研究等离子体不稳定性事件中高能流对器壁材料的侵蚀[10−15].Hassanein等虽然在器壁材料侵蚀方面做了很多工作,但是对各种力作用于钨熔化层带动熔化层流动,加剧靶板侵蚀的相关问题并未开展研究.Bazylev等[16−21]建立了MEMOS模型,研究高能流对钨材料的侵蚀.但是,Bazylev等在求解模型方程过程中,先沿靶板竖直方向求解热传导方程,然后求解Navier-Stokes方程,之后再沿水平方向求解热传导方程,而实际中热传导过程在竖直和水平方向是同时进行的,所以有必要对其求解过程进一步改进.另外,对能流密度小于3000MW.m−2的情况,尚未见到考虑熔化层流动时偏滤器靶板侵蚀的详细研究.

本文在前期工作的基础上[22,23],将热传导方程和流体力学的Navier-Stokes方程结合建立了二维流体动力学模型,研究在类似ITER运行参数下发生第一类ELM过程中能流密度小于3000 MW.m−2,钨熔化层在表面张力、压强梯度力、磁场力等的作用下流动时,偏滤器靶板的侵蚀和形貌变化,详细地分析了ELM各参数对钨偏滤器靶板侵蚀程度的影响,预测未来ITER发生ELM时钨偏滤器靶板的侵蚀程度,为未来装置的设计建造提供理论依据.另外,在模型的数值求解中,对于偏滤器靶板的温度分布直接求解二维热传导方程;方程采用交错网格的方法进行离散,成功解决了液体表面追踪的算法难点,保证了钨偏滤器靶板侵蚀程度计算的准确性.

2 物理模型与数值求解

未来ITER发生第一类ELMs时打到偏滤器靶板的能量预期为1—3 MJ.m−2,沉积时间为0.1—1 ms[24,25],在此范围的能量作用下,厚度为1 cm的钨偏滤器靶板的熔化厚度为几十微米到上百微米[7,22,26],远远小于钨靶板的厚度,这属于浅水环流问题,因此可以只研究液体沿靶板表面的流动[27].如图1所示,液体流动沿x轴方向(对应着实际托卡马克装置的极向),垂直偏滤器靶板竖直向下的方向为z轴正方向.图1表示在空间分布为高斯形状能流的作用下,钨偏滤器靶板熔化,熔化层流动产生的形貌变化.模拟过程中考虑了熔化、汽化、熔化层流动和热辐射效应.

研究中考虑钨熔化层所受表面张力、压强梯度力、磁场力,忽略熔化层的重力,熔化层中的钨液体视为不可压缩液体,有

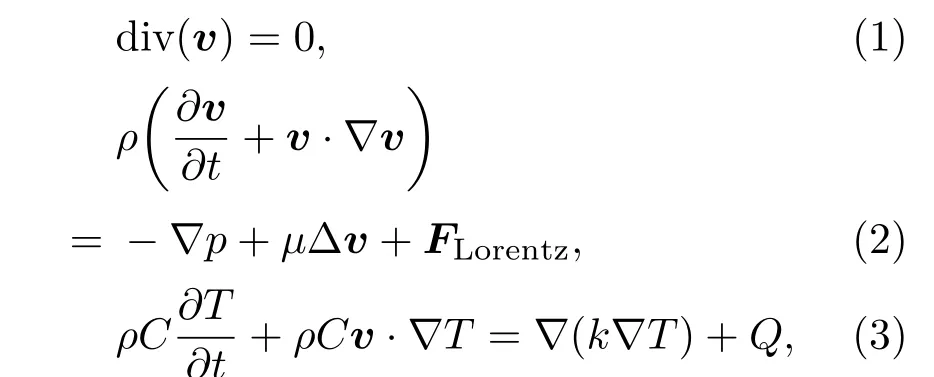
表达式中ρ,C,v,T和k分别表示钨的密度、比热、流动速度、温度和热传导系数,材料的热传导系数随温度改变,采用k=1/(aT+b)的表达形式[28],对于钨材料a=1.70× 10−6m.W−1,b=6.41×10−3m.K.W−1[29];Q是体能量沉积项;p是作用于钨液体表面的等离子体压强和蒸汽压强的总压强.

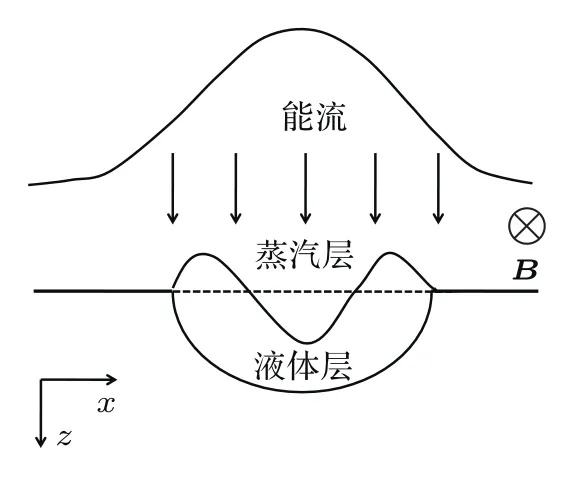
图1 熔化层及熔化层流动示意图Fig.1.Sketch of melt layer and melt motion of the target.

液体表面为自由面,表面处既要满足能量平衡条件,又要满足力平衡条件:

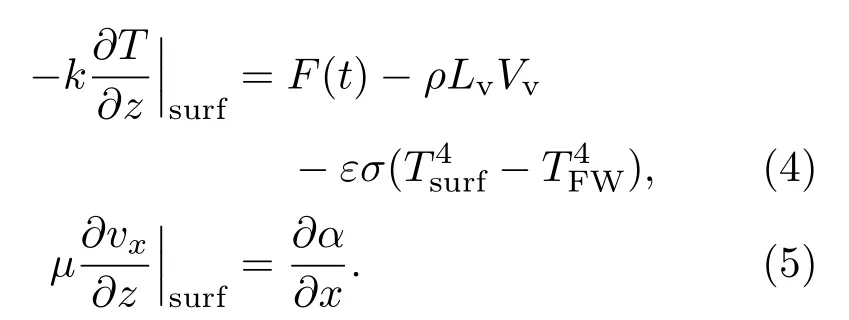
固体和液体的交界处,使用经典斯蒂芬边界条件[31]:

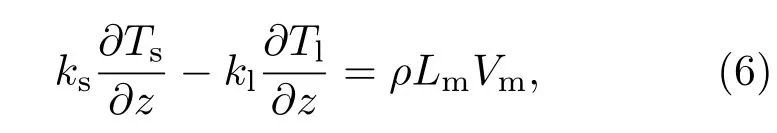
(6)式中下脚标s,l分别代表固体和液体,ks是固体部分的热传导率,kl是液体部分的热传导率,Lm表示熔化潜热,Vm表示熔化层前端的熔化速度.计算过程中,靶板底端边界条件取冷却温度350 K.

利用边界条件(5),可以将方程(1),(2)整理成描述不可压缩流体流动的一维St.Venant方程组的近似形式:

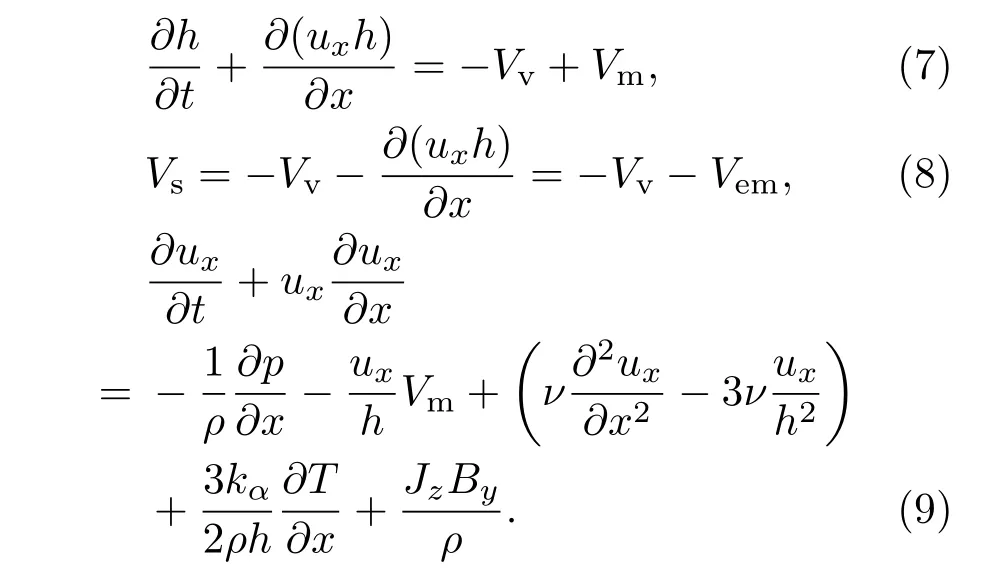
(8)和(9)式中h表示熔化层的厚度;ux表示水平方向流动速度对熔化层厚度所取的平均;ν=µ/ρ为钨液体的运动黏度;kα表示表面张力系数对温度的偏导数,是一个负值,表达式为kα=∂α/∂T;Vs表示液体表面的速度,包括两部分机制,Vv为汽化速度,Vem为由于液体流动导致熔化层厚度增加或者减少而产生的液体表面速度;Jz表示z方向的电流密度;By表示环向磁场强度(本文y轴正方向设为环向磁场的反方向).(9)式右端各项的物理意义分别为:第一项为压强梯度力,第二项表示由于液体质量增加所产生的摩擦力,第三项表示液体流动产生的黏滞力效应,第四项表示表面张力效应,第五项表示单位体积磁场力.

液体表面的汽化过程导致液体表面不断向下移动,模型中引进了运动坐标z′:

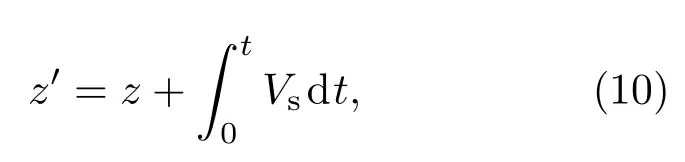
其中,z=0的位置是靶板表面的初始位置.因为发生ELMs时,极向能流密度在宽为0.1 m的范围内基本按高斯规律衰减,打击点中心的能流密度最大[32],导致作用于钨熔化层各点的压强和表面张力不同.因此本文采用二维热传导模型研究极向ELM能流不均匀导致钨熔化层在多种力作用下流动时,钨偏滤器靶板的侵蚀和形貌变化.利用运动坐标(10),热传导方程(3)可以写成如下形式:

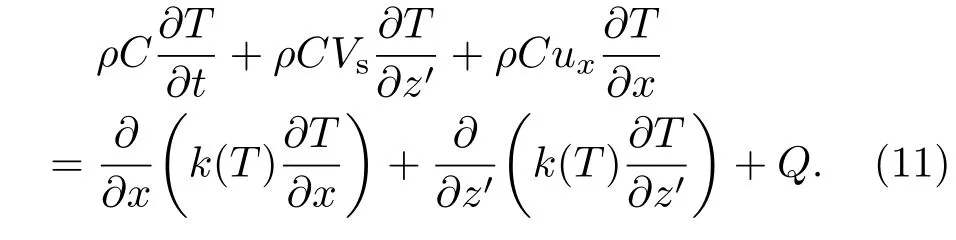
(11)式中,Vs表示钨靶板的表面速度(包括靶板表面的汽化速度以及由于液体流动导致熔化层厚度增加或者减少而产生的液体表面速度,见(8)式),ux为钨液体在水平方向的流动速度,固体部分ux为零.模拟过程中假设作用在偏滤器靶板上的极向ELM能流空间分布为高斯分布,打击点位置能流密度最大.靶板宽度取1 cm,靶板厚度取1 cm.

3 模拟结果

3.1 模型验证

为了验证物理模型的合理性,首先将本模型与已有模型进行对比.文献[17]针对钨材料和铍材料分别在电子束装置JEBIS和JUDITH中的熔化流动实验进行了模拟研究,模拟结果与实验结果非常符合,而且文献[17]中所使用的模型已经被广泛接受,因此具有一定代表性.本文针对文献[17]中空间为高斯分布的能流作用于钨靶板的例子进行了模拟,模拟参数与文献中使用的参数相同,入射能流密度的峰值为1350 MW.m−2,沉积时间为1.8ms,kα= −9.0×10−5N.m−1.K−1[17].计算结果表明,在能量沉积过程中钨靶板汽化很弱,作用于钨靶板的压强梯度力很小,不会引起钨液体流动,主要是表面张力引起钨熔化层流动,在熔化层的边缘处形成两个像山峰一样的凸起,如图2(a)所示.能流脉冲结束后靶板两端凸起的厚度约为8.35µm,文献[17]中模拟的结果也是在熔化层边缘处形成高度约为8µm的山峰,如图2(b)所示,与本文模型得到的山峰高度基本一致.

在模型的数值求解过程中,T,h和ux三个变量均采用交错网格的方法进行离散,优点是对速度分量无需再进行内插运算,同时有效地避免了常规算法处理液体流动这类问题易出现的数值噪声[33].由于本文将坐标原点设在靶板的边缘处,熔化层流动时,ELM打击点两侧的流动速度方向不同,在求解过程中分段采用上风格式,成功地追踪了熔化层流动过程中液体表面在各个时刻的位置,且所得的熔化层表面较光滑,说明本文采用的计算方法是成功的.

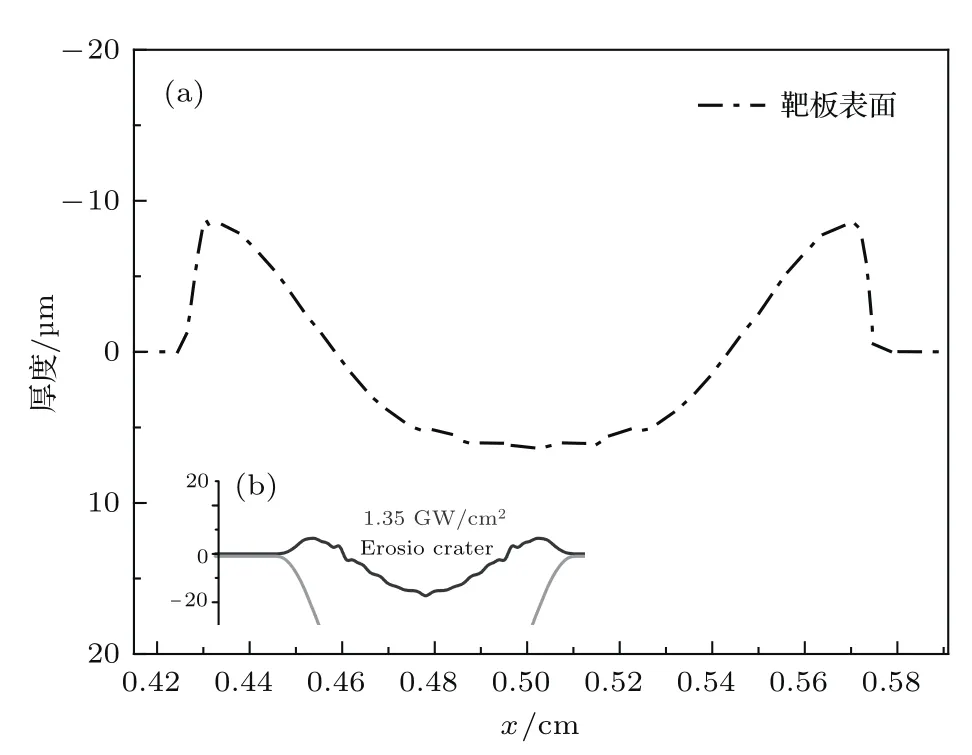
图2 钨靶板表面形貌(其中入射能流密度峰值为1350 MW.m−2,作用时间为1.8ms)(a)本文模拟结果;(b)内嵌图,文献[17]中的模拟结果Fig.2.Crater depth of tungsten under the peak power density of 1350 MW.m−2and the heat load du ration of 1.8 ms:(a)Calcu lated resu lts;(b)inset,profi le of the melt su rface in the Ref.[17].

3.2 表面形貌演化

未来ITER稳态运行时打到靶板的能流密度预期为5—20 MW.m−2[24,25],如果第一类ELMs间隙间沉积在偏滤器靶板的能流密度取10 MW.m−2,则在ELMs间隙间能流作用下,厚度为1 cm的钨靶板表面温度会达到1000 K左右[7,22]. 本文首先计算了能流密度峰值为2900 MW.m−2,持续时间为0.8 ms的ELM作用在初始温度为1000 K的钨偏滤器靶板上,考虑熔化层在表面张力和蒸汽压强梯度力(在讨论的能流密度范围内,磁场力作用远小于表面张力,所以本文忽略了磁场力)的作用下流动时,在熔化层两端形成的像山峰一样凸起的高度,偏滤器靶板的表面温度以及熔化层厚度.计算过程中kα取−9.0×10−5N.m−1.K−1[17],同时与不考虑熔化层流动时偏滤器靶板的表面温度和熔化层厚度进行了比较.

图3给出了ELM过程中3个不同时刻靶板的表面形貌.研究表明,在能量沉积过程中钨靶板汽化很弱,作用于钨靶板表面的压强梯度力很小,不能引起钨液体流动.钨靶板熔化之后,熔化层中的液体在表面张力的作用下会不断地由打击点区域向熔化层边缘区域流动,在打击点区域形成一个熔池,边缘处形成形状似山峰结构的凸起,计算时间越长,在钨液体中产生的熔池越深,边缘处形成的山峰高度越高.表1列出了从t=0.6 ms到t=0.95 ms,每过0.05 ms靶板表面凸起的最大值,也列出了该时刻与0.05 ms之前时刻熔化层凸起最大值的增加量.从表1数据可以看出,ELM能流与靶板作用时间越长,熔化层两端凸起厚度的增加速度越快.因为在本文选取的计算参数下,靶板表面的汽化量很小,靶板表面形貌变化主要由熔化层流动造成.ELM能量沉积时间越长,靶板熔化厚度越大,熔化层流动速度越大,由熔化层流动导致熔化层厚度增加或减少的幅值越大.

图3 (网刊彩色)靶板表面形貌演化,其中,能流密度峰值为2900 MW.m−2,kα取−9.0×10−5N.m−1.K−1,初始温度为1000 KFig.3.(color on line)Temporal evolution of the tungsten melt surface.Incident heat,2900 MW.m−2,kα,−9.0 × 10−5N.m−1.K−1,and initial sample temperatu re,1000 K.

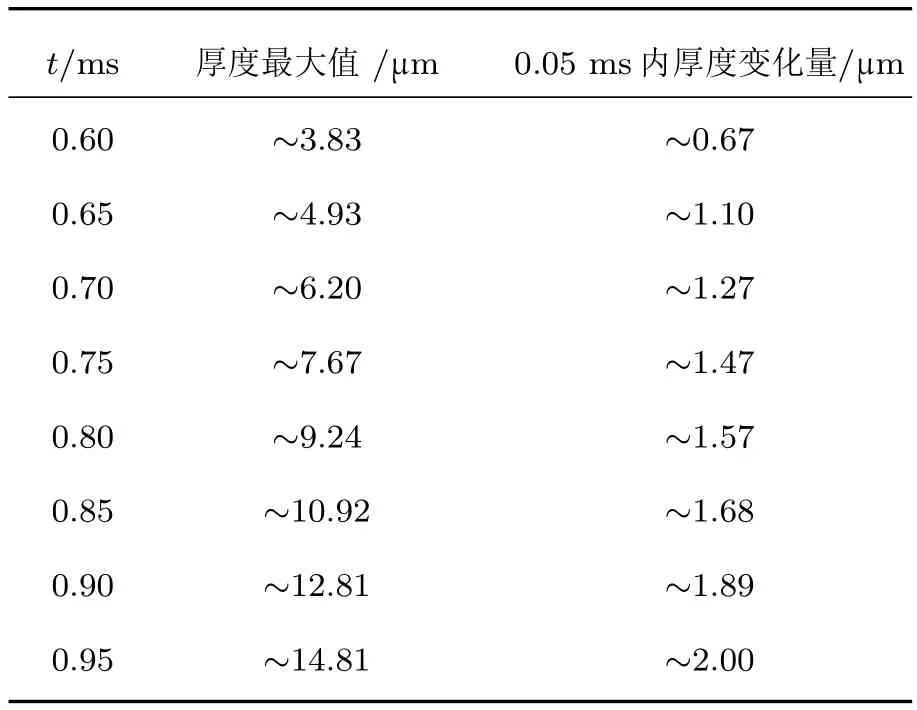
表1 各时刻熔化层两端凸起高度的最大值以及0.05 ms时间内熔化层凸起高度的变化值Tab le 1.Themaximumheight of the lumpon themelt layer edge,and increment of the lumpin 0.05 ms.

图4分别给出了考虑熔化层流动和不考虑熔化层流动,熔化区域靶板表面在三个不同时刻的温度分布.从图4可以看出,t=0.6 ms时,熔化层表面形貌变化较小,考虑熔化层流动和不考虑熔化层流动靶板表面温度相差不大.t=0.7 ms时刻,考虑熔化层流动和不考虑熔化层流动靶板表面温度开始不同.t=0.8 ms时刻,考虑熔化层流动时,x=0.46—0.54 cm之间区域靶板表面温度明显低于不考虑熔化层流动时靶板表面的温度分布,打击点处温度相差了约110 K.在x=0.39—0.46 cm之间的区域和x=0.54—0.61 cm之间的区域,考虑熔化层流动时靶板表面温度高于不考虑熔化层流动时靶板的表面温度,这是由于钨液体在流动的过程中将热量带到了熔化层的边缘区域.另外,从图4的结果还可以看出,熔化层的流动也降低了靶板表面各点的温度梯度.

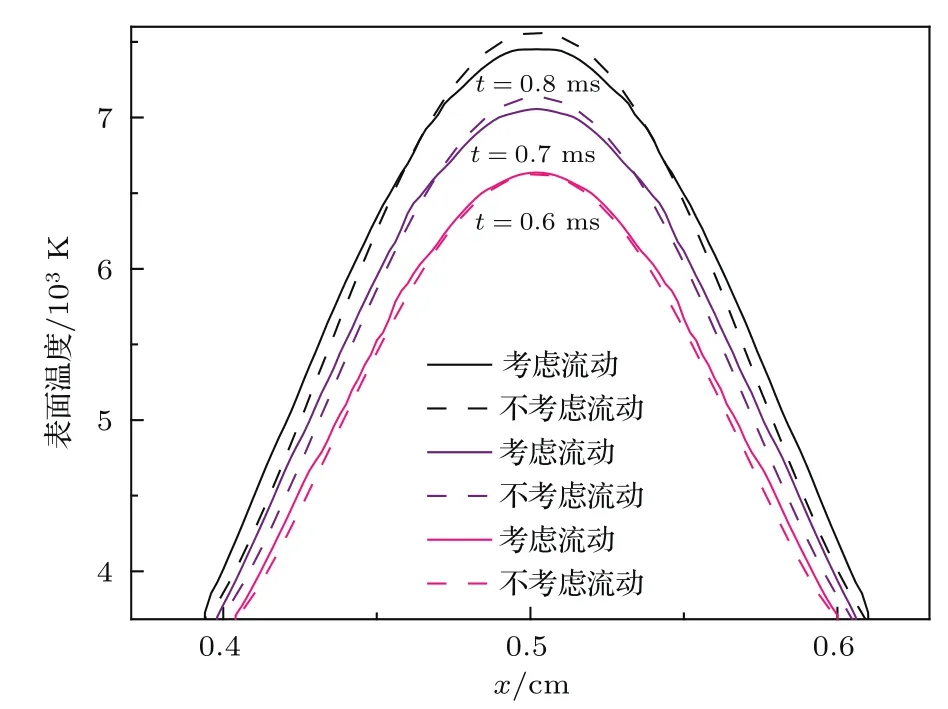
图4 (网刊彩色)偏滤器靶板的表面温度的演化,其中,能流密度峰值为2900 MW.m−2,kα取−9.0×10−5N.m−1.K−1,初始温度为1000 KFig.4.(color on line)Temporalevolu tion of the surface temperatu re with the incident heat of 2900 MW.m−2,kαof−9.0×10−5N.m−1.K−1,and the initial sample temperatu re of 1000 K.

图5分别给出了考虑熔化层流动和不考虑熔化层流动,不同时刻偏滤器靶板的熔化厚度.从图5可以看出:由于热量随着时间不断向下传导,计算时间越长,靶板的熔化厚度越大;而且,不考虑熔化层流动计算所得的熔化层前沿的位置要小于考虑熔化层流动熔化层前沿的位置,与文献[34]的规律一致,计算时间越长,二者相差越大.在t=0.6 ms,不考虑熔化层流动时,熔化层前沿位于z=77.90µm;考虑熔化层流动时,熔化层前沿位于z=79.89µm处,二者相差了约1.99µm;到t=0.7 ms时,两种情况下熔化层前沿的位置相差了约2.24µm;到t=0.8 ms时,此参数约为2.62µm.

以上结果说明,在第一类ELM热流与靶板的相互作用过程中,即使在低ELM能量作用下,作用在熔化层上的力也会导致熔化层流动,使得材料形貌发生变化,增加材料的熔化厚度.

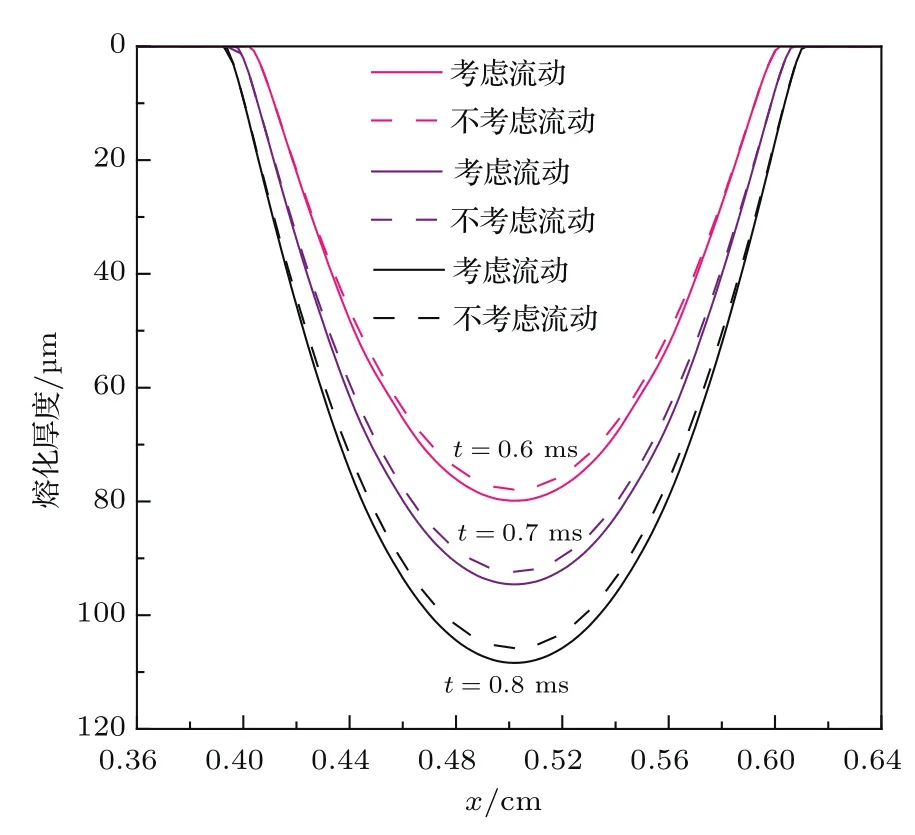
图5 (网刊彩色)靶板熔化厚度的演化,其中,能流密度峰值为2900 MW.m−2,kα取−9.0× 10−5N.m−1.K−1,初始温度为1000 KFig.5.(color on line)Temporal evolu tion of the melt front with the incident heat of 2900 MW.m−2,kαof−9.0×10−5N.m−1.K−1,and the initial sample temperatu re of 1000 K.

3.3 kα幅值的影响

靶板中杂质浓度等因素将会影响熔化层的表面张力[17],因此有必要分析不同幅值的表面张力对钨偏滤器靶板侵蚀程度的影响.图6给出了初始温度为1000 K的钨偏滤器靶板,在入射能流密度峰值为2000 MW.m−2,沉积时间为0.8ms的ELM能量作用下,表面张力系数对温度的偏导数分别取四个不同值时(kα值取自文献[17])靶板表面的形貌分布.从图6可以看出,对于kα的四个不同幅值,表面张力都引起了钨液体层流动,增加了钨靶板的侵蚀程度.kα越大,由于钨液体流动,在熔化层边缘形成的山峰高度越高.因为kα越大,钨液体的表面张力梯度越大,钨液体流动的速度越快,所以两端凸起的厚度越大.

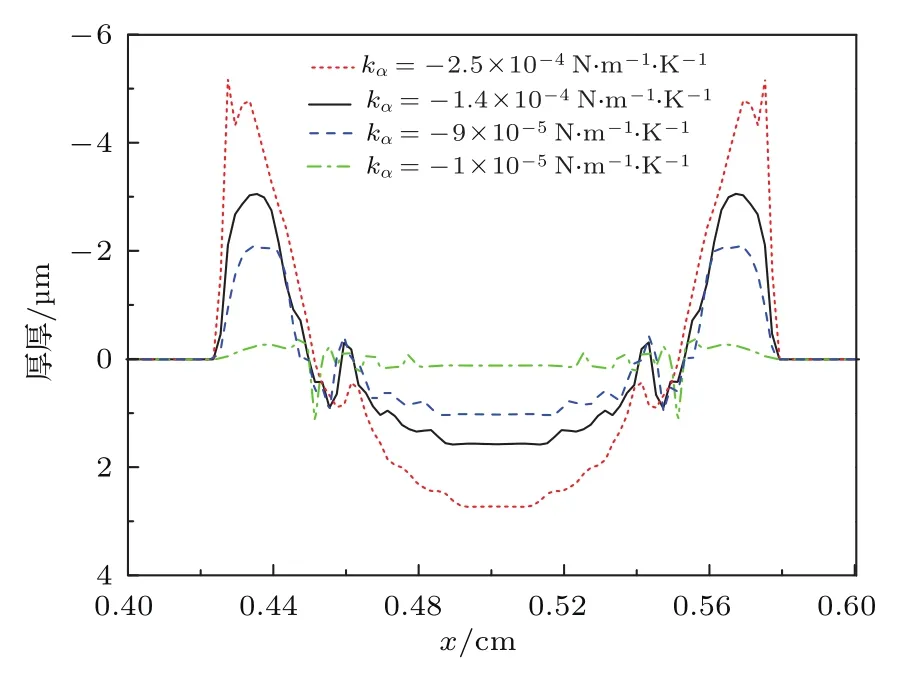
图6 (网刊彩色)靶板表面的形貌分布,其中,ELM能流密度峰值为2000 MW.m−2,沉积时间为0.8 ms,靶板初始温度为1000 KFig.6. (color on line)Calcu lated crater depth of tungsten under ELMwith a peak heat flux of 2000 MW.m−2.The heat load duration is 0.8 ms,the initial sample temperature is 1000 K.

3.4 能流密度幅值的影响

未来ITER的第一类ELMs能量范围预期为1—3 MJ.m−2,沉积时间为0.1—1 ms[24,25],本文计算了能流密度峰值分别为2000,2500,2900 MW.m−2的ELM(如图7(a)所示)作用在初始温度为1000 K的偏滤器靶板上,在持续时间为0.8 ms,kα取−9.0× 10−5N.m−1.K−1时,偏滤器靶板的表面形貌.计算结果表明:入射等离子体能流密度越大,由于钨液体流动在熔化层边缘处形成的凸起的厚度越大,这是由于入射能流密度越大,能流密度梯度越大,靶板熔化后,靶板表面温度梯度越大,在kα取相同值时,钨液体的表面张力梯度越大,钨熔化层的流动速度越快;而且,能流密度越大靶板越先熔化、流动,所以在钨熔化层两端形成的山峰高度越高.

图6和图7(b)分别说明kα和ELMs能流密度会影响靶板表面形貌.进一步分析,图6(红色虚线曲线)和图7(b)(红色点划线曲线)计算所得的熔化层两侧山峰的高度都约为5µm,两幅图的计算时间相同,靶板的初始温度相同,但图6的kα值为−2.5×10−4N.m−1.K−1,入射能流密度为2000 MW.m−2,图7(b)的kα值为−9.0×10−5N.m−1.K−1,入射能流密度为2500MW.m−2.图6的kα值约为图7(b)kα值的2.78倍,而图7(b)的能流密度仅约为图6能流密度的1.25倍.可见,由钨中杂质浓度变化等因素导致的钨熔化层表面张力改变对靶板表面形貌的演化只起次要作用,而ELMs本身的特征参数变化对靶板表面形貌的改变起主要作用.

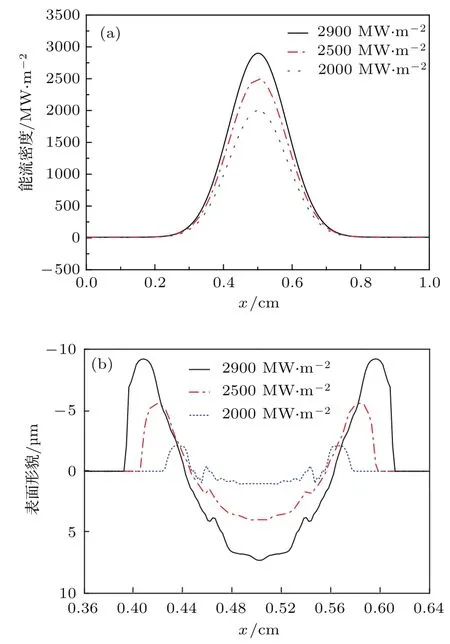
图7 (网刊彩色)能流密度峰值分别为2000,2500和2900 MW.m−2时的(a)能流密度分布曲线和(b)偏滤器靶板表面形貌;ELM沉积时间为0.8 ms,kα为−9.0×10−5N.m−1.K−1,靶板初始温度为1000 KFig.7. (color on line)(a)Incident heat loads and(b)temporal evolution of the tungsten melt surface calculated with peak heat fl uxes of 2000,2500 and 2900 MW.m−2.The heat load duration is 0.8 ms,kαis−9.0×10−5N.m−1.K−1,and the initial sample temperatu re is 1000 K.

3.5 讨 论

为了更好地分析不同物理量对钨偏滤器靶板侵蚀程度的影响,本文进一步比较了各种参数下偏滤器靶板的粗糙度,粗糙度定义采用(12)式的形式[35,36]:

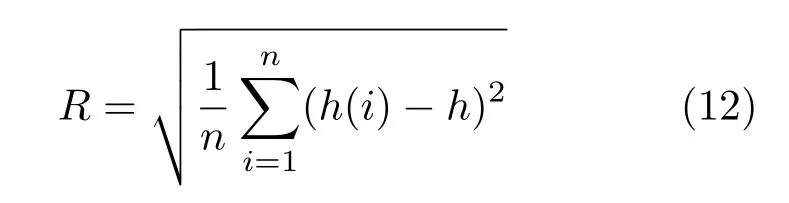
(12)式中h(i)表示偏滤器靶板表面每点的高度,h表示偏滤器靶板表面的平均水平高度.图8(a)—(c)分别给出了偏滤器靶板表面粗糙度随入射能流密度、kα值和ELM持续时间的变化.图8(a)的计算结果表明,ELM的持续时间为0.8ms,入射能流密度约为1650MW.m−2时,靶板表面粗糙度约为零.因为此时靶板刚开始熔化,钨液体在熔化层两侧形成的山峰状凸起非常小,约为10−4µm.随着入射能流密度的增加,靶板表面粗糙度线性增加.图8(b)和图8(c)的结果表明,偏滤器靶板表面的粗糙度分别与液体表面张力系数对温度的偏导数kα和ELM持续时间成正比.kα越大,ELM作用时间越长,钨熔化层流动导致熔化层边缘处山峰的高度越高,偏滤器靶板表面形貌变化越大.

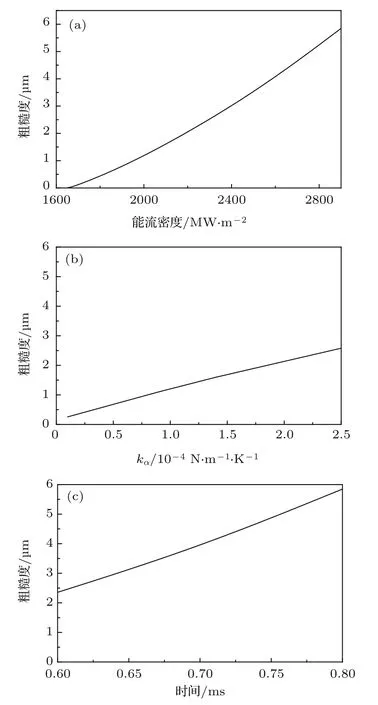
图8 钨偏滤器靶板表面粗糙度与(a)入射能流密度、(b)kα值和(c)ELM持续时间的关系Fig.8.Surface roughnessvarieswith(a)incident heat,(b)kαand(c)ELMdu ration.

4 结 论

本文通过将热传导方程与Navier-Stokes方程结合,建立了二维流体动力学模型,分别从ELM本身参数和靶板角度,详细地研究了在类似ITER运行参数下发生第一类ELM过程中,偏滤器靶板的侵蚀和形貌演化,得到如下结论.

1)ELM能流与靶板相互作用的过程中,钨熔化层会发生流动,作用时间为0.8 ms,kα为−9.0 × 10−5N.m−1.K−1, 入射能流密度 大于2000 MW.m−2时,偏滤器靶板表面形貌发生明显变化.入射能流密度若为2000 MW.m−2,靶板表面粗糙度约为1.1µm,熔化层两端凸起的厚度约为2.1µm;入射能流密度若为2500 MW.m−2,靶板表面粗糙度约为3.4µm,熔化层两端凸起的厚度约为5.4µm;入射能流密度若为2900 MW.m−2,靶板表面粗糙度约为5.8µm,熔化层两端凸起的厚度约为8.4µm.ELM持续时间越长,熔化层两端凸起厚度的增加速度越快;考虑熔化层流动时,熔化层边缘区域的温度高于不考虑熔化层流动时的温度,中心区域温度相对降低,熔化层厚度相对增加.

2)当入射能流密度相同时,表面张力系数对温度的偏导数kα越大,表面张力梯度越大,偏滤器靶板表面形貌变化越大.当表面张力系数对温度的偏导数kα相同时,入射能流密度越大,偏滤器靶板表面温度梯度越大,偏滤器靶板形貌变化越大.

ITER每次放电过程中,发生第一类ELMs的次数不少于103[32],偏滤器靶板表面形貌会发生显著变化,这将严重影响材料的性能,甚至诱发电弧.下一步工作,我们将研究在多个ELMs热流作用下偏滤器靶板的侵蚀.

[1]Xu W,Wan BN,Xie J K2003Acta Phys.Sin.52 1970(in Chinese)[徐伟,万宝年,谢纪康 2003物理学报 52 1970]

[2]Coenen J W,Arnoux G,Bazy lev B,Matthews G F,Autricque A,Balboa I,C lever M,Dejarnac R,Coff ey I,Corre Y,Devaux S,Frassinetti L,Gau thier E,Horacek J,Jachmich S,KommM,KnaupM,Krieger K,Marsen S,Meigs A,Mertens P,Pitts R A,Puetterich T,Rack M,StampM,SergienkoG,Tamain P,Thompson V,JET-EFDAContributors 2015Nucl.Fusion55 023010

[3]SergienkoG,Bazy lev B,Huber A,Kreter A,Litnovsky A,Rubel M,Philipps V,Pospieszczyk A,Mertens P,SammU,Schweer B,Schmitz O,Tokar M,The TEXTOR Team2007J.Nucl.Mater.363 96

[4]SergienkoG,Bazylev B,Hirai T2007Phy.Scr.T128 81

[5]Coenen J W,Arnoux G,Bazy lev B,Matthews G F,Jachmich S,Balboa I,C lever M,Dejarnac R,Coff ey I,Corre Y,Devaux S,Frassinetti L,Gau thier E,Horacek J,KnaupM,KommM,Krieger K,Marsen S,Meigs A,Mertens Ph,Pitts R A,Puetterich T,Rack M,StampM,SergienkoG,Tamain P,Thompson V,JET-EFDAContributors 2015J.Nucl.Mater.463 78

[6]Federici G,And rewP,Barabaschi P,Brooks J,Doerner R,Geier A,Herrmann A,Janeschitz G,Krieger K,Kukushkin A,Loarte A,Neu R,Saibene G,Shimada M,Strohmayer G,Sugihara M2003J.Nucl.Mater.313 11

[7]FedericiG,Loarte A,Strohmayer G 2003P lasma Phys.Con trol.Fusion45 1523

[8]Raff ray AR,Federici G 1997J.Nucl.Mater.244 85

[9]Federici G,Raff ray AR 1997J.Nucl.Mater.244 101

[10]Hassanein A,Konkashbaev I2000Fusion Eng.Des.51 681

[11]Sizyuk V,Hassanein A2015Phy.Plasmas22 013301

[12]Litunovsky V N,Kuznetsov V E,Lyub lin BV,Ovchinnikov IB,Titov V A,Hassanein A2000Fusion Eng.Des.49 249

[13]Shi Y,Miloshevsky G,Hassanein A2011Fusion Eng.Des.86 155

[14]Hassanein A,Konkashbaev I2003J.Nucl.Mater.313 664

[15]GencoF,Hassanein A2014Laser Part.Beams32 217

[16]W urz H,Bazy lev B,Landman I,Pestchanyi S,G ross S 2001Fusion Eng.Des.56 397

[17]Bazylev B,Wuerz H2002J.Nucl.Mater.307 69

[18]Coenen J W,Bazylev B,Brezinsek S 2011J.Nucl.Mater.415 S78

[19]Bazylev BN,Janeschitz G,Landman IS,Pestchanyi S E 2005Fusion Eng.Des.75 407

[20]Bazylev BN,Janeschitz G,Landman IS,Loarte A,Pestchanyi S E 2007J.Nucl.Mater.363 1011

[21]Igitkhanov Y,Bazy lev B2014IEEE Trans.P lasma Sci.42 2284

[22]Huang Y,Sun J Z,Sang C F,D ing F,W ang D Z 2014Acta Phys.Sin.63 035204(in Chinese)[黄艳,孙继忠,桑超峰,丁芳,王德真2014物理学报63 035204]

[23]Huang Y,Sun J Z,Hu W P,Sang C F,W ang D Z 2016Fusion Eng.Des.102 28

[24]Miloshevsky G V,Hassanein 2010Nucl.Fusion50 115005

[25]Loarte A2003P lasma Phys.Con trol.Fusion45 1549

[26]Hassanein A,Sizyuk T,Konkashbaev I2009J.Nucl.Mater.390 777

[27]Jiang C B,Zhang Y L,Ding Z P 2007Computational F luid Mechanics(the fi rst edition)(Beijing: China Power Press)p211(in Chinese)[江春波,张永良,丁则平2007计算流体力学(第一版)(北京:中国电力出版社)第211页]

[28]CarslawHW,Jaeger J C 1959Conduction of Heat in Solids(2nd Ed.)(Ox ford:C larendon Press)pp89–91

[29]Beh risch R 2010J.Synch.Investig.4 549

[30]Semak V V,Damk roger B,Kempka S 1999J.Phys.D:Appl.Phys.32 1819

[31]Udaykumar HS,Shyy W 1995In t.J.Heat Mass Transfer38 2057

[32]Bazylev BN,Janeschitz G,Landman IS,Pestchanyi S E 2005J.Nucl.Mater.337 766

[33]Udaykumar HS,Shyy W,RaoMM1996In t.J.Numer.Methods Fluids22 691

[34]W urz H,Pestchanyi S,Bazy lev B,Landman I,Kappler F 2001J.Nucl.Mater.290 1138

[35]E lsholz F,Scholl E,Scharfenorth C,Seewald G,Eich ler HJ,Rosen feld A2005J.Appl.Phys.98 103516

[36]E lsholz F,Scholl E,Rosen feld A2004Appl.Phys.Lett.84 4167

PACS:52.55.Fa,52.55.Rk,52.40.Hf,52.65.KjDOI:10.7498/aps.66.035201

N umerical study of thermal erosion and topograph ical change of d ivertor target plates induced by type-Iedge-localized modes∗

Huang Yan1)2)Sun Ji-Zhong2)†Sang Chao-Feng2)Hu Wan-Peng2)Wang De-Zhen2)‡

1)(School of Information Science and Engineering,Dalian Polytechnic University,Dalian 116034,China)2)(School of Physics and Optoelectronic Engineering,Dalian University of Technology,Dalian 116024,China)(Received 22 September 2016;revised manuscript received 24 October 2016)

The high-Z material tungsten(W)is a promising candidate of the plasma facing components(PFCs)for the future tokamak reactors due toits high melting point(3683 K),lowtritiumretention and lowsputtering yield.However,there are stillmany problems aboutW PFCs.One of themis thematerialmelting under off-normal transient heat fluxes—it is one of themost outstanding open questions associated with the use ofW divertor targets in international thermonuclear experimental reactor(ITER).This requires us urgently tounderstand the W melting behavior under high power flux deposition condition.In this paper,a two-dimensional(2D)fl uid dynamic model is employed by solving the liquid hydrodynamic Navier-Stokes equation together with the 2D heat conduction equation for studying the erosion of the divertor tungsten targets and its resu lting topographicalmodification during a type I-like edge-localized mode(ELM)in ITER with a Gaussian power density profi le heat load.In the present model,major interaction forces,including surface tension,pressure gradient and magnetic force responsible for melt layer motion,are taken intoaccount.The simulation results are fi rst benchmarked with the calcu lated resu lts by other code tovalidate the presentmodeland code.Simulations are carried out in a wide range of fusion plasma performance parameters,and the results indicate that the lifetime ofW plate is determined mainly by the evolution of themelt layer.As a consequence of themelt layermotion,melted tungsten is flushed tothe periphery,a rather deeperosion dent appears,and at the dent edges twohumps of tungsten formduring the ELM.The humps at both edges are almost at the same height.Calculated results showthe topographicalmodification becomes noticeab le when the W plate is exposed toa heat flux of 2000 MW.m−2for 0.8 ms(in the simu lation,the parameter kα= ∂α/∂Tis taken tobe −9.0× 10−5N.m−1.K−1,where α is the surface tension coeffi cient and Tis the temperature).The values of the humps are both about 2.1µm,and the surface roughness is about 1.1µm.The longer the duration of the ELM,the more rapid ly the humps rise.Themelt flowmay account for the higher surface temperature at the pool periphery,and for the largermelt thickness.It is found that when the energy flux is under 3000 MW.m−2the surface tension is a major driving force for themotion ofmelt layer.Under the same heat flux,the bigger the kαused in the simu lation,themore severe the surface topography of the target becomes;while at the same kα,the higher the heat flux,themore severe the surface topography of the target becomes.In addition,a modified numericalmethod algorithmfor solving the governing equations is proposed.

edge-localized modes,tungsten divertor plate,melting,flowing

10.7498/aps.66.035201

∗国家磁约束聚变科学项目(批准号:2013GB109001,2013GB107003)、国家自然科学基金(批准号:11275042,11575039)和辽宁省基本科研项目(批准号:2016J027)资助的课题.

†通信作者.E-mail:jsun@d lu t.edu.cn

‡通信作者.E-mail:wangdez@d lu t.edu.cn

*Project supported by the National Magnetic Con finement Fusion Science Programof China(G rant Nos.2013GB109001,2013GB107003),the National Natural Science Foundation of China(G rant Nos.11275042,11575039),and the Scientifi c Research Foundation of the Liaoning Province,China(G rant No.2016J027).

†Corresponding author.E-mail:jsun@d lut.edu.cn

‡Corresponding au thor.E-mail:wangdez@d lut.edu.cn