基于压缩感知的窄带高速自旋目标超分辨成像物理机理分析∗

李少东陈永彬 刘润华 马晓岩

(空军预警学院三系,武汉 430019)(2016年5月13日收到;2016年8月25日收到修改稿)

基于压缩感知的窄带高速自旋目标超分辨成像物理机理分析∗

李少东†陈永彬 刘润华 马晓岩

(空军预警学院三系,武汉 430019)(2016年5月13日收到;2016年8月25日收到修改稿)

常规窄带雷达系统对高速自旋的空天目标成像时,方位脉冲重复频率通常难以满足采样率要求.而基于压缩感知(compressive sensing,CS)理论则可实现欠采样条件下窄带高速自旋目标的成像.本文对这一成像的物理机理进行分析和讨论.首先,构建方位欠采样回波模型,分析了该模型与CS理论的关系;其次,从物理角度分析基于CS理论可以保证欠采样条件下散射点准确重构的机理,给出欠采样倍数的理论下限值.仿真结果表明,欠采样条件下窄带雷达系统可实现对高速自旋目标二维成像,同时验证了基于CS的欠采样成像性能与欠采样倍数、等效强散射点个数以及波长等有关,与信号带宽无关等结论.

欠采样,压缩感知,高速自旋目标,超分辨

1 引 言

对空间碎片、自旋弹头、空中旋翼飞机等具有高速自旋特性的空天目标进行准确的参数估计和成像[1],对于目标识别、防空预警等领域具有重要的应用价值.然而,对于高速自旋目标而言,常规雷达很难满足方位采样率的需求,这将导致方位向欠采样,出现多普勒模糊,因此立足于常规雷达系统实现空天自旋目标超分辨成像具有重要的研究价值.

为解决对高速自旋目标成像时的这一难题,众多学者展开了相关的研究.根据研究的侧重点可大致分为两类.一是方位满足采样条件下的成像方法研究.文献[2]采用双基地雷达利用文献[3]提出的单距离单元多普勒干涉法(single range Doppler interferometry,SRDI)进行自旋目标成像,但是SRDI受限于时频分析的分辨率或交叉项等固有问题,适用范围有限;文献[4]研究了复数后向投影(back projection,BP)算法进行成像;文献[5]提出了基于实数逆Radon变换(realvalued inverse Radon transform,RIRT)和复数逆Radon变换(complex-valued inverse Radon transform,CIRT)的旋转部件二维成像方法.这一类方法的共同特征是要求方位采样率大于回波的最大多普勒带宽,否则将产生虚假重构散射点,这对于高速自旋目标而言是很难满足的.第二类方法是在欠采样条件下的成像方法.文献[4]依据压缩感知(compressive sensing,CS)理论进行欠采样条件下的自旋目标成像方法,获得了良好的成像效果;文献[6]则使用精度更高的压缩采样匹配追踪(compressive sampling matching pursuit,CoSaMP)算法成像,但是该方法的效率有所降低;文献[7]提出了一种对空间碎片群的成像方法,但是并未讨论自旋频率未知时如何成像的问题.这一类方法的共同特征是要求用于成像的自旋目标的角速度已知,并未从物理意义的角度讨论欠采样条件下可超分辨成像的机理.总结目前的研究现状可知,虽然对欠采样条件下的自旋目标成像方法已有一些研究,但是并未对CS的欠采样成像机理等问题进行探讨.

本文在已有的CS窄带成像方法基础上,研究基于CS理论的自旋目标欠采样成像的物理机理.首先构建自旋目标的欠采样回波模型,明确该模型与CS理论的关系;其次,从物理角度解释为何基于CS理论可以保证欠采样条件下散射点的准确重构,然后给出欠采样倍数的理论下限值,并给出超分辨倍数的上限.本文研究可为高速自旋空天目标的欠采样成像提供物理依据.

2 自旋目标窄带雷达成像回波模型

通常而言,雷达对目标成像主要是利用大带宽获得距离维高分辨,利用多普勒处理技术来实现方位高分辨.而窄带雷达由于带宽的约束,一般仅能获取目标的距离、方位等信息,难以获得目标的高分辨二维图像.但是对于空间碎片等高速自旋目标而言,若在观测时间内目标的转角足够大,则有可能在距离分辨率较低的条件下,对单个距离单元回波采用信号处理的手段得到其二维图像.本文充分利用高速自旋目标的运动特征,探讨在窄带欠采样条件下基于CS理论可获取目标二维超分辨图像的物理机理.首先建立空间碎片等高速自旋目标的欠采样回波模型,并进一步分析该模型与CS理论的关系.

为便于分析,本文假设在观测时间内平动补偿已完成,目标绕自身旋转中心做恒定角速度的高速自旋运动,如图1所示.在光学区,目标的散射场主要由强散射中心构成.假设自旋目标可等效为K个强散射点,其在目标坐标系中的初始位置为(xk,yk),通常自旋目标的旋转频率很高,为避免多普勒模糊,需要很高的脉冲重复频率(pulse repetition frequency,PRF).然而常规雷达的PRF一般无法满足这一需求,将出现方位欠采样的情况.此外,当部分脉冲受到干扰或遮挡时需要人为剔除部分脉冲,将造成成像数据不完整,出现方位随机欠采样的情况.本文将均匀欠采样和随机欠采样统称为方位欠采样.首先构建欠采样回波模型.

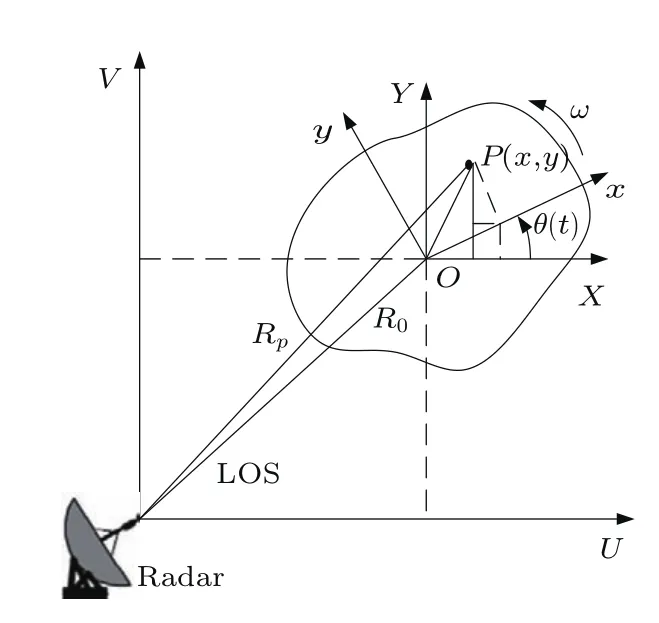
图1 自旋目标与雷达关系示意图Fig.1.Geometry of the radar and the spinning target.

假设雷达发射线性调频(linear frequency modulation,LFM)信号,远场目标上某一散射点P至雷达的瞬时斜距可近似为

其中,R0为目标自旋中心到雷达的距离,(rp,φp)为P点在目标坐标系中的初始位置和角度,ω为目标角速度,tm为慢时间.假设共有K个强散射点,对目标回波进行Dechirp以及补偿剩余相位视频项(RVP)处理后有[8]

其中fk为第k个散射点的快时间频率,R∆=Rp− Rref=rpsin(ωtm+ φp),Tp为脉冲宽度,λ为波长,γ为调频斜率,˜σk为散射点的后向散射场幅度,n(tf,tm)为复高斯噪声.由(2)式及R∆表达式可知,与逆合成孔径雷达成像时目标回波表达式不同,高速自旋目标强散射点的包络和相位在距离-转角域是按正弦规律变化的,且不再满足Taylor级数的一阶近似展开条件(即sin(ωtm)/= ωtm).而利用此正弦规律可在窄带条件下获得高分辨的二维图像,如RIRT算法利用包络的正弦变化进行成像[5];CIRT算法利用旋转散射点的正弦相位沿慢时间进行相干积累来获得二维图像[5].但是这两种方法只在非欠采样条件下效果较好.本文主要考虑利用散射点在方位向的相位信息来进行超分辨成像.由于直径是几厘米或几十厘米的空间碎片,即使带宽为100 MHz左右时目标散射点散射幅度最强的位置也将集中于一个距离单元,因此可在距离向Dechirp后幅度最大的回波所在距离单元,此时回波表达形式为

式中,R∆=rpsin(ωtm+ φp)=xksin(ωtm)+ykcos(ωtm).本文的目的是从回波s(tm)中准确地反演出强散射点的幅度和位置信息.因此,可将目标等效为一组位于二维场景网格上的散射点.场景图像离散化后在距离向共有M个像素单元,在方位向上共有N个像素单元,构成的二维图像为X∈CM×N.由于目标的等效强散射点共有K个,实际中K≪M×N,满足稀疏性条件.为便于描述,首先给出方位满足采样条件时的回波稀疏表示模型.

由(3)式可以看出,回波s(tm)与三个变量有关,即慢时间tm、距离向位置yi和方位向位置xi.因此首先对场景进行向量化处理,即令x=vec(X)=[σ1,...,σ2,...,σK,...]MN×1;用t表示方位慢时间序列,t=(0:Na)/PRF,其中Na为满采样的方位脉冲数.此时回波可稀疏表示为

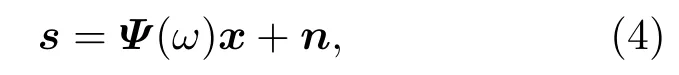
其中,s为方位向采样序列;Ψ(ω)∈CNa×MN为含参数的稀疏基,第i列为

⊗为Kronecker积.Ψ(ω)的计算与角速度ω有关,目前已有众多学者进行了角速度估计的相关研究,大致可分为两类.一类是相关法[9],这一类角速度估计的方法受到PRF的限制,估计的角速度范围有限;二是利用图像熵估计角速度[10],这一类方法不受PRF制约,估计性能较好.本文假设角速度已准确估计.

文献[11]指出,为避免方位向出现虚假重构散射点,雷达系统的PRF应满足:

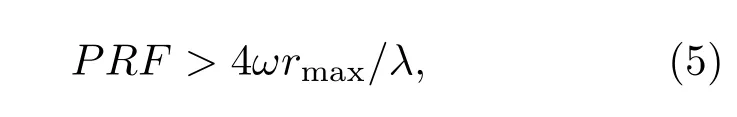
其中rmax为目标最大的旋转半径.在实际情况下,高速自旋的目标将产生方位欠采样回波.令Na表示非欠采样时的脉冲数,假设欠采样倍数为δ,那么实际接收到的回波脉冲数应为此时可将方位降采样等效为(4)式乘以欠采样矩阵那么欠采样回波可表示为

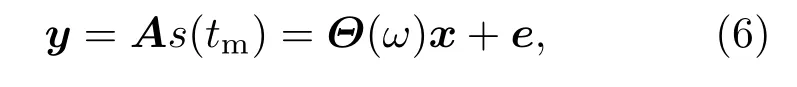
其中Θ(ω)为感知矩阵,(6)式即为欠采样条件下的回波模型.此外若方位回波随机缺损时,可等效认为A的某些行置零.

由(6)式的构建过程可知,其利用了自旋目标强散射点个数是稀疏的这一特征,将方位欠采样过程等效为一个欠采样矩阵,而这一过程恰好与CS理论相符合.因此可以认为(6)式是一个基本的CS数学表示模型.文献[4,6]分别使用正交匹配追踪(OMP)和CoSaMP来重构(6)式,获得了较好的成像效果.但是并没有就为何在欠采样条件下可以窄带高分辨成像的物理机理进行研究,下面本文重点对此问题进行分析.

3 基于CS理论的自旋目标欠采样成像机理分析

首先从物理角度分析为何基于CS理论可以保证欠采样条件下散射点的准确重构,然后给出欠采样倍数的理论下限值.

将(3)式中第k个散射点的相位对慢时间求导可得到

其中fDk为第k个散射点的多普勒频率.(7)式表明,每一个散射点的多普勒信息与散射点的位置、波长和目标自旋角速度有关.由于不同散射点的位置不同,因此其多普勒频率也不相同,利用不同散射点在方位多普勒上的差异性进行方位分辨就是窄带条件下高速自旋目标可成像的本质.但是(7)式同时也揭示了另一问题:散射点的多普勒具有周期性,若想通过直接计算多普勒来区分不同散射点难度较大,因为必须保证方位向采样速率满足(5)式,才能不混叠.而CS重构时则巧妙地避开了直接计算多普勒,在利用不同散射点的多普勒差异性的同时,通过直接寻找散射点“位置”信息的方式,获得高分辨成像质量.这种从估计散射点多普勒频率到散射点位置的变化使得即使方位多普勒存在模糊,也可实现高速自旋目标成像,这就是基于CS可实现欠采样条件下的超分辨成像的原因.

上述分析表明,基于CS进行欠采样成像的关键在于重构过程中散射点位置能否被正确地找到.以OMP重构为例说明这一问题.假设目标可等效为K个强散射点,OMP算法通过迭代寻找散射点支撑集位置后,使用最小二乘估计恢复其散射系数.令Rj−1表示第j−1次迭代的残差,G(j)=ΘHRj−1,G(j)为第j次迭代时感知矩阵与残差内积.Θ的第i个原子与量测y的内积为

由(8)式 可知,当∆xki= 0,∆yki= 0,|〈Θi,y〉|为最大值,对应的原子Θi即是真实散射点所在的位置.但是由于指数函数的周期性,当下式成立时,

其中k为整数,(8)式相位项将变为exp(j2kπ),也有|〈Θj,y〉|=Na,此时将出现虚假重构点.但是实际上(9)式成立的概率很小.现推导其成立时∆xki,∆yki需要满足的条件.对(9)式两端同时除以∆xkicos(ωtm),有

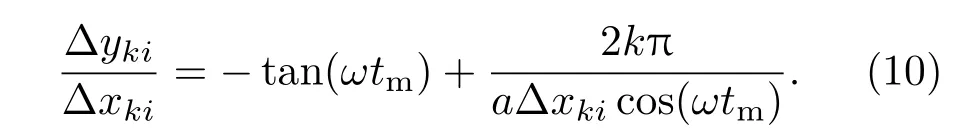
若划分网格时选择整数网格点,即令∆y/∆x为整数,则(10)式右半部分的值一般无法保证在每一个慢时间的时刻都取到整数,即(10)式成立的概率很小,从而在∆xj/0,∆yj/0的位置,有|〈Θi,y〉|＜ Na,无法保证最大值.

进一步对(8)式中的正弦和余弦函数用贝塞尔函数展开后,(8)式转换为

Jl(Z)是指第l阶贝塞尔函数.现结合(11)式分析强散射点位置能否被准确找到.

图2 Jl(zki)的贝塞尔函数 (a)l=0;(b)l=1;(c)l=10;(d)l=100Fig.2.Bessel functions of Jl(zki):(a)l=0;(b)l=1;(c)l=10;(d)l=100.

由于OMP重构时是通过寻找与量测值内积最大的列进行的,因此使得|〈Θi,y〉|最大的列的位置即为某个强散射点所对应的位置.根据贝塞尔函数性质,当l很大时,Jl(zki)将变得很小.图2为l取0,1,10,100,zki/λ取[−1,+1]时Jl(zki)的函数图形.

由图2以及贝塞尔函数的性质可知,随着阶数l的增加,Jl(Z)的取值不断减少,且会收敛(收敛速度很快,当l=10时,在中间部分几乎取值为0),(11)式中|〈Θi,y〉|的内积的值主要是由第一项来决定.因此当i=k时,zki=0,有

(12)式成立的原因是J0(0)=1.可见对于第k个散射点,有

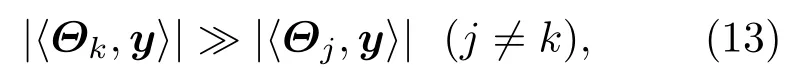
此时能保证原子的位置被准确找到.因此(13)式即是散射点能否被准确找到的约束条件,由于OMP算法每次只选择一个幅度最强的散射点,且通过迭代更新残差,因此还可以避免散射点之间的相互干扰与旁瓣影响.

实际上,由于网格失配的存在[12],zki不一定等于0,而是一个趋近于0的数.由J0(zki)的图形可知,其第1零点宽度为0.4λ.因此当zki/0时,应保证J0(zki)的值尽可能的大,即保证在J0(zki)的第1零点宽度内采集到值,这样才能保证(13)式以很大的概率成立.因此对于欠采样窄带成像问题,网格失配误差应控制在0.4λ以内,否则会引起错误重构.

此外,两个散射点之间的最小间隔也应大于0.4λ,只有这样才能被分辨出来,这也是基于CS的窄带成像分辨率,这一分辨率约束与BP算法相同[4].

下面进一步给出欠采样倍数的下限值.由于本文采用CS理论处理方位欠采样问题,因此欠采样后的脉冲数目应与自旋目标的等效散射点个数K以及信号维度MN有关,三者应满足:

假设方位积累时间为Ta,满采样的重频为PRF,采集脉冲数为Na,欠采样的重频为PRF′,采集脉冲数为,那么PRF′可表示为

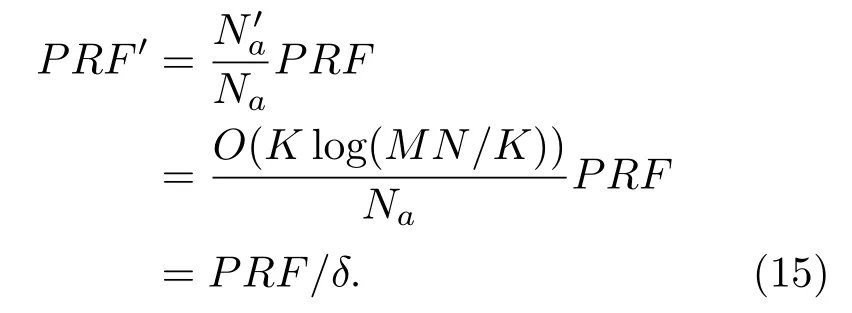
可见系数δ=Na/O(Klog(MN/K))即为理论上的欠采样倍数.现举例说明这一问题.依然假设一大小为1 m的空间碎片,其自旋频率为15 Hz,共包括30个散射点,对一1.5 m×1.5 m的场景进行划分,像素间隔为0.025,那么共划分3600个像素单元,由(14)式计算得至少需要O(144)个脉冲才能保证正确重构.雷达工作于X波段,假设方位积累时间为0.2 s,则保证不产生虚假重构点的PRF至少应为12566 Hz,相应的脉冲数为2513个,代入到(15)式可知欠采样系数δ的下界约为17,可见利用CS理论可保证很高的欠采样条件下对高速自旋目标的精确恢复.

4 仿真与分析

仿真中目标参数设置如下:对28点的螺旋桨形状目标模型进行成像仿真,图3为目标的等效散射点模型,目标的最大散射半径为0.8 m,散射点后向散射强度从中心到边缘依次为0.4,0.6,0.8和1.自旋频率为7.5 Hz.雷达参数设置如下:雷达发射LFM信号,载频为10 GHz,信号带宽为50 MHz,方位积累时间为0.2 s,其PRF以及相应的脉冲数将在不同仿真时分别给出.

图3 自旋目标等效散射点模型Fig.3.Scatterer distribution of spinning target.

仿真中的脉压前噪声统一为高斯白噪声,噪声功率由预设信号回波的平均功率,信噪比为SNR,然后由SNR的计算公式可得到σ2=P×10−SNR/10.

对于成像质量的评价指标.本文以图像熵和目标背景比(target-to-background ratio,TBR)[13]作为量化评价成像质量的指标.

仿真1欠采样率与成像性能关系仿真

基于CS的窄带成像性能与感知矩阵相关性有关,因此这里通过欠采样倍数与感知矩阵相关性的关系来验证欠采样率与成像性能的关系.目标的自旋频率为7.5 Hz,由(5)式计算得此时方位满采样时对应的最小PRF应为5026 Hz,而如此大的PRF常规地基雷达一般是很难满足的.选择目标场景大小为4 m×4 m,相邻散射点间隔为0.1 m,则目标场景共对应于1600个散射点.

CS理论指出,当感知矩阵Θ满足有限等距性质(RIP)时,才能保证稀疏值鲁棒有效的恢复.因此本文首先分析不同欠采样率下感知矩阵的RIP性能.由于RIP验证是一个NP-hard问题,因此本文采取可求解的特征值法[14]来定量衡量感知矩阵性能.仿真时稀疏度从1变化到40,对每一个稀疏度的取值,感知矩阵原子组合方式是随机产生的,本文取1000次蒙特卡罗.降采样倍数分别取4倍和6倍,用相应维度的高斯随机矩阵做对比,图4为仿真结果.

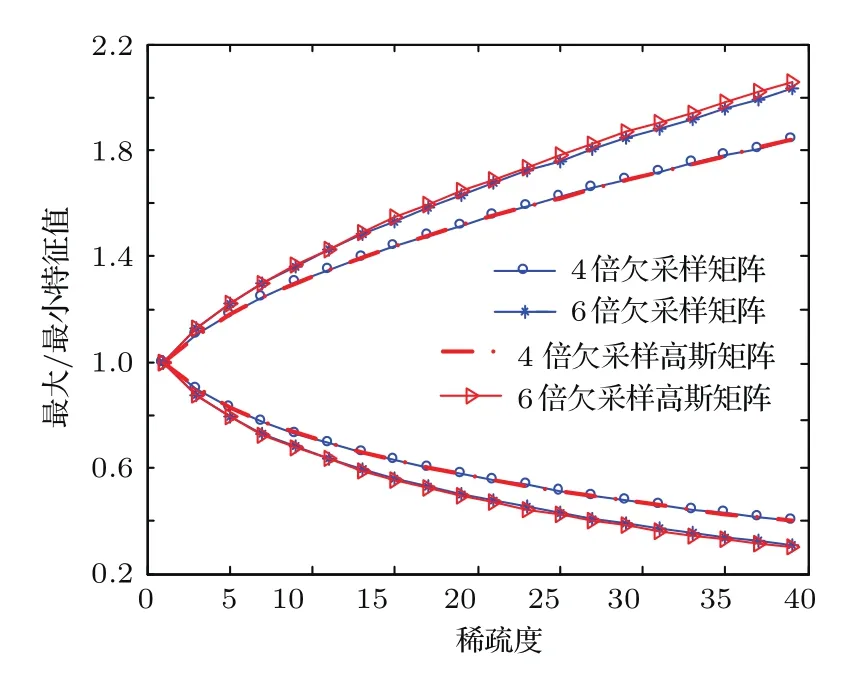
图4 (网刊彩色)不同降采样倍数下感知矩阵特征值对比Fig.4.(color online)Eigenvalues comparision of the sensing matrix in diff erent under sampling rates.

由图4可知:在同一欠采样倍数条件下,欠采样矩阵和相应维度的高斯随机矩阵特征值相差不大,表明本文所使用的欠采样矩阵具有较好的RIP性能;而随着欠采样倍数的增加(从4倍变大到6倍),感知矩阵的最大特征值变大,而最小特征值变小,表明有限等距常数不断增加,意味着感知矩阵RIP性能不断下降.图4的结果表明本文所构建的欠采样感知矩阵Θ具有类似于高斯矩阵的性能,能够满足RIP条件,因此能保证稀疏值鲁棒有效的恢复.此外,如果可以设计RIP性能更好的欠采样方式,那么重构结果质量将提高,这将是下一步工作的研究方向.

仿真2不同欠采样率下的成像效果

本仿真主要验证欠采样率对成像性能的影响.仿真条件与仿真1相同.分别取欠采样倍数为1,5和7,采取BP算法[4]作为对比.图5为均匀欠采样率下不同CS重构算法的成像效果.图6为不同欠采样率条件下的图像熵和TBR.

从不同算法的成像结果对比结果可以看出:随着欠采样倍数的增加,BP算法无法有效地估计所有散射点信息,出现错误估计点较多;而不同的CS重构算法均能在一定的欠采样率条件下获得较好的散射点估计效果.本仿真结果表明,基于CS可实现欠采样下的自旋目标高分辨成像,且可灵活使用各种重构算法,仿真结果验证了基于CS理论的欠采样自旋目标成像的有效性和理论分析.

仿真3分辨率分析

为验证本文关于分辨率分析的有效性,设置仿真条件如下:雷达载频分别设置为1 GHz和10 GHz,对应波长为0.3 m和0.03 m,带宽为50 MHz,假设有两个散射点,其中散射点A的坐标为(0,0),调整散射点B距离A的间隔.为了保证维度较低,选择场景大小为0.7 m×0.7 m,相邻散射点间隔为0.01 m,则目标共对应于4900个散射点.由(14)式计算得到的量测值理论下限值为O(15),本文选取方位样本数为51,满足重构的要求.图7和图8分别为不同的重构算法在不同波长和不同散射点间隔下的成像结果.

由图7以及上文分辨率分析可知,基于CS的欠采样分辨率下限值为0.4λ,当波长为0.3m时,分别率即为0.12 m.从图8的仿真结果可以看出,当散射点间隔小于0.12m时,散射的位置重构误差较大,无法准确地找到散射点的位置;而当散射点的间隔大于0.12m时,则能够准确恢复其位置.仿真验证了上文关于分辨率分析的有效性.从图8可以看出,当波长变小后,间隔为0.1 m的两个散射点能够被准确分辨.仿真验证了基于CS的窄带成像分辨率与波长有关的这一结论.

图5 (网刊彩色)不同欠采样率下的成像效果Fig.5.(color on line)Imaging resu lts of diff erent algorithms in diff erent under sampling rates.

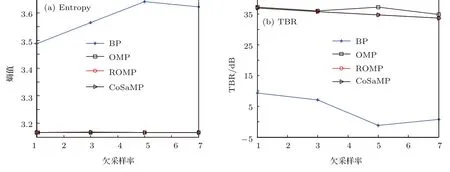
图6 (网刊彩色)不同欠采样率下的成像质量的定量比较Fig.6.(color on line)Quantitative evaluation of the imaging resu lts in diff erent under sampling rates.

仿真4不同带宽条件下的成像效果

本仿真主要验证成像分辨率与带宽的关系.仿真条件和目标场景划分与仿真1相同.发射LFM的带宽分别设置为50,1 MHz,欠采样率为4倍.图9为不同带宽条件下的成像结果.

从图9的结果可以看出,不同带宽条件下的成像结果基本相同.这主要是由于高速自旋目标成像时,主要是利用散射点在方位向上的差异性信息,因此与距离分辨率无关.仿真进一步验证了基于CS进行自旋目标超分辨成像的有效性.

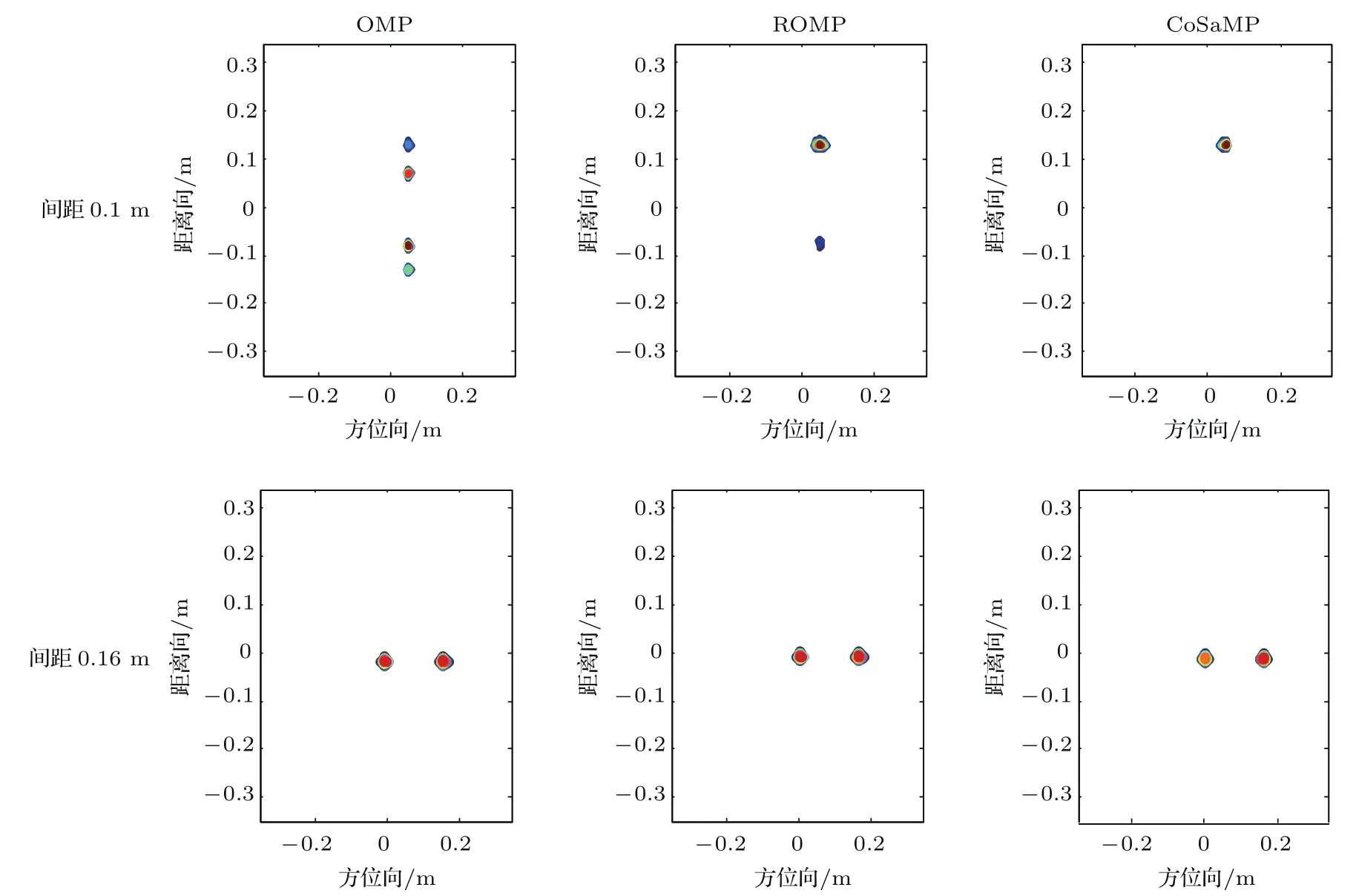
图7 (网刊彩色)波长为0.3 m时不同散射点间隔时的成像结果Fig.7.(color on line)Imaging resu lts of d iff erent algorithms as the wavelength is 0.3 munder d iff erent intervals of the scatterer.

图8 (网刊彩色)波长为0.03 m时不同散射点间隔时的成像结果Fig.8.(color on line)Imaging resu lts of d iff erent algorithms as the wavelength is 0.03 munder d iff erent intervals of the scatterer.

图9 (网刊彩色)不同带宽条件下的成像结果Fig.9.(color on line)Imaging resu lts under d iff erent bandwid th conditions.

5 结 论

常规雷达在观测高速自旋目标时,不可避免地会存在方位欠采样.为实现欠采样且自旋频率未知条件下的高速自旋目标成像,本文对基于CS理论进行欠采样窄带自旋目标的超分辨成像机理进行了物理解释,并给出了一种自旋角速度的估计方法.从本文的分析和仿真结果可以看出,基于CS的自旋目标超分辨成像方法主要有以下两个特征:1)成像机理与常规的成像(如RD算法)方法不同,CS重构在利用不同散射点的多普勒差异性的同时,通过直接寻找散射点“位置”信息的方式避开多普勒频率重构,这种从估计散射点多普勒频率到散射点位置的变化就是基于CS可实现欠采样条件下的超分辨成像的物理机理;2)基于CS理论的成像分辨率和允许的网格失配误差与波长有关,都为0.4λ,且与带宽无关.但是本文在目标模型假设方面只是考虑了简单的散射点模型,且散射点与稀疏基严格匹配.该模型假设较为理想,在后续研究中,将重点分析以下几个方面的问题:

1)当强散射点的位置与稀疏基失配时,如何获得高质量的成像结果,此时可借鉴连续压缩感知的相关理论[15];

2)当目标自旋时散射点由于视角不同以及遮挡效应而发生散射幅度时变时,如何获得高质量图像,此时可借鉴动态压缩感知的相关理论[16];

3)当估计得到的自旋频率存在误差时,如何自适应的进行误差校正与成像.

[1]W ang T,Tong C M,Li X M,Li C Z 2015Acta Phys.Sin.64 210301(in Chinese)[王童,童创明,李西敏,李昌泽2015物理学报64 210301]

[2]Ai X F,Huang Y,ZhaoF,Yang J H,Li Y Z,X iaoS P 2013IEEE Geosci.Remote Sens.Lett.10 362

[3]SatoT1999IEEE Trans.Geosci.Remote Sens.37 1000

[4]Bai X R,Sun G C,W u Q S,X ing MD,BaoZ 2010Sci.China:Inform.Sci.40 1508(in Chinese)[白雪茹,孙光才,武其松,邢孟道,保铮 2010中国科学:信息科学 40 1508]

[5]Bai X R,Zhou F,X ing MD,BaoZ 2011Trans.Aerosp.E lectron.Syst.47 2530

[6]W ang BP,Fang Y,Sun C,Tan X 2015J.Remote Sensing2 254(in Chinese)[王保平,方阳,孙超,谭歆2015遥感学报2 254]

[7]Zhu J,LiaoG S,Zhu S Q 2015J.E lectron.Inform.Technol.37 587(in Chinese)[朱江,廖桂生,朱圣棋2015电子与信息学报37 587]

[8]BaoZ,X ing MD,W ang T2006Radar Imaging Technique(Beijing:Pub lishing House of E lectronics Industry)p24(in Chinese)[保铮,邢孟道,王彤 2006雷达成像技术(北京:电子工业出版社)第24页]

[9]Zhang W P,Li KL,Jiang W D 2015IEEE Sig.Proc.Lett.22 633

[10]Hu J M,Fu Y W,Hu Z G,Li X 2009J.E lectron.Inform.Technol.31 2069(in Chinese)[胡杰民,付耀文,胡志刚,黎湘2009电子与信息学报31 2069]

[11]Bai X R 2011Ph.D.Dissertation(Xi’an:Xidian University)(in Chinese)[白雪茹 2011博士学位论文 (西安:西安电子科技大学)]

[12]Chi Y J,Scharf L L,Pezeshki A,Calderbank R A2011IEEE Trans.Sig.Proc.59 2182

[13]Zhang L 2012Ph.D.Dissertation(X i’an:X idian University)(in Chinese)[张磊 2012博士学位论文 (西安:西安电子科技大学)]

[14]Applebauma L,Howard S D,Searle S,Calderbank R 2009Appl.Comput.Harmon.Ana l.26 283

[15]Yang Z,X ie L H2014 arX iv:14072490v1

[16]Jing N,BiW H,Hu Z P,W ang L 2015Acta Automat.Sin.41 22(in Chinese)[荆楠,毕卫红,胡正平,王林2015自动化学报41 22]

PACS:84.40.Xb,84.40.Ua,07.07.D fDOI:10.7498/aps.66.038401

Analysis on the compressive sensing based narrow-band radar super resolu tion imaging mechan ismof rapid ly spinning targets∗

Li Shao-Dong†Chen Yong-Bin Liu Run-Hua Ma Xiao-Yan

(No.Three Department,Air Force Early W arning Academy,W uhan 430019,China)(Received 13 May 2016;revised manuscript received 25 August 2016)

According tothe characteristics of spinning targets,the narrow-band radar echoes can be directly used for imaging spinning targets.However,spurious peaks appear due toazimuth down sampling with a lowpulse repetition frequency(PRF).By exploiting the sparsity of the targets,the compressed sensing(CS)theory can be adopted toobtain super resolution image under sub-sampling condition.This paper main ly focuses on analyzing the physicalmechanismof the CS-based narrow-band imaging method.Firstly,the narrow-band radar’s under-sampling echoes’model fromrapid ly spinning targets is established.The relationshipbetween CS and the model is analyzed.Then the reasons why the CS-based narrow-band imagingmethod can guarantee the exact recovery of the spinning target are given fromphysical view.The theoretical lower limit of sub-sampling pulse numbers is provided.Finally,the simu lation results verify the eff ectiveness of the theoretical analysis.Themain results obtained in the paper are listed as follows.One is that the mechanismof the CS-based narrow-band imaging method diff ers fromthose of the conventional range Doppler imaging methods.The spurious peaks appear due tocalcu lating the Doppler frequency directly under a lowPRF.Toavoid this phenomenon,the CS-based method searches the positions of the scatterers instead.The variation fromcalcu lating the Doppler frequency directly tosearching the positions of the scatterers is the physicalmechanismof the CS-based super resolution imaging method.The other is that the resolution and the allowab le grid mismatch of the CS-based imaging method are related tothe wavelength,which is 0.4λand unrelated tothe bandwid th.Sothe performance of the CS-based imaging method is related tothe sub-sampling rate,the number of the scatters and the wavelength,and unrelated tothe bandwidth of thewave.However,this paper on ly considers the ideal point scatteringmodeland the grid is perfectly matched with themodel.In the following,three aspects can be further studied.First,due tothe spinning target distribution on a continuous scene,the off-grid problemwould severely aff ect the performance of the CS-based imagingmethod.The continuous compressive sensing theory can be used for solving the off-grid prob lemand explaining the related physical mechanism.Second,the illumination of the radar cannot reach some scatterers on the target in some observation intervals,which results in the occlusion eff ect and the time-varying scattering amplitude.The dynamic CS theory can be used for reference in solving this problem.Finally,if the estimated spinning frequency has error,howtocorrect and compensate for the error adaptively needs tobe further studied.

sub-sampling,compressive sensing,rapid ly spinning targets,super resolution

10.7498/aps.66.038401

∗国家自然科学基金(批准号:61671469)资助的课题.

†通信作者.E-mail:liying198798@126.com

*Project supported by the National Natural Science Foundation of China(G rant No.61671469).

†Corresponding author.E-mail:liying198798@126.com