一种非轴对称磁绝缘电子鞘层边界的计算方法∗

魏浩孙凤举呼义翔梁天学丛培天邱爱慈1)‡

1)(西安交通大学,电力设备电气绝缘国家重点实验室,西安 710049)2)(西北核技术研究所,强脉冲辐射环境模拟与效应国家重点实验室,西安 710024)(2016年6月30日收到;2016年11月20日收到修改稿)

一种非轴对称磁绝缘电子鞘层边界的计算方法∗

魏浩1)2)†孙凤举2)呼义翔2)梁天学2)丛培天2)邱爱慈1)2)‡

1)(西安交通大学,电力设备电气绝缘国家重点实验室,西安 710049)2)(西北核技术研究所,强脉冲辐射环境模拟与效应国家重点实验室,西安 710024)(2016年6月30日收到;2016年11月20日收到修改稿)

长距离磁绝缘传输线内电极偏心、感应腔注入电流非均匀分布引起电子鞘层边界偏心等非对称磁绝缘特性.电子鞘层边界是研究非轴对称磁绝缘特性的重要参数.本文提出一种计算非轴对称磁绝缘电子鞘层边界的方法.通过引入角向非均匀分布的模数,将经典一维轴对称Creedon稳态磁绝缘理论推广应用于圆柱坐标系下二维(r,θ)平面.建立了感应电压叠加器次级非轴对称磁绝缘的二维Creedon物理模型,给出了非轴对称磁绝缘电子鞘层边界的数值计算方法和计算误差.当阴极角向磁场(阴极电流)角向分布满足余弦函数时,电子鞘层边界接近高斯分布.阴极电流角向不均匀程度越大,电子鞘层边界偏心程度越严重,计算误差越大.

磁绝缘感应电压叠加器,注入电流非均匀分布,非轴对称磁绝缘,电子鞘层边界

1 引 言

磁绝缘传输线(magnetically insulated transmission lines,MITL)在超高功率脉冲传输和汇聚中具有重要应用[1−4].大型脉冲功率装置常采用数米至几十米长的MITL,长距离MITL内电极通常仅在首端与装置连接固定,这种悬臂式支撑结构易造成MITL内电极偏心、电极间电/磁场非轴对称分布,从而引起非轴对称磁绝缘[4−7].此外,在磁绝缘感应电压叠加器(magnetically induction voltage adders,MIVA)中,由于感应腔初级注入电流非均匀分布,也会导致MIVA次级磁绝缘呈现非轴对称特性[7−11].

磁绝缘电子鞘层边界是联系MITL微观特性(空间电子电荷密度、电荷质心、漂移速率)和宏观特性(线电压、阴/阳极电流、运行阻抗)的关键参数.电子鞘层边界限定了磁绝缘空间电子的活动区域,可视作MITL的虚阴极,电子鞘层边界和阳极构成的传输线特征阻抗即是MITL的实际运行阻抗[12].沿电子鞘层边界对磁场强度进行环路积分,可获得MITL阳极电流.在非轴对称磁绝缘研究中,电子鞘层边界是评估磁绝缘状态和性能的重要物理量.

在通常的一维、轴对称磁绝缘中,电子鞘层边界是与MITL阴/阳电极共圆心的同心圆 (rs≡常数).对于非轴对称磁绝缘,电子鞘层边界rs(θ)随角向位置呈某种分布,即rs(θ)=f(θ).目前已有的磁绝缘模型(1975年Creedon层流理论[13],1979年Mendel[14]任意动量理论,1990年Lawconnell和Neri[15]通用Laminar理论,2006年Ottinger和Schumer[16]基于粒子模拟修正的Mendel理论,以及2006年Stygar等[17]磁绝缘电子弹性碰撞理论)主要用来描述一维、轴对称磁绝缘问题.由现有模型很难直接获得非轴对称磁绝缘rs(θ)的解析解.

电子鞘层边界rs(θ)也很难直接实验测量,目前主要采用粒子模拟(particle in cell,PIC)方法,通过跟踪大量磁绝缘空间电子的轨迹来确定[16].确定非轴对称磁绝缘的rs(θ)必须采用三维 PIC模型,这对PIC模拟软件及代码提出了较高要求.国外主要采用大型三维粒子模拟软件LSP(large scale procedure),国内电子科技大学研发了三维粒子模拟软件CHIPIC3D,并用于“聚龙一号”装置四层圆盘锥MITL和1 MV LTD装置螺旋支撑杆MITL的三维粒子模拟[18−21].但是,大型脉冲功率装置或器件的三维PIC计算耗时极长,模拟结果因受多种因素和假设条件的影响随机性很大.因此,本文提出了一种确定MIVA次级非对称磁绝缘电子鞘层边界rs(θ)的方法.

2 MIVA次级非轴对称磁绝缘物理模型

图1为MIVA次级MITL横截面(垂直功率传输方向)示意图.rc,ra分别为MITL阴、阳极半径,rs(θ)为待求解的磁绝缘电子鞘层边界.MIVA感应腔初级注入电流非均匀分布导致次级磁绝缘阴/阳极电流、电/磁场角向非轴对称分布[22,23].即使MITL阴/阳电极同轴,仍然会导致rs(θ)偏心[24].

由磁绝缘Creedon层流理论[13],磁绝缘达到稳态时空间电子区域(rc＜r＜rs(θ))和真空区域(rs(θ)＜ r ＜ ra) 的相对论因子γi(r,θ)和γo(r,θ)分别满足数学物理方程[25−28],

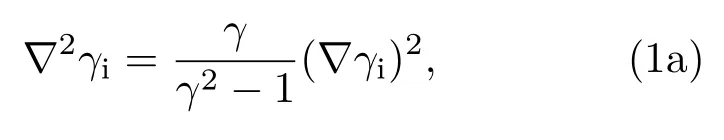
在阴极(r=rc)和阳极 (r=ra)的边界位置,γi(r,θ)和γo(r,θ)分别满足如下边界条件,

其中γ0=1+eV0/(mc2)为阳极的相对论因子,e为电子电荷量,m为电子静止质量,V0为阴-阳电极间线电压.

在电子鞘层边界rs(θ)处,满足分界面衔接条件,

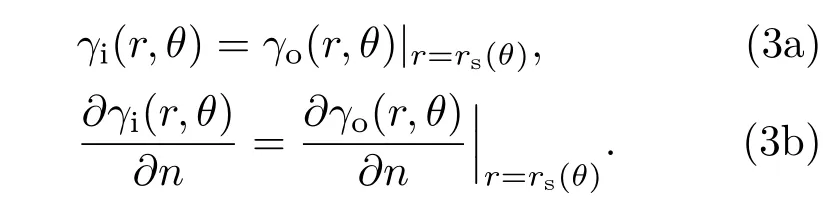
采取分离变量法[29]求解方程(1),考虑到γi(r,θ)和γo(r,θ)在[0,2π]内关于θ= π 对称,并代入边界条件(2),得到相对论因子γi(r,θ)和γo(r,θ)的解析解分别为

其中n为非负整数,表征阴/阳极电流角向非均匀分布的模数,若令n=0,(4)式即为经典的一维、轴对称磁绝缘Creedon层流模型[13,28];系数aj,bj(0≤j≤n,j为整数)为待定常数,其取值与阴/阳极电流角向分布有关.

当给定MITL结构参数(阴/阳极半径ra,rc)、线电压V0和阴极电流角向分布Ic(θ)时,联合方程(3)和(4),可确定电子鞘层边界rs(θ).但因方程(4)为超越方程,难以直接获得rs(θ)的解析解,需要采用数值方法进行求解.

3 计算电子鞘层边界rs(θ)的数值方法

3.1 确定系数aj(0≤j≤n)

由磁绝缘稳态时空间电子径向受力平衡[27],得到

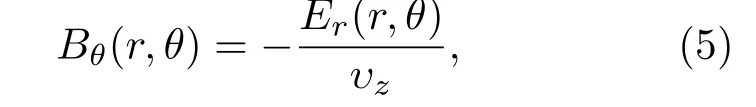
(4)和(5)式联合,得到在rc＜ r＜ rs(θ)区域Bθ(r,θ)满足,

令(6)式中r=rc,得到阴极表面角向磁场Bθ(rc,θ),

采用正交三角函数系cos(jθ)将Bθ(rc,θ)在[0,2π]区间内做Fourier级数展开,得系数aj,其中κ为常数,κ=−erc/mc.

由(8)式可知,系数aj取决于阴极表面角向磁场Bθ(rc,θ)角向分布.实际中,Bθ(rc,θ)角向分布可由感应电压叠加器的电磁模拟或实验测量获得.

3.2 确定系数bj(0≤j≤n)

由方程(3b)可以推导系数bj(0≤j≤n)满足如下矩阵方程,

其中a=(a0,a1,...,an)T和b=(b0,b1,...,bn)T为n+1阶向量.N(rs),M(rs)为(n+1)×(n+1)阶矩阵,其元素分别为

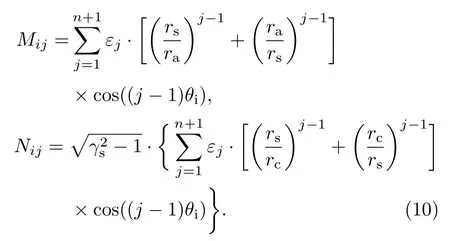
(9)和(10)式的推导过程见附录A.(9)和(10)式表明,当系数aj确定后,系数bj仅与电子鞘层边界rs(θ)有关.因此,可依据MIVA次级磁绝缘电子鞘层边界的物理实际和可能分布,假定rs(θ)满足某种特定的函数分布f0(θ)(如高斯分布、余弦分布、二次抛物线分布等),f0(θ)中含有待定系数.

3.3 确定f0(θ)的待定系数

采用最优化问题的全局搜索解法[30],确定函数f0(θ)中待定系数.最优化问题可表述为

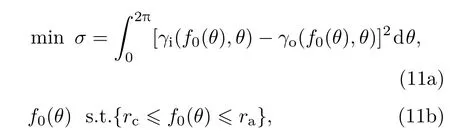
其中(11a)式为最优化问题的目标函数,表征当rs(θ)为假定函数分布f0(θ)时, γi(r, θ)和 γo(r, θ)偏离方程(3a)的程度,定义为计算误差.搜索约束条件(11b)限定了电子鞘层边界的取值范围,即rc＜ f0(θ)＜ra.

3.4 确定电子鞘层边界rs(θ)

重复3.2–3.3节的步骤,比较多种假定函数分布(高斯分布、余弦分布、二次抛物线分布等)的计算误差,计算误差最小的分布视为电子鞘层边界rs(θ).

4 计算方法在MIVA次级非轴对称磁绝缘的应用

给定MIVA次级MITL运行参数:阴极半径rc=0.1 m,阳极半径ra=0.2 m,阴-阳极线电压V0=4 MV,γ0=9,磁绝缘运行在最小电流工作点.

在一维轴对称情况(阴/阳极电流角向均匀分布)下,由磁绝缘经典Creedon层流理论,计算磁绝缘电子鞘层边缘的相对论势γs=2.0,电子鞘层边界rs=0.119 m,阳极电流Ia=132 kA,阴极电流Ic=65.5 kA,阴极表面角向磁场Bco=0.131 T.

二维、非轴对称情况下,由于MIVA感应腔初级注入电流角向的非均匀分布,靠近馈入点的角向位置(θ=0)Bθ(rc,θ)明显偏大,远离馈入点的角向位置(θ= π)Bθ(rc,θ)偏小.假定角向磁场Bθ(rc,θ)满足余弦分布,

其中Bco为一维轴对称(电流角向均匀分布)时阴极角向磁场,不均匀系数δ用于表征二维非轴对称情况下Bθ(rc,θ)角向非均匀分布的程度.

假定MIVA次级MITL电子鞘层边界rs(θ)满足余弦分布、高斯分布和二次抛物线分布,其分布函数分别如(13)–(15)式所示,

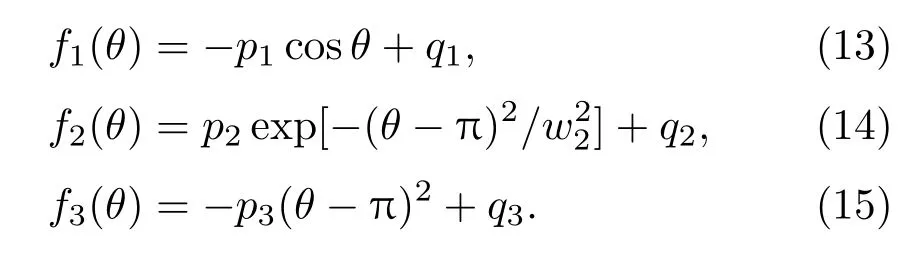
由本文所述的数值计算方法,可以确定f1(θ),f2(θ)和f3(θ)中待定系数.三种假定分布函数下电子鞘层边界rs(θ)如图2所示.余弦、高斯和二次抛物线三种分布函数下的计算误差分别为2.7084,0.0682和9.6110.高斯分布的计算误差最小,因此,当阴极角向磁场Bθ(rc,θ)满足余弦分布时,MITL电子鞘层边界rs(θ)最接近高斯分布.

改变Bθ(rc,θ)角向不均匀系数δ,电子鞘层边界rs(θ)随之变化.表1为几种不均匀系数δ时三种分布函数的计算误差.由表1可知,二次抛物线分布的计算误差最大,高斯分布的计算误差均最小.注入电流分布越均匀(角向磁场Bθ(rc,θ)不均匀系数δ越小),计算误差越小.

当Bθ(rc,θ)不均匀系数δ分别为25%,10% 和2.5%时,采用高斯函数分布求解的电子鞘层边界如图3所示.电子鞘层边界rs(θ)的最大值、最小值和电子鞘层不均匀系数ζ如表2所列,其中电子鞘层角向不均匀系数ζ定义为

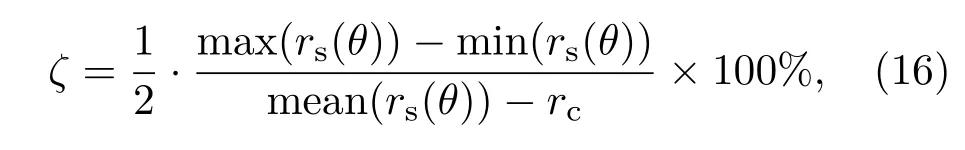
其中max(rs(θ)),min(rs(θ))和mean(rs(θ)) 分别为rs(θ)在θ∈[0,2π]的最大值、最小值和平均值.(16)式定义的ζ物理含义为电子鞘层厚度的极差与平均厚度之比.

图2 (网刊彩色)三种假定分布函数时电子鞘层边界(Bθ(rc,θ)不均匀系数δ=25%)Fig.2.(color online)The electron sheath profi les under the three assumed dstribu tion functions as the asymmetric coffi cient of Bθ(rc,θ),δ,is abou t 25%.

表1 Bθ(rc,θ)不均匀系数δ对计算误差的影响Tab le 1.The in fl uences of the asymmetric coeffi cient of Bθ(rc,θ),δ,on the calcu lation errors.

表2 Bθ(rc,θ)角向不均匀系数δ不同时电子鞘层边界rs(θ)的特性Tab le 2.The parameters of the electron sheath profi les function as the asymmetric coeffi cients of Bθ(rc,θ).

由图3和表2可知,Bθ(rc,θ)不均匀系数δ越大(注入电流角向不均匀程度越大),电子鞘层边界rs(θ)偏心程度越严重.电子鞘层角向不均匀系数ζ与Bθ(rc,θ)角向不均匀系数δ数值相接近.当Bθ(rc,θ)分布较均匀(δ=0.5%)时,电子鞘层边界rs(θ)≈0.119 m,此数值与一维轴对称Creedon理论计算的结果相同.

图3 不同Bθ(rc,θ)角向不均匀系数δ时的磁绝缘电子鞘层边界 (a)δ=25%;(b)δ=10%;(c)δ=2.5%Fig.3.The electron sheath profi les under th ree different asymmetric coeffi cients of Bθ(rc, θ)for(a)δ=25%,(b)δ=10%,and(c)δ=2.5%.

5 结 论

在稳态磁绝缘经典、一维轴对称Creedon理论基础上,引入表征阴/阳极电流角向非均匀分布的参数(角向非均匀分布模数n),建立了圆柱坐标下MIVA次级非轴对称磁绝缘的二维Creedon物理模型,给出了磁绝缘电子鞘层边界rs(θ)的数值计算方法和计算误差.当给定磁绝缘线结构参数(阴/阳极半径)、线电压和阴极电流(阴极角向磁场)角向分布时,可计算磁绝缘电子鞘层边界rs(θ).本文提出的磁绝缘电子鞘层边界确定方法具有计算效率高、耗时短等优点,该方法已用于MIVA次级非轴对称磁绝缘电子鞘层边界的确定.结果表明,当阴极角向磁场Bθ(rc,θ)角向分布满足余弦函数时,电子鞘层边界rs(θ)呈高斯分布.研究了电流均匀性对磁绝缘电子鞘层边界rs(θ)的影响,结果表明,随着电流不均匀程度增加,电子鞘层偏心程度加大;电子鞘层rs(θ)的角向不均匀系数和阴极角向磁场Bθ(rc,θ)的不均匀系数数值相近.

感谢西安交通大学数学学院李东升教授、电气工程学院马西奎教授和葛晓宇博士对数值求解方法给予的良好建议.感谢西北核技术研究所付梅艳、尹佳辉、姜晓峰、曾江涛、张鹏飞、来定国、孙江等的讨论.

附录A 矩阵方程(9)的推导

分界面衔接条件(3)的物理意义是在分界面rs(θ)上,电势和法向电场连续.

当电子鞘层偏心程度较轻(即(rs−rc)/rc≪ 1)时,∂/∂n ∼= ∂/∂r,(3b)式可简化为

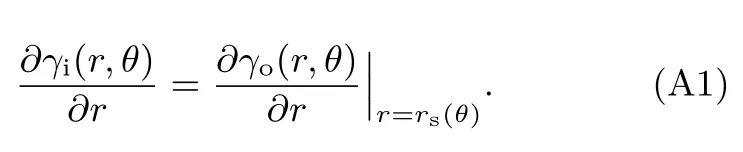
将(4)式中γi(r,θ)和γo(r,θ)表达式代入(A1)式,得到

为了便于分析,将(A2)式等号两边均写成级数求和形成,即

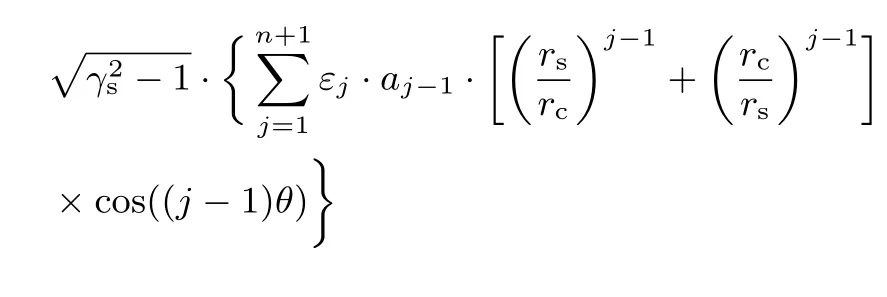
其中

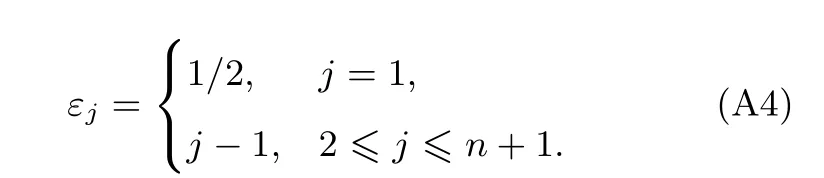
由于方程(A3)对于[0,2π]内任意θ均成立,因此,将θ离散化处理,在[0,2π]取(n+1)个离散点,

对于任意一个θi均满足方程(A3),可以得到,

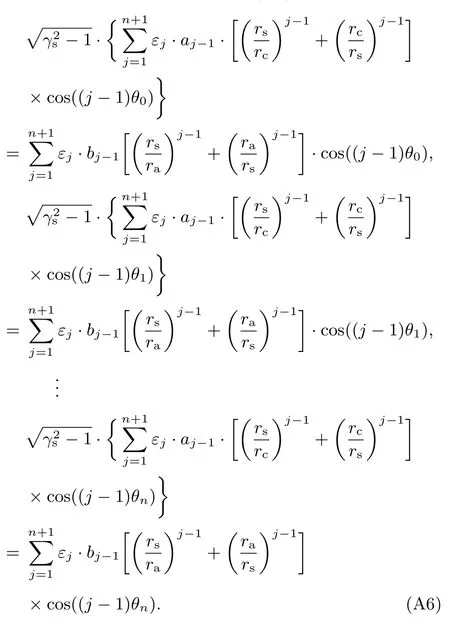
将公式(A6)写成矩阵方程的形式,即

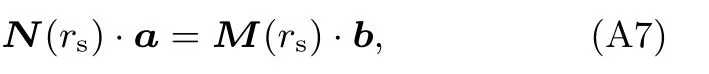
其中,a=(a0,a1,...,an)T和b=(b0,b1,...,bn)T为n+1阶向量;N(rs),M(rs)为(n+1)×(n+1)阶矩阵,其元素分别为

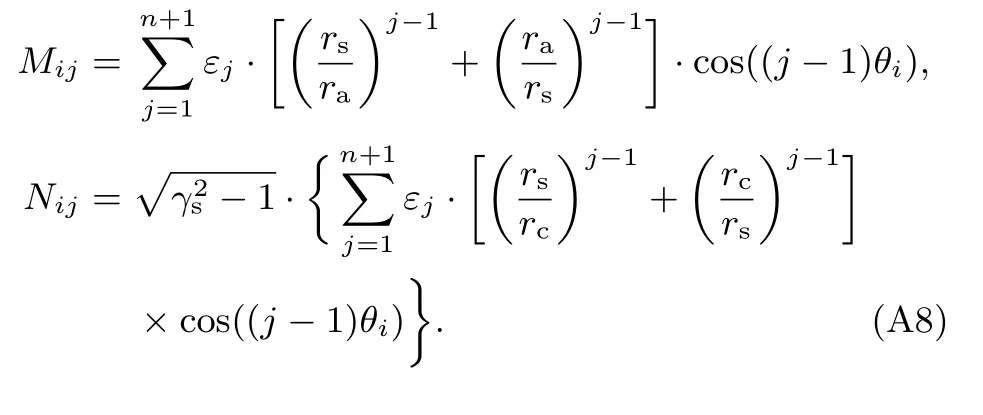
[1]Stygar W A,Corcoran P A,Ives HC,Spielman R B,Douglas JW,W hitney BA,MostromMA,W agoner TC,Speas C S,G illiland TL,Allshouse G A,C lark R E,Donovan G L,Hughes TP,Humph reys D R,JaramilloD M,Johnson MF,Kellogg JW,Leeper R J,Long F W,Martin TH,Mu lville TD,Pelock MD,Pey ton BP,Poukey JW,Ramirez J J,Reynolds P G,Seamen J F,Seidel D B,Seth AP,Sharpe AW,ShoupR W,Smith J W,Vandevalde D M,W av rik R W 2009Phys.Rev.Spec.Top.Accel.Beams.12 120401

[2]Stygar W A,Awe TJ,Bailey J E,Bennett N L,E W Breden,Campbell E M,C lark R E,Cooper R A,CuneoME,Ennis J B,Feh l D L,Genoni TC,Gomez MR,G reiser G W,G runer F R,Herrmann MC,Hutsel BT,Jennings C A,Jobe D O,Jones BM,MC Jones,Jones P A,KnappP F,Lash J S,LeChien KR,Leckbee J J,Leeper R J,Lewis SA,Long FW,LuceroD J,Mad rid E A,Martin MR,Matzen MK,Mazarakis MG,McBride R D,McKee G R,Miller C L,Moore J K,MostromC B,Mu lville TD,Peterson KJ,Porter J L,Reisman D B,Rochau G A,Rochau G E,Rose D V,Rovang D C,Savage ME,Sceiford ME,Schmit P F,Schneider R F,Schwarz J,SefkowAB,Sinars D B,Slutz SA,Spielman R B,Stoltzfus BS,Thoma C,Vesey R A,W akeland P E,W elch D R,W isher ML,W oodworth J R 2015Phys.Rev.Spec.Top.Accel.Beams.18 110401

[3]Zou W K,W ang M,Chen L,Zhou L J,GuoF,X ie W P,Deng J J 2013High Power and Laser and Particle Beams25 2487(in Chinese)[邹文康,王勐,陈林,周良骥,郭帆,谢卫平,邓建军2013强激光与粒子束25 2487]

[4]Pate R C,Patterson J C,Dowd ican MC,Ramirez J J,Hasti D E,Tolk KM,Poukey JW,Schneider L X,Rosenthal SE,San ford TW,Alexander J A,Heath C E 1987Proceeding of 6th IEEE Pu lsed Power ConferenceArlington,USA,22–26 June,1987 p478

[5]Johnson D,Bailey V,Altes R,Corcoran P,Smith I,Cordova S,Hahn K,Maenchen J,Molina I,PortilloS,Puetz E,Sceiford M,Valde D V,Rose D,Oliver B,W elch D,D roemer D 2005Proceeding of 15h IEEE Pu lsed Power ConferenceMonterey,USA,13–17 June,2005 p314

[6]Allen R J,CommissoR J,Cooperstein G,Ottinger P F,Schumer JW 2011Proceeding of 18th IEEE Pu lsed Power ConferenceChicago,USA,19–23 June,2011 p1036

[7]Smith ID 2004Phys.Rev.Spec.Top.Accel.Beams.7 064801

[8]Smith ID,Bailey V L,Fock ler J,Gustwiller JS,Johnson D L,Maenchen J E,D roemer D W 2000IEEE Trans.P lasma Sci.28 1653

[9]Thomas K,Beech P,Brown S,Buck J,Bu rscough J,C lough S,Crotch I,Du ff Y J,Goes C,Huckle I,Jones A,King A,Stringer B,Th readgold J,Trenaman S,W heeldon R,W ood roofe M,Carboni V,DaSilva T,Galver B,G lazebrook W,Hanzel K,Pearce J,PhamJ,Pomeroy S,SaundersW,Speits D,Warren T,W hitney B,W ilson J2011Proceeding of18th IEEE Pu lsed Power ConferenceChicago,USA,19–23 June,2011 p1042

[10]W ei H,Sun F J,Liang TX,Y in J H,Dang TF,Zeng J T,Cong P T,Qiu AC 2014Rev.Sci.Instrum.85 083506

[11]W ei H,Sun F J,Liang TX,GuoJ M,Q iu AC,Cong P T,Y in J H,Hu Y X,Jiang X F,W ang Z G,Dang TF 2015IEEE Trans.P lasma Sci.43 3359

[12]Mendel C W,Rosentha SE 1995Phys.Plasmas2 1332

[13]C reedon J M1975J.Appl.Phys.46 2946

[14]Mendel C W 1979J.Appl.Phys.50 3830

[15]Lawconnell R I,Neri J 1990Phys.F luids B2 629

[16]Ottinger P F,Schumer J W 2006Phys.P lasmas13 063109

[17]Stygar W A,W agoner TC,Ives HC,Corcoran P A,CuneoME,Douglas JW,G illiland TL,Mazarakis MG,Ramirez J J,Seamen J F,Seidel D B,Spielman R B2006Phys.Rev.Spec.Top.Accel.Beams.9 090401

[18]Liu L Q,Liu D G,W ang X Q,Zou W K,Yang C 2012Acta Phys.Sin.61 162901(in Chinese)[刘腊群,刘大刚,王学琼,邹文康,杨超2012物理学报61 162901]

[19]Liu L Q,Liu D G,W ang X Q,Yang C,X ia MZ,Peng K2012Acta Phys.Sin.61 162902(in Chinese)[刘腊群,刘大刚,王学琼,杨超,夏蒙重,彭凯2012物理学报61 162902]

[20]DaiW,Zhu X Z,Liu LQ,Zou W K,GuoF,Liu D G 2015Modern E lectron.Tech.38 144(in Chinese)[戴巍,朱旭智,刘腊群,邹文康,郭帆,刘大刚 2015现代电子技术38 144]

[21]Zou W K,Chen L,Liu D G,Zhang L,Liu L Q,Zhou L J,W ang M,W ei B,GuoF,W ang X Q,Dai Y M,X ie W P,Deng J J 2012Phys.Rev.Spec.Top.Accel.Beams15 110401

[22]Johnson D L,Smith ID,Corcoran P,Bailey V,Maenchen J,Rovang D,Molina I,Hahn K,LuceroR,Kincy M,Kitterman D,Oliver B,W elch D,Rose D,Goldsack TJ,Phillips MA,Sinclair MA,Thomas KJ 2002Proceeding of 14th IEEE High Power Particle Beams ConferenceAlbuquerque,USA,23–28 June,2002 p123

[23]Oliver BV,Genoni TC 2003Proceeding of 14th IEEE Pu lsed Power ConferenceDallas,USA,June 15–18,2003 p395

[24]Bruner N,MostromC,Rose D V,W elch D R,Bailey V,Johnson D L,Oliver BV 2007Proceeding of 16th IEEE Pu lsed Power ConferenceAlbuquerque,USA,June 17–22,2007 p807

[25]Q ian BL,Liu Y G,Li C L,Liu C B2000IEEE Trans.P lasma Sci.28 760

[26]Fuks MI,Schamiloglu E 2014Phys.Plasmas21 053102

[27]BluhmH(translated by Jiang W H,Zhang C)2008Pu lsed Power Systems:Principles and Application(Beijing:Tsinghua University Press)pp128–135(in Chinese)[布鲁姆H著(江伟华,张弛译)2008脉冲功率系统的原理与应用 (北京:清华大学出版社)第128–135页]

[28]W ang MY 1978Appl.Phys.Lett.33 284

[29]Ma X K2000Theory and Application of Electromagnetic Field(X i’an:X ian Jiaotong University Press)pp206–216(in Chinese)[马西奎 2000电磁场理论及应用(西安:西安交通大学出版社)第206–216页]

[30]Xue D Y Chen Y Q 2011Technology and Application of SystemSimu lation Based on MATLABand Simu link(Beijing:Tsinghua University P ress)pp108–110(in Chinese)[薛定宇,陈阳泉 2011基于MATLAB/Simu link的系统仿真技术与应用(北京:清华大学出版社)第108–110页]

PACS:84.70.+p,07.85.Fv,41.20.–q,52.35.–gDOI:10.7498/aps.66.038402

Amethod tocalcu late the electron sheath profi le of the nonaxisymmetricalmagnetic insu lation∗

Wei Hao1)2)†Sun Feng-Ju2)Hu Yi-Xiang2)Liang Tian-Xue2)Cong Pei-Tian2)Qiu Ai-Ci1)2)‡

1)(State Key Laboratory of E lectrical Insu lation and Power Equipment,X i’an Jiaotong University,X i’an 710049,China)2)(State Key Laboratory of Intense Pu lsed Rad iation Simu lation and Effect,Northwest Institute of Nuclear Technology,Xi’an 710024,China)(Received 30 June 2016;revised manuscript received 20 November 2016)

The nonaxisymmetricalmagnetic insulation would occur due tothe disalignment of inner electrodes in longmagnetically insulated transmission lines,or the nonuniformdistributionsof injected currents in induction cavities ofmagnetically insulated induction voltage adders(MIVA).The electron sheath profi le is a very important parameter tocharacterize the nonaxisymmetricalmagnetic insulation.In the past,the three-dimensional particle in cell simu lation was usually used todetermine the electron sheath profi le,which is extremely time-consuming and ineffi cient.In this paper,a fast and effi cient calcu lation method is proposed.The classical one-dimensional Creedon theory of the magnetic insu lation equilibriumis generalized toa two-dimensional plane of(r,θ)via introducing a parameter defined as the azimuthalmode number.Two-dimensional Creedon is developed tomodel the asymmetric magnetic insulation of the MIVA.Provided the azimuthal distributions ofmagnetic fl ux density on the cathode,which is in proportion tothe cathode current,the two-dimensional Creedon model is numerically solved.Anumerical solution method tocalculate the electron sheath profi le is proposed,and then the calculation error is alsogiven.As the azimuthal distribution ofmagnetic flux density on the cathodemeets a cosine function,the profi le of the electron sheath is approximate tothe Gauss function.As the nonuniformportion of cathode current increases,the electron sheath becomesmore eccentric,and the calculation error is alsomuch larger.

magnetically insulated induction voltage adders,asymmetrical distribution of injected currents,nonaxisymmetricalmagnetic insulation,electron sheath profi le

10.7498/aps.66.038402

∗国家自然科学基金(批准号:11505138,51577156)资助的课题.

†通信作者.E-mail:weihaoyy@nint.ac.cn

‡通信作者.E-mail:qiuac@cae.cn

*Project supported by the National Natural Science Foundation of China(G rant Nos.11505138,51577156).

†Corresponding author.E-mail:weihaoyy@nint.ac.cn

‡Corresponding au thor.E-mail:qiuac@cae.cn