基于多目标模糊规划的灌区多水源优化配置

付 强 肖圆圆 崔 嵩 刘 东 李天霄

(东北农业大学水利与土木工程学院，哈尔滨150030)

基于多目标模糊规划的灌区多水源优化配置

付 强 肖圆圆 崔 嵩 刘 东 李天霄

(东北农业大学水利与土木工程学院，哈尔滨150030)

以黑龙江省和平灌区为例，构建基于多目标模糊规划的灌区多水源优化配置模型，该模型能够在提高农业灌溉用水净效益的同时有效减少农业灌溉水量，促进和平灌区多水源高效配置。采用具有非线性隶属度函数的模糊多目标规划求解模型，得到不同流量不同水源下的最优配水方案。结果表明:不同流量水平下水稻不同生育阶段均存在缺水现象，低流量下需从柳河水库引入外调水才能保证水稻的最小需水量。为保证灌区整体效益，按照引水工程、提水工程、井灌工程的先后顺序进行配水，并得到多目标配水模型在不同情景下的运行稳定情况。该模型可以高效地进行灌区多水源在作物各生育阶段的优化配置。

多目标模糊规划;多水源;优化配置;灌区

引言

如何协调好灌区水资源的供需关系，确保水资源合理高效利用，是水资源领域研究的热点问题［1］。灌区多水源优化配置可以理解为基于作物需水量和不同水源的可供水量，通过调整不同水源的配水量，以实现农业灌溉用水与农业收益统筹提高的目的［2］。黑龙江省是我国重要的商品粮基地，粮食作物的播种面积逐年增长，粮食生产消耗的灌溉水量也逐年增加［3－4］，如何科学地优化且合理地配置有限的灌溉水资源对提高黑龙江省灌区水资源利用效率和保障粮食安全具有十分重要的意义［5］。

近年来，国内外关于灌区水资源优化配置的研究不断涌现，其中灌区水资源多目标配置由于能够对多个相互矛盾的目标进行科学、合理的优选而备受关注［6－9］。常见的多目标优化方法有目标法［10］、加权和法［11］、理想点法［12］、模糊优选理论［13］、模糊多目标规划法［14］、遗传算法［15－18］、人工鱼群算法［19］、粒子群算法［20－21］等。模糊多目标规划法由于较强的操作性和灵活性至今仍被广泛应用于各领域［22－23］，但多数研究只探讨线性模糊隶属度函数的解法，忽略了隶属度函数的非线性特点对优化结果的影响。本文在前人研究的基础上，构建同时考虑灌溉效益和水资源利用率的灌区多水源优化配置模型，并采用基于非线性隶属度函数的模糊多目标规划方法求解模型，以期实现灌区多流量多水源在作物不同生育阶段内的高效配水。

1 原理介绍

1.1 模型建立

灌区水资源优化配置中，管理者需要将灌区不同水源有限的水资源量在作物各个生育阶段内进行优化配置，从而达到用尽可能少的水量获得较高的产量或收益的目的。在优化配置中，需考虑不同水源的可供给量、水量平衡、供水目标、作物需水量等约束，为此，需构建基于多目标模糊规划的灌区多水源优化配置模型。所构建模型包括2个目标函数，目标函数1为灌区作物净效益最大，目标函数2为灌溉用水量最小，目标函数1和目标函数2的结合可促进灌区用水效率的提升。模型表达式为:

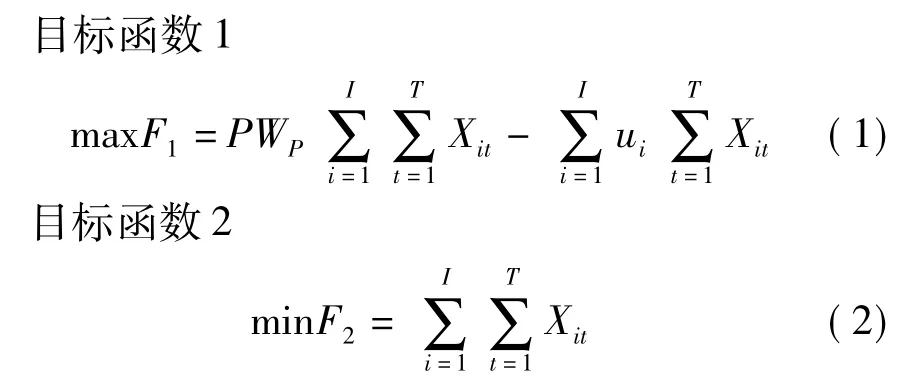
约束条件:

式中 P——作物市场单价，元/kg

WP——灌溉水分生产率，kg/m3

I——供水工程类别总数，分别代表引水工程、提水工程、井灌工程，取3

T——配水周期(即作物生育期)类别总数，分别代表分蘖期、拔节期、抽穗期、乳熟期，取4

Xit——i供水工程在t生育期的配水量(决策变量)，m3

ui——i供水工程的供水成本，元/m3

Qit——i供水工程在t生育期的可用水量，m3

Rt－1、Rt－2——t－1、t－2生育期的余水量，m3

Wit——i供水工程在t生育期的供水目标，m3

WL——灌溉需水量下限值，m3

WU——灌溉需水量上限值，m3

1.2 模型求解

采用模糊多目标规划对上述多目标模型进行求解。然而，在实际情况中，很难确定模糊多目标规划中隶属度函数的性质。不失一般性，采用非线性隶属度函数对所构建模型的2个目标函数进行表示(图1)。

令f表示任意的目标函数，则相应的非线性隶属度函数可表示为:

越大越优型

越小越优型

图1 非线性隶属度函数Fig．1 Nonlinearmembership functions

式中 μf(x)——f的隶属度函数

fU、fL——目标函数的最大、最小值

β1、β2——非线性隶属度函数的形状系数

β1、β2=1表示线性，β1、β2＞1和 0＜β1、β2＜1表示非线性［24］。引入变量λ，则原模型的目标函数可通过隶属度函数的形式，即(μfn(X))βn≥λ(0≤λ≤1)转换成约束条件，与原有约束条件一起构成一个目标函数为maxλ的单目标模型。对于本文所构建模型，目标函数1为经济效益最大，属于越大越优型，其隶属度函数采用式(8)计算，目标函数2为灌溉用水量最小，属于越小越优型，其隶属度函数采用式(9)计算。根据上述原理，所构建多目标模型可转换成如下单目标模型形式:

目标函数

约束条件

式中 F1max、F1min——目标函数1的单目标模型目标函数的最大值和最小值

F2max、F2min——目标函数2的单目标模型目标函数的最大值和最小值

2 实例研究

2.1 研究区概况

和平灌区位于黑龙江省绥化市庆安县中部，呼兰河左岸的干支流河漫滩及一级阶地上，灌区范围由东向西呈带状分布。该灌区主要水源有地表水与地下水，取水方式又可分为3种供水工程，即引水工程、提水工程和井灌工程，井灌工程由地下水提供，其他2个供水工程由地表水提供，柳河水库为外调水源。水稻是和平灌区的主要作物［25］，其生育期主要包括返青期、分蘖期、拔节期、抽穗期、乳熟期、黄熟期，其中返青期和黄熟期的腾发量都较小，因此，本文根据水稻生育期需水量需求，将3种供水工程的水量优化分配到水稻的分蘖期、拔节期、抽穗期、乳熟期4个生育期。

2.2 基础数据确定

根据《呼兰河灌区工程初期设计报告》以及当地水务局提供的调研数据，对水稻不同生育阶段需水量以及各供水工程灌溉控制面积进行分析，得到各供水工程的供水目标以及水稻充分灌溉条件下的需水量上、下限值;综合分析灌区内多年降水量和径流统计资料，获得不同流量水平下水稻各生育期各供水工程的可用水量，基础数据见表1和表2［26］。

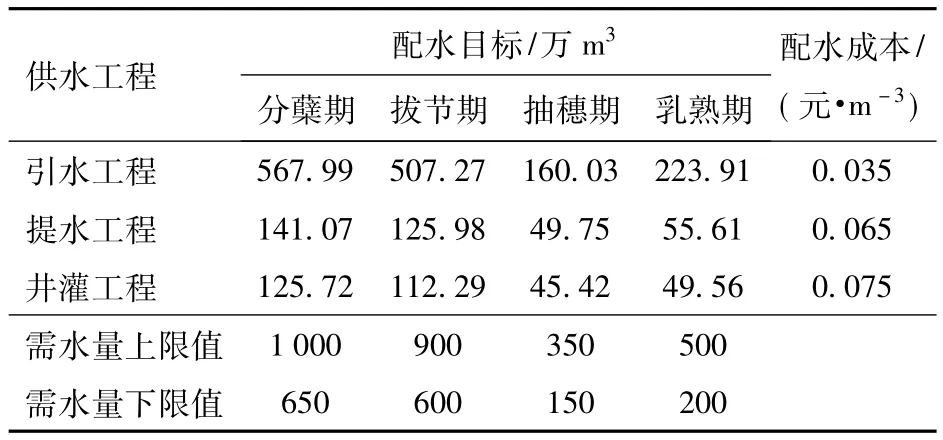
表1 不同生育阶段各供水工程的配水目标与需水量临界值Tab．1 Water supply targets and water demand thresholds for water supply projects at different grow th stages

表2 不同生育阶段各供水工程的可用水量Tab．2 Available water of water supp ly projects at different grow th stages

3 模型结果与分析

3.1 隶属度为线性情况

根据上述原理，运用LINGO11对模型进行求解。得到不同β1和β2组合下不同流量3种供水工程在不同生育期的最优配水量，以β1=1、β2=1，即隶属度函数为线性情况为例，模型运行结果见表3。从表中可以看出，3个水源中，引水工程和提水工程在4个生育期内都有配水，而井灌工程则为部分生育期不予配水，高流量水平下，只有在拔节期井灌工程才有配水。这是由于井灌工程的供水费用在3个供水工程中是最高的，在能够保证作物各生育期最低需水量的前提下，水量分配顺序为优先采用引水工程，其次采用提水工程，最后采用井灌工程。另外，模型运行结果是作物净效益最大和灌溉用水量最小2个目标综合作用的结果，以寻求用水效益和用水量之间的平衡，达到综合效益最优。以中流量为例，若单纯追求作物净效益最大，则3个供水工程在4个生育期均有分配，若只考虑灌溉用水量最小，则提水工程和井灌工程在抽穗期和乳熟期均未配水，这2个生育期的最小需水量仅由引水工程来满足，综合考虑2个目标函数，提水工程在穗期和乳熟期有配水，但配水量较单纯考虑经济效益最大目标下有所调整，井灌工程在这2个生育期则不配水。高流量、中流量的总配水量分别为 1 860万 m3、1 730万m3，低流量下由于3个水源的总可供水量满足不了水稻的最小需水量要求，需要从柳河水库调水190万m3，调水后，低流量的最优总配水量为1 643万m3。图2(图中S1、S2、S3、S4分别代表分蘖期、拔节期、抽穗期、乳熟期)为各流量水平下作物各生育期的缺水量，即平均需水量与最优配水量之间的差值。3个流量水平下均存在缺水现象，高流量、中流量和低流量下总缺水量分别为315万m3、445万m3和532万m3。

表3 β1=1和β2=1组合情况下模型最优配水结果Tab．3 Results of optimalwater distribution under β1=1 andβ2=1

图2 不同流量水平下不同生育阶段的配水量与平均需水量Fig．2 Water allocation and average water demand under different flow levels and growth stages

3.2 隶属度为非线性情况

上述分析了β1=1和β2=1，即模糊多目标规划中隶属度函数为线性的配水结果，实际上，目标函数非线性隶属度函数也是常见的，如图1所示。本文将β1和β2进行如下组合来分析不同情景下配水方案的变化。情景1:令β1=1，β2=0.3，0.5，0.7，1，3，7，10依次变化;情景2:令β2=1，β1=0.3，0.5，0.7，1，3，7，10依次变化。图3(图中P1、P2、P3分别代表引水工程、提水工程和井灌工程)为2种情景下3种水源在不同流量下的最优配水量，图3a为情景1的结果，图3b为情景2的结果。对于情景1，高流量水平下的引水工程配水量保持不变，提水工程配水量在β1为0.3～7之间有略微下降趋势，井灌工程在这期间配水量均为零。但在β2=10时发生显著变化，提水工程和井灌工程配水量均有大幅度提升，表明对于高流量水平，当β1=1、β2=10情景下模型稳定性较差，决策者在进行决策时，应避免这种情景。中流量和低流量下的引水工程和提水工程配水量均维持稳定状态，井灌工程配水量有略微调整，但变化不显著。对于情景2，在β2=1下，从β1=7开始3个流量水平下的3个供水工程的配水量均发生显著变化，表明在这种情景下，β1＞7时模型稳定性发生变化。在β1＜7的各组合情景中，高流量的引水工程和井灌工程的配水量保持不变，提水工程配水量随β1的增大有增大趋势;中流量下引水工程配水量保持不变，提水工程和井灌工程配水量随β1的增大有增大趋势;低流量下引水工程和提水工程配水量保持不变，井灌工程的配水量随β1的增大有增大趋势，上述结果表明，引水工程的配水量是最稳定的，井灌工程的配水量最不稳定，尤其是在低流量水平下具有较大的敏感性。以中流量为例，图4为不同情景组合不同流量水平下不同生育期的配水量变化情况，β1=1时，拔节期在任意β2情况下的配水量均保持不变，分蘖期、抽穗期和乳熟期在β2≤1的情况下略微变化，在β2＞1的情况下趋于稳定。β2=1时，分蘖期和拔节期的配水量均保持稳定，抽穗期和乳熟期在β1＜7时略微变化，β1＞7时趋于稳定。不同的情景组合会导致不同的配水量结果，决策者可根据实际情况结合个人偏好做出最终决策。

图3 不同情景组合下3种供水水源在不同流量水平下的配水量变化情况Fig．3 Water allocation changes under differentwater sources，flow levels and scenarios

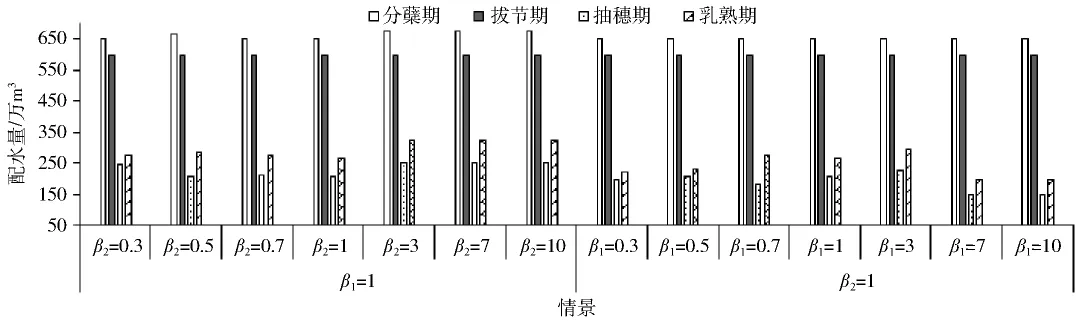
图4 不同情景组合不同流量水平下不同生育期的配水量变化情况Fig．4 Water allocation changes under different growth stages and scenarios

4 结论

(1)根据和平灌区水源特点，构建多水源多目标配水模型，将不同水源(包括引水工程、提水工程和井灌工程)的可供水量在水稻各生育期内进行高效配置，以达到用尽可能少的灌溉水资源量获得尽可能大的经济效益的目的。

(2)采用模糊多目标规划方法对模型进行求解，结果显示灌区按照引水工程、提水工程、井灌工程的先后顺序进行配水。模型得到了灌区用水效益和用水量之间的平衡，在综合效益最优情况下，3个流量水平下均存在缺水现象，低流量情况下需从柳河水库调入190万m3水才能保证水稻的最小需水量。

(3)重点探讨了多目标模型目标函数的模糊不确定性，用非线性隶属度函数进行量化，通过模型目标函数不同非线性隶属度函数的情景组合，讨论了模型在不同情景下的运行稳定情况。引水工程的配水量相对稳定，而井灌工程在低流量水平下对目标函数隶属度函数的非线性程度具有较大的敏感性。

参 考 文 献

1 姜秋香，付强，朱长虹，等．基于多维临界调控理论的水资源优化配置研究进展［J］．东北农业大学学报，2015，46(7):103－108．JIANG Qiuxiang，FU Qiang，ZHU Changhong，et al．Research progress of water resources optimal allocation based on theory of multidimensional critical regulation and control［J］．Journal of Northeast Agricultural University，2015，46(7):103－108．(in Chinese)

2 李晨洋，张志鑫．基于区间两阶段模糊随机模型的灌区多水源优化配置［J］．农业工程学报，2016，32(12):107－114．LIChenyang，ZHANG Zhixin．Multi-water conjunctive optimal allocation based on interval-parameter two-stage fuzzy-stochastic programming［J］．Transactions of the CSAE，2016，32(12):107－114．(in Chinese)

3 付强，刘巍，刘东，等．黑龙江省灌溉用水效率指标体系空间格局研究［J/OL］．农业机械学报，2015，46(12):127－132．http:∥www．j-csam．org/jcsam/ch/reader/view_abstract．aspx?flag=1＆file_no=20151218＆journal_id=jcsam．DOI:10．6041/ j．issn．1000-1298．2015．12．018．FU Qiang，LIUWei，LIU Dong，etal．Spatial distribution of irrigation water use efficiency index system in Heilongjiang Province［J/ OL］．Transactions of the Chinese Society for Agricultural Machinery，2015，46(12):127－132．(in Chinese)

4 付强，刘烨，李天霄，等．水足迹视角下的黑龙江省粮食生产用水分析［J/OL］．农业机械学报，2017，48(6):184－192．http:∥www．j-csam．org/jcsam/ch/reader/view_abstract．aspx?flag=1＆file_no=20170624＆journal_id=jcsam．DOI:10．6041/j．issn．1000-1298．2017．06．024．FU Qiang，LIU Ye，LI Tianxiao，et al．Analysis of water utilization in grain production from water footprint perspective in Heilongjiang Province［J/OL］．Transactions of the Chinese Society for Agricultural Machinery，2017，48(6):184－192．(in Chinese)

5 李茉，姜瑶，郭萍，等．考虑不同层次利益主体的灌溉水资源优化配置［J/OL］．农业机械学报，2017，48(5):199－207．http:∥www．j-csam．org/jcsam/ch/reader/view_abstract．aspx?flag=1＆file_no=20170225＆journal_id=jcsam．DOI:10．6041/j．issn．1000-1298．2017．05．025．LIMo，JIANG Yao，GUO Ping，et al．Irrigation water optimal allocation considering stakeholders of different levels［J/OL］．Transactions of the Chinese Society for Agricultural Machinery，2017，48(5):199－207．(in Chinese)

6 张智韬，刘俊民，陈俊英，等．基于RS、GIS和蚁群算法的多目标渠系配水优化［J］．农业机械学报，2010，41(11):72－78．ZHANG Zhitao，LIU Junmin，CHEN Junying，et al．Water resources allocation of canal system based on multi-objective about RS，GISand ant colony algorithm［J］．Transactions of the Chinese Society for Agricultural Machinery，2010，41(11):72－78．(in Chinese)

7 聂相田，邱林，周波，等．井渠结合灌区水资源多目标优化配置模型与应用［J］．节水灌溉，2006(4):26－31．NIE Xiangtian，QIU Lin，ZHOU Bo，et al．A multi-objective optimal allocation model for water resources in well-canal combined irrigated area and its application［J］．Water Saving Irrigation，2006(4):26－31．(in Chinese)

8 赵恩龙．基于多目标遗传算法的灌区水资源优化调度研究［D］．武汉:长江科学院，2013．ZHAO Enlong．Study of optimalwater resources allocation of irrigation district based on multi-objective genetic algorithm evolution［D］．Wuhan:Changjiang River Scientific Research Institute，2013．(in Chinese)

9 LIM，GUO P，SING V P．Biobjective optimization for efficient irrigation under fuzzy uncertainty［J］．Journal of Irrigation and Drainage Engineering，2016，142(8):05016003．

10 吴慧，吕一兵．一类非线性二层多目标规划问题的主要目标法［J］．西南大学学报:自然科学版，2016，38(1):109－115．WU Hui，LYibing．Themain targetmethod for solving a class of nonlinear bilevelmulti-objective programming problems［J］．Journal of Southwest University:Natural Science Edition，2016，38(1):109－115．(in Chinese)

11 乔辰，张国立．几何加权法求解多目标规划问题［J］．华北电力大学学报:自然科学版，2011，38(6):107－110．QIAO Chen，ZHANG Guoli．Geometric weighting method for solving multi-objective programming problems［J］．Journal of North China Electric Power University:Natural Science Edition，2011，38(6):107－110．(in Chinese)

12 龚懿，张礼华．基于理想点法的灌区多目标种植结构优化模式研究［J］．现代农业科技，2014(13):211－218．GONG Yi，ZHANG Lihua．Research on multi-objective mode optimization of planting structure in irrigation area based on ideal pointmethod［J］．Modern Agricultural Science and Technology，2014(13):211－218．(in Chinese)

13 黎坤，陈晓宏，江涛，等．多目标系统模糊优选理论在城市饮用水源地选址中的应用［J］．中山大学学报:自然科学版，2005，44(4):120－123．LIKun，CHEN Xiaohong，JIANG Tao，etal．Application ofmulti-objective system fuzzy optimization theory to selecting table-water resources in city［J］．Acta Scientlarum Naturalium Universitatis Sunyatseni，2005，44(4):120－123．(in Chinese)

14 邹进，张勇传．三峡梯级电站短期优化调度的模糊多目标动态规划［J］．水利学报，2005，36(8):925－931．ZOU Jin，ZHANG Yongchuan．Short-term optimal scheduling of cascade hydropower stations using fuzzy multi-objective dynamic programming［J］．Journal of Hydraulic Engineering，2005，36(8):925－931．(in Chinese)

15 孙月峰，张胜红，王晓玲，等．基于混合遗传算法的区域大系统多目标水资源优化配置模型［J］．系统工程理论与践，2009，29(1):139－144．SUN Yuefeng，ZHANG Shenghong，WANG Xiaoling，et al．Multi-objective optimization of regionalwater resources based on mixed genetic algorithm［J］．Systems Engineering—Theory＆Practice，2009，29(1):139－144．(in Chinese)

16 游进军，纪昌明，付湘．基于遗传算法的多目标问题求解方法［J］．水利学报，2003，34(7):64－69．YOU Jinjun，JIChangming，FU Xiang．New method for solvingmulti-objective problem based on genetic algorithm［J］．Journal of Hydraulic Engineering，2003，34(7):64－69．(in Chinese)17 陈南祥，李跃鹏，徐晨光．基于多目标遗传算法的水资源优化配置［J］．水利学报，2006，37(3):308－313．CHEN Nanxiang，LIYuepeng，XU Chenguang．Optimal deployment of water resources based on multi-objective genetic algorithm［J］．Journal of Hydraulic Engineering，2006，37(3):308－313．(in Chinese)

18 王鹏．基于Pareto Front的多目标遗传算法在灌区水资源配置中的应用［J］．节水灌溉，2005(6):29－32．

19 高玉芳，张展羽．混沌人工鱼群算法及其在灌区优化配水中的应用［J］．农业工程学报，2007，23(6):7－11．GAO Yufang，ZHANG Zhanyu．Chaotic artificial fish-swarm algorithm and its application in water use optimization irrigated areas［J］．Transactions of the CSAE，2007，23(6):7－11．(in Chinese)

20 张文明，董增川，朱成涛，等．基于粒子群算法的水文模型参数多目标优化研究［J］．水利学报，2008，39(5):528－534．ZHANGWenming，DONG Zengchuan，ZHU Chengtao，et al．Automatic calibration of hydrologic model based on multi-objective particle swarm optimization method［J］．Journal of Hydraulic Engineering，2008，39(5):528－534．(in Chinese)

21 周建中，李英海，肖舸，等．基于混合粒子群算法的梯级水电站多目标优化调度［J］．水利学报，2010，41(10):1212－1219．ZHOU Jianzhong，LIYinghai，XIAO Ge，et al．Multi-objective optimal dispatch of cascade hydropower stations based on shuffled particle swarm operation algorithm［J］．Journal of Hydraulic Engineering，2010，41(10):1212－1219．(in Chinese)

22 MORANKAR D V，RAJU K S，KUMAR D N．Integrated sustainable irrigation planning with multiobjective fuzzy optimization approach［J］．Water Resource Management，2013，27(11):3981－4004．

23 TEEGAVARAPU R SV，FERREIRA A R，SIMONOVIC SP．Fuzzymultiobjectivemodels for optimal operation of a hydropower system［J］．Water Resource Research，2013，49(6):3180－3193．

24 SASIKUMAR K，MUJUMDAR PP．Fuzzy optimization model forwater qualitymanagement of a river system［J］．Journal ofWater Resources Planning and Management，1998，124(2):79－88．

25 李丹，李德丽，颜华．用水农户参与水利灌溉管理的冲量过程分析［J］．东北农业大学学报，2013，44(8):116－121．LIDan，LIDeli，YAN Hua．Impulse process analysis ofwater users participate in irrigationmanagement［J］．Journal of Northeast Agricultural University，2013，44(8):116－121．(in Chinese)

26 付强，刘银凤，刘东，等．基于区间多阶段随机规划模型的灌区多水源优化配置［J］．农业工程学报，2016，32(1):132－139．FU Qiang，LIU Yinfeng，LIU Dong，et al．Optimal allocation ofmulti-water resources in irrigation area based on interval-parameter multi-stage stochastic programmingmodel［J］．Transactions of the CSAE，2016，32(1):132－139．(in Chinese)

Multi-water Resources Optimal Allocation of Irrigation District Based on Fuzzy Multi-objective Programm ing

FU Qiang XIAO Yuanyuan CUISong LIU Dong LITianxiao
(School ofWater Conservancy and Civil Engineering，Northeast Agricultural University，Harbin 150030，China)

Many problems，such as the shortage of water resources and the low operating efficiency of water project，are ubiquitous in an irrigation district with multi-water resources．Therefore，it is significant and necessary to implement joint dispatching of multi-water resources to alleviate water shortage and promote the synergy ascension of water resources productivity．Taking Heping irrigation district in Heilongjiang Province as an example，a fuzzy multi-objective programming for multi-water resources optimal allocation model was constructed．The proposed model was capable of increasing water net benefit and decreasingwater-use amount simultaneously，which would improve the effective allocation ofmulti-water resources of Heping irrigation district．Fuzzy multi-objective programming with nonlinear membership functions was adopted to solve the model，and the optimal water allocation schemes under different flow levels and water sourceswere obtained．Results showed thatwater shortage existed in each growth period of rice under each flow level，and more water should be transferred from Liuhe reservoir under low flow level to guarantee the minimum water requirement．Water were allocated to rice in the order ofwater diversion project，water lifting project and well irrigation project to ensure the total benefit of Heping irrigation district．The stability of themulti-objectivemodel operation under different scenarios was obtained and analyzed in detail．Water allocation of water diversion project was relatively stable，while water allocation of well irrigation project had higher sensitivity for nonlinearity of membership function of the objective function under low flow level．The developed model can effectively allocate multi-water resources to the different growth stages of rice，which would provide reasonable decision schemes for the corresponding administrative departments．

fuzzy multi-objective programming;multi-water resources;optimal allocation;irrigation district

TV213.4;O221.6

A

1000-1298(2017)07-0222-06

2016-12-14

2017-01-17

国家自然科学基金项目(51479032、51279031、51609039)、黑龙江省高校长江学者后备支持计划项目、黑龙江省水利科技项目(201318、201503)和国家重点研发计划项目(2017YFC0406002)

付强(1973—)，男，教授，博士生导师，主要从事农业水土资源优化利用与管理研究，E-mail:fuqiang0629@126．com

10．6041/j．issn．1000-1298．2017．07．028