基于梯度矢量流的柔顺机构拓扑图轮廓提取方法*

付永清，张宪民

(华南理工大学 a.设计学院；b.机械与汽车工程学院，广州 510640)



基于梯度矢量流的柔顺机构拓扑图轮廓提取方法*

付永清a，张宪民b

(华南理工大学 a.设计学院；b.机械与汽车工程学院，广州 510640)

提出一种基于梯度矢量流模型的柔顺机构拓扑图的轮廓提取方法。该方法首先通过密度再分配求出单元节点密度，然后，利用差分方法计算出单元节点密度的梯度，之后，相继求出节点的外能、传统外力和梯度矢量流。在模型演化过程中，利用双线性插值算法求出任意点的GVF，同时，针对拓扑图的孔所处的不同位置，给出了不同的初始模型及相应的模型演化方法，实现了柔顺机构拓扑图轮廓的自动提取。最后，数值算例表明了文中算法的可行性。

梯度矢量流；柔顺机构；拓扑图轮廓提取

0 引言

拓扑图的轮廓提取是柔顺机构拓扑图提取过程中的主要问题之一。现有的拓扑图轮廓提取的方法，图像解释方法[1-6]、密度轮廓方法[7-11]和几何重构方法[12]，在这三类方法中，大多数都需要手工取点，降低了整个设计过程的速度，因此需要发展一种自动化程度较高的拓扑图轮廓提取方法。又由于拓扑结构形状复杂，其中的孔可能存在于设计域的内部或周边，并且拓扑结构常存在曲率较高的角点，这些都是拓扑图轮廓提取中的难点。此外，基于水平集的拓扑优化方法[13-14]无须显式地提取拓扑图轮廓，但是由于这一方法具有初始敏感性、不能生成新孔、计算效率低和难以收敛到不光滑的角点等缺陷，导致不能得到满意的轮廓提取结果。因此，对柔顺机构来说，在拓扑优化到形状优化的综合设计过程中，尽可能地减少人工干预，快速、自动提取出有较高精度边界的拓扑图已变得越来越重要和具有挑战性。

在图像处理和计算机视觉等领域，由Kass等人[15]提出的参数活动轮廓模型已经成为图像分割、轮廓提取和边缘检测等的重要方法。但是，参数活动轮廓模型的局限性在于外力捕捉范围小，因此它对轮廓的初始位置很敏感，不同的初始位置可能导致不同的收敛结果，所以，为了得到正确的提取结果，初始模型应放置在所期望的边界附近；该模型的第二个局限性是模型能量函数的表达形式使其难以较好地收敛到图形的凹陷区域；此外，模型的参数较多，各参数的选择需要根据实际问题确定。为了克服这些问题，研究人员对活动轮廓模型及其求解算法进行了改进，使这种方法的应用范围得到很大扩展[16-19]。

因此，本文研究了基于梯度矢量流模型的柔顺机构拓扑图轮廓提取方法。该方法首先通过密度再分配求出单元节点密度，然后，利用差分方法计算出单元节点密度的梯度，之后，相继求出节点的外能、传统外力和梯度矢量流。在模型演化过程中，利用双线性插值算法求出任意点的GVF，同时，针对拓扑图的孔所处的不同位置，给出了不同的初始蛇模型及相应的模型演化方法，实现了柔顺机构拓扑图轮廓的自动提取。

1 GVF活动轮廓模型

GVF(Gradient Vector Flow)是一种同时从两个方向捕获图像边缘的外部力场，图像外力定义为Fext=V(x,y)，其中V(x,y)=(u(x,y),w(x,y))为梯度矢量流场，GVF活动轮廓模型的能量函数表示为[20-21]：

(1)

式中，权值μ为归一化的参数，f(x,y)是由灰度图或二值图定义的边缘图，通常可取为：

f(x,y)=-Eext(x,y)

(2)

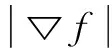
由变分法，梯度矢量流V可通过如下的欧拉方程求解[20，21]：

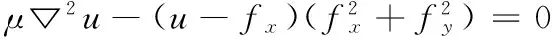
(3)

ut(x,y,t)=μ▽2u(x,y,t)-(u(x,y,t)-

fx(x,y))(fx(x,y)2+fy(x,y)2)

wt(x,y,t)=μ▽2w(x,y,t)-(w(x,y,t)-

fy(x,y))(fx(x,y)2+fy(x,y)2)

(4)

将式(4)重写为：

ut(x,y,t)=μ▽2u(x,y,t)-b(x,y)u(x,y,t)+c1(x,y)

wt(x,y,t)=μ▽2w(x,y,t)-b(x,y)w(x,y,t)+c2(x,y)

b(x,y)=fx(x,y)2+fy(x,y)2

c1(x,y)=b(x,y)fx(x,y)

c2(x,y)=b(x,y)fy(x,y)

(5)

式中fx(x,y)和fy(x,y)可利用图像的梯度算子或差分方法求解，设i,j,n分别对应于x,y,t，并设x,y方向的空间采样步长分别为Δx,Δy，时间采样步长为Δt，则式(5)中的偏导数可近似为：

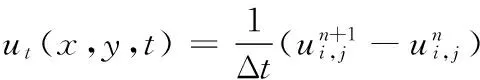
(6)

其迭代求解方程为：

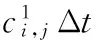
(7)

式中，

(8)

为了使式(7)获得稳定解，参数r通常应满足r≤1/4，并且时间步长Δt应满足：

(9)

由于梯度矢量流场不仅扩展了传统活动轮廓模型的外力作用范围，增加了轮廓初始化的灵活性，而且，在一定程度上改善了其在图像凹陷处的收敛效果，因此，本研究采用基于梯度矢量流的活动轮廓模型进行拓扑图轮廓的提取。

2 节点密度的计算

由于机构截面尺寸较小，所以轮廓曲线应为没有厚度的曲线，因此活动轮廓的各点不能取为整个密度单元，而应该取节点或单元内的某一数据点(x,y)。因而，必须首先根据单元密度计算设计域内各节点的密度。本文采用文献[22]和[23]的方法，将节点密度表示为邻域单元归一化密度的平均值，即：

(10)

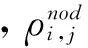
(11)

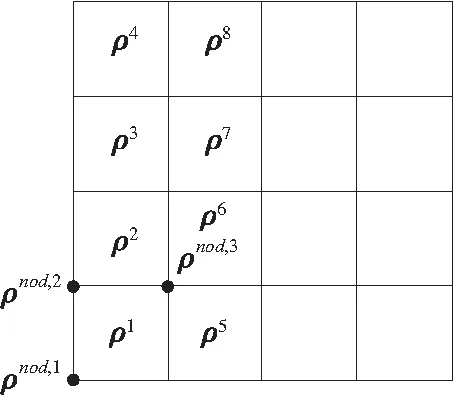
图1 节点密度图解

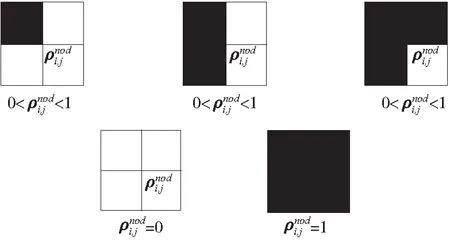
图2 节点密度的三种类型

3 设计域内任意点的梯度矢量流计算

3.1 单元节点的梯度矢量流计算

为了计算设计域内任一点的外力，必须首先求出各单元节点密度的梯度。考虑到节点密度为离散数据，因此，用节点密度的差分代替微分。假设设计域节点阵列大小为m×n，对于设计域内部节点，用中心差分近似其梯度，可得:

(12)

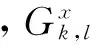
(13)

(14)

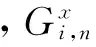
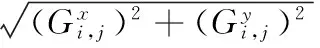
(15)

又由于节点外能为离散值，因此，仍用差分近似其梯度，从而，可得设计域内各节点的外力，再进一步迭代计算出设计域内各节点的GVF。

3.2 基于双线性插值的任意点的GVF计算

由于活动轮廓的各点是在梯度矢量流的作用下向目标边界演化，而这些点可能位于设计域内的单元节点或其它任意位置，因此，本文根据单元节点的GVF，利用双线性插值求模型演化过程中任意点的GVF。

设任意待求点的坐标为(x,y)，首先对该点坐标进行取整操作，以获得其所在单元左上角节点的坐标(i,j)，设dx=x-i，dy=y-j，因此，点(x,y)的GVF可由设计域中坐标为(i,j)、(i+1,j)、(i,j+1)及(i+1,j+1)的四个节点的规一化GVF确定，即:

(16)

式中，(ue(x,y),we(x,y))、(ue(i,j),we(i,j))、(ue(i+1,j),we(i+1,j))、(ue(i,j+1),we(i,j+1))和(ue(i+1,j+1),we(i+1,j+1))分别为点(x,y)及节点(i,j)、(i+1,j)、(i,j+1)、(i+1,j+1)的规一化GVF。

4 拓扑图轮廓的提取

4.1 拓扑图内部封闭轮廓的提取

一般地，拓扑结构形状复杂，其中的孔可能位于设计域的内部或周边。对于设计域内部的孔，其轮廓是封闭的，GVF场的节点落在封闭轮廓的内部，如图3[24]所示，该节点可看成是轮廓曲线的膨胀中心，为了使模型收敛到正确的边界，初始轮廓曲线应包围GVF场的节点，并且，可以是任意形状的封闭曲线。在能量最小化过程中，梯度矢量流在以节点为中心的360°范围内推动曲线上各点向外移动，使活动轮廓模型最终收敛到拓扑图的边界。

图3 包含内节点的轮廓的变形

4.2 拓扑图外部开环轮廓的提取

4.2.1 活动轮廓初始化

对于拓扑图周边孔区域，由于仅其中一部分曲线是待提取的拓扑图轮廓，因此属于开环轮廓，并且，这时GVF场的节点位置在孔的外部，梯度矢量流对轮廓曲线的作用范围小于180°，如图4所示[24],所以，无论采用开环或封闭模型提取轮廓，都不能使模型在期望的范围内膨胀，以至于不能提取出拓扑图的全部边界。因此，这些区域的模型初始化及曲线演化都比设计域内部孔区域的情形复杂得多。为此，本文对这类拓扑图轮廓的提取按以下过程进行，首先，采用封闭的GVF活动轮廓模型提取位于设计域周边孔区域的完整轮廓，然后再去除多余边界，仅保留所需的拓扑图轮廓。在活动轮廓初始化阶段，考虑到GVF场的节点位置在孔的外部，以及梯度矢量流的作用范围较小，导致整个轮廓曲线在收敛过程中都往一个方向偏移，使轮廓提取的结果不能遍及孔的全部边界的问题，将初始GVF活动轮廓模型设置为多边形，并使多边形的相应边与设计域边界重合[21]。

图4 不包含内节点的轮廓的变形

4.2.2 活动轮廓演化算法的改进

为了使GVF活动轮廓的收敛结果能遍及所期望的拓扑图边界，对于设计域周边孔的模型演化采用了两个策略，一是在曲线演化过程中，活动轮廓位于边界上的点均保持固定不动；二是采用固定点偏移算法，该算法的作用是扩大GVF模型的膨胀区域。以待提取的孔的轮廓与设计域有一条边重合的情形为例，并设重合边与x轴平行，如图5所示，其中图5a为第i次迭代过程中，模型仅在GVF作用下的膨胀结果，图5b为对图5a中的活动轮廓施加固定点偏移算法之后的结果。对比图5a与图5b，可见固定点偏移算法能有效改进活动轮廓膨胀效果。该算法的实施过程可表示如下[25]：

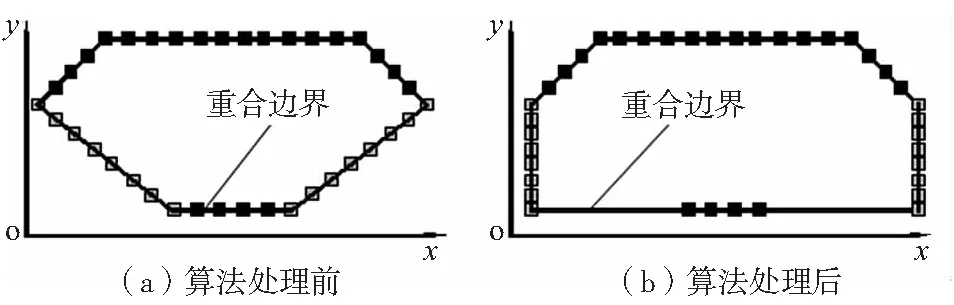
图5 固定点偏移算法

(1)对于i=1,…,N

如果 点(x,y)不是边界点，存储该点在N个蛇点中的序号，生成矩阵N1；

将矩阵N1中各点的x坐标生成新的矩阵X1；

寻找矩阵X1中最小的x值；

确定minx1在X1中所对应的序号m1；

(2)对于i=1,…,N如果 点(x,y)是边界点,存储该点在N个蛇点中的序号,生成矩阵N2；

将矩阵N2中各点的x坐标生成新的矩阵X2；

寻找矩阵X2中最小的x值minx2；

确定minx2在X2中所对应的序号m2；

(3)根据矩阵N1、N2以及序号m1、m2求出与minx1、minx2对应的y1、y2。对于i=1,…,N,将落在(minx1,y1)与(minx2,y2)之间的点均移动到点(minx1,y1)的正下方。

4.2.3 多余边界的去除

提取设计域周边孔区域的完整轮廓之后，需要去除多余边界，保留所需的拓扑图轮廓。仍以待提取的孔的轮廓与设计域有一条边重合的情形为例，并设重合边与x轴平行，则去除多余边界的算法步骤如下[25]：

(1)对于i=1,…,N,如果点(x,y)是边界点，存储该点,在N个蛇点中的序号，生成矩阵N1；

(2)将矩阵N1中各点的x坐标生成新的矩阵X1；

(3)寻找矩阵X1中最小的x值minx1和最大的x值maxx1；

(4)对于i=1,…,N,如果点(x,y)不是边界点，存储该点,在N个蛇点中的序号，生成矩阵N2；

(5)在矩阵N2中添加x值分别为minx1和maxx1的点。

(6)调整矩阵N2的元素顺序，使x值分别为minx1和maxx1的点成为开曲线的首末点。

5 算例

如图6所示为柔顺夹持器机构设计域，大小为400μm×400μm，材料的杨氏模量为200E/GPa，泊松比为0.3，输入载荷Fin为200mN，目标体积约束比θ为0.3，过滤半径为2.5，单元边长5μm，输入输出弹簧刚度分别为5N/mm。由于设计域具有对称性，因此取一半进行研究，并将其离散为80×40的有限元网格。柔顺夹持器机构的对称一半拓扑图如图7所示。从该图可知，拓扑优化结果中共有7个孔区域，其中4个位于设计域内部，具有封闭轮廓，另外3个孔在设计域的周边，具有开环轮廓。因此，首先采用GVF活动轮廓模型提取设计域内部4个孔的封闭轮廓，轮廓初始化及提取过程如图8a～图8h所示，然后，结合本文的多边形初始化和固定点偏移算法提取设计域周边3个孔的封闭轮廓，图9a～图9f所示为轮廓初始化及提取过程，最后，从提取结果中去除多余轮廓，并补充拓扑结构的直线边界，因此，拓扑图轮廓提取结果如图9g所示，进一步可得图10所示的柔顺夹持器的完整轮廓，从图中可以看出，本文算法得到了较光滑的拓扑图轮廓提取结果，说明本文算法是可行的。

图6 柔顺夹持器机构设计域

图7 柔顺夹持器机构拓扑图

图8 柔顺夹持机构拓扑图闭环轮廓提取

图9 柔顺夹持机构拓扑图开环轮廓提取

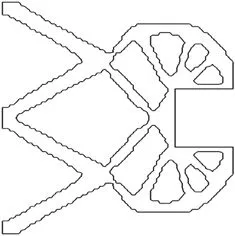
图10 柔顺夹持机构的完整轮廓

6 结论

提出一种基于梯度矢量流模型的柔顺机构拓扑图的轮廓提取方法。该方法首先通过密度再分配求出单元节点密度，然后，利用差分方法计算出单元节点密度的梯度，之后，相继求出节点的外能、传统外力和梯度矢量流。在模型演化过程中，利用双线性插值算法求出任意点的GVF，同时，针对拓扑图的孔所处的不同位置，给出了不同的初始蛇模型及相应的模型演化方法，实现了柔顺机构拓扑图轮廓的自动提取。最后，数值算例表明了本文算法得到了较光滑的拓扑图轮廓提取结果，说明本文算法是可行的。

[1] Papalambros P, Chirehdast M. An integrated environment for structural configuration design [J].J Eng Des 1990,1:73-96.

[2] Bendsøe MP, Rodrigues HC. Integrated topology and boundary shape optimization of 2-D solid [J]. Comput Methods Appl Mech Eng 1991,87:15-34.

[3] Olhoff N, Bendsøe MP, Rasmussen J. On CAD-integrated structural topology and design optimization [J]. Comput Methods Appl Mech Eng 1991,89:259-279.

[4] Bremicker M, Chirehdast M, Kikuchi N, et al. Integrated topology and shape optimization in structural design [J]. Mech Struct Mach 1991,19:551-587.

[5] Chirehdast M,Gea H C,Kikuchi N,et al. 1994: Structural configuration examples of an integrated optimal design process. J. Mech. Design 116, 997-1004.

[6] Lin C-Y, Chao L-S. Automated image interpretation for integrated topology and shape optimization [J]. Struct Multidiscip Optim 2000,20:125-137.

[7] Jang GW, Kim KJ, Kim YY. Integrated topology and shape optimization software for compliant MEMS mechanism design [J]. Advances in Engineering Software 2008,39:1-14.

[8] Kumar AV, Gossard DC. Synthesis of optimal shape and topology of structures [J]. J Mech Des 1996,118:68-74.

[9] Youn SK, Park S-H. A study on the shape extraction process in the structural topology optimization using homogenized material [J]. Comput Struct 1997,62(3): 527-38.

[10] Hsu YL, Hsu MS, Chen CT. Interpreting results from topology optimization using density contours[J]. Comput Struct 2001,79:1049-58.

[11] Hsu MH, Hsu YL. Interpreting three-dimensional structural topology optimization results[J]. Computers and Structures 2005; 83:327-337.

[12] Tang P-S, Chang K-H. Integration of topology and shape optimization for design of structural components[J]. Struct Multidisc Optim 2001,22:65-82.

[13] Zhu B, Zhang X and Fatikow S. Structural topology and shape optimization using a level set method with distance-suppression scheme[J]. Computer Methods in Applied Mechanics and Engineering, 2015, 283: 1214-1239.

[14] Zhu B, Zhang X, Wang N, et al. Optimize heat conduction problem using level set method with a weighting based velocity constructing scheme[J]. International Journal of Heat and Mass Transfer, 2016, 99: 441-451.

[15] Kass M, Witkin A, Terzopoulos D. Snakes: active contour models [J]. Internat. J Comput. Vision, 1988,1(4):321-331.

[16] Scott GL. The alternative snake—and other animals [R]. The 1987 Stockholm Workshop on Computational Vision, Stockholm (J-O Eklundh, Ed.), Dept. of Numerical Analysis and Computing Science, Royal Institute of Technology, TRITA-NA-P8714 CVAP 47.

[17] Leitner F, Marque I, Lavall′ee S, et al. Dynamic segmentation: Finding the edge with differential equations and “spline snakes” [R]. Technique Report TIMBTIM 3-IMAG, Faculte De Medecine, La Tronche, France, 1990.

[18] Cohen LD, Cohen I. Finite element methods for active contour models and balloons for 2-D and 3-D images [J]. IEEE Transaction on Pattern Analysis and Machine Intelligence, 1993, 15(11): 1131-1147.

[19] Lilian Ji, Hong Yan. Robust topology-adaptive snakes for image segmentation [J]. Image and Computing, 2002, 20:147-164.

[20] Xu C, Prince JL. Gradient vector flow:a new external force model for snakes [J]. IEEE Proceedings of Conference on Computer Vision and Pattern Recognition, 1997:66-71.

[21] Xu C, Prince JL. Snakes, shapes, and gradient vector flow [J]. IEEE trans image process, 1998, 7:359-369.

[22] Youn SK, Park SH. A study on the shape extraction process in the structural topology optimization using homogenized material [J]. Computers and Structures, 1997, 62(3): 527-538.

[23] Hsu MH, Hsu YL. Interpreting three-dimensional structural topology optimization results [J]. Computers and Structures, 2005, 83:327-337

[24] He Y, Luo YP, Hu DC. Semi-automatic initialization of gradient vector flow snakes [J]. Journal of Electronic Imaging, 2006,15(4), 043006.

[25] 付永清. 柔顺机构拓扑与形状优化设计中的拓扑图提取理论和方法研究[D]. 广州：华南理工大学，2009.

(编辑 李秀敏)

A Topological Contour Extraction Approach for Compliant Mechanisms Based on the Griadient Vector Flow

FU Yong-qinga,ZHANG Xian-minb

(a.School of Design;b. School of Mechanical and Automotive Engineering, South China University of Technology, Guangzhou 510640,China)

Based on the griadient vector flow, a topological contour extraction approach for compliant mechansimsis proposed. Firstly, element node densities are computed by a density redistribution. Then, the grads of node densities are obtained by the difference method. Subsequently, the external energy and triditional enternal force and griadient vector flow. During the evolving process of the model, bilinear interpolation is used to calculate the griadient vector flow of a random point, Aiming to different position of holes in the topology, different initialization and evolving methods for the model are developed, So automation contour extraction for the topologies of compliant mechanisms is realized. At last, numerical examples are used to confirm the feasibiligy of the proposed approach.

griadient vector flow；compliant mechansimsis; topological contour extraction

1001-2265(2017)07-0055-05

10.13462/j.cnki.mmtamt.2017.07.013

2016-09-18；

2016-10-29

国家自然科学基金 (51275174)

付永清(1968—)，女，江西高安人，华南理工大学副教授，博士，研究方向为机构优化设计和拓扑图提取，(E-mail)yqfu@scut.edu.cn。

TH112;TG506

A