基于后验风险的多源先验信息融合方法

陈洪科

（厦门大学嘉庚学院，福建漳州363105）

基于后验风险的多源先验信息融合方法

陈洪科

（厦门大学嘉庚学院，福建漳州363105）

针对多源先验信息Bayes融合中先验分布权重分配问题，提出了一种基于后验风险的权重确定方法——构造后验风险矩阵，并基于后验风险与先验分布权重成反比的原则建立权重求解方程进而求得各先验分布的权重系数。通过算例证明了该方法的有效性。

多源信息融合；后验风险；Bayes；可靠性

Bayes方法在产品的小子样可靠性评定中得到了非常广泛的应用。该方法的显著特色与优点在于能够利用产品先验信息，例如工程实践中长期积累的经验、专家意见以及历史可靠性信息等。然而，其优点也是实际应用的难点所在，如何有效地融合多种验前信息，从而得到合理的综合先验分布进行统计推断，是一个受到普遍重视问题。

多源先验信息融合的关键在于确定不同先验分布在综合先验分布中的合理权重。典型方法包括由专家确定各先验分布在融合中的权重、由各先验信息可信度确定权重[1-2]、自助融合估计法（Bootstrap方法或随机加权方法）[3]。这些方法具有良好的工程应用价值，但也存在不足之处：专家确定权重难以保证精度，主观性较大[4]；先验信息可信度的确定在某些情况下比较困难，适用范围有限；自助融合估计方法以先验信息的可信度为基础，不仅存在可信度难以确定的问题，而且通过直方图确定先验分布的做法受主观因素干扰。近年来，针对这些方法的应用改进持续进行，同时也出现了基于D-S证据理论、第2类极大似然估计原理（ML-II）、分布图、概率模型等的新方法[5-8]。本文基于Bayes统计理论中“后验风险”概念提出了一种多源先验信息融合方法，下面给出具体论述。

1 多源先验信息的Bayes融合

假设某产品寿命服从参数为θ的分布，其密度函数记为f（t｜θ）。为了评估该产品的可靠性水平，现抽取n个样本进行现场试验。一般得到的试验数据为截尾数据，不妨记为X，其中r个样本失效，失效时间序列为t1≤t2≤…≤tr，其余的n-r个在时间ts截尾（定数截尾时，ts=tr；定时截尾时，ts即定时时间）。

如果现场试验之前已获取了m源先验信息，经转化得到m个先验分布πi（θ）（i=1，2，…，m）。假设已知每个先验分布的权重，记作w=（wi）1×m，其中wi即是分布πi（θ）的权值且所有权值之和为1。那么融合各先验分布得到的综合先验

由上述数据模型可得似然函数

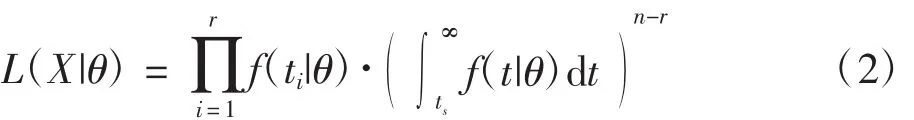
而先验分布πi（θ）下的后验分布则是根据Bayes定理，融合后验分布

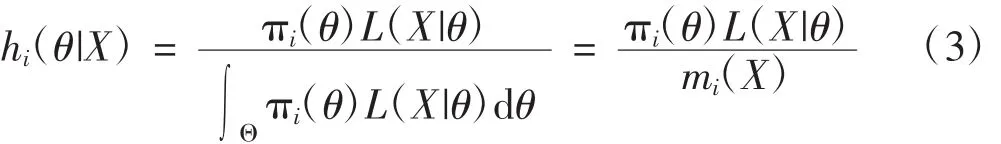
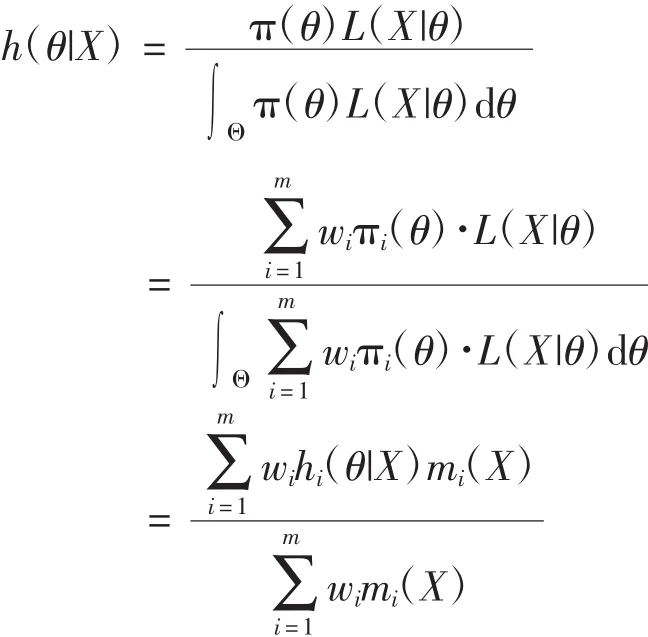
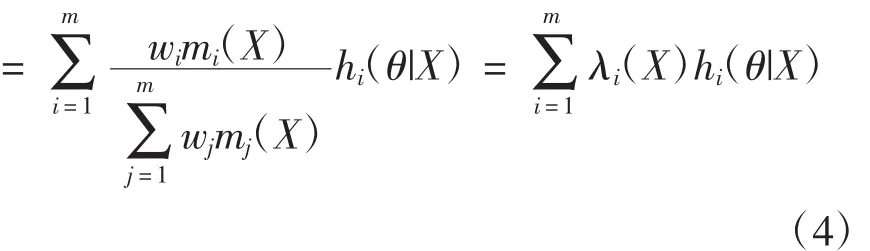
（4）式的计算结果表明，融合后验分布是不同先验信息源下后验分布的加权和。在平方差损失函数下，参数θ的融合后验估计

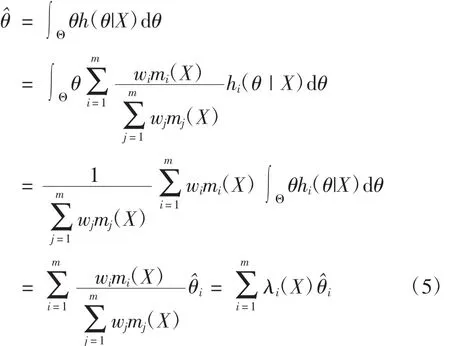
（5）式的计算结果表明，融合后验估计也是不同先验信息源下后验估计的加权和。显然，利用这种融合后验分布进行Bayes统计决策分析是比较便利的。

2 权值计算

Bayes决策分析中常用“后验风险”作为评定估计量的好坏的标准[9]。一般地，如果参数先验分布越接近真实分布，那么由Bayes定理计算得到的参数估计便越接近真实值。直观地想，不同先验分布的精确度不同，利用它所得的参数估计的精度也不同。在相同的损失函数下，参数估计越精确，采纳该估计所承担的风险也就越小，该先验分布的权重也就越高。因此，可以用后验风险来衡量权值的大小。当然，为了能够比较，还需对其作一些扩展。

假设计算中采用平方差损失函数

对于任一先验分布πi（θ），由它算得的参数估计值

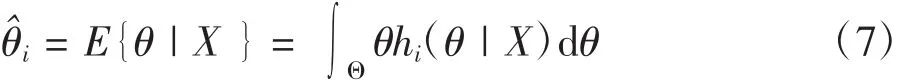
根据文献[9]，此估计量对现场数据X的后验风险

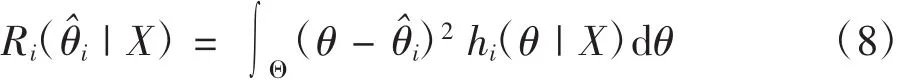
为了能纵向地比较不同先验分布下所得参数估计的后验风险，将（8）式修改为

当i=j时，Rij就是一般意义上的后验风险。不妨记

称之为后验风险矩阵。（9）式与（8）式的主要不同在于利用融合后验分布h（θ｜X）而非hj（θ｜X）来计算后验风险。这样做既能提高后验风险的计算精确度，又为不同先验分下布后验风险的比较提供了一个基准。

依前所述，先验分布后验风险越小，其权值越大；反之，其权值越小，因此后验风险的比值与权值的比值成反比，即有

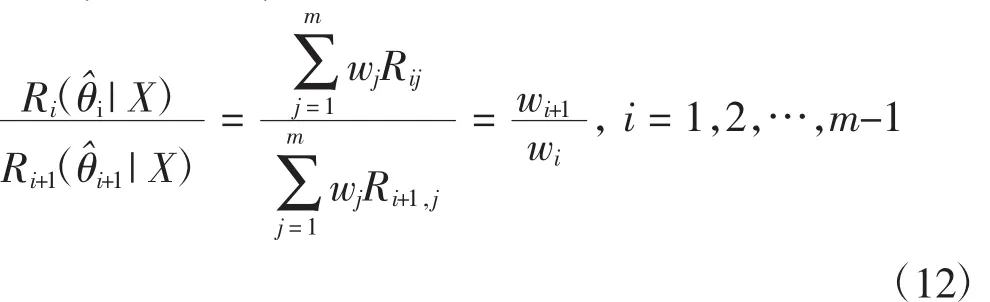
进一步整理（12）式，再结合

得到由m个方程构成的方程组

这是一个非线性方程组，m=2时可直接求解，m≥3时则需运用数值方法（如牛顿迭代法）[10]解出m个权值。

3 数值例

某产品寿命服从正态分布N（θ，1），其中θ为未知参数，并设其真值为10.假定现场抽取8个产品进行定数截尾试验，当失效样本数达到5个时停止试验。从分布N（10，1）中抽取随机数模拟现场试验，得到数据X：8.283 7、9.441 8、9.908 7、10.032 2、10.156 4、10.156 4、10.156 4、10.156 4.现场试验之前已获取两个先验信息，经转化得到两个先验分布，分别是

π1（θ）＝N（9，1）

π2（θ）＝N（12，1）

结合现场数据，在平方损失下，由它们算得的θ估计值依次为9.945 1、10.325 0.计算出后验风险矩阵为

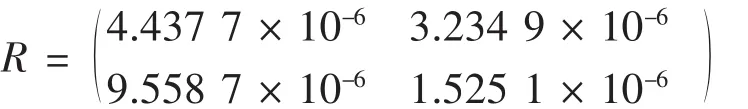
列方程组解得权值

w1＝0.620 8，w2＝0.379 2

再计算出

m1（X）=3.552 6×10-5，m2（X）=1.185 0×10-5

根据（5）式求得融合后验估计

θ赞=10.009 4

与单个先验分布下的估计结果相比，融合后验估计更加接近参数θ的真实值10.

4 结束语

先验信息融合是Bayes理论应用于产品小子样统计评定中的关键环节，也是Bayes理论和可靠性统计领域的持续研究热点。本文针对信息融合过程中的先验分布权重分配问题，提出通过构造后验风险矩阵并基于后验风险与先验分布权重成反比的原则建立起权重求解方程并求得各分布的融合权重，算例验证证实了方法的有效性，为该问题的解决提供了一种新的思路。

[1]张士峰.多源验前信息的融合方法[J].飞行器测控学报，2000，19（1）：26-30.

[2]张金槐.多源信息的Bayes融合精度鉴定方法[J].国防科技大学学报，2001，23（3）：93-97.

[3]张金槐.多种验前信息源情况下的融合验后分布[J].飞行器测控技术，1998，17（3）：28-35.

[4]柴建，师义民，李秀春，等.多源验前信息下的Bayes信息融合方法[J].数理统计与管理，2007，27（3）：308-311.

[5]毛昭勇，宋保维，胡海豹，等.基于分布图信息融合的Bayes可靠性评定方法[J].火力与指挥控制，2010，35（7）：90-93.

[6]刘本纪，龚时雨.Bayesian可靠性评估中多源信息融合的概率模型方法[J].电子产品可靠性与环境试验，2011，29（1）：10-13

[7]侯敏，郭基联，李建伟.多源信息的验前分布融合方法研究[J].火力与指挥控制，2012，37（7）：57-60.

[8]赵仿泽.一种基于D-S证据理论的Bayes可靠性评定方法[J].鱼雷技术，2013，21（3）：175-178.

[9]张尧庭，陈汉峰.贝叶斯统计推断[M].北京：科学出版社，1991.

[10]徐萃薇，孙绳武.计算方法引论[M].北京：高等教育出版社，2002.

Fusion Method for Prior Distributions from Multiple Sources Based on Posterior Risk

CHEN Hong-ke
（Xiamen University Tan Kah Kee College，Zhangzhou Fujian 363105，China）

In order to assign justified weight coefficients for prior distributions from multiple sources in Bayes analysis，a method was proposed based on posterior risk.Posterior risk matrix was constructed in this method and then equations for weight coefficients were established based on the principle that weight of prior distribution being inversely proportional to posterior risk.The given numerical example verified the validity of this method.

information fusion from multiple sources；posterior risk；Bayes；reliability

TB114.3

A

1672-545X（2017）06-0223-03

2017-03-09

陈洪科（1986-），男，讲师，硕士，主要从事产品可靠性、嵌入式系统研究。