孔板流量计内空化现象的数值模拟

谢东梅，张 青，田昭翔，杨雪峰

（四川大学化学工程学院，四川 成都 610065）

孔板流量计内空化现象的数值模拟

谢东梅，张 青，田昭翔，杨雪峰

（四川大学化学工程学院，四川 成都 610065）

以计算流体动力学CFD软件为工具，通过引入Schnerr-Sauer空化模型，并结合多相流Mixture模型与RNG k-ε湍流模型，对两通道非标准孔板流量计在空化发生条件下的内部流场进行数值模拟。考查等效直径比β=0.7时，流场中蒸汽体积分数和压力分布的变化规律，入口压力对空化数的影响以及雷诺数对流出系数和压力损失的影响。结果表明：入口压力增加到一定值时，在环隙边缘处首先发生空化现象，并且随着压力的增大，空化发生的区域增大，空化程度加剧；空化数随入口压力的增大而减小；空化效应对流量计的流出系数的影响较大，而对压力损失的影响较小。研究结果对孔板流量计的测量误差原因分析和提高测量精度有参考价值。

非标准孔板流量计；空化数；压力损失；流出系数；数值模拟

0 引 言

空化是液体所特有的一种复杂的流体动力现象。当流场中某处的局部压力较低时，溶解在液体中的不凝性气体会逸出，当压力降低到对应温度下的饱和蒸汽压时，液体开始汽化，在局部低压下液体中瞬间形成大量空泡，这些空泡随液体流会在低压区时生长、膨胀，而到达高压区时又会收缩、溃灭，这种空泡爆发性生长、膨胀、收缩、溃灭的整个过程称为水力空化现象[1-3]。空化现象的发生有利有弊，目前空化技术成功地运用在工业废水处理，饮用水消毒，选矿等方面[4-7]。在水动力学研究领域，空化普遍出现在核动力系统、低温热交换器、液体火箭发动机等工程领域。当常温流体流经管路、泵、阀门、流量计等各种节流元件时，节流压降容易导致空化的形成与发展[8-9]。空化不仅会使节流元件及下游管道被空蚀损坏、设备效率降低，而且可能导致流量测量不准确、系统运行不稳定。所以，对孔板流量计内流体空化流动特性进行理论与实验研究具有重要的工业实用价值[10-13]。

赵奇等[14]设计的两通道非标准孔板流量计与标准孔板流量计相比，具有临界雷诺数低、永久压降低，测量稳定性高和节能等优势。但没有考虑在入口压力较高或流速较大的情况下，节流元件附近可能发生的空化现象对流量计测量精度会产生影响。本文在其设计的流量计的基础上，研究空化数随入口压力的变化规律以及流出系数和压力损失随雷诺数的变化规律，并讨论空化的发生对孔板流量计测量精度的影响，研究工作对提高测量精度有一定的参考价值。

1 物理模型与数学模型

1.1 几何模型和网格划分

因节流元件为轴对称结构，可简化为二维模拟。本文研究的孔板是根据国家标准GB/T 2624——2006《用安装在圆形截面管道中的差压装置测量满管流体流量》[15]进行设计的，其几何结构如图1所示。管道直径D=100mm，R=50mm，孔板中心孔半径r1=17.5 mm，环孔内半径r2=38.5 mm，环孔外半径r3=49mm，孔板厚度E=3mm，节流孔厚度e=1mm，斜角F=45°，等效直径比β=0.7。孔板上、下游的直管段长度分别取5D和15D。

利用ICEM CFD进行网格划分，如图2所示，整体采用四边形结构化网格，从管道两端到孔板逐渐加密，孔板处进行局部加密，网格总体数量为176262。

1.2 数学模型

采用Schnerr-Sauer空化模型、Mixture模型与RNG k-ε湍流模型联合进行计算。Schnerr-Sauer空化模型的蒸汽输运方程[16]为

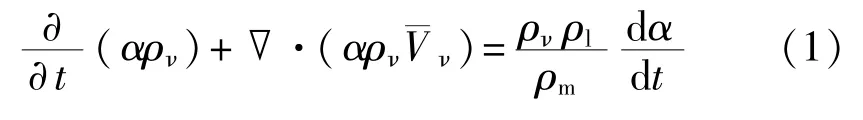
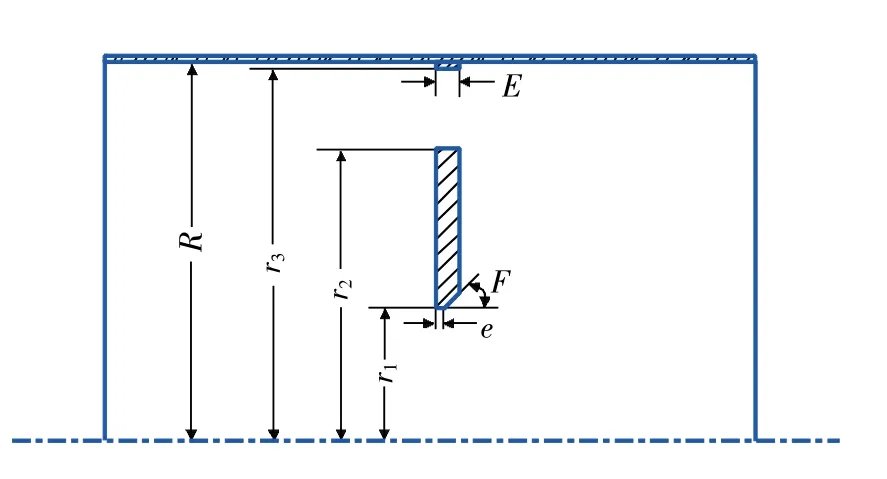
图1 管道结构简图

图2 网格划分图

式中：α——蒸汽的体积分数；

t——时间，s；

ρ——密度，kg/m3；l、v、m分别为液相、蒸汽相、混合相。

净质量源表达式如下：

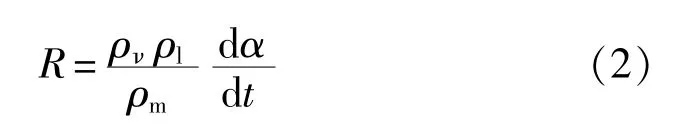
由气泡动力学方程[17]得：

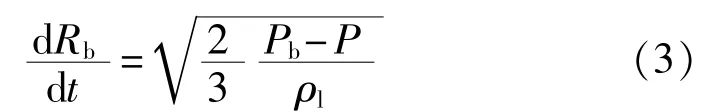
式中：Rb——气泡直径，m；

Pb——气泡表面压力，Pa；

P——局部远场压力，Pa。

蒸汽体积分数和单位液体体积内气泡数量nb的关系如下：

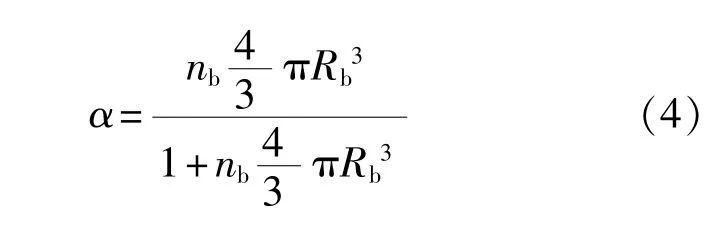
由式（1）～式（4）联立得出式（5）、式（6）如下：

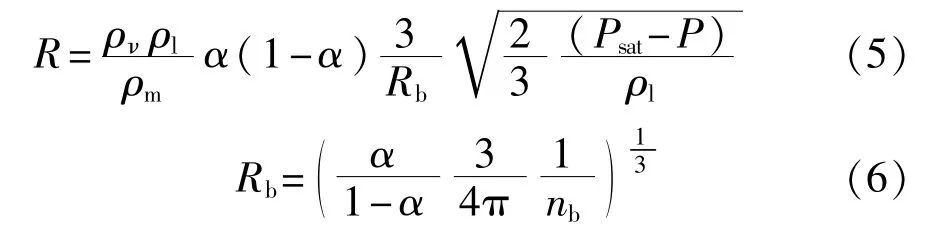
式中：Psat——饱和蒸汽压，Pa；

nb——取单位体积气泡的数量，nb=1×1013/m3。

1.3 模型参数的设置

近壁区域采用Standard wall function，压力-速度耦合项采用SIMPLEC算法，动量和湍流动能采用一阶迎风差分格式。边界条件采用压力入口和压力出口，进口压力的取值范围为 1.01355×105～3.5×105Pa（绝对压力，以下均为绝对压力），出口压力取值为0，操作压强取值为1.01325×105Pa。湍流参数选择湍流强度和水力直径，汽化压强取值3.166×103Pa，液相为常温下的水，气相选择水蒸气。以上各个方程的残差至少达到10-3，保证计算结果充分收敛。

2 数值模拟结果分析

2.1 空化现象数值模拟分析

空化数是描述水力空化和空化状态的一个重要参数，是表征空化特性的无量纲参数。其定义为

式中：P0——孔板下游恢复压力，Pa；

Pv——常温下流体的饱和蒸汽压，Pa；

u0——孔的平均流速，m/s；

ρ——操作温度下流体的密度，kg/m3。

空化数的物理意义为：σ=抑制空化产生的力/促使空化出现的力。理论上讲，只要σ≤1就应该产生空化，σ≤0.5就必然产生稳定的空化。即使在环境压强为几十兆帕时，只要射流速度足够大，就能够出现空化现象。但是，在实际工程应用中发现空化数的离散度较大，用空化数来判断是否产生空化并不准确，所以用空化数判断空化发生没有普遍应用价值。但由于空化数相关参数容易测量、物理意义明确，目前仍是粗略判定空化初生和空化程度的常用方法[18]。

图3所示为模拟得到的空化数随入口压力Pi的变化趋势，空化数随入口压力的增大而减小。实际的空化初生现象一般发生在空化数1.0～2.5之间[2]。

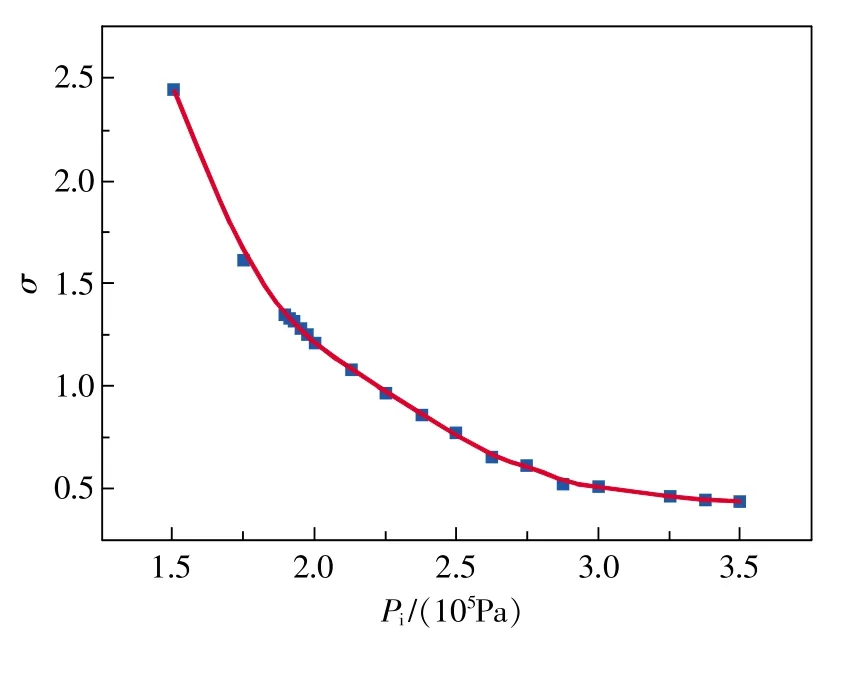
图3 空化数随入口压力的变化曲线

空化初生是空穴在极小区域内初次出现的状态。图4所示为入口压力Pi为1.915×105Pa，入口速度为5.67m/s时，节流孔板前、后区域流体的压力云图。可以看出在节流孔内及孔板后D/2的区域内发生压力骤降，在0.65 m处压力恢复，稳定在1.01×105Pa附近。该压力下首次出现空化现象，由图中数据看出，空化初生时的压力远高于蒸发压力，对应的空化数为 1.33，雷诺数为 5.6×105。

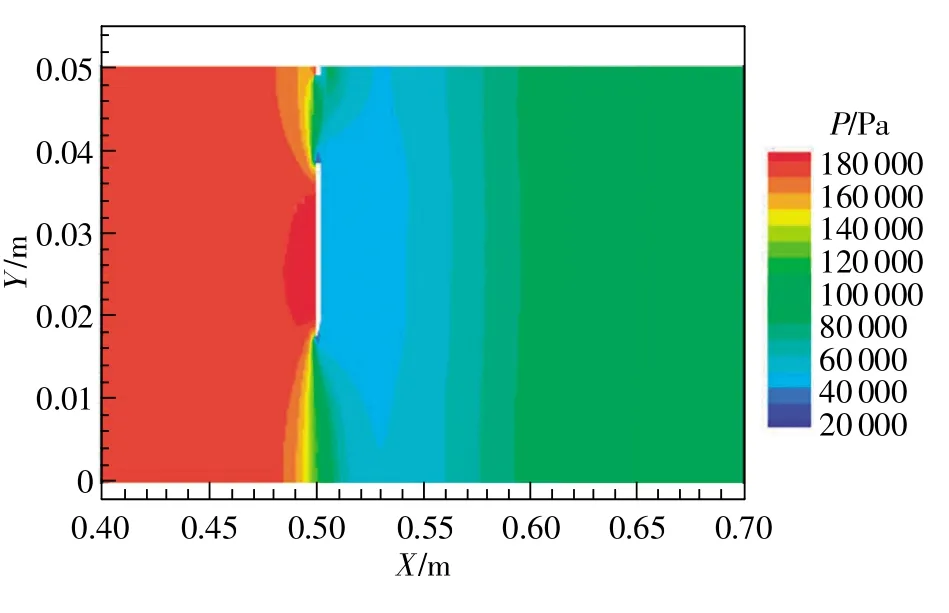
图4 入口压力为1.915×105Pa，入口速度为5.67m/s时的压力分布云图

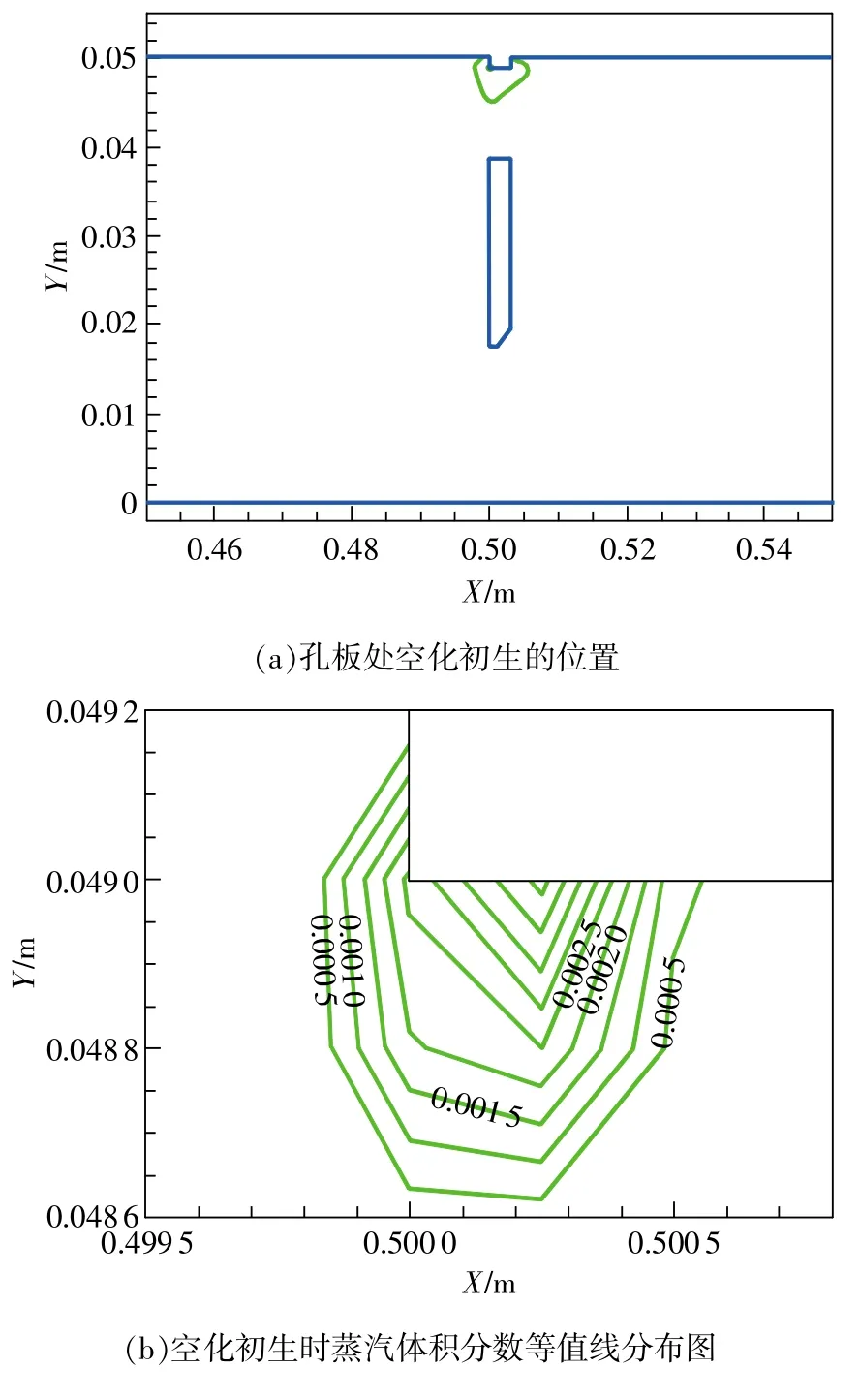
图5 入口压力为1.915×105Pa时，空化初生位置及蒸汽体积分数等值线分布图

图5所示为空化初生时流体中蒸汽体积分数的等值线。从图5（a）可以看出，空化初生出现在孔板上游端面壁面处。图5（b）为发生空化区域的局部放大图，可以看出空化初生是在壁面上开始，在远离壁面处蒸汽体积分数降低。

随着入口压力增加，空化范围越来越大，空化区域内蒸汽体积分数也随着增大，当入口压力Pi为3.5×105Pa，入口速度为8.71m/s时，模拟所得空化数为0.44。如图6所示，可以看出在孔板下游0.3m以内大部分压力区域达到蒸发压力3.166×103Pa，越靠近孔板的地方蒸汽体积分数越高。

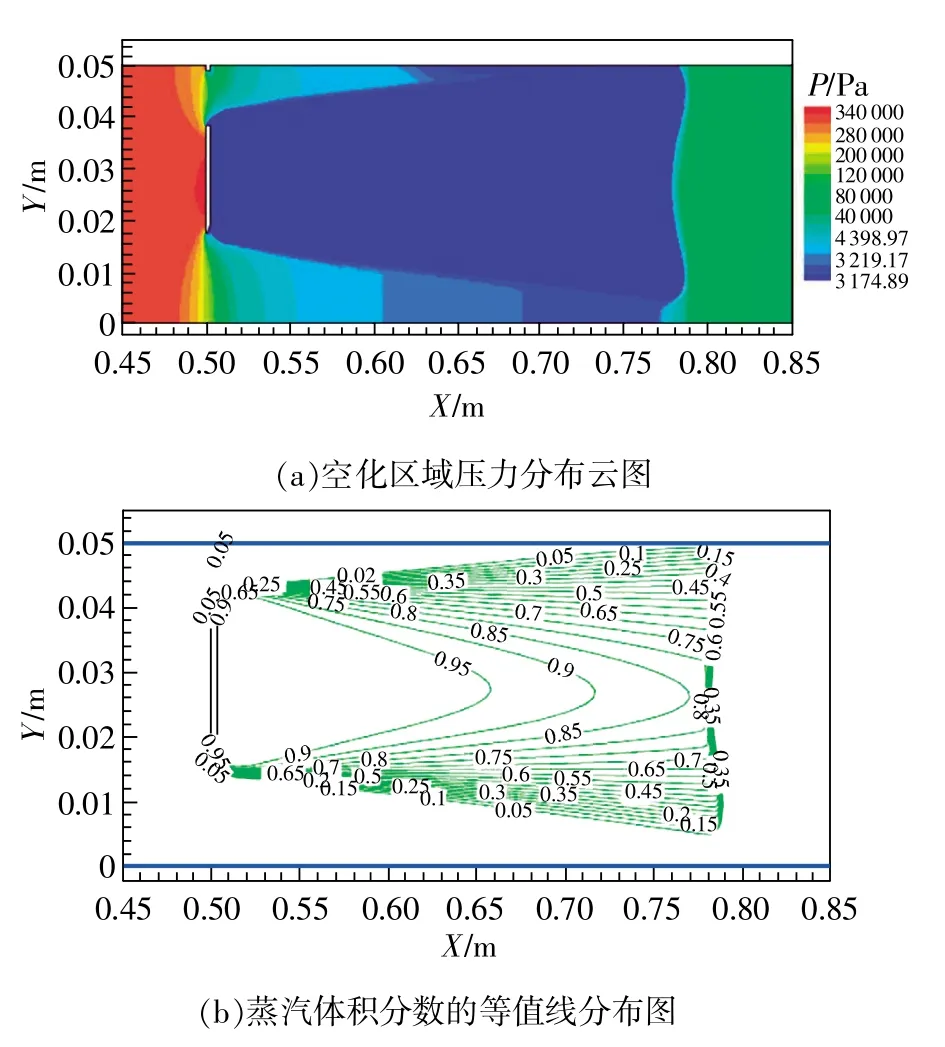
图6 入口压力为3.5×105Pa，入口速度为8.71m/s时的空化区域压力分布和蒸汽体积分数等值线分布图

2.2 空化现象对孔板流量计测量精度的影响

赵奇等[14]开展的模拟研究中没有考虑空化现象对非标准孔板流量计测量的影响，本文通过改变流体的不同入口压力，研究了流出系数C和压力损失Δω随雷诺数Re的变化情况，并对引入空化模型和未引入空化模型的模拟结果进行对比。

雷诺数的计算公式为

式中：u——进口速度，m/s；

μ——流体黏度，Pa·s。

本文通过改变流体的入口压力得到不同的入口速度，计算得到不同状态下的雷诺数。流出系数是通过孔板的实际流量值与理论流量值的比值，是一个统计量，无法实际测出。它与管道的截面积比、取压方式、雷诺数及管道情况等很多因素有关。在选用孔板流量计时，首先应考虑孔板流量计的测量范围位于流出系数为常数的范围内，以保证流量测量的稳定性。

本文通过模拟获得孔板前后的压降，根据下式进行计算，得出流出系数。

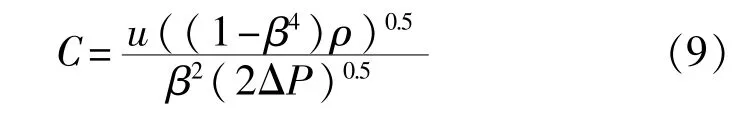
式中：ρ——水的密度，kg/m3；

ΔP——上、下游压差，ΔP=P1-P2；

β——节流比系数。

采用D和D/2取压口取压，上游取压口的间距为L1，L1取0.9D和1.1D之间时无需对流出系数进行校正，本文L1取1D，此处取压P1；下游取压口的距离为 L2，因为 β=0.7，β＞0.6，所以当 L2取 0.49D 和0.51D之间时无需对流出系数进行校正，本文L2取0.5D，此处取压P2。 其中，L1、L2均为从孔板上游端面量起。

图7所示为C随Re的变化关系。可以看出，在两种情况下，C均随Re的增加逐渐减小，并在Re增加到一定值后趋于常数。就工程应用而言，在选用孔板流量计时，应确保它的流出系数落在常数区内。由图 7 可知，应选择 Re 在 1.3×105～7.2×105之间。 Re=5.6×105时，空化初生。还可以看出，在 Re＜7.2×105范围内，引入空化模型的流出系数比未引入空化模型的流出系数大；在Re＞7.2×105时，未引入空化模型的流出系数要大。计算结果表明，在流量计测量过程中，如果流体发生空化现象，则实际流出系数与没有考虑空化效应的原计算值会有偏差，如果仍按原流出系数计算流量，则会引起测量误差。当流体Re在1.3×105～7.2×105范围内，未考虑空化现象的影响，测量值会比实际值偏小。

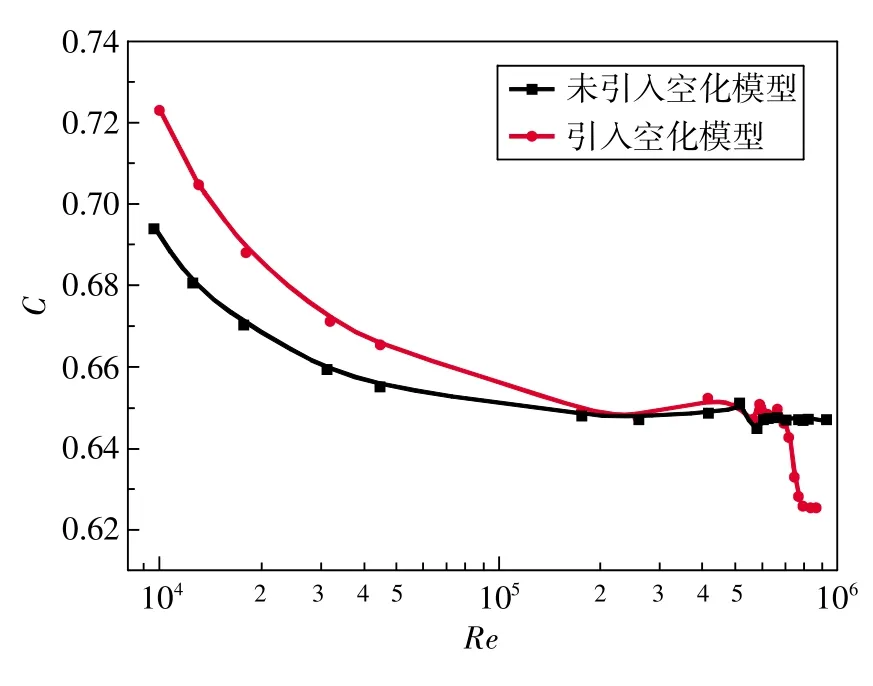
图7 流出系数C随雷诺数的变化曲线

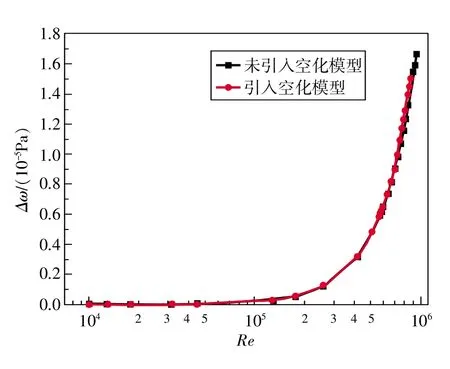
图8 压力损失Δω随雷诺数的变化曲线

永久压力损失是表征装置能量消耗的技术经济指标。压力损失按照GB/T 2624.2——2006的规定进行计算，其公式为

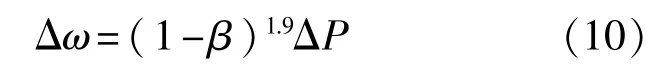
图8所示为两种情况下压力损失Δω与Re的关系。模拟结果表明，在Re＜7.2×105时，引入空化模型的流量计的压力损失小于未引入空化模型的；在Re＞7.2×105时，引入空化模型的流量计的压力损失大于未引入空化模型的。造成此种结果的原因可能如下：在该流量计的流体流动中压力损失表现为静压能转化为内能，该过程中，空化消耗能量为ω1，汽泡的产生使流体与管壁摩擦耗能减少量为ω2。当ω1＞ω2时，表现为压力损失增大，对应 Re＞7.2×105区域；当ω1＜ω2时，表现为压力损失减小，对应 Re＜7.2×105区域。由图可知，虽然空化的发生对流量计的压力损失有影响，但是影响不大。

3 结束语

通过引入空化模型对两通道非标准孔板流量计的流场进行模拟，得出以下结论：

1）随着入口压力的增加，雷诺数逐渐增大，空化数不断减小，在低压下空化数的变化较快，在高压下空化数的变化较慢，说明空化初生现象容易在低压下发生。因此在进行低压、高速的流体测量时更应该注意空化现象的发生。

2）当压力达到一定值时，空化初生发生在孔板的上游端面靠近壁面的凸起处，如果流量计长时间在这样的条件下使用，汽蚀作用有可能造成流量计节流件的磨损，进而影响测量的精度。

3）空化效应对流量计的测量精度有影响，在一定的雷诺数范围内，空化效应会引起流出系数的变化，如果在实际测量时未考虑空化效应的影响，则会造成流量计的测量误差。

[1]WAKESHIMA H.Mechanism of the inception of hydraulic cavitation[J].Journal of Applied Physics，1996（12）：4584-4585.

[2]武君，张晓东.水力空化及应用[J].化学工业与工程，2003，20（6）：387-391.

[3] 林兴华，张敏革.空化射流流场数值模拟的研究进展[J].化工进展，2015，34（4）：921-929.

[4]沈银华，邓松圣.空化射流降解机理研究[J].贵州化工，2007，32（1）：25-27.

[5]徐美娟，王玉恒.多孔孔板水力空化器的优化和应用[J].南开大学学报（自然科学版），2010，43（6）：9-13.

[6]陈利军，吴纯德.水力空化技术在饮用水消毒中的应用[J].水处理技术，2007，33（3）：45-48.

[7]胡勇，张国范.水力空化在氧化锌矿浮选中的应用研究[J].有色金属，2015（2）：25-29.

[8]HAMMITT F G.Cavitation and multiphase flow phenomena[M].New York：McGraw-Hill，1980：147-155.

[9] 黄继汤.空化与空蚀的原理及应用[M].北京：清华大学出版社，1991：47-60.

[10]马富银，杨国平，吴伟蔚.泵的空化现象研究进展[J].流体机械，2011，39（4）：30-34.

[11]段欣悦，厉彦忠.低温流体节流空化现象的形成与发展规律研究[C]//中国制冷协会2009年学术年会论文集，天津：中国制冷学会，2009：1252-1257.

[12]何志霞，陈驭航.多孔孔板水力空化可视化与数值模拟[J].农业机械学报，2016，47（2）：396-401.

[13]余冬梅，卢晓江，李靖.多孔孔板水力空化装置的阻力特性研究[J].轻工机械，2010，28（1）：17-20.

[14]赵奇，牛志娟，杨雪峰.基于CFD的非标准孔板流量计的数值模拟[J].节能技术，2015，33（5）：453-456.

[15]用安装在圆形截面管道中的差压装置测量满管流体流量：GB/2624.2-2006[S].北京：中国标准出版社，2006.

[16]SCHNERR G H，SAUER J.Physical and numerical modeling of unsteady cavitation dynamics [C]//Proceedings of ICMF 2001 International conference on Multiphase Flow，2001：1-8.

[17]BRENNEN C E.Cavitation and bubble dynamics[M].New York： Oxford University Press，1995：79-85.

[18]贺成龙，吴建华，刘文莉.空化应用研究进展综述[J].嘉兴学院学报，2008，20（3）：57-62.

（编辑：李妮）

Numerical simulation of cavitation effect in orifice flowmeter

XIE Dongmei， ZHANG Qin， TIAN Zhaoxiang， YANG Xuefeng
（School of Chemical Engineering，Sichuan University，Chengdu 610065，China）

The internalflow field oftwo-channelnon-standard orifice flowmeterunderthe conditions of cavitation was simulated by using the computational fluid dynamics （CFD） software as the tool，introducing Schnerr-Sauer cavitation model together with the multiphase Mixture model and the RNG k-ε turbulence model.The variations of the vapor volume fraction and the pressure distribution in the flow field， the influence of inlet pressure on the cavitation number， as well as the influence of Reynolds number on the discharge coefficient and pressure loss were investigated for the equivalent diameter ratio β=0.7.The results show that when the inlet pressure increases to a certain value， the cavitation occurs first at the edge of the ring channel.The degree of cavitation is intensified with the increase of the inlet pressure and the area of cavitation increases，the cavitation number decreases with increase of inlet pressure.The cavitation effect demonstrates a stronger influence on the discharge coefficient than on the pressure loss.The simulation results are useful for the error analysis and the improvement of the measurement accuracy of the flowmeter.

non-standard orifice flowmeter； cavitation number； pressure loss； discharge coefficient；numerical simulation

A

1674-5124（2017）06-0129-05

10.11857/j.issn.1674-5124.2017.06.027

2016-12-12；

2017-01-08

谢东梅（1990-），女，山东菏泽市人，硕士研究生，专业方向为化学工程。