基于IMF-SVD包络谱法的轮对轴承故障检测方法研究
2017-07-31刘泽潮
庄 哲,陈 星,施 莹,刘泽潮
(1.西南交通大学 牵引动力国家重点实验室,四川 成都 610031;2.中车青岛四方机车车辆股份有限公司,山东 青岛 266111)
基于IMF-SVD包络谱法的轮对轴承故障检测方法研究
庄 哲1,陈 星2,施 莹1,刘泽潮1
(1.西南交通大学 牵引动力国家重点实验室,四川 成都 610031;2.中车青岛四方机车车辆股份有限公司,山东 青岛 266111)
针对经验模态分解(empirical model decomposition,EMD)所得的本质特征函数(intrinsic model function,IMF)之间存在相互耦合、难以清晰提取高速列车轮对轴承的故障特征问题,提出一种轮对轴承故障检测的新方法。该方法的核心是应用EMD自适应地分解轴承振动信号,得到多尺度的IMF,应用单尺度的IMF信号构造Hankel矩阵,对该矩阵进行奇异值分解(singular value decomposition,SVD),应用奇异值的差分谱来选择其关键奇异值,对关键奇异值进行奇异值重构,通过重构信号的包络谱分析来检测轮对轴承的故障。利用高速列车轮对轴承故障数据对该检测方法和模型进行验证,结果表明:该方法能够清晰地提取表征轴承故障特性的基频、倍频成分,突显故障频率特征,具有一定工程应用前景。
轮对轴承故障;经验模态分解;本质特征函数;奇异值分解;包络检测
0 引 言
轮对轴承是高速列车的核心部件,受到承重载荷、传递载荷和轮轨冲击载荷的联合影响,其工作条件十分恶劣。在列车高速运营条件下,轮对轴承一旦发生故障就会快速发展,若不及时发现故障并采取相应措施,会导致热轴、燃轴、切轴等重特大事故的发生,严重危及行车安全。因此,开展高速列车轮对轴承的故障检测与诊断研究并及时发现轮对轴承故障是十分必要的。
对此,国内外学者开展了广泛而深入的研究,取得了丰硕的研究成果。基于时域统计分析和傅里叶分析的诊断是一种有效的故障检测方法,然而该方法是基于信号为平稳、线性的假设[1]。实际上,因轮对轴承的故障使得轴承元件的冲击超过了材料的线弹性范围而轴承振动信号呈现非线性非平稳的特性[2]。应用傅里叶变换拟合非线性振动需要许多谐波成分,然而这些谐波成分只满足分解的数学关系,而对发现故障没有任何的物理意义[3]。实际情况中轮对轴承故障信号十分微弱,并且在采集时存在大量背景噪声以及信号在传递过程中有变形和失真,使得传统分析方法的运用变得十分困难[4]。为了有效处理非线性非平稳信号,时-频分析得到了充分应用,其中小波变换相对于Wigner-Ville分布而言,因其具有无交叉项,小波函数选择灵活的特点,在轴承、齿轮等故障检测中得到了充分应用[5-7]。但是小波分析不是信号的自适应分析,仅当小波函数的波形特性与信号的波形特性良好匹配时,才能产生高质量的小波分解系数。而EMD是一种自适应的信号处理方法,十分适合处理非线性非平稳信号处理,已经成功应用到机械设备、结构的健康检测中[8-10]。
然而在应用EMD检测高速列车轮对轴承的故障时,发现IMF的包络谱杂乱,难以识别反映轴承故障特性的故障频率,为轮对的故障判定、故障严重性评价带来了一定的困难。深入分析其原因是因为EMD分解同小波分解一样,各尺度的IMF存在频率混叠,存在本质函数的相互耦合。将奇异值理论引入到IMF尺度本质分解信号的再处理中,以消除尺度模式信号的相互耦合效应,清晰地突显轮对轴承的故障特性。
为此,为了充分利用EMD在分析非线性、非平稳信号的独到优势,又合理消除分解模式的耦合效应,将EMD、SVD、包络谱分析有机结合提出一种轮对轴承故障检测的新方法。该方法的核心是应用EMD自适应地分解轴承振动信号,得到多尺度的IMF,应用单尺度的IMF信号构造Hankel矩阵,对该矩阵进行奇异值分解SVD,应用奇异值的差分谱来选择其关键奇异值,对关键奇异值进行奇异值重构,通过重构信号的包络谱分析来检测高速列车轮对轴承的故障。最后应用轮对轴承的故障试验数据对该检测方法和模型进行了试验验证。
1 轮对轴承故障检测IMF-SVD包络法
1.1 EMD分解理论
EMD是由Norden E Huang提出的一种非平稳信号处理的新方法[3]。不像小波变换需要事先确定小波的基函数,它可依据数据自身的时间尺度进行自适应分解,是一种自适应的非平稳数据处理方法。EMD方法对信号x(t)分解步骤如下:
1)确定信号局部极值点,利用三次样条函数插值拟合局部极大值点形成原始数据的上包络线。同样利用三次样条函数插值拟合局部极小值点形成原始数据的下包络线。
2)计算上下包络线的均值 m1(t),信号 x(t)和m1(t)的差值得到新的数据序列为 h1(t):
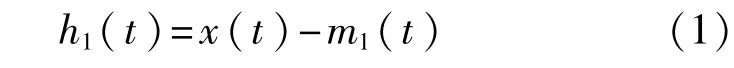
理想地,如果 h1(t)满足 IMF 条件,那么 h1(t)为第1个IMF分量。
3)如果 h1(t)不满足 IMF 条件,则把 h1(t)作为处理信号重复1)和2),重复k次后所得到的平均包络线值趋于零,表示该信号满足了IMF条件,则得到了第1个 IMF 分量记为 c1(t)。
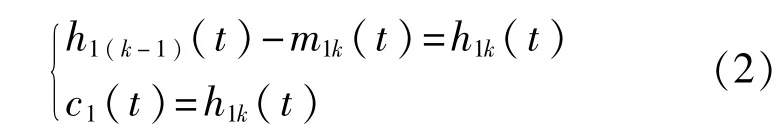
4)第1个IMF分量代表原始数据中的高频成分。用原始序列 x(t)减去第 1 个 IMF 分量 c1(t)得到去掉高频成分的差值序列 r1(t),将 r1(t)作为新的待处理信号重复上面步骤就可以得到第2个IMF分量 c1(t),如此重复直到最后一个差值序列 rn(t)不可再分为止,rn(t)代表原始序列的均值和趋势。
通过 1)~4)的分析处理,数据序列 x(t)就被分解为n个IMF分量和一个均值或趋势项rn(t),这相当于一个对信号筛选的过程。

式中,各个固有模态函数 IMF,c1(t),c2(t),…,cn(t)包括了从高频到低频的不同频段的分解信号,其频率段均不同并且随着x(t)的不同而改变。但是IMF之间存在的耦合效应、频率混叠效应使得其包络谱较为杂乱,无法清晰地辨识出轮轴的故障特征,为此将奇异值理论引入到IMF的再分析中。
1.2 奇异值分解与重构理论
SVD分解是线性代数中一种重要的矩阵分解,是矩阵分析中正规矩阵酉对角化的推广[11]。奇异值分解运用于信号的分解和特征提取具有特别的优势,奇异值对信号消噪的结果具有零相移、波形失真小、信噪比高等优点,十分适合消除信号的耦合效应和噪声干扰[12-13]。
设矩阵 A∈Rm×n,则存在正交矩阵 U∈Rm×m和正交矩阵 V∈Rn×n,使得:

则式(4)称为矩阵A的奇异值分解。其中:
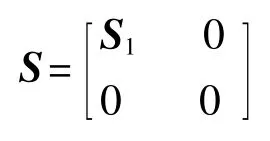
S1=diag(σ1,σ2,…,σr),其对角元素按照顺序排列 σ1≥σ2≥…≥σr,r=rank(A)。
利用奇异值分解理论进行信号处理时,需要利用单尺度IMF构造Hankel矩阵A[14]。
为了实现奇异值的重构,将式(4)改写为向量ui和向量vi的表达形式:
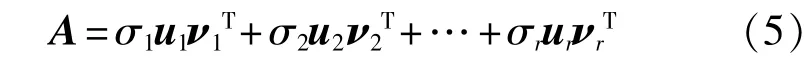
式中ui∈Rm×1是矩阵A奇异值分解结果的左正交矩阵的列向量。vi∈Rn×1是矩阵A奇异值分解结果的右正交矩阵的列向量,σi是矩阵A奇异值分解结果的奇异值。 若令 Ai=σiuiviT,Ai∈Rm×n,则矩阵 Ai中的数据排列为

取矩阵 Ai的第 1 行向量元素 Pi,1=(xi,1,xi,2,…,xi,n),取矩阵Ai的最后一列的列向量(除去向量中的第1个元素)Li,n=(xi,n+1,xi,n+2,…,xi,N),比较 Hankel矩阵各元素间排列顺序,将Hankel矩阵的 Pi,1和 Li,n首尾相接,就构成了一个分量信号 Pi=(Pi,1,LTi,n)。
每一个Ai所对应的Pi都是对分析信号x(t)的一个奇异值分解后的重构。 Ai(i=1,2,…,r)中的 Pi线性叠加实现被分原始信号的重构:
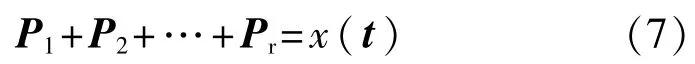
1.3 奇异值选择
奇异值越大对信号矩阵贡献越大。通过Hankel矩阵的构造方式可以知道对于有用信号在矩阵中行与行之间出现一位的错位,行与行之间高度相关使得矩阵高度病态,病态矩阵的秩r远远小于q=min(m,n)。而对于噪声信号而言,行与行之间也仅仅相差一个数据,但是噪声信号各个值之间完全不相关,这样构造的噪声矩阵是一个满秩的良性矩阵,其奇异值分解结果分布均匀,都不为零。本论文通过仿真信号对此进行说明,构造以下信号 sin(3t)+sin(20t)+ξ(t),ξ(t)为均值为0方差为1的白噪声,在分别构造该组信号中的交流信号与噪声信号,在[0,2π]内采样512个点。构造各个信号的Hankel矩阵,其奇异值分解结果如图1所示。
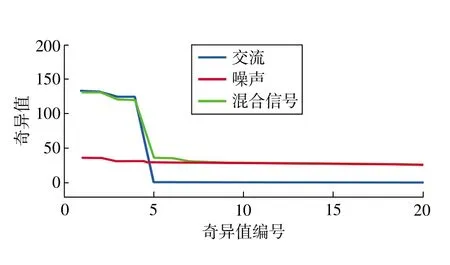
图1 信号奇异值的分布
由图可得,交流信号的奇异值主要集中在前4个奇异值,而后面的奇异值几乎为0。噪声信号奇异值分布均匀,均不为0。混合信号的奇异值分布是两个分量信号奇异值结果的叠加,有用信号集中在前4个奇异值,后面平坦部分均为噪声相关的奇异值。
信号时域图形和加入噪声后的时域图形分别如图2、图3所示,用含有噪声的信号来构造Hankel矩阵,进行奇异值分解,选取前4个奇异值进行重构得到的重构信号如图4所示。
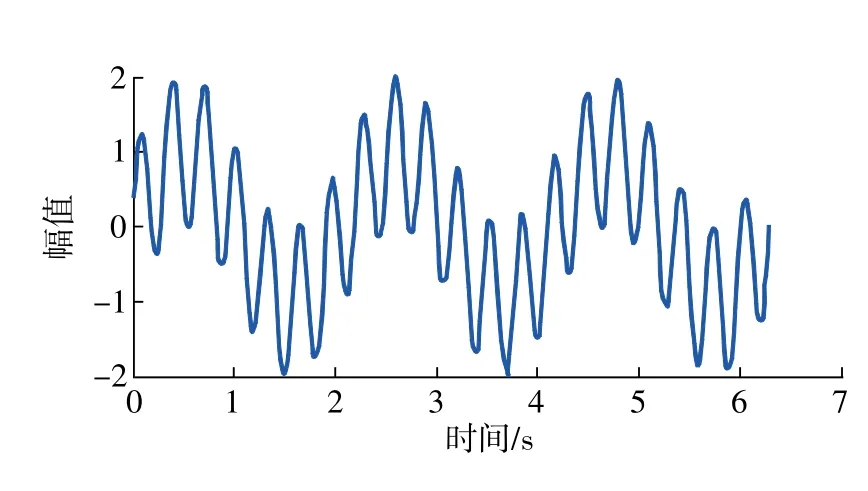
图2 原始信号图
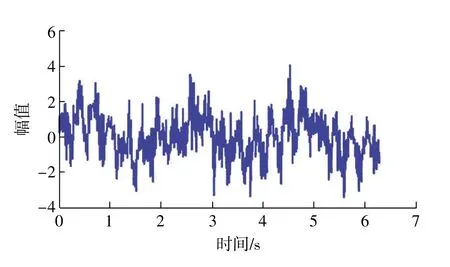
图3 含噪信号
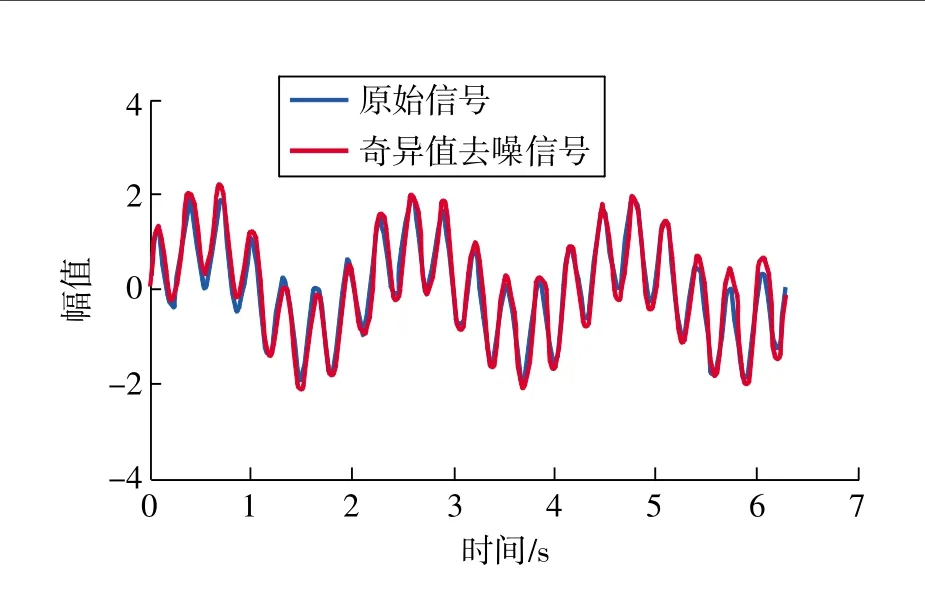
图4 原始信号和重构信号对比
本论文采用奇异值差分谱为奇异值的选择依据[13],计算两个奇异值的差值 bk=σk-σk+1,根据两个奇异值之间差值的大小评判奇异值变化的大小(矩阵奇异值分解的时候,有用信号大多集中较大的前几个奇异值上,而噪声信号的奇异值基本比较小并且之间变化不大,所以噪声信号的奇异值之间差值最小),当有用信号向噪声信号的奇异值变化时,会出现差值的峰值。该点前面的奇异值是有用信号的奇异值。
2 轮对轴承故障检测模型
检测模型如图5所示。
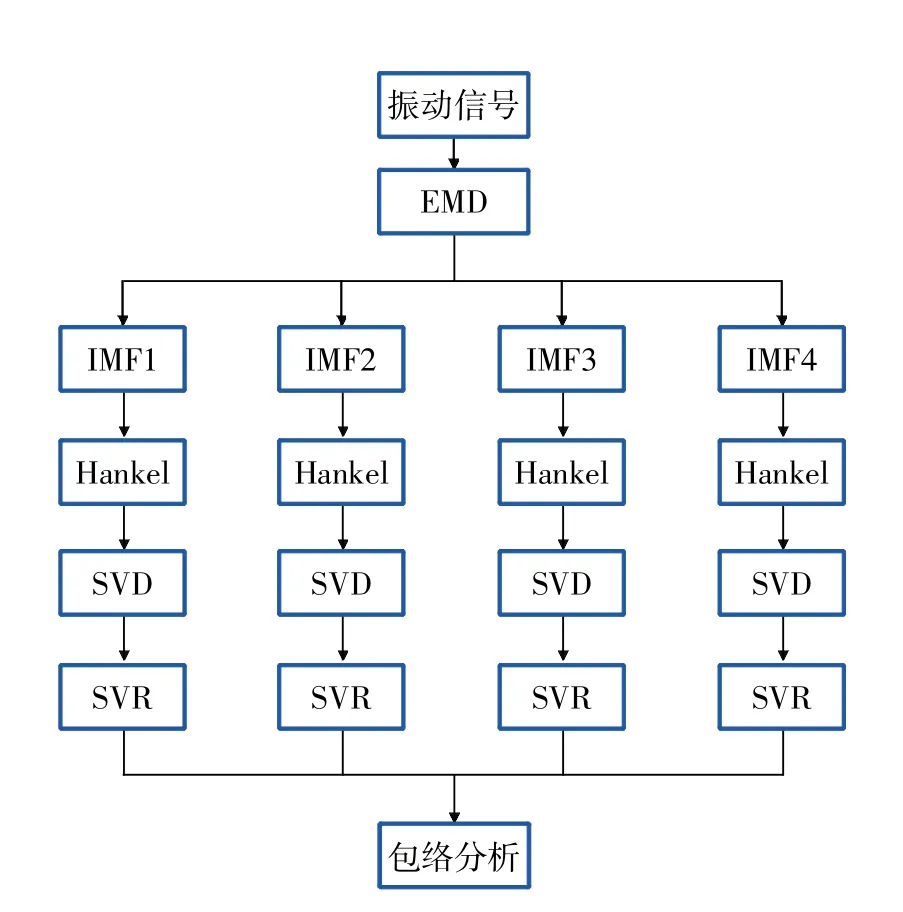
图5 轴承故障检测模型
对轴承振动信号进行EMD分解,得到多尺度的分解信号IMF,对单尺度信号构造Hankel矩阵,对矩阵进行奇异值分解与重构,对重构信号进行包络解调分析,通过包络谱来检测轮对轴承的故障特性。

图6 轮对轴承故障试验台

图7 轴承外圈人工伤故障
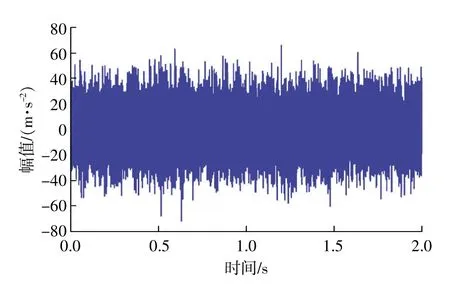
图8 故障试验数据
3 检测模型的试验验证
建立轮对轴承故障试验台,如图6所示。主要包括驱动轮、轮对和加载装置,将人工伤轴承安装在该试验台上做故障试验,轴承的故障如图7所示。在转速n=925r/min获取故障振动数据,具体如图8所示。
依据轴承几何参数、转速可计算轴承内、外圈故障频率,轴承内圈旋转频率:

其中n=925r/min为轴承转速。
轴承滚动体通过外圈一点的频率:
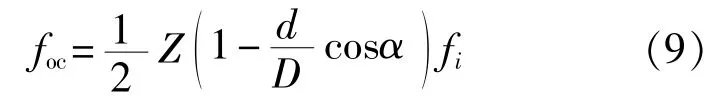
式中:Z——滚动体个数,Z=19;
d——滚动体直径,d=27mm;
D——轴承节径,D=180mm;
α——压力角,α=9°。
具体的故障频率如表1所示。

表1 轴承的主要故障频率
对图8中所示的振动信号做EMD分解并对第一尺度IMF做包络谱分析,如图9所示。图中谱线非常丰富和杂乱,很难发现特征频率,这样做故障诊断很容易出现误判和误诊。

图9 IMF1包络谱
为了实现精确的诊断,对第一模态函数做奇异值分解,并计算奇异值差分谱,奇异值差分谱的每一个拐点都是频率突变点,这些突变点反应轴承故障冲击。根据差分谱突变点的大小,选取前16个奇异值做奇异值重构并计算其包络谱,得到图10所示。
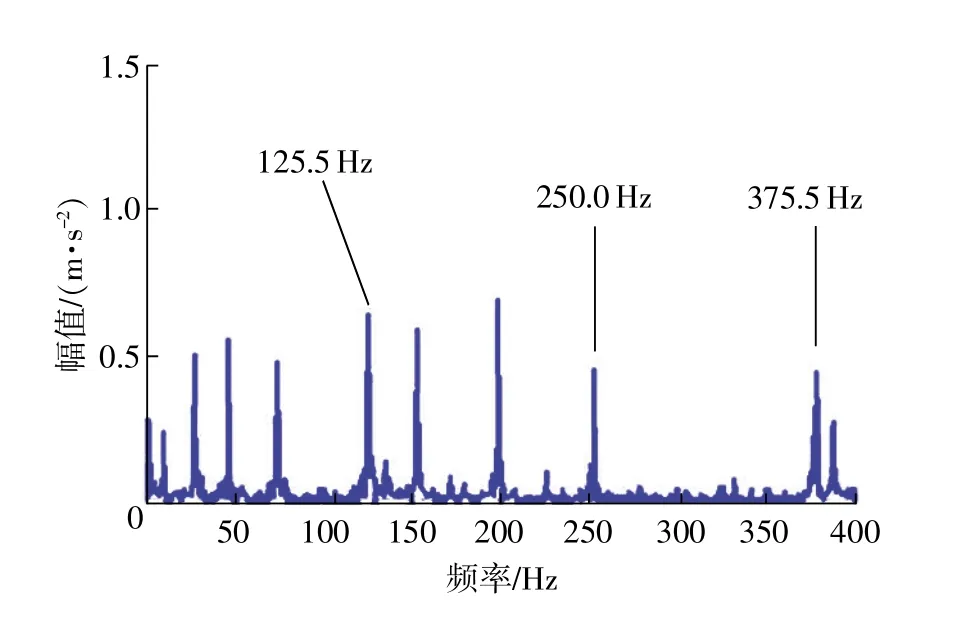
图10 IMF1-SVD包络谱
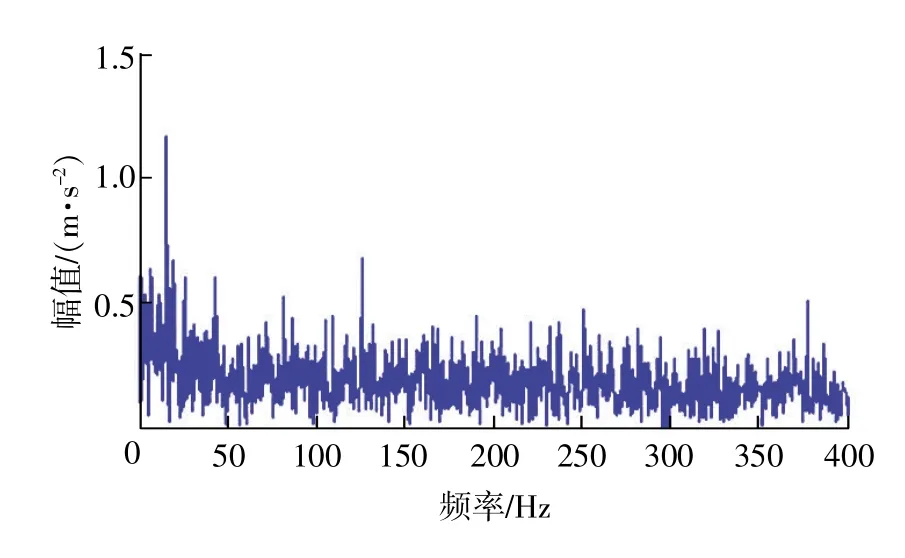
图11 IMF2包络谱
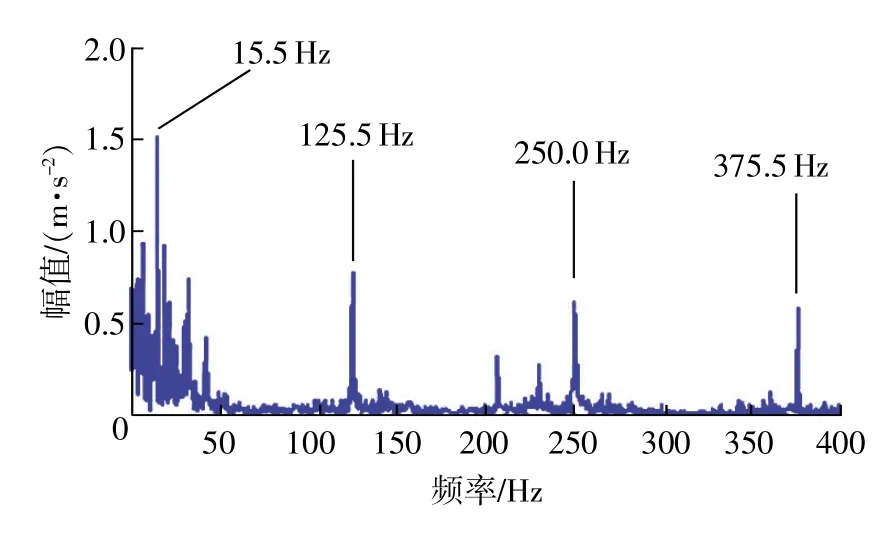
图12 IMF2-SVD包络谱
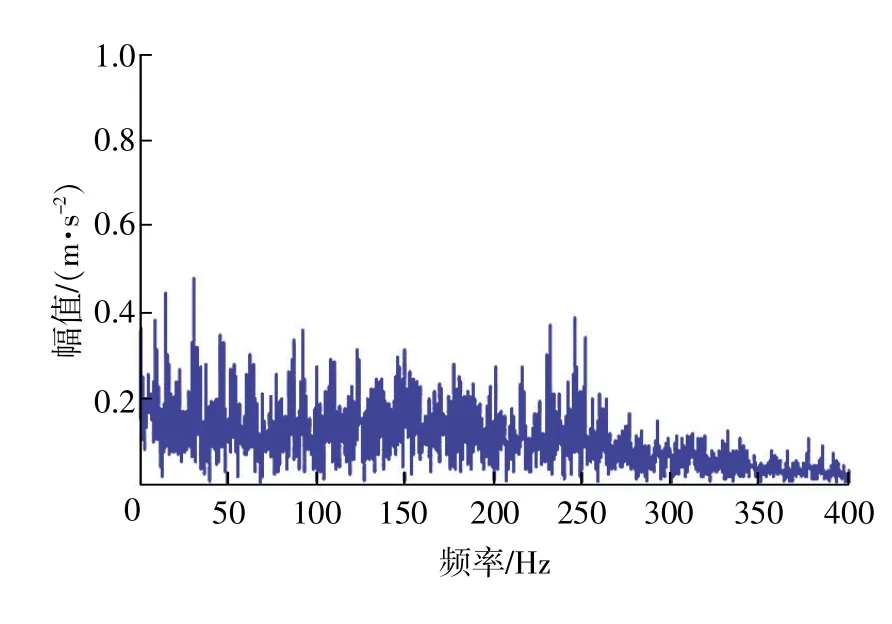
图13 IMF3包络谱
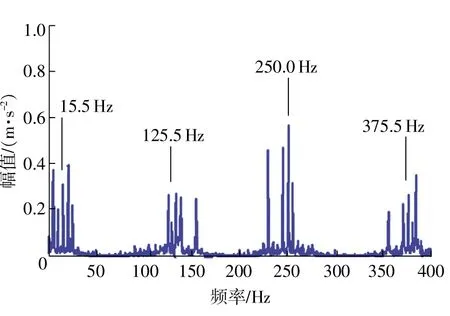
图14 IMF3-SVD包络谱
将图10与图9比较可以看出,特征频率较为清晰,能够检测出轴承的故障。同理对第2个IMF做包络谱分析(如图11所示)。图中谱线也非常丰富和杂乱,很难发现特征频率。对第2个IMF做IMFSVD-包络分析,如图12所示(根据差分谱突变点的大小,选取前60个奇异值做奇异值重构并计算其包络谱),图中可以发现谱线比图11中的更加清晰和干净,并且能准确找到故障特征频率和转频。
最后对第3个IMF做包络谱分析(如图13所示),对该信号做奇异值分解,并计算奇异值差分谱,选取前14个奇异值做奇异值重构并计算其包络谱,如图14所示。同前两个模态分量一样都能准确找到轴承故障的特征信号。验证了这一故障诊断模型的可行性和准确性。
通过对各个尺度的IMF包络谱和IMF-SVD包络谱的对比可以看出,此方法能够有效捕捉轴承的故障频率,谱的清晰度较高,验证了该方法的有效性。但是需要指出的是关系轴承故障频率以外其它频率的物理意义还不明确,目前正在建立轴承试验系统的动力学模型,分析其振动形成机理。
4 结束语
通过EMD、SVD、包络谱分析的有机结合,实现轮对轴承的故障频率检测技术概括起来具有以下特点:
1)充分利用了EMD处理非线性非平稳信号的自适应尺度划分特性,充分利用了奇异值分解对消除噪声和信号耦合干扰的独特优势。
2)两种方法的结合提高了各个尺度包络谱的清晰度,有力的突显了故障频率特征。
3)该方法能够捕捉到轮对轴承的转频、故障的基频、倍频等故障特征,具有一定工程应用前景。
[1]YANG C Y,WU T Y.Diagnostics of gear deterioration using EEMD approach and PCA process[J].Measurement,2015(61):75-87.
[2]LOUTRIDIS S J.Damage detection in gear systems using empirical mode decompo-sition[J].Engineering,2004(26):1833-1841.
[3]HUANG N E, SHEN Z, LONG S R.The Empirical mode decomposition and the Hilbertspectrum for nonlinear and non-stationary time series analysis[J].Proceedings of the Royal Society of London,1998(454):903-995.
[4] 王晗,何刘.最小熵解卷积法轮对轴承故障诊断[J].中国测试,2016,42(1):114-120.
[5]SU W, WANG F, ZHU H, et al.Rolling element bearing faults diagnosis based on optimal Morlet wavelet filter and auto-correlation enhancement[J].Mechanical Systems&Signal Processing,2010,24(5):1458-1472.
[6]CHENG J S, YU D J, YANG Y.Application of an impulse response wavelet to fault diagnosis of rolling bearings[J].Mechanical Systems&Signal Processing,2007,21(2):920-929.
[7] 荣少巍.基于小波变换的磁悬浮直线电机故障诊断研究[J].电子测量技术,2014,37(11):109-112.
[8]ZHAO X, PATEL T H, ZUO M J.Multivariate EMD and full spectrum based condition monitoring for rotating machinery[J].Mechanical Systems&Signal Processing,2012,27(1):712-728.
[9]WU T Y, CHUNG Y L.Misalignment diagnosis of rotatingmachinerythrough vibration analysisvia the hybrid EEMD and EMD approach[J].Smart Materials&Structures,2009,18(9):7566-7579.
[10]孙文军,芮国胜,张弛,等.机械故障的级联共振和EMD联合参数辨识方法[J].电子测量与仪器学报,2016,30(3):352-360.
[11]LEHTOLA L,KARSIKAS M,KOSKINEN M,et al.Effect of noise and filtering on SVD-based morphological parameters of the T wave in the ECG[J].Journal of Medical Engineering&Technology,2008,32(5):400-407.
[12]MAJ J B, ROYACKERS L, MOONEN M, et al.SVD-based optimalfiltering fornoise reduction in dual microphone hearing aids:a real time implementation and oerceptual evaluation[J].IEEE Transactions on Biomedical Engineering,2005,52(9):1563-1573.
[13]赵学智,陈统坚,叶邦彦,等.基于奇异值分解的铣削力信号处理与铣床状态信息分离[J].机械工程学报,2007,43(6):169-174.
[14]丁建明,林建辉,王晗,等.万向轴动不平衡检测的二代小波变换奇异值方法[J].机械工程学报,2014,50(12):110-117.
(编辑:刘杨)
Research on fault detection of wheel set bearing based on IMF-SVD envelop spectrum method
ZHUANG Zhe1, CHEN Xing2, SHI Ying1, LIU Zechao1
(1.State Key Laboratory of Traction Power,Southwest Jiaotong University,Chengdu 610031,China;2.CRRC Qingdao Sifang Co.,Ltd.,Qingdao 266111,China)
A new method of detecting wheel set bearing fault is proposed aiming at the adverse influence that the inter coupling between each IMF obtained based on the EMD and the problem that hard to clearly extract characteristic of wheel set bearing fault.The core of the method is to obtain multi-scale IMFs through the self-adaptive decomposition bearing vibration signal of EMD,construct the Hankel matrix by using single-scale IMF and carry out SVD for the matrix.The crucial singular values were selected based on the differential spectrum of singular values to reconstruct the crucial single scale.The envelope spectrum analysis of reconstruction signal is employed to detect the fault of wheel set bearing.The detection theory and model is verified through a lot of fault experiment data of wheel set bearing of high-speed train.The result shows that the method developed in this paper can distinctly draw the fault features,and the basic frequency and multi frequency of fault characteristic of representation bearing can be clearly extracted, which effectively reflect the fault frequency characteristics, and has a certain prospect in engineering application.
fault of wheel set bearing; EMD; IMF; SVD; envelope spectrum detection
A
1674-5124(2017)06-0093-06
10.11857/j.issn.1674-5124.2017.06.020
2016-10-18;
2016-12-12
四川省科技计划项目(2016JY0047)
庄 哲(1987-),男,山东临沂市人,博士研究生,主要从事车辆故障诊断及弓网耦合方面研究。
