接触爆炸荷载作用下溢流坝的抗爆性能＊

徐 强，曹 阳，陈健云

（1．大连理工大学海岸与近海工程国家重点实验室，辽宁大连116024；2．大连理工大学建设工程学部水利工程学院工程抗震研究所，辽宁大连116024）

接触爆炸荷载作用下溢流坝的抗爆性能＊

徐 强1，2，曹 阳1，2，陈健云1，2

（1．大连理工大学海岸与近海工程国家重点实验室，辽宁大连116024；2．大连理工大学建设工程学部水利工程学院工程抗震研究所，辽宁大连116024）

以黄登重力坝的溢流坝为研究背景，考虑混凝土的高应变率效应，运用Lagrange－Euler耦合算法建立大坝－库水－空气－炸药全耦合数值模型，研究溢流坝在接触爆炸荷载作用下的抗爆性能。分析满库与空库时溢流坝在爆炸冲击波作用下的动力响应及损伤程度，并进一步研究满库时大坝在不同炸点的水下接触爆炸荷载作用下的动力响应及损伤分布。研究结果表明，满库时水下爆炸比空库时爆炸的动力响应及损伤程度大得多；溢流坝的抗爆薄弱部位主要集中在溢流道顶部及坝体上游折坡处。研究溢流坝的抗爆性能时应重点研究满库时水下爆炸对大坝的破坏特性。

溢流坝；接触爆炸；动力响应；损伤；抗爆性能

恐怖活动已成为当今国际社会安全的重大威胁，其中最常见的恐怖袭击就是爆炸［1］。因此，在爆炸荷载作用下工程结构的防护安全已成为工程结构防护领域的重中之重［25］。随着国民经济的发展，中国的水电事业进入快速发展阶段，一大批水工大坝已建或正在兴建。水工大坝作为国民经济建设中一类重要的工程结构，具有显著的社会、经济和政治效益，因此，关于其抗爆性能的研究日益引起研究者的关注。水工大坝一旦遭到恐怖袭击，将给国家和人民带来巨大的灾难和损失。因此，研究爆炸荷载作用下大坝的抗爆性能对大坝工程结构的安全防护具有十分重要的理论与实际意义。

爆炸荷载作用下大坝的动力响应是一个复杂的物理过程，包括炸药的起爆过程、爆炸冲击波在介质中的传播过程、介质与结构相互作用及结构响应4个过程。目前，对于爆炸荷载作用下的大坝的动力响应及抗爆性能的研究，主要集中在数值模拟研究以及较少的模型实验研究。在数值模拟研究中，李鸿波等［6］和薛新华等［7］采用简化爆炸的前3个物理过程的方法，将爆炸荷载简化为某种已知的荷载函数施加在结构上，不考虑大坝、库水、地基的耦合过程，分析大坝的动力响应及损伤过程；鉴于简化荷载造成的不准确性，徐俊祥等［8］通过建立大坝、库水、空气、炸药以及地基全耦合数值模型，分析爆炸荷载作用下大坝动力响应的复杂物理过程；T．T．Yu［9］运用LS－DYNA建立了混凝土重力坝挡水坝段的水下爆炸全耦合数值模型，分析大坝的损伤演变及压力波传播过程；张社荣等［1013］对混凝土重力坝挡水坝段的水下爆炸进行了数值模拟，探讨了不同水位、不同爆心距、不同起爆深度及不同药量对大坝抗爆性能的影响；李本平［14］利用任意Lagrange－Euler耦合计算方法，对炸弹连续打击混凝土重力坝进行了数值模拟，研究了大坝的破坏效应；张社荣等［15］通过建立高拱坝整体全耦合模型，对水下爆炸荷载下拱坝的动力响应进行了分析。对于爆炸荷载作用下大坝的动力响应实验研究，陆路等［16］采用落锤冲击方法，对水下核爆的一次冲击波作用下混凝土重力坝挡水坝段的动力响应进行了模拟。由于爆炸过程的复杂性，对爆炸荷载作用下大坝的抗爆性能研究主要集中在重力坝的挡水坝段及拱坝。重力坝的溢流坝作为整个重力坝中抗爆性能较薄弱的部位，目前对重力坝溢流坝抗爆性能的报道则较少。

本文中，运用显式非线性动力程序AUTODYN建立大坝、库水、空气和炸药全耦合数值模型，并考虑混凝土的高应变率效应［1718］，研究浅水爆炸荷载作用下混凝土重力坝溢流坝的抗爆性能。通过比较满库与空库时溢流坝水下接触爆炸荷载作用下的动力响应和损伤过程，得到满库条件下不同炸点深度时溢流坝动力响应及损伤分布的变化规律，以期为混凝土重力坝的溢流坝抗爆安全评估和抗爆防护设计提供参考。

1 混凝土动力损伤模型

混凝土材料在爆炸冲击荷载作用下的动态响应非常复杂，其应变表现出非常明显的率相关性。针对高速冲击下混凝土的率相关性，Riedel等提出了Riedel－Hiermaier－Thoma（RHT）本构模型。该模型是在HJC本构模型基础上发展演变而来的，与HJC模型不同的是，RHT引入了弹性极限面、失效面和残余失效面等3个极限面，分别用于表示混凝土的初始屈服强度、失效强度和残余强度的变化规律。

RHT混凝土本构模型在考虑混凝土的高应变率、大应变、高压效应的同时，兼顾了应变硬化、软化和应力偏量第三不变量的影响，可以有效地描述混凝土从弹性到失效的整个过程，因而该模型已被广泛用于模拟爆炸冲击等高应变率动力加载下混凝土动力响应和损伤断裂问题的研究。RHT混凝土本构模型如图1所示。

AUTODYN中自带的材料库中包含了RHT混凝土本构模型。为尽量符合我国混凝土规范和计算模拟的准确性要求，本文中采用修正过的RHT混凝土本构模型参数［1921］，如表1所示。其中A和N分别为失效面常数和失效面指数，p＊spall为归一化的层裂强度，Q0为拉压子午比，BQ为脆性韧性转变参数，B和M 分别为与残余失效面有关的常数和指数，εfmin为最小失效应变，σPTF为主拉伸失效应力。其余参数为AUTODYN材料库中默认的RHT本构模型参数。

图1 RHT本构模型Fig．1 RHT consititute model

表1 修正的RHT本构模型参数Table 1 Modified parameters of RHT constitutive model

2 材料模型及状态方程

2．1 空气模型

假定空气为理想气体，其状态方程为：

式中：pg为气体压力；γ为比热比，取值为1．4；ρg为空气的当前密度；ρ0为初始时刻的空气密度，并且ρ0＝1．225kg／m3；E为气体体积内能，空气的初始能量密度E0＝2．068×105J／g。

2．2 水模型

水采用Grüneisen多项式状态方程。对于流体，在压缩和膨胀状态下其状态方程的表达式不同。

当水压缩（μ＞0）时，其状态方程为：

当水膨胀（μ＜0）时，其状态方程为：

式中：pw为水中的压力；ρ0为水的密度，取998kg／m3；μ为压缩比，μ＝ρ／ρ0－1；ew为水的内能，考虑到静水压力的影响，129m水深时，初始内能为5．642J／kg；此外，A1＝2．2×106kPa，A2＝9．54×106kPa，A3＝1．457×107kPa，B0＝B1＝0．28，T1＝2．2×106kPa，T2＝0。

2．3 炸药模型

TNT炸药采用JWL状态方程，即：

式中：Ae、Be、R1、R2、ω为材料参数，参数取值为：Ae＝373．77GPa，Be＝3．75GPa，R1＝4．15，R2＝0．9，ω＝0．35；pe为压力；V为相对体积；ee为炸药的体积内能。炸药计算参数为：炸药密度为1 630kg／m3，爆轰速度为6 930m／s，C－J压力为21GPa，ee＝3．68×106J／kg。

3 有限元计算模型

水下爆炸过程涉及爆炸产物、水以及周围空气的膨胀和坝体的破坏损伤，因此在计算过程中要有效地处理材料的大变形及损伤。Lagrange算法是以物质坐标为基础，能够对结构的边界运动进行精确的描述，但是当涉及大变形问题时，由于算法本身特点的局限性，将会出现网格畸变等严重的问题，不利于有限元计算的进行。Euler算法是以空间坐标为基础，可以避免网格的畸变问题，能够模拟爆炸产物的大变形流动，但是在描述固体材料的物质边界时较困难。本文结合Lagrange算法与Euler算法各自的优点，采用Lagrange－Euler耦合算法［2225］，该算法的可行性在文献［19］中已经得到验证。

有限元模型以黄登重力坝为背景，选取该重力坝的一个溢流坝段为研究对象，考虑到溢流道的对称性，建立1／2计算模型。大坝坝高为159m，坝底宽度为132．5m，库水深度为129m，坝段宽度为17．5m，溢流道半宽为7．5m，导流墙宽度为5m。如图2所示，全耦合模型包括大坝、库水、空气和TNT炸药，其中大坝混凝土采用Lagrange算法，单元数量为104 142，其他材料采用Euler算法，网格单元数量为139 125。为了讨论浅水爆炸荷载作用下大坝的动力响应及损伤，分别在大坝上游面水下10m（炸点1）、20m（炸点2）以及30m（炸点3）位置处布置炸点。炸药网格尺寸设为1．0m×1．0m×0．5m；TNT药量为815kg，相当于文献［14］中某导弹装药量的2～3倍。在溢流道及坝顶导流墙设置测点（测点1和测点2，如图2所示）。测点1设置在导流墙与溢洪道的相交线上，这是导流墙结构的薄弱处，此处可以监测溢流道与导流墙的动力响应，并为导流墙与溢流道的坍塌破坏提供数值依据；测点2设置在导流墙顶部，此位置安装有泄洪闸门与启闭机。闸门槽在爆炸荷载作用下的动力响应大小直接关系到闸门安全运行的可靠性，因此导流墙顶部动力响应的研究对溢流坝坝顶的机电设备和结构防护有重要的实际意义。

边界条件设置：考虑到溢流道的对称性，在1／2模型的对称面上施加对称边界，以模拟整个溢流道爆炸损伤效果。溢流坝坝体的外表面施加Transmit边界条件（适用于Lagrange算法），模拟无限长的坝段；空气与库水的外四周施加Flow＿out边界条件（适用于Euler算法），以模拟无限的空气与库水。本文中不考虑地基对坝体的影响，在大坝底部施加全约束。

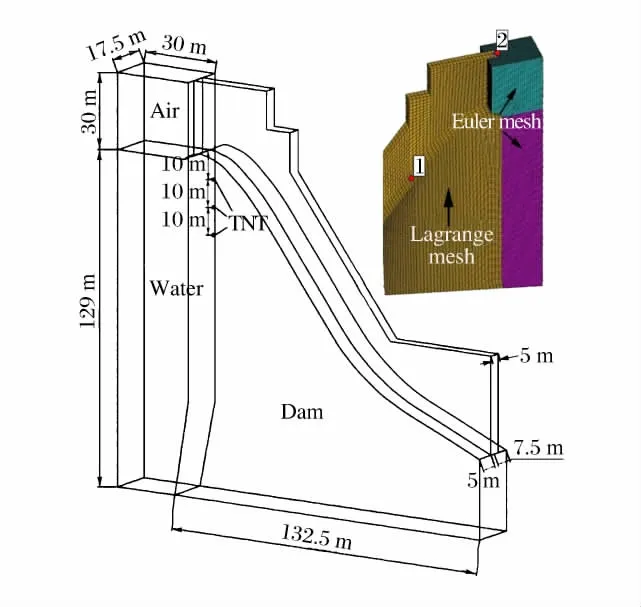
图2 溢流坝全耦合模型Fig．2 Coupled model of overflow dam

4 满库与空库条件下溢流坝的抗爆性能

以在炸点2位置爆炸工况为研究对象，分析满库与空库条件下溢流坝在爆炸荷载作用下的响应行为，分别从加速度、速度和位移时程曲线及损伤分布情况研究溢流坝的抗爆性能。

图3给出了在炸点2处爆炸时满库与空库条件下测点1与测点2的位移、速度及加速度时程曲线。由图3（a）可知，随着时间的增加，测点1与测点2的位移沿着顺河向均不断增大，满库时的位移幅值远大于空库时的位移幅值。由图3（b）可知，爆炸荷载作用下，测点1与测点2的速度时程曲线均产生了震荡，其中位于溢流道测点1的速度幅值迅速增大随后快速衰减，而位于坝顶导流墙的测点2的速度幅值快速增加后在高位持续波动，满库的速度峰值远大于空库时的速度峰值。由图3（c）可知，爆炸后测点1和测点2的加速度幅值均有大幅度的波动，满库时的加速度波动幅度明显大于空库时的加速度波动幅度。由于水的声阻抗大于空气的声阻抗，水下爆炸后产生的能量在水中耗散的速度比空气中慢，有更多的爆炸能量传入库水和坝体中。在爆轰冲击与库水的动水压力的作用下，满库水下爆炸时的动力响应比空库爆炸时的动力响应剧烈得多。

图3 爆炸时程对比分析Fig．3 Contrastive analysis of time－histories subjected to explosion

图4给出了在炸点2位置爆炸时满库与空库条件下溢流坝损伤分布的比较。由图4（a）可知，空库爆炸时，在0～4ms内对溢流坝坝体的损伤范围逐渐扩大，4ms以后随着爆炸能量在空气中快速消散，损伤范围保持稳定，损伤主要集中在炸点附近。由图4（b）可知，满库条件下水下爆炸时，溢流坝产生了较大的损伤：0～20ms内爆炸冲击波在坝体内传播并在自由面反射产生较大强度的稀疏波，该稀疏波与入射波叠加使大坝内压力降低，造成溢流坝的溢流道入口有严重的拉伸破坏；由于动水压力的影响，20ms后损伤范围沿着溢流道逐渐扩大，并且在坝体下部折坡处产生了严重的拉弯破坏。综上所述，满库时水下爆炸产生的冲击波对溢流坝坝体的损伤远大于空库时爆炸对坝体的损伤。

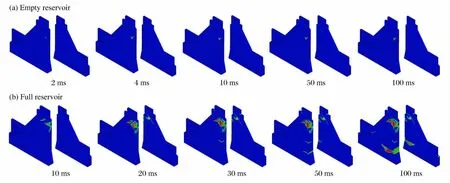
图4 损伤过程对比分析Fig．4 Contrastive analysis of the damage propagation process

5 满库时不同炸点水下爆炸溢流坝的抗爆性能

溢流坝作为大坝一个重要的部分，坝顶处有很多机电设备与闸门，因此溢流坝的动力响应对坝体上的设备有很大的影响。通过对比分析满库与空库条件下在炸点2处爆炸时溢流坝的动力响应及损伤分布可知，满库条件下溢流坝的动力响应及损伤范围更大，因此本节主要探讨满库条件下不同炸点深度爆炸时溢流坝的动力响应及损伤范围。

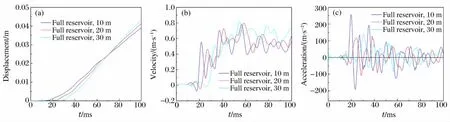
图5测点2时程对比分析Fig．5 Contrastive analysis of time－histories of gauge point 2

图5 给出了满库条件下溢流坝上游侧不同深度炸点水下接触爆炸时，测点2（坝顶导流墙）的位移、速度和加速度时程曲线。由图5（a）可知：不同炸点深度时，测点2的位移均随着时间的增加而不断增加，炸点位置越深，位移增速越快；在0～70ms时间内，炸点深度较小的位移幅值较大；70ms以后，炸点位置越深，位移幅值越大，并有进一步扩大的趋势。由图5（b）可知：不同炸点深度时，测点2的速度时程均出现了跳跃式的波动，距离测点较近的炸点首先达到峰值，在随后的波动过程中，炸点位置越深，速度幅值越大。由图5（c）可知：测点2的加速度时程在达到峰值后均出现了衰减，炸点1距离水面较近，因此在炸点1爆炸时，坝体顶部的产生加速度最大，但能量耗散较快，加速度幅值衰减较快；炸点2与炸点3在水下较深位置，爆炸后产生的初始加速度峰值较炸点1小，但加速度峰值衰减较缓慢。由于水的阻抗小于混凝土的阻抗，水下接触爆炸后，爆炸冲击波携带的能量一部分通过水体传播，一部分以压缩应力波的形式传播到坝体内。炸药位置越深，水压力对炸药的约束越强，炸药爆炸后能量耗散就越慢，同时入射进入坝体内的冲击波能量越多，从而大坝的动力响应越大。综上所述，满库条件下水下接触爆炸时，溢流坝的动力响应均较大，在0～30m的水深范围内，炸点位置越深，动水压力对坝体动力响应的影响越大。

图6给出了满库条件下在不同深度炸点位置爆炸时测点2（坝顶导流墙）的加速度反应谱。从图6可以看出：满库条件下在炸点1处爆炸时，加速度反应谱的峰值最大，约为250m／s2；在炸点2位置爆炸时，加速度反应谱峰值最小；并且加速度的峰值都集中在0～10ms的短周期范围内。靠近测点2的加速度反应谱峰值普遍较大，炸点水下位置越深，加速度反应谱峰值受动水压力的影响越大。固有周期在0～10ms范围的设备结构受到加速度波动的影响较大。

图7给出了满库条件下上游侧不同炸点深度爆炸时，溢流坝的损伤分布对比。由图7可知，3个炸点爆炸时均对坝体产生了较大的损伤。图7（a）中，炸点1爆炸对坝体的损伤主要分布在溢流坝坝体上游折坡处以及溢流道入口处，随着爆炸冲击波在坝体传播以及坝体的动力响应，在溢流道中部也产生了损伤。图7（b）为炸点2爆炸时坝体的损伤结果，随着炸点深度的下移，与炸点1相比，溢流道入口处以及溢流道的损伤程度有所减小但坝体上游折坡处的损伤程度增大许多。图7（c）是炸点3爆炸时坝体的损伤结果，在坝体上游折坡处有严重的损伤，溢流道的损伤主要集中在溢流道斜坡处及溢流道尾部。综上所述，水下爆炸均对溢流坝坝体上游折坡处产生了严重损伤，随着炸点深度的增大，溢流道的损伤分布也有下移趋势，溢流道顶部损伤减小。

图6 测点2加速度反应谱对比Fig．6 Contrastive analysis of acceleration response spectrum of gauge point 2

图7 不同炸点爆炸时坝体的损伤情况对比Fig．7 Contrastive analysis of damage propagation processes of overflow dam at different explosion points

6 结 论

以黄登重力坝为背景，建立溢流坝满库与空库爆炸的全耦合数值模型，对水下接触爆炸时溢流坝的动力响应及损伤进行了分析，所得结论如下：（1）满库条件下水下爆炸时，溢流坝的动力响应比空库时剧烈得多，损伤范围也更大。满库时溢流坝的损伤主要分布在坝顶及坝体上游折坡处，空库时损伤集中在炸点处。（2）满库条件下水下爆炸时，溢流坝的动力响应较大，炸点位置越深（0～30m水深范围内），爆炸对坝体动力响应的影响越大。溢流坝坝体上游折坡处产生了严重损伤，并且随着炸点深度的增大，溢流道损伤分布也随之下移，其顶部损伤减小。（3）炸点位置对加速度反应谱的峰值影响较大，固有周期在0～10ms范围内的设备结构受加速度波动的影响较大。

［1］ 丁阳，方磊，李忠献，等．防恐建筑结构抗爆防护分类设防标准研究［J］．建筑结构学报，2013，34（4）：57－64．Ding Yang，Fang Lei，Li Zhongxian，et al．Research on categorized explosion protection criterion of anti－terrorism building structures［J］．Journal of Building Structures，2013，34（4）：57－64．

［2］ Georgin J F，Reynouard J M．Modeling of structures subjected to impact：Concrete behaviour under high strain rate［J］．Cement and Concrete Composites，2003，25（1）：131－143．

［3］ Zhang Q，Lin D C，Bai C H，et al．Correlations of blast damage to ground surface targets with explosion seismic effect［J］．Soil Dynamics and Earthquake Engineering，2004，24（7）：519－525．

［4］ Zhao C F，Chen J Y．Damage mechanism and mode of square reinforced concrete slab subjected to blast loading［J］．Theoretical and Applied Fracture Mechanics，2013，63／64（1）：54－62．

［5］ Zhao C F，Chen J Y，Wang Y，et al．Damage mechanism and response of reinforced concrete containment structure under internal blast loading［J］．Theoretical and Applied Fracture Mechanics，2012，61（1）：12－20．

［6］ 李鸿波，张爱华，陈云敏．爆炸冲击荷载作用下重力坝三维各向异性脆性动力损伤有限元分析［J］．岩石力学与工程学报，2006，25（8）：1598－1605．Li Hongbo，Zhang Aihua，Chen Yunmin．3dfinite element analysis of anisotropic brittle dynamic damage in gravity dam under blast－impact load［J］．Chinese Journal of Rock Mechanics and Engineering，2006，25（8）：1598－1605．

［7］ 薛新华，李鹏．爆炸荷载作用下拱坝动力响应分析［J］．水利学报，2015，46（增刊1）：107－110．Xue Xinhua，Li Peng．Dynamic response analysis of arch dam under blast load［J］．Journal of Hydraulic Engineering，2015，46（Suppl 1）；107－110．

［8］ 徐俊祥，刘西拉．水中爆炸冲击下混凝土坝动力响应的全耦合分析［J］．上海交通大学学报，2008，42（6）：1001－1004．Xu Junxiang，Liu Xila．Full coupled simulation of concrete dams subjected to underwater explosion［J］．Journal of Shanghai Jiaotong University，2008，42（6）：1001－1004．

［9］ Yu T T．Dynamical response simulation of concrete dam subjected to underwater contact explosion load［C］∥2009 WRI World Congress on Computer Science and Information Engineering．Los Angeles，California，2009：769－774．

［10］ 张社荣，王高辉．混凝土重力坝抗爆性能及抗爆措施研究［J］．水利学报，2012，43（10）：1202－1213．Zhang Sherong，Wang Gaohui．Study on the antiknock performance and measures of concrete gravity dam［J］．Journal of Hydraulic Engineering，2012，43（10）：1202－1213．

［11］ 张社荣，王高辉．浅水爆炸冲击荷载下高拱坝抗爆性能分析［J］．天津大学学报，2013，46（4）：315－321．Zhang Sherong，Wang Gaohui．Antiknock performance of high arch dam subjected to shallow water explosion［J］．Journal of Tianjin University，2013，46（4）：315－321．

［12］ Zhang S R，Wang G H，Yu X R．Seismic cracking analysis of concrete gravity dams with initial cracks using the extended finite element method［J］．Engineering Structures，2013，56（6）：528－543．

［13］ 张社荣，孔源，王高辉，等．混凝土重力坝水下接触爆炸下的毁伤特性分析［J］．水利学报，2014，45（9）：1057－1065．Zhang Shenrong，Kong Yuan，Wang Gaohui，et al．Damage characteristic analysis of concrete gravity dams subjected to underwater contact explosion［J］．Journal of Hydraulic Engineering，2014，45（9）：1057－1065．

［14］ 李本平．制导炸弹连续打击下混凝土重力坝的破坏效应［J］．爆炸与冲击，2010，30（2）：220－224．Li Benping．Damage effect of a concrete gravity dam under continuous attacks of guided bombs［J］．Explosion and Shock Waves，2010，30（2）：220－224．

［15］ 张社荣，杨明，王高辉．水下爆炸冲击下重力拱坝的破坏特性［J］．水电能源科学，2014，32（7）：69－73．Zhang Sherong，Yang ming，Wang Gaohui．Failure characteristics of gravity arch dam subjected to underwater explosion［J］．Water Resources and Power，2014，32（7）：69－73．

［16］ 陆路，李昕，周晶．水下核爆作用下混凝土重力坝模型破坏试验［J］．大连理工大学学报，2011，51（6）：854－860．Lu Lu，Li Xin，Zhou Jing．Destructive tests of concrete gravity dam underwater nuclear explosion［J］．Journal of Dalian University of Technology，2011，51（6）：854－860．

［17］ Malvar L J，Ross C A．A review of strain rate effects for concrete in tension［J］．ACI Materials Journal，1998，95（6）：735－739．

［18］ Bischoff P H，Perry S H．Compressive behaviour of concrete at high strain rates［J］．Materials and Structures，1991，24（6）：425－450．

［19］ Wang W，Zhang D，Lu F，et al．Experimental study on scaling the explosion resistance of a one－way square reinforced concrete slab under a close－in blast loading［J］．International Journal of Impact Engineering，2012，49（2）：158－164．

［20］ 匡志平，袁训康．RHT混凝土本构模型强度参数分析与模拟［J］．力学季刊，2012，33（1）：158－163．Kuang Zhiping，Yuan Xunkang．The analysis and simulation for the strength parameters［J］．Chinese Quarterly of Mechanics，2012，33（1）：158－163．

［21］ Tu Z G，Lu Y．Evaluation of typical concrete material models used in hydrocodes for high dynamic response simulations［J］．International Journal of Impact Engineering，2009，36（1）：132－146．

［22］ Shin Y S，Chisum J E．Modeling and simulation of underwater shock problems using a coupled Lagrangian－Eulerian analysis approach［J］．Shock and Vibration，1997，4（1）：1－10．

［23］ Mair H U．Hydrocodes for structural response to underwater explosions［J］．Shock and Vibration，1999，6（2）：81．

［24］ Van der Veen W A．Simulation of a compartmented airbag deployment using an explicit，coupled Euler／Lagrange method with adaptive Euler domains［A］．NAFEMS，Florida，2003．

［25］ Mair H U．Hydrocode methodologies for underwater explosion structure／medium interaction［C］∥Proceeding of the 66th Shock and Vibration Symposium．Virginia，1995，2：227－248．

Antiknock performance of an overflow dam subjected to contact explosion

Xu Qiang1，2，Cao Yang1，2，Chen Jianyun1，2

（1．State Key Laboratory of Coastal and Offshore Engineering，Dalian University of Technology，Dalian 116024，Liaoning，China；2．Institute of Earthquake Engineering，Faculty of Infrastructure Engineering，Dalian University of Technology，Dalian 116024，Liaoning，China）

In this paper，against the background of the Huangdeng gravity dam and in consideration of the influence of the concretes high strain rate，we established a fully－coupled numerical model for the dam－water－air－explosive using the Lagrange－Euler coupling method，and studied the antiknock performance of the overflow dam subjected to contact explosion loading．The dynamic response and damage of the overflow dam under the condition of withholding a full reservoir of water were compared with that under the condition of withholding an empty reservoir．Further，the response of the overflow dam subjected to underwater explosion at different explosion points was also investigated．The results show that，subjected to the same underwater explosion，the dynamic response and damage degree of the overflow dam withholding a full reservoir were significantly higher than those of the dam withholding an empty reservoir，and the weak points of the overflow dam were mainly located at the dams overflow spillway on the top and the upstream slope．Therefore，it is concluded that research on the antiknock performance of an overflow dam subjected to underwater contact explosion should focus on the damage characteristics of the dam withholding a full reservoir．

overflow dam；contact explosion；dynamic response；damage；antiknock performance

O383．1国标学科代码：1303520

A

10．11883／1001－1455（2017）04－0677－08

（责任编辑 王玉锋）

2015－12－25；

2016－04－11

国家重点基础研究发展计划“973”项目（2013CB035905）；国家重点研发计划项目（2017YFC0404900）；国家自然科学基金重点项目（51138001，51178081）；辽宁省教育厅重点实验室项目（LZ2015022）；中央高校基本科研业务费专项资金项目（DUT15LK34，DUT14QY10）

徐 强（1982－ ），男，博士，副教授；通信作者：陈健云，chenjydg＠dlut．edu．cn。