非负稀疏表示的多标签特征选择*
2017-07-31蔡志铃
蔡志铃,祝 峰
闽南师范大学 粒计算重点实验室,福建 漳州 363000
非负稀疏表示的多标签特征选择*
蔡志铃,祝 峰+
闽南师范大学 粒计算重点实验室,福建 漳州 363000
+Corresponding author:E-mail:w illiam fengzhu@gmail.com
CAIZhiling,ZHUW illiam.M ulti-label feature selection via non-negative sparse representation.Journal of FrontiersCom puter Scienceand Technology,2017,11(7):1175-1182.
在多标签学习中,数据降维是一项重要而又具有挑战性的任务。特征选择是一种高效的数据降维技术,它通过保持最大相关信息选取一个特征子集。通过对子空间学习的研究,提出了基于非负稀疏表示的多标签特征选择方法。该方法可以看成是矩阵分解问题,其融合了非负约束问题和L2,1-范数最小优化问题。设计了一种高效的矩阵更新迭代算法求解新问题,并证明其收敛性。最后,对6个实际的数据集进行了测试,实验结果证明了算法的有效性。
1 引言
高维数据中存在着许多冗余或不相关的特征,从而面临着维数灾难问题。一方面需要较高的计算时间和空间;另一方面容易给分类带来不利之处,例如过拟合。因此数据降维是机器学习中一项重要而又具有挑战性的任务。数据降维主要分为特征提取和特征选择,前者是把原始特征近似投影到一个较低维的特征空间[1],后者是通过某种规则选取一个比较小的特征子集[2]。与特征提取不同,特征选择可以保留原始特征的物理意义,因此受到许多学者的广泛关注。考虑其是否依赖分类算法,特征选择一般分为包类算法[3]和过滤式算法[4]。包类算法把分类算法嵌入到特征选择中,虽然可以提高分类精度,但需要更高的计算时间。过滤式算法独立于分类算法,可以看作对数据的预处理。此外,对于是否考虑标签信息,特征选择可以简单地分为有监督和无监督。无监督的特征选择算法是在标签缺失的情况下利用数据特征本身建立特征选择规则[5]。有监督的特征选择算法则是利用标签信息评价特征的重要度,例如 fisher score[6]、(m inimal-redundancy-maximalrelevance criterion,mRMR)[7]等。
多标签学习是处理每个样本同时属于多个标签的数据[8]。与传统的单标签学习一样,多标签学习同样面临着维数灾难问题,而且更复杂。因此,为了提高学习算法的效果,许多学者致力于研究多标签数据特征选择方法,去除不相关或冗余特征。许多研究者首先将多标签数据转换成单标签数据,然后使用现有的单标签特征选择算法进行处理[9-10]。常用的数据转换方法有二元关系法(binary relevance,BR)[11]、标签幂集法(labelpowerset,LP)[12]等。近几年有些学者提出了利用特征与标签之间的多元互信息评价特征重要度,然后用特征排序算法或贪婪算法进行特征选择,如PMU(multivariatemutual information for multi-label feature selection)[13]、FIMF(fastmulti-label feature selection based on information-theoretic feature ranking)[14]和 MDMR(multi-label feature selection based onmax-dependency andmin-redundancy)[15]等。
本文融合求解非负约束问题和L2,1-范数最小优化问题,提出了一种新的基于非负稀疏表示的多标签特征选择方法。首先,利用特征子空间和标签空间的线性关系构造误差项,并对系数矩阵加以非负约束;其次,引入指示矩阵刻画特征子空间,放松指示矩阵为非负约束并加入稀疏表示项L2,1-范数,将离散问题转换为连续问题,定义特征重要度的评价准则;再次,设计一种高效的矩阵更新迭代算法求解该问题,并证明了其收敛性;最后,实验结果表明本文算法对多标签数据具有很好的特征选择性能。
本文组织结构如下:第2章介绍一些相关工作;第3章提出新的多标签特征选择算法;第4章进行实验结果分析;第5章进行总结和展望。
2 相关工作
一般的多标签问题会给学习任务带来很大的困难,主要采用3种不同的设计策略:一阶策略、二阶策略和高阶策略。其中一阶策略是一种直接的策略,将多标签学习分解成一些二类单标签问题。对每个标签单独考虑,而不考虑标签之间的相关性。在每个标签的二分类问题中,样本如果含有此标签,则称为正样本,反之为负样本。然而,这种策略会导致数据分布不平衡和样本的稀疏性。为了克服类别分布不平衡,Zhang等人提出了一种适用于多标签数据的K近邻多标签学习算法(multi-label K-nearestneighbor,ML-K NN)[16]。它同样是把多标签分类问题分解成多个二类分类问题。首先,利用训练集的每个样本分别找对应的k个邻居,计算先验概率和后验概率。然后,对每个未知的样本找到它的k个邻居,利用贝叶斯公式,通过已求得的先验概率和后验概率判定未知样本是否含有此标签。
子空间学习是较为流行的一种特征降维方法之一,被广泛应用于机器学习等领域。子空间学习把原始高维数据转换到一个低维的子空间,在低维空间保持原始数据的结构或特性进行学习。子空间学习常常被用于特征提取中,如主成分分析(principal component analysis,PCA)[17]、线性判别分析(linear discriminantanalysis,LDA)[18]等。近年来也有学者将子空间学习用于特征选择中[19],取得了很好的效果。
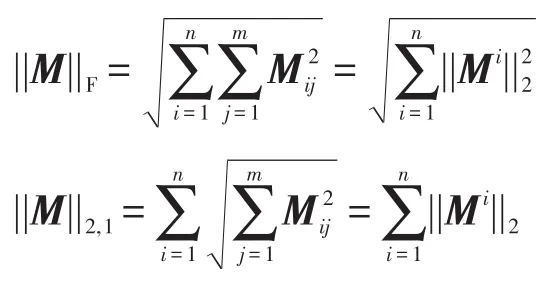
3 非负稀疏表示的特征选择
本文引入子空间学习,提出了基于非负稀疏表示的多标签特征选择方法。融合求解非负约束问题和L2,1-范数最小优化问题,设计了一种高效的矩阵更新迭代算法,并证明其收敛性。
3.1 问题描述
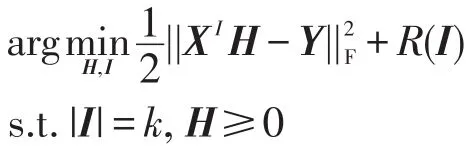
为了表示 XI,引入指示矩阵来代替所选择特征的指标集。不失一般性,可以定义指示矩阵W如下:

这里指示矩阵W的行数等于所有原始特征的个数,其列数等于被选择出来的特征个数。例如d=5,I={1,3,5},则:
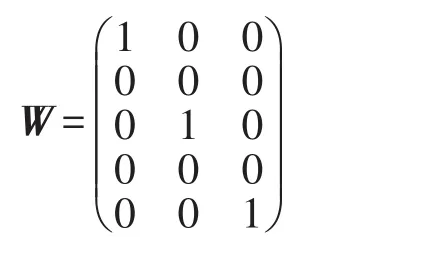
基于指示矩阵W,目标函数可化为:
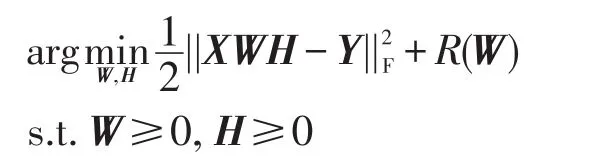
原始问题是离散问题,这里放松了条件,将原来的离散问题转化成连续问题来求解。记W=(w1,,则||wi||2可以作为第i个特征的权重。为此,设置正则项R(W)为L2,1-norm范数||W||2,1。最后目标函数如下:
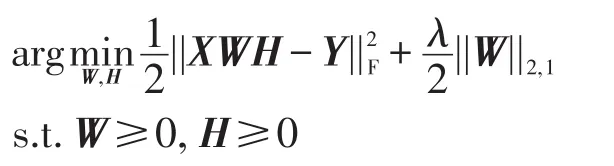
其中,λ作为参数调节误差项和正则项之间的比重;||W||2,1限定矩阵W的行稀疏。
3.2 问题优化
根据文献[20],L2,1-norm最小优化问题可以通过迭代问题求解如下:
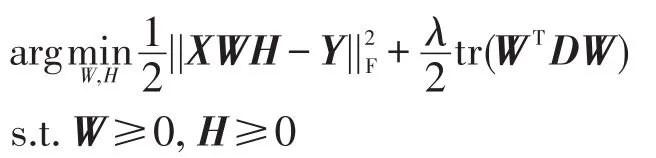
为求解非负约束问题,构造拉格朗日函数如下:
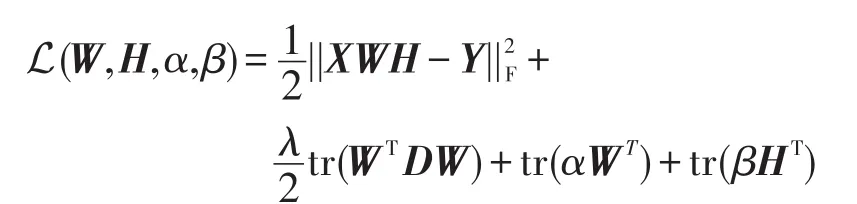
其中,α、β是拉格朗日乘子,目的是保证W、H非负。令L对W和H的导数为0:
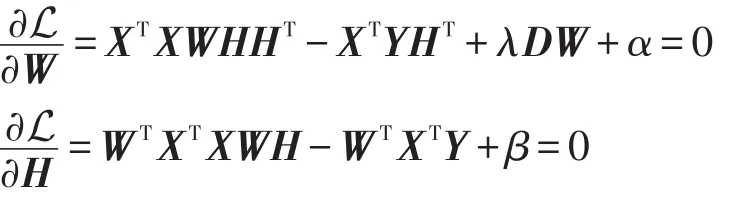
根据Kuhn-Tucker条件,对于任意的i、j,有αijWij=0和βijHij=0。由此,可以得到更新规则:
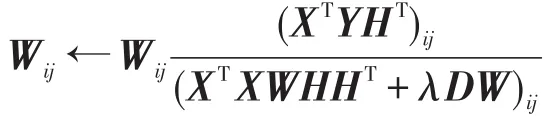
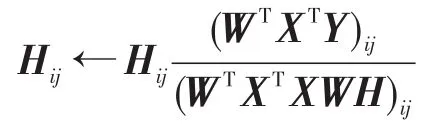
3.3 算法与时间复杂度分析
根据以上优化分析,非负稀疏表示的多标签特征选择(multi-label feature selection based non-negative sparse representation,MNMFS)算法如下。
算法1MNMFS算法
输入:数据矩阵 X∈ℝn×d,标签矩阵Y∈ℝn×m,特征选择个数k,参数λ。
输出:选择的特征指标集I,其中|I|=k。
1.初始化W和H;
2.迭代
2.2固定D和H,更新W,其中
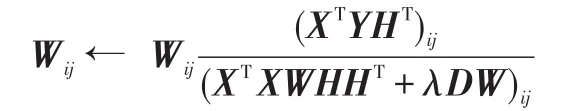
2.3固定D和W,更新H,其中
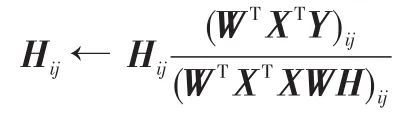
3.直到收敛;
4.记W=(w1,w2…,wd)T,降序排列||wi||2,i=1,2,…,d ,选择前k个为特征指标集I。
通常情况下,m<n,m<d,k<n和k<d。根据算法得出,在每一步迭代中,更新D的复杂度是O(dk),更新W的复杂度是O(d2n),更新H的复杂度是O(kdn)。因此总的时间复杂度是O(td2n),其中t是迭代次数。因为t值较小,所以时间依赖于数据的特征维数d和数据的样本个数n。
3.4 收敛性分析
首先,介绍几个定义和重要引理。
定义1(辅助函数)[21]函数 Z(v,v′)称为函数F(v)的辅助函数,如果它满足如下条件,对于任意的v和v′,有:
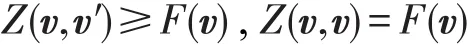
引理1[21]如果Z(v,v′)是F(v)的一个辅助函数,那么F(v)在如下更新下单调递减:
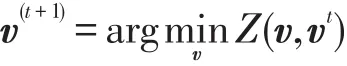
引理2[22]对于任意矩阵,且 A 、B 是对称矩阵,那么下面的不等式成立:
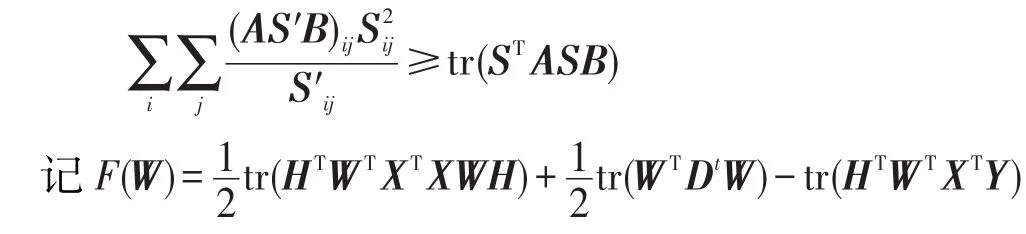
那么函数
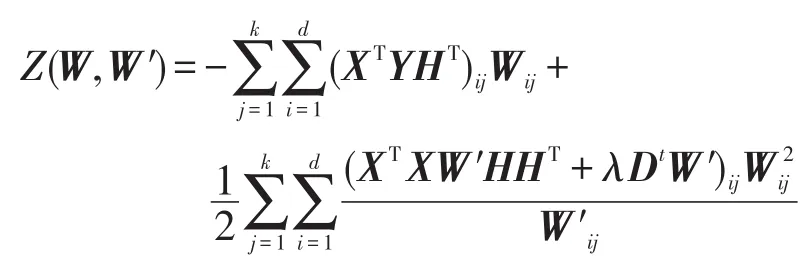
是F(W)的辅助函数,并且Z(W,W′)对于W 是凸函数,其全局最优解为:
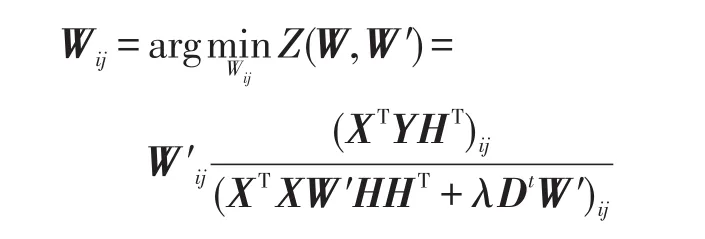
证明首先证明Z(W,W′)是F(W)的辅助函数。
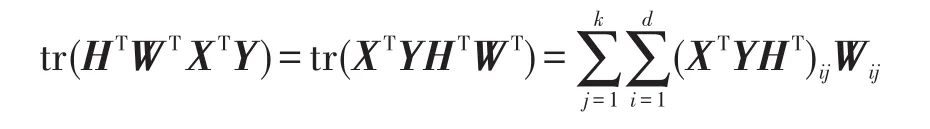
利用引理2,有:
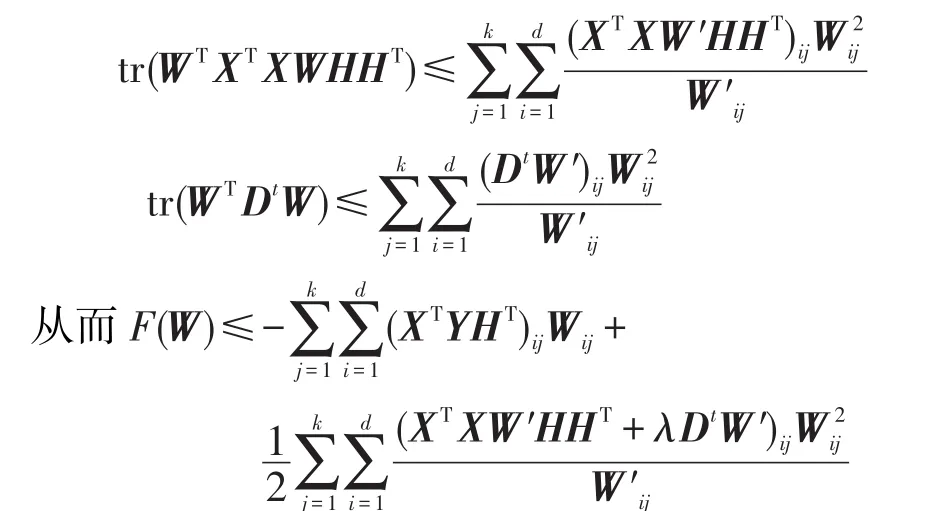
这就证明了对任意的W 、W′,都有F(W)≤Z(W,W′)。
另外,显然有Z(W,W)=F(W)。
因此证明了Z(W,W′)是F(W)的一个辅助函数。
为了得到Z(W,W′)的最小值,计算Z(W,W′)对Wij的一阶偏导数:
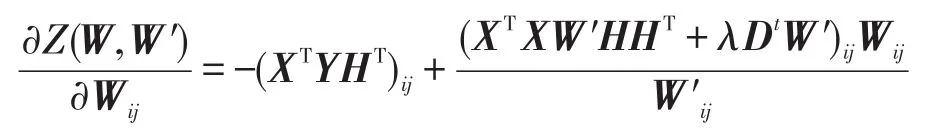
同时,Z(W,W′)的二阶偏导数,即它的Hassian矩阵为:
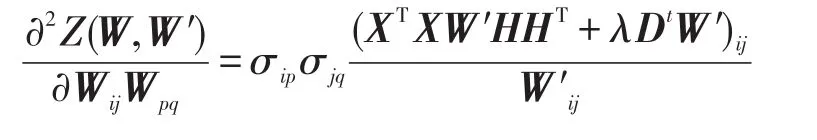
其中,当x=y时,σxy=1;否则σxy=0。显然Hassian矩阵的所有值非负,因此辅助函数Z(W,W′)是一个凸函数,并在时对应的W为它的全局最优值。
根据引理1可以得到:

4 实验
对本文算法和现有的几种多标签特征选择算法在6个公开的现实数据集上做了大量的实验。实验结果表明,本文算法在多标签数据集上有较好的特征选择性能。
4.1 实验数据
用6个来自3种不同应用领域的真实数据集验证本文多标签特征选择算法。这6个数据集分别是Society、Health、Arts、Recreation、Scene和 Yeast。其中Society、Health、Arts和Recreation数据集属于网页类数据集,Scene数据集属于图像类数据集,Yeast数据集属于基因类数据集。数据集从Mulanlibrary(http://mulan.sourceforge.net/datasets-m lc.htm l)下载获得,在表1中列出这些数据集的详细信息。
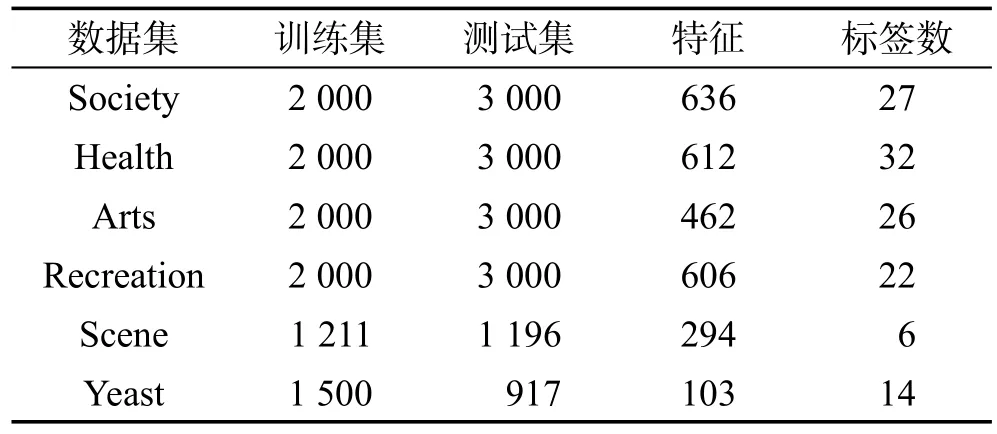
Table 1 Data information表1 数据信息
4.2 实验设置
实验用ML-KNN作为评价分类算法,其中邻域个数K=10,平滑指数s=1。选择现有的多标签特征选择算法(PMU,MDMR,FIMF)作为对比算法,分别考虑它们的5个评价指标Average precision、Coverage、Hamm ing loss、One-error和 Ranking loss。对比算法的实验设置均按照默认设置,除了FIMF在数据集Scene上设置Q=6,是因为数据集Scene只有6个标签。对于本文算法,设置参数λ=1,迭代次数为50。由于算法对矩阵初始化有一定敏感性,采用10次实验,取结果的平均值。另外,对数据集Society、Health、Arts、Recreation、Scene,分别在选择特征数为{30:5:70}时对所有算法进行实验。对数据集Yeast,因为特征数较少,所以设定选择的特征个数为{10:5:50}。
4.3 实验结果分析
本文根据实验设置,对不同算法和数据集做了大量的实验。图1分别表示各个数据集在选择不同特征个数情况下,所有算法的平均分类精度,其中水平线表示原始的平均分类精度。从图中首先可以得出,特征选择不仅缩短了分类学习的运行时间和空间,有时候还提高了分类学习性能。这是因为特征选择删除了一些不相关或冗余的特征,解决了维数灾难,在一定程度上避免过拟合。然后还可以得出,本文算法在大多数情况下优于对比的多标签特征选择算法。
此外,为了更加细致地分析每个算法的效果,将ML-KNN作为分类算法,表2~表6分别列出来了所有算法在所有数据集上对不同评价指标的性能。这里每个算法对实验设置的特征选择个数都做了实验,分别取每个算法中最好的结果。表中对不同的评价指标,用符号↑表示该指标值越大,性能越优;用符号↓表示该指标值越小,性能越优;用黑体标注对比算法中最优性能的结果。从表中可以得出,在90种对比情况下,本文算法仅有8种情况性能略低于不同的对比算法。在Scene数据集中,本文算法在Average precision、Hamm ing loss、One-error评价指标中性能较低于PMU算法。但从其他数据集上看,本文算法性能较优于PMU算法。总体上,本文多标签特征选择算法在以上数据集有比较好的适用性,性能要优于对比的多标签特征选择算法。
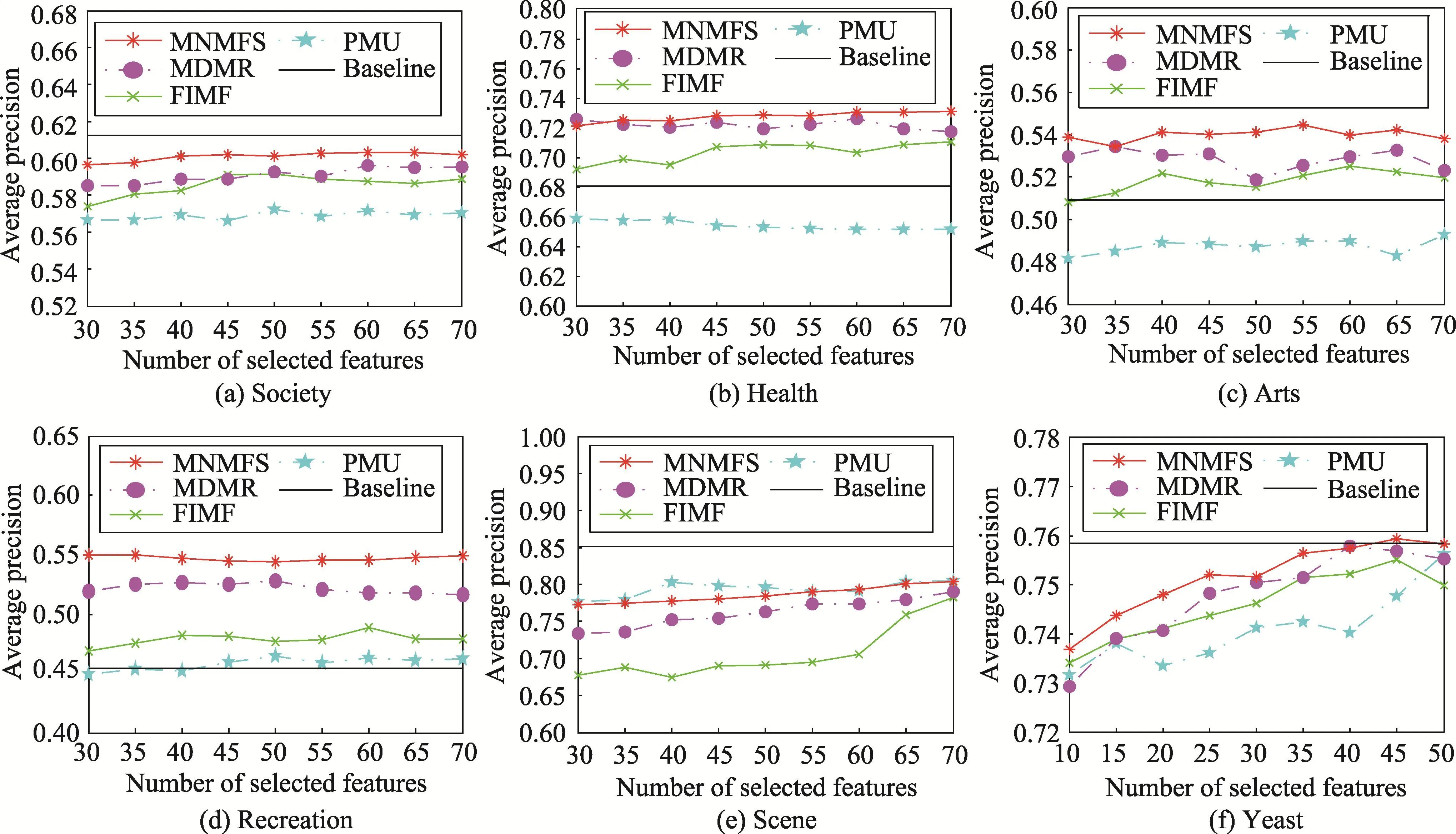
Fig.1 Comparison on average precision of differentalgorithms图1 不同算法的平均分类精度比较
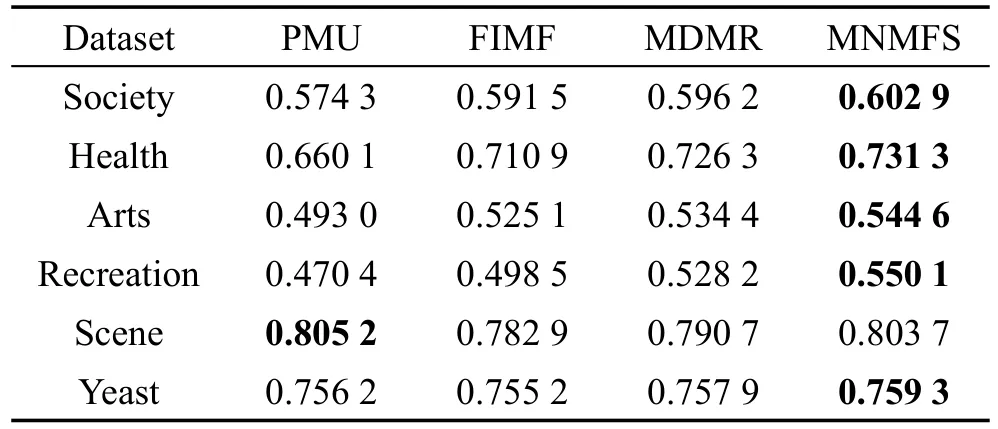
Table2 Performanceof average precision表2 平均精度↑
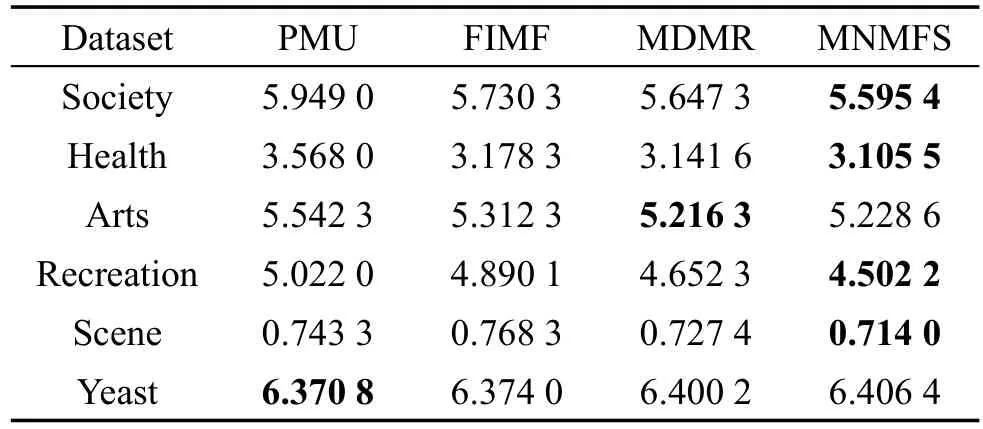
Table3 Performanceof coverage表3 覆盖率↓
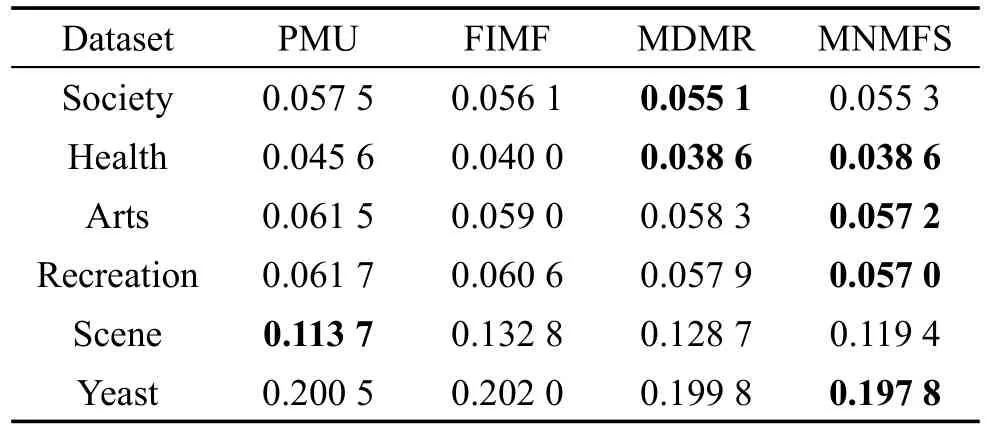
Table4 Performanceof Hamm ing loss表4 汉明损失↓
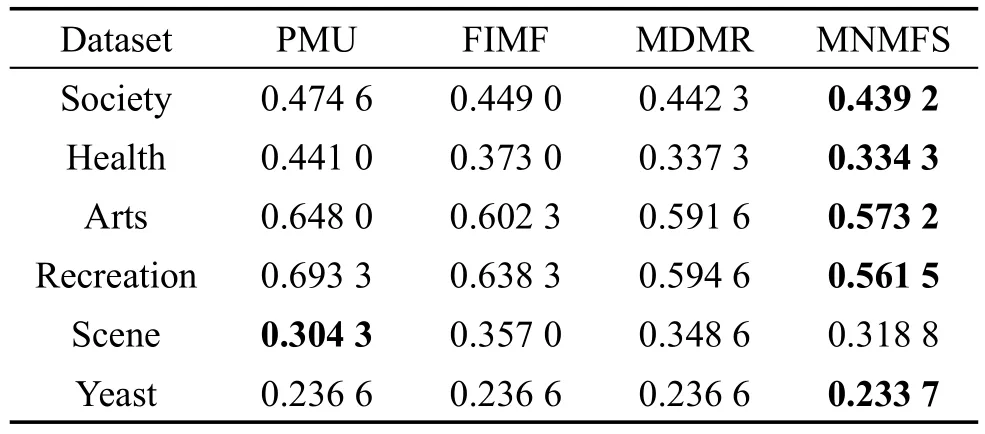
Table5 PerformanceofOne-error表5 One-错误率↓
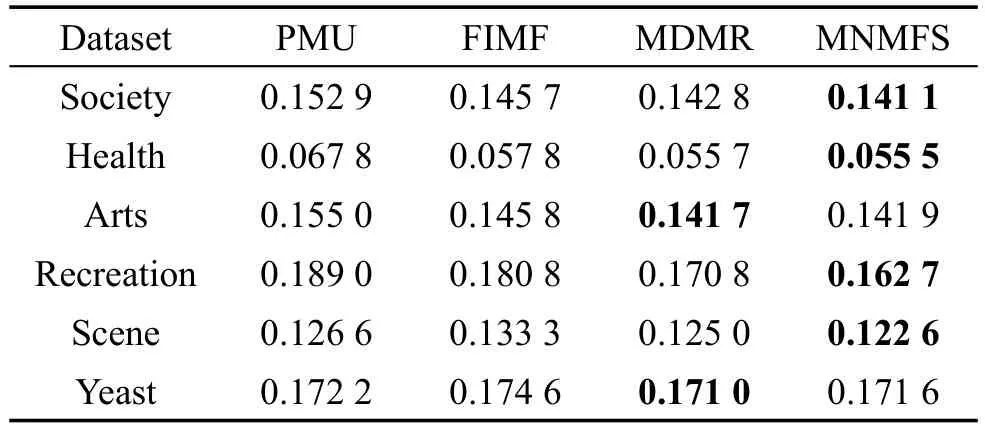
Table 6 Performance of Ranking loss表6 排序损失↓
5 结束语
多标签学习是处理一个样本同时含有多个标签的数据。同传统的单标签学习一样,也面临着维数灾难。本文提出了一种基于非负稀疏表示的多标签特征选择算法。通过引入子空间学习,对特征子空间加以非负和稀疏表示。融合非负约束问题和L2,1-范数最小优化问题,设计了一种新的矩阵更新迭代算法求解该问题。最后,为了验证算法的有效性,在3种不同领域的真实数据集上做了大量的实验。实验结果表明,本文多标签特征选择算法优于现有的几种多标签特征选择算法。
算法的原始问题是离散问题,本文在转化成连续问题求解时,只考虑指示矩阵的非负约束和行稀疏性,而没有考虑其存在的正交性。在以后的研究工作中将考虑正交约束,提高算法的性能,并把非负稀疏分析用于其他弱监督学习和无监督学习中,以解决更多问题。
[1]Zhang Yin,Zhou Zhihua.Multilabel dimensionality reduction via dependence maxim ization[J].ACM Transactions on Know ledge Discovery from Data,2010,4(3):14.
[2]CaiDeng,Zhang Chiyuan,He Xiaofei.Unsupervised feature selection formulti-cluster data[C]//Proceedings of the 16th ACM SIGKDD International Conference on Know ledge Discovery and Data M ining,Washington,Jul 25-28,2010.New York:ACM,2010:333-342.
[3]Maldonado S,Weber R.A w rappermethod for feature selection using support vectormachines[J].Information Sciences,2009,179(13):2208-2217.
[4]Yu Lei,Liu Huan.Feature selection for high-dimensional data:a fast correlation-based filter solution[C]//Proceedings of the 20th International Conference on Machine Learning,Washington,Aug 21-24,2003.Menlo Park,USA:AAAI,2003:856-863.
[5]Wang Shiping,Pedrycz W,Zhu Qingxin,et al.Unsupervised feature selection via maximum projection and m inimum redundancy[J].Know ledge-Based Systems,2015,75:19-29.
[6]Duda R O,Hart PE,Stork D G.Pattern classification[M].New York:JohnWiley&Sons,Inc,2012.
[7]Peng Hanchuan,Long Fuhui,Ding C.Feature selection based on mutual information criteria ofmax-dependency,maxrelevance,and m in-redundancy[J].IEEE Transactions on Pattern Analysis and Machine Intelligence,2005,27(8):1226-1238.
[8]Zhang M inling,Zhou Zhihua.A review onmulti-label learningalgorithms[J].IEEE Transactions on Know ledge and Data Engineering,2014,26(8):1819-1837.
[9]Yang Yiming,Pedersen JO.A comparative study on feature selection in text categorization[C]//Proceedings of the 14th International Conference on Machine Learning,Nashville,USA,Jul 8-12,1997.Menlo Park,USA:AAAI,1997,97:412-420.
[10]Diplaris S,TsoumakasG,M itkas PA,etal.Protein classification w ith multiple algorithms[C]//LNCS 3746:Proceedings of the 10th Panhellenic Conference on Advances in Informatics,Volos,Greece,Nov 11-13,2005.Berlin,Heidelberg:Springer,2005:448-456.
[11]BoutellM R,Luo Jiebo,Shen Xipeng,etal.Learningmultilabel scene classification[J].Pattern Recognition,2004,37(9):1757-1771.
[12]Read J,Pfahringer B,Holmes G.Multi-label classification using ensembles of pruned sets[C]//Proceedings of the 8th International Conference on Data M ining,Pisa,Italy,Dec 15-19,2008.Washington:IEEE Computer Society,2008:995-1000.
[13]Lee J,Kim DW.Feature selection formulti-label classification usingmulti-variatemutual information[J].Pattern Recognition Letters,2013,34(3):349-357.
[14]Lee J,Kim DW.Fastmulti-label feature selection based on information-theoretic feature ranking[J].Pattern Recognition,2015,48(9):2761-2771.
[15]Lin Yaojin,Hu Qinghua,Liu Jinghua,etal.Multi-label feature selection based onmax-dependency andm in-redundancy[J].Neurocomputing,2015,168:92-103.
[16]Zhang M inling,Zhou Zhihua.ML-K NN:a lazy learning approach to multi-label learning[J].Pattern Recognition,2007,40(7):2038-2048.
[17]Jolliffe I.Principal component analysis[M].Secaucus,USA:Springer-Verlag,2002.
[18]Fisher R A.The use ofmultiplemeasurements in taxonomic problems[J].Annalsof Eugenics,1936,7(2):179-188.
[19]Wang Shiping,Pedrycz W,Zhu Qingxin,et al.Subspace learning for unsupervised feature selection viamatrix factorization[J].Pattern Recognition,2014,48(1):10-19.
[20]Nie Feiping,Huang Heng,CaiXiao,etal.Efficientand robust feature selection via joint L2,1-norms m inim ization[C]//Advances in Neural Information Processing Systems 23:Proceeding of the 24th Annual Conference on Neural Information Processing Systems,Vancouver,Canada,Dec 6-9,2010.Red Hook,USA:Curran Associates,2010:1813-1821.
[21]Lee D D,Seung H.Algorithms for non-negativematrix factorization[C]//Advances in Neural Information Processing Systems 14:Proceeding of the 15th Conference on Neural Information Processing Systems,Vancouver,Canada,Dec 3-8,2001.Cambridge,USA:M ITPress,2001:556-562.
[22]Ding C,Li Tao,Jordan M I.Convex and sem i-nonnegative matrix factorizations[J].IEEETransactions on Pattern Analysisand Machine Intelligence,2010,32(1):45-55.

CAIZhiling was born in 1989.He is an M.S.candidate at M innan Normal University.His research interests includemachine learning and datam ining.
蔡志铃(1989—),男,福建漳州人,闽南师范大学硕士研究生,主要研究领域为机器学习,数据挖掘。

祝峰(1962—),男,江西玉山人,2006年于奥克兰大学计算机科学专业获得博士学位,现为闽南师范大学教授,主要研究领域为数据挖掘,人工智能。
M ulti-Label Feature Selection via Non-Negative Sparse Representation*
CAIZhiling,ZHUWilliam+
Lab of Granular Computing,M innan NormalUniversity,Zhangzhou,Fujian 363000,China
Dimensionality reduction isan importantand challenging task inmulti-label learning.Feature selection is a highly efficient technique for dimensionality reduction bymaintainingmaximum relevant information to find an optimal feature subset.Firstof all,this paper proposes amulti-label feature selectionmethod based on non-negative sparse representation by studying the subspace learning.Thismethod can be treated as amatrix factorization problem,which is combined w ith non-negative constraintproblem and L2,1-norm minimization problem.Then,thispaper designs a kind of efficient iterative update algorithm to tackle the new problem and proves its convergence.Finally,theexperimental resultson six real-world data setsshow theeffectivenessof the proposed algorithm.
multi-label learning;feature selection;non-negativematrix factorization;L2,1-norm
m wasborn in 1962.He
the Ph.D.degree in computer science from University of Auckland in 2006.Now he is a professor atM innan Normal University.His research interests include datam ining and artificial intelligence.
A
:TP18
*The NationalNatural Science Foundation of ChinaunderGrantNos.61379049,61379089(国家自然科学基金面上项目).Received 2016-05,Accepted 2016-07.
CNKI网络优先出版:2016-07-14,http://www.cnki.net/kcms/detail/11.5602.TP.20160714.1616.010.htm l
关键词:多标签学习;特征选择;非负矩阵分解;L2,1-范数
