一种雷达卫星标校中的野值剔除方法

王建富，吴金海，钮俊清，郭佳意

(1.中国电子科技集团公司第三十八研究所孔径阵列与空间探测安徽省重点实验室，安徽 合肥230088； 2.太原卫星发射中心，山西 太原 030027)



一种雷达卫星标校中的野值剔除方法

王建富1，吴金海2，钮俊清1，郭佳意1

(1.中国电子科技集团公司第三十八研究所孔径阵列与空间探测安徽省重点实验室，安徽 合肥230088； 2.太原卫星发射中心，山西 太原 030027)

通过卫星标校方式提高雷达系统测量精度时，雷达获取的测量点迹对标定结果的影响巨大，尤其存在野值点的情况下，雷达系统误差标定可能失效。提出了基于雷达卫星标校的野值剔除方法，首先将测量值与真实星历值对比，得到雷达的初始系统误差和随机误差，并以此确定测量点迹的波动范围，排除部分野值；然后利用剔除野值后的数据，以同样的方式确定波动范围，对测量点迹重新进行野值剔除；最后利用过滤后的测量点迹进行雷达系统误差的标定。实验结果表明，该方法得到的雷达系统误差和随机误差变小，能够提高雷达系统测量精度。

卫星标校；野值剔除；系统误差

0 引 言

系统标定是确保雷达系统测量精度最关键的环节，其中通过卫星对雷达系统进行标定是目前一种常规且先进的方法。该方法通过比对近地轨道卫星的测量数据与精密星历(即精轨数据)，分析解算出各项误差系数，既能克服天气等因素的影响，又适应了雷达的动态技术状态[1]。

但是在实际的观测任务中，雷达接收的信号，由于杂波、噪声或人为干扰，可能存在或多或少的点迹，在距离、方位或仰角上与观测目标的实际运行轨迹相去甚远，此类点我们称为野值点。尽管现代雷达采用了诸多信号处理技术，但是总会遗漏一小部分杂波或干扰信号，从而构成野值点，在卫星标校计算时，这些野值点可能造成系统误差系数无法反映雷达真实的测量精度，进而导致系统误差标定失效。本文针对如何剔除野值、提高雷达系统测量精度的问题展开研究。

1 野值介绍

在各种数据处理问题中，由于传感器本身或者数据传输中的种种原因，都可能造成测量序列中包含某些错误的测量值，工程上称为野值[2]。在雷达系统中，接收的回波信号，经过信号处理、恒虚警检测等一系列处理后输出的信号如果超过某个设定的检测门限，便可判断为发现目标[3]。

通过设定门限的方法排除干扰产生的信号，是一种常规方式。但是门限的设定难以把握，门限设定低会造成较多虚警，门限设定高可能将真实目标排除。虽然信号处理可以过滤绝大多数的虚假信号，但是虚警信号的遗漏无法避免，因而形成的野值点会给雷达数据处理工作带来十分不利的影响。

1.1 野值成因

野值的出现来自多方面的影响，主要因素如下[4]：

(1) 操作和记录时的过失，以及数据复制和计算处理时所出现的过失性错误，由此产生的误差称为过失误差；

(2) 探测环境的变化，探测环境的突然改变使得部分数据与原先样本的模型不符合，例如雷达跟踪时应答机工作状态的不稳定等；

(3) 实际采样数据中也可能出现另一类异常数据，它既不是来自操作和处理的过失，也不是由突发性强影响因素导致的，而是某些服从长尾分布的随机变量作用的结果。

1.2 野值对系统标校的影响

无论对雷达系统实时的数据处理还是事后数据分析，野值的存在都会造成处理结果失真。卫星标校中的野值点会导致系统误差剧烈波动，不同的观测任务下得到的系统误差相差较大，无法反映雷达系统的正常状态和测量精度，因此对于野值的剔除是十分必要的。但是如果野值剔除算法选择不当，可能造成野值剔除不理想或者将部分非野值点错剔的情况。

2 野值剔除算法

本文提出的野值剔除算法对比测量点迹和精轨数据，通过多次筛选达到剔除野值的目的。流程如图1所示。

2.1 计算初始系统误差和随机误差

雷达初始系统误差和随机误差的计算过程如图2所示。

首先获取雷达测量数据以及对应的卫星编号的精密轨道综合预测格式(CPF)或大地坐标系(WGS)精轨数据。由于精轨数据采样周期比较长，所以需要对精轨数据进行插值：以测量点迹时间为基准，通过拉格朗日多项式对CPF或WGS精轨数据进行插值计算，得到与每个测量点迹相对应的精轨数据[5]，拉格朗日插值为：

(1)

式中：li(t)为插值基函数；n为阶数；ln(t)为内插卫星精轨的位置；t即为观测时刻；xi为精密星历给出的ti时刻的卫星三维坐标(R，A，E)。

然后对精轨数据进行坐标转换，将插值后地心直角坐标系下的精轨数据转换到雷达站心坐标系，与雷达测量数据统一。

(2)

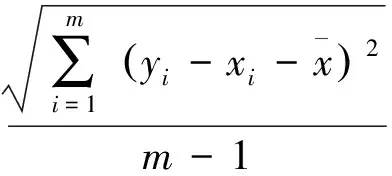
(3)

2.2 一次野值剔除

得到初始系统误差和随机误差后，进行第1次野值剔除，具体算法流程如图3所示。

根据初始系统误差和随机误差，首先通过公式(2)、(3)分别得到原始测量点迹的波动范围。其中ymin和ymax为测量点迹的距离、方位和仰角的上限与下限，系数k用于调节波动范围，一般取值3～5：

(4)

然后根据ymin和ymax依次对测量点迹进行筛选，对于不能同时满足条件(5)的点迹剔除，从而完成第1次野值剔除：

(5)

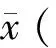
2.3 二次野值剔除及系统误差标定

同第1次野值剔除处理相同，在进行第2次野值剔除时首先通过公式(4)确定原始测量点迹的波动范围；然后根据条件(5)对所有的原始点迹进行野值判断；最后根据筛选得到的测量点迹以及对应的精轨数据通过公式(2)、(3)得到最终的雷达系统误差和随机差。具体流程如图4所示。

3 实验效果

已知某脉冲测量雷达安装调试后参数如下：

(1) 雷达参数：最大作用距离R≥ 3 000 km；测距随机误差σR=5 m；测角随机误差σθ=0.15 mrad；目标发现仰角E=5°。

(2)卫星参数：卫星NASA，编号39451、39452、39453。

在野值剔除之前得到测量点迹和精轨数据的一次差结果如图5所示，存在比较明显的野值点。通过本文的算法筛选后，各个变量下的野值都被排除，k=5。具体结果如表1所示，从实验结果可以看出，野值剔除后雷达的系统误差和随机误差显著稳定，有助于提升雷达测量精度。

表1 野值剔除前后雷达系统误差和随机差的比较

4 结束语

野值的存在对于雷达数据处理非常不利，严重影响雷达误差标定的效果。为了更加可靠地得到雷达的系统误差，本文提出一种野值剔除方法，该方法根据测量值与真实星历值，首先得到雷达的初始系统误差和随机误差，并以此完成第1次野值剔除，进而以同样的方式利用剔除野值后的测量点迹与真实星历值进行二次野值剔除，并得到最终的雷达系统误差。通过实验验证了本文算法的有效性，同时也证明了野值剔除的必要性。野值的剔除能够使标校结果更为客观、准确、可信。

[1] 郭佳意，钮俊清.雷达卫星标校的工程实现研究[J].空军预警学院学报,2014,28(3):165-167.

[2] 秦勤.雷达目标跟踪滤波算法的研究[D].大连:大连海事大学,2006.

[3] 何友.雷达数据处理及应用[M].2版.北京：电子工业出版社,2009.

[4] 胡绍林,孙国基.靶场外测数据野值点的统计诊断技术[J].宇航学报,1999,20(2)：68-74.

[5] 赵辉, 张书毕, 张秋昭,等.基于质心拉格朗日插值的GPS轨道标准化方法[J].全球定位系统，2011,36(2):15-18.

AnOutlierEliminationMethodinSatelliteCalibrationforRadar

WANG Jian-fu1,WU Jin-hai2,NIU Jun-qing1,GUO Jia-yi1
(1.Key Lab of Aperture Array and Space Application,No.38 Research Institute, China Electronics Technology Group Corporation,Hefei 230088,China; 2.Taiyuan Satellite Launch Center,Taiyuan 030027,China)

In the process of improving the measurement precision of radar system through satellite calibration mode,the original measured trace obtained from radar has a great influence on the calibration results.Especially with outliers existing,the calibration for the radar system error ceases to be effective.In this paper,an outlier elimination method based on satellite calibration for radar is proposed.Firstly,by contrasting the measured value to real value of the same satellite track,the initial radar system error and random error are achieved,which is used to get the fluctuate range of measured trace and further to remove partial outliers.Then in the same way,uses the measured trace after outlier elimination,the new fluctuate range is determined and used to eliminate outliers.At last the satellite calibration of radar system error is carried on by using the measured value after the second outlier elimination.Experimental results show that the radar system error and random error achieved by the proposed approach become small,which can improve the measurement precision of radar system.

satellite calibration;outlier elimination;system error

2017-03-06

TN957.51

：A

：CN32-1413(2017)03-0054-04

10.16426/j.cnki.jcdzdk.2017.03.013