物理模型的建构与变式探究

林智勇

【摘 要】 物理模型是物理过程或现象的直观显现，物理解题的过程，实质上是物理模型的还原过程，而变式既属于教学行为，也指一种教学策略。在物理问题的解决过程中，经常需要建立物理模型。建立物理模型的过程是将问题的通用性语言描述转化为物理学科语言描述，进而揭示物理问题的本质，形成对一类（物理）问题共同属性的一般认识，这是提高物理习题课教学质量的一个重要途径。在日常习题课教学中，不重视对问题本质的揭示，就题论题，缺少变式与跟进，就会造成上课效率低下。因此，本文就如何在习题讲解过程中，准确建构物理模型，揭示物理问题的本质，并在此基础上提供变式与跟进策略抛砖引玉提些看法。

【关键词】 物理；物理模型；建构；变式

【中图分类号】 G63.26 【文献标识码】 A 【文章编号】 2095-3089（2017）16-0-02

一、物理模型与变式概述

物理模型，即在分析和解决实际物理问题时，突出主要的、本质的特征，忽略次要的、非本质的因素，对实际物体和物理过程所做的一种简化的描述或模拟。这是一种抽象的思维方法。以物理事实为基础，运用科学的思维方法，构建物理模型的过程是培养学生的创造思维和探索能力的有效途径。

变式，是变换同类事物的非本质特征，以便突出本质特征。在物理教学中运用变式可使学生更深刻地、牢固地理解物理概念与规律。通过变式变换同类事物的非本质特征，使非本质特征的种类既要全面，又要突出主要的、常见的，且遵循从简到繁、从易到难的原则。

二、建构物理模型，揭示物理问题本质

建构前：

如图所示，一开口向上的均匀玻璃管竖直放置，用一段水银柱封住一些气体，系统原来静止，当释放玻璃管的瞬间，玻璃管的加速度a管___________g（填“大于”、“等于”或“小于”），且以后玻璃管的加速度逐渐_________（填“增大”、“不变”或“减小”）

教师：

（1）研究的是玻璃管的加速度，所以我们应对玻璃管进行受力分析：

（2）对水银受力分析，玻璃管放手前水银受力平衡，a=0，放手后，a管>a汞，则空气柱体积将增大，压强减小，所以a管减小。

案例分析：

下课后，我对自己的授课感觉不满意，题目讲解后学生仍显得茫然。虽然我对问题的解决（示范）没有错，但为什么会出现收效不大的结果呢？从这里我们看到了教学的要义不仅在于教师对问题进行正确的诠释，更重要的是让教师对问题的诠释为学生所理解，并使他們获得个人意义。这就意味着习题课教学，重要的不是在于教师对问题的正确解答，而在于教师对问题诠释过程的组织，以利于学生的理解和内化。

那么教师如何组织对问题的诠释呢？我们先来剖析上述的教学片断：

在解决示范中，我直接进入了解决问题最后阶段——受力分析，然后运用牛顿第二定律分析获得结论。没有意识到对问题外显特征的归纳，引导学生通过对曾经解决过的问题进行筛选，提取与本问题具有共同外显特征的问题进行比较分析，从而使学生获得更普遍意义上的一般分析方法。这种就题论题的做法，可能就是习题课教学效率低下的一个普遍性症结。

而且，我在题目分析得出答案后，没提供变式跟进，以检测自己的讲评效果。这可能是低效习题课教学又一大特征。

三、物理模型建构与变式跟进策略

综上所述，物理模型建构与变式跟进可从以下三个方面进行提升：

提炼归纳，点面联系——建构一类问题的共同物理模型

分析问题，寻找关键——提示物理模型的本质属性

检测巩固，变式跟进——物理模型的迁移训练

建构后的变式提升设计：

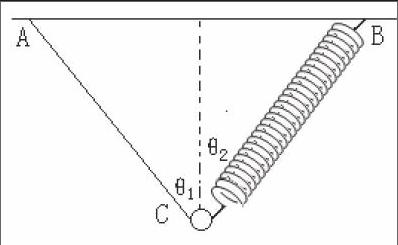
一轻弹簧，B端固定，另一端C与细绳共同拉住一个质量为m的小球，绳的另一端A固定，如图，AC、BC与竖直方向的夹角分别为θ1和θ2，则（ ）

（A）烧断细绳的瞬间上球的加速度为

（B）烧断细绳的瞬间上球的加速度为

（C）在C处弹簧与小球脱开瞬间小球的加速度为

（D）在C处弹簧与小球脱开瞬间小球的加速度为

教师：本题四个选项有什么共同的特征？

学生：“瞬间”。

教师：对，本题要求的就是细绳或弹簧与小球脱开“瞬间”加速度。请问求加速度需要应用什么知识？运用什么分析方法？

学生：牛顿第二定律，受力分析。

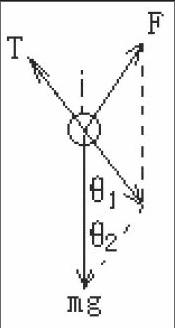
教师：画出烧断细绳之前的小球的（平衡）受力图，如右图。

教师：烧断之后瞬间，重力变吗？

学生：不变。

教师：弹簧弹力F变吗？

学生（部分）：不变。

教师：烧断绳子的瞬间，这两个力的合力怎么样？

学生：与未烧断前一样。

教师：边提示边板书，得出选项A。

然后指出在C处小球与弹簧断开的瞬间，小球将沿与绳垂直的方向作圆周运动，在受力分析的基础上，得出选项D。

变式跟进：

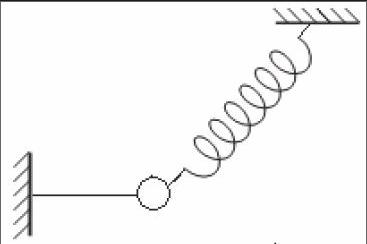
小球在水平和轻质弹簧（与竖直方向的夹角为θ）处于静止状态，求断开绳或者断开弹簧瞬间，小球的加速度。

当堂观察表明，部分学生较为顺利的解决了跟进的问题，但还有一些学生解决问题时存在困难。

案例反思：

我在新的设计中，强调了“弹簧在剪断轻绳前后的瞬间，其弹力因渐变的特性而保持不变，轻绳在小球脱离弹簧作用的瞬间，拉力可突变”这一类问题共同的特征，并试图提供变式以巩固学生对这一特征的应用操练，这是一种进步。但这种“进步”可能只是停留在表层，所提供的“变式”并不能说明学生是否已经形成“迁移”的能力，也许只是停留在模仿。

如，我想把既与弹簧相连同时又与轻绳相联的物体，作相同的物理模型，因为他们具有类似的结构和相同的处理方法。

思考我前一课时提供的竖直玻璃管一例与本课提供例子有没有相似之处？表面两种问题情境所呈现模型结构相去甚远，缺少类同。但两类问题情境提问的方式却有相似之处，处理問题的方法也有相似之处。

前者问的是“释放玻璃管的瞬间……”，后者问的是“剪断轻绳的瞬间……”。在处理方法上，前者气体对玻璃管的压力是渐变的，因而在释放玻璃管的瞬间，压力是不变；后者弹簧的弹力是渐变，因而剪断轻绳的瞬间，弹力是不变的。

所以这完全可以把它们归入同一物理模型。为突出这一物理模型的物理本质，我们可以给这一物理模型起个名，比如说这种在瞬间状态变化的问题命名为“瞬态变化”模型。

此外，我们也可以把用10N力竖直作用于浮在水面上两个物体的瞬间，求两物体间的作用力的问题归结到这一模型。并对这类模型为学生提供更具体解决思路，比如通过师生共同的活动，共同提炼这类问题共同特征，从而形成对这类问题的一般解决法。比如让学生通过对例题解答的全过程的提炼，获得对这类问题分析过程的如下认识：

问题的特征词：某个力消失的“瞬间”。

所求的特征：求这个“瞬间”的加速度。

解决过程的特征：这一瞬间前的受力分析。

分析的关键：某个力消失后，剩下的力是渐变力（如弹簧弹力，封闭气体压力、液体的浮力），还是突变力（细绳的拉力）？

解题的知识：牛顿第二定律。

至此，一个物理模型初步形成，其问题特征是求解状态变化瞬间的物理量，其分析的过程特征是由变化前的方程与变化后方程联立来求解问题，其关键点是把握“渐变量”在状态瞬间变化时保持不变。

假若教师在示范过程中，和学生一起对例题进行适当归纳，帮助学生认识上述物理模型的本质和特征，并提供适当变式（比如说将“10N的力作用于悬浮在水面上的两个物体的瞬间，求两物体间的作用力”作为上述例题的变式，让学生通过适当“迁移”自己纠正错误），相信教学会起到事半功倍的效果。

总之，在教学中，教师如果能有效地帮助学生从看似不同的问题情境中，寻找出共同的物理属性（这种属性可以是外形结构上的相似，也可以是涉及的物理知识和方法的相同，还可以是处理问题的思维方式的相似甚或数学表达的相似），指导学生学会建立相应的物理模型，并以此为依据为学生提供恰当的变式，将是提高物理习题教学有效性，引导学生形成问题分析、提高“迁移”能力的重要途径。

参考文献：

蒋明星《物理模型的建立及在教学中的作用》，《中小学教学研究》，2010（10）：32-33