水位下降条件下西安D7裂缝土体孔隙变化特征试验
2017-07-29段扬冯立胡伏生
段扬+冯立+胡伏生


摘要:为研究压缩性土体在孔隙水压力下降下所引起的孔隙变化特征,选取孔隙度及分形维数作为评判指标,以西安D7地裂缝两侧可压缩性土层为研究对象,借助三维CT扫描成像技术,依托Matlab计算平台及VG Studio Max图像处理软件,对在水位下降过程中可压缩性土体压缩变形引起的孔隙度和分形维数孔隙变化进行定量评价,并探讨了固结压缩过程中土体孔隙分形维数的变化规律及其影响因素。研究表明:孔隙度随压缩进行大幅降低,由压缩前4.36%降至0.61%;土体分形维数与孔隙度、上覆压力均呈线性相关性,相关系数分别为0.947 2和0.966 0;而且分形维数可以很好的表征孔隙分布特点,是孔隙度的有效补充;通过分析土样孔隙度与分形维数关系,为后期建立区域上地裂缝—地下水开采耦合模型提供参数赋值基础。
关键词:地面沉降;三维CT扫描;孔隙结构;孔隙分形模型
中图分类号:P642.2 文献标识码:A 文章编号:1672-1683(2017)04-0148-07
Abstract:In order to study the variation of compressive soil pores caused by decrease of pore water pressure,we studied the compressive soil on the two sides of the D7 ground fissure in Xi′an.Using the three-dimensional CT imaging technique,Matlab computing platform and VG Studio Max program,we calculated the porosity and fractal dimension variations caused by the compression deformation of compressive soil during the drop of water level,and discussed the influence factors and variation patterns of the porosity and fractal dimension in the consolidation process.The results showed that the porosity declined from 4.36% to 0.61% with the compression,and that the fractal dimension had a linear correlation with both the porosity and overburden pressure,at a correlation coefficient of 0.9237 and 0.9660 respectively.As an effective supplement of the porosity,fractal dimension could well represent the distribution characteristics of the pores.By analyzing the relationship between porosity and fractal dimension,the study results may provide parameter assignment basis for the fissure-groundwater pumping coupled model.
Key words:land subsidence;three-dimensional CT scanning;pore structure;pore fractal model
地裂縫、地面沉降作为一种地质灾害近年来对国民经济及社会发展所带来的损害正日渐显现出来。研究表明[1-3]:地面沉降、地裂缝与土体的变形特性和地下水的渗流特征密切相关。当地下水开采造成含水层孔隙水部分疏干后,黏性土中孔隙水也逐渐被排出,黏性土层和含水层孔隙水压力大幅度降低,土颗粒承担的应力大大增加,使土体产生固结压密。砂砾石含水层压缩变形以弹性变形为主,而黏性土层压密变形以弹塑性和塑性变形为主。同时表明,可压缩性土层的压密量与孔隙特征密切相关。由于土体作为典型多孔介质,其微观孔隙结构决定着孔隙度、毛细压力、相对渗透率等宏观特性,所以研究饱水多孔介质孔隙结构在孔隙水压力下降状态下所发生的变化对研究地面沉降、地裂缝的产生机理,建立点到面的孔隙发展模型,进而最终建立地裂缝—地下水开采耦合模型具有帮助作用。
近年来随着CT(计算机断层扫描)技术的发展,由于其能够无损探测物体内部结构和生成高密度分辨率横截面图像,被广泛应用多孔介质内部结构及损伤演化研究方面[4-8]。基于此,本文以西安D7地裂缝为研究对象,采用三维CT扫描手段和分形理论[9-10],开展地下水位下降过程中土体固结压缩的扫描实验,多梯度分级模拟水位下降过程中的孔隙发展规律,通过对CT图像的二次处理,揭示了土体压缩变形引起的土体孔隙特征的动态变化并探讨了变化规律以及影响因素,为进一步研究区域地下水开采引起的地面沉降、地裂缝的精确评价奠定理论基础。
1 地裂缝两侧土体概述
1.1 含水层划分及其实验土体
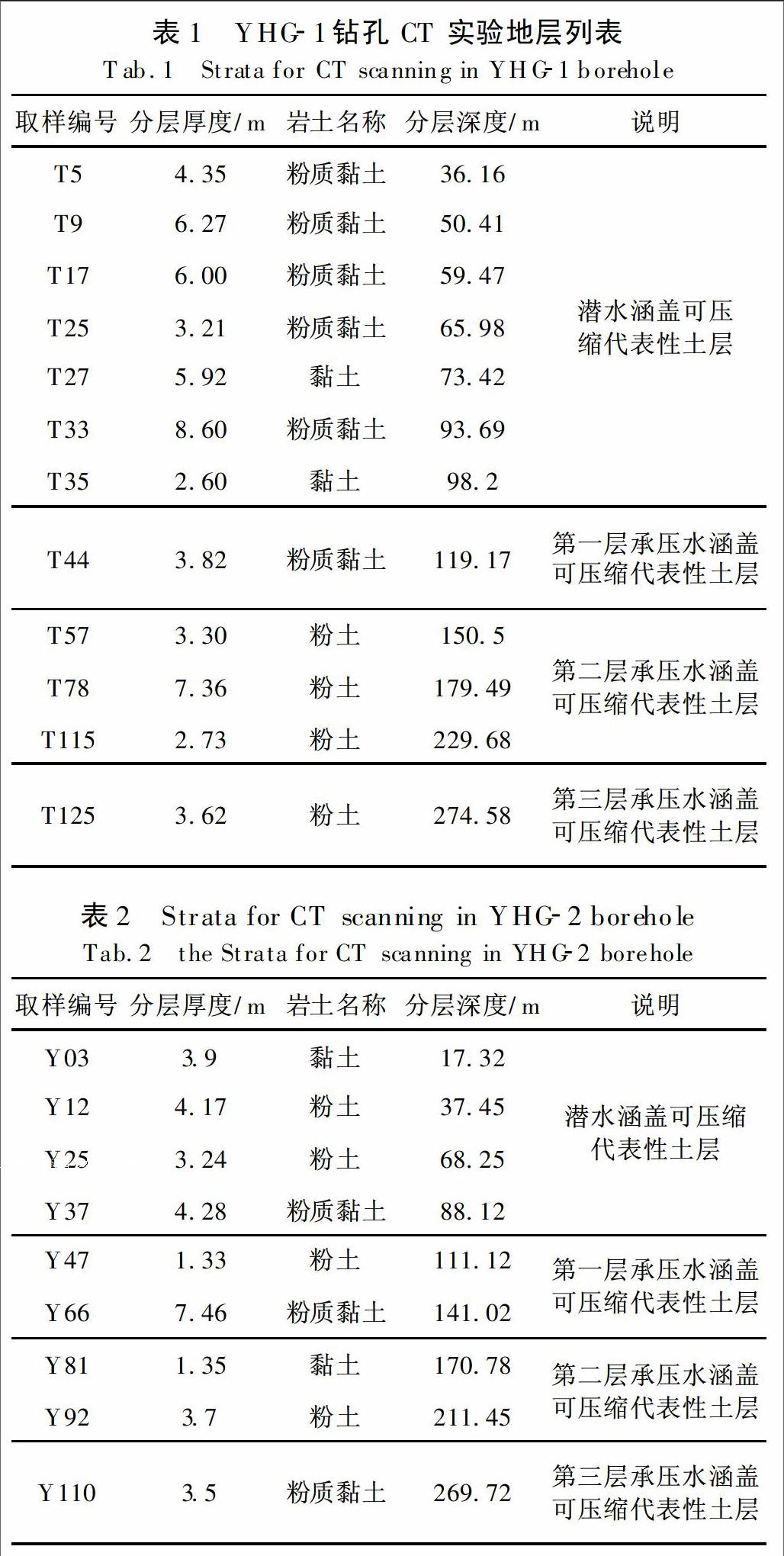
实验所用土样取自西安D7地裂缝鱼化寨附近南北两侧所打的2个工程地质钻孔,其中YHG-1位于地裂缝南侧即黄土洼地地区,YHG-2位于地裂缝北侧即黄土梁地区。YHG-1钻孔揭露深度为302.4 m,共划分为97个岩土层。其中砂层共29层,厚度为115.76 m,占比38%,黏性土分为58层,厚度为186.64 m,占比为62%;YGH-2钻孔揭露深度为302.3 m,共分为139层。其中砂层共37层,厚度为110.42 m,占比为36.52%,黏性土层共102层,厚度为191.88 m,占比为63.48%。根据钻孔记录二钻孔揭露地层均可划分为潜水及三层承压水。考虑到本区地面沉降为抽取承压水引起,主要压密地层为粉土层、粉质黏土层和黏土层,故本次设计CT扫描实验主要为剖面深度范围内,水位线以下的粉土、黏土及粉质黏土地层。共选取了22个代表性地层取样并进行三维岩石CT扫描来观察抽取地下水过程中土体孔隙变化,详见表1、2。
1.2 实验仪器及方法
本次实验采用XTH 320 LC型扫描仪,其集工业X射线和CT系统于一身,可以无损伤的以二维断层图像或三维立体图像的形式,清晰、准确、直观地检测物体内部的结构、组成、材质及缺损状况[14]。其主要由320 kv 级铅房、320 kv 微焦点射线源、5轴可编程操控系统CT样品台、手动摇杆控制和交互式计算机控制系统以及装备有“Inspect-X”检测-控制软件的工作站五部分组成。
试件采用φ20 mm×25 mm的圆柱体,CT加速电压为100 KV,功率18.6 W,扫描焦距为960 mm,分辨率为 3 μm,放大倍数为13倍,投影数为3 000张。
实验过程为:首先将土样饱和并进行一次扫描;之后在排水条件下缓慢恢复上覆压力,记录变形与时间数据,进行第二次扫描;自然排水完成后,加载压力,分阶段扫描,直至达到设计压力。本次设计压力设定为水位线与该层土体底板重合。稳定标准为连续2 h变形量小于1 mm,最后卸荷回弹,记录回弹曲线。考虑到地下水位下降是一个缓慢的过程,所以本次实验设计时根据土体埋深情况逐级增加压力直至最大设计压力,其中对于埋深较深的土体最多分4次加压,加上初始扫描共进行5次CT扫描, 22个土样最终共进行75次扫描。
2 图像处理
2.1 图像扫描
为避免土样制备过程中人为因素所引入的次生孔隙、裂隙对最终计算结果所带来的影响,在试样中部重新选取一个φ10 mm×15 mm的圆柱形区域进行结果统计,在XYZ方向分别进行切片,每个方向切片数为20,共60张扫描照片,切片图像为2 572×2 572像素的16位TIFF图像,灰度范围为0~65 535,见图1。
CT图像的成像原理是将选定层面分为若干个体素并记录下每个体素的X射线衰减系数并排列为数字矩阵,之后将矩阵中的每个数字转为由黑到白不同灰度的像素并按矩阵排列。每个像素的灰度值代表该处的物质密度[11],其中像素呈黑色表明物质密度低,反之密度高。具体到图1可看出灰色代表土体固体颗粒,黑色代表孔隙空间。
考虑到在原始图像四周的颜色为扫描图像时系统直接附加而成,对于最终计算会产生严重地干扰,为便于后续图像处理,在图片中部设置一固定大小的矩形区域,仅对该区域进行统计计算,有助于消除试样边缘的伪像区。
2.2 孔隙确定
获取CT图像后,对图像灰度值进行阈值分割,将低于阈值像素认为是孔隙并将其灰度值重新赋值为0,而将高于阈值像素认为是固体颗粒并将其灰度值设为1,以此实现了图像的二值化,通过统计灰度值为0的像素单元数以及总像元数可得到单张图像的面孔隙度:
但是传统方法会存在以下不足:(1)阈值需要人为给定并进行多次试算,而这一过程受制于实验者的经验,存在有一定的随机性及不确定性。(2)仅仅通过灰度值大小来判断是否为孔隙并不准确,因为诸如扫描参数的变化都会影响灰度值的大小,其仅能相对反映各体素密度的大小。
基于上述问题,为了准确的研究出土样中的孔隙结构,需首先对扫描土样利用VG Studio Max软件进行孔隙识别操作。其可以通过基于感兴趣区(ROI)的缺陷掩模算法将分析参数应用到ROI的每个体素组,通过导入ROI模版来区别真实的孔隙和伪像,并用概率阈值来表征。在检测潜在孔隙的同时与其邻域进行比较,如果潜在孔隙外观与周围结构相似,则会降低其概率值,可以有效的减少伪像的数量。经过孔隙检查后可以将孔隙大小和位置通过颜色云图的方式显现出来,见图2。本次实验仅考虑概率值大于1且体积大于64体素(0.000 2 mm3)的孔隙。
由于方差是灰度值分布的度量,一旦出现前景与背景错分势必造成类间方差的缩小,因此类间方差值达到最大表明错分概率最小。利用Matlab进行编程求解二分阈值可以在保证准确性的前提下避免多次试算,提高计算效率。
在求解过程中发现,Otus法对于存在大量较大孔隙的图像识别率较高,而对于小孔隙较多的图像识别度较差,见图3(b),绝大部分区域被误认为孔隙,与实际偏差较大。从灰度直方图中也可看到绝大部分像素点都落在70~95附近,另有一少部分落在225附近,致使算出的阈值落在二者中间,而实际上绝大部分像素点均为背景色,算法对于前景色和背景色识别出现了偏差。为了避免这种问题,将上一步VG Studio Max软件所输出的切片图像在Photoshop中转化为16位的RGB图像,并对其黑白对比度进行调整,选择纯黑,见图3(d),可以看出孔隙部分被明显加深,与周围像素的对比度增大,从灰度直方图中也可看出在灰度值为0处出现了大批像素点,使得计算阈值大大缩小,由0.624 5下降为0.164 7,准确的将孔隙部分勾勒出,所计算出的面孔隙度为5.68%,并与所计算的真实孔隙度进行对比,误差较小。
到的结果可信度高,所计算出的分形维数为1.385。
图5为不同迭代次数下图像分形维数变化图,从图中可以看到,随着迭代次数的增加,分形维数呈线性下降趋势,从迭代30次时的1.493下降到迭代80次时的1.350,下降幅度为9.39%。主要原因在于当盒子尺寸较大时,包含有孔隙的可能性加大,使得相应尺寸下的盒子数目的减小趋势变低,反映在双对数图像上即直线段的斜率降低,分形维数下降。
3.2 基于孔隙度的分形模型建立
由于分形维数反映的是孔隙填充土壤界面的方[CM(22]式,当分形维数D越大时,表明当盒子尺寸逐步减小时,所观察到的土壤固体颗粒消失的速度越慢,反之当D越小时,其消失速率越快,所以D反映的孔隙對于土壤切面的覆盖度,即孔隙度的大小[15]。
图6为Y81号土样中Z方向同一切片图像在抽取地下水状态下不同降深下的孔隙分布图。
由于抽取地下水作用,使得孔隙水压力降低,根据Terzaghi有效应力原理,有效应力等于上层总应力减去孔隙水压力,当抽取地下水导致地下水位下降时,孔隙水压力u0降低,竖向总应力e不变使得作用在土体颗粒上方的有效应力e′增加,土体受到比以前更大的垂向压力,土体出现压缩变形,宏观表现出沉降,孔隙出现压密,从图6中可以显现出来随着抽取地下水的进行,土体的孔隙体积出现了明显的减少,直观反应在孔隙度中表现为孔隙度降低,由未抽水时的4.36%缩小到最终状态的0.61%,减小幅度为86%。
可以看出,在各个方向上孔隙度与分形维数都有着一定的正相关性,其平均的相关系数为0.988,传感器读数也与分形维数具有良好的相关度,平均相关度也达到了0.966。随着孔隙度的减小以及传感器压力的增大,孔隙结构的分形维数出现了减小。对比图6的切片图像也可以看出,当未抽取地下水时,孔隙结构较为复杂,大大小小孔隙交错分布,对应的分形维数也较大;而随着地下水的开采使得上覆压力的增加大量孔隙消失,其复杂程度也明显下降,其分形维数也有了较大幅度的减小。如果考虑Y81土样全部20个切片,则其XYZ方向的分形维数其平均衰减率为12.8%,8.38%,10.47%;相应孔隙度的平均衰减率为76.00%,79.96%,79.24%;分形维数与孔隙度间的相关系数为0.923 8,0.942 2,0.975 6。说明分形维数D可以很好的定量描述土体的孔隙特征,客观的反映土体在抽水情况下的孔隙结构变化,而且这种对应关系与方向性关联不明显。
然而影响分形维数变化的因素绝非仅有孔隙度一个,在实际计算过程中发现一些切片的孔隙度较为接近,但其分形维数却相差较大。图8(a)所示切片其孔隙度为0.69%,分形维数为1.318,图8(b)其孔隙度为0.70%,但分形维数仅为1.180。可以看出图8(a)中孔隙分布较为分散,大孔隙极少,主要为微细孔隙;而图8(b)中主要以大孔隙分布为主,其孔隙结构复杂程度要远小于图8(a),所以分形维数不仅可以体现孔隙度的大小,也能指示孔隙的复杂程度。
4 结论
基于西安地裂缝与地面沉降主要是由于开采地下水所引发的差异沉降所致,本文依托三维CT成像技术对D7地裂缝两侧22个土样模拟水位下降条件下进行了75次扫描分析,较为真实地反映孔隙介质的结构特征及空间分布,并依托图像处理软件及Matlab数学计算平台进行处理分析。
(1)经过压缩后,无论从孔隙数目和大小上都出现了明显下降,孔隙度从为压缩时的4.36%下降为0.61%,下降幅度为86%。
(2)建立了基于Otus最大类间方差法的阈值分割算法,可以快速准确的确定二值化图像分割阈值,避免了人工试算阈值的繁缛及不确定性。
(3)通过使用VG Studio Max软件进行孔隙识别前处理之后再进行图像二值化,可以准确的区分真实孔隙和伪像并进行标注,并通过Photoshop对图像对[HJ1.7mm]比度进行调整,使得所计算出的孔隙度真实准确。
(4)利用盒维法原理通过MATLAB进行孔隙分形维数的确定,之后对西安地裂缝两侧土样进行计算,发现对于同一张扫描照片来讲,分形维数与迭代次数(盒子最大尺寸)呈负相关关系。孔隙分形维数随着孔隙度增大而增大,XYZ方向二者之间的相关系数分别为0.923 8,0.942 2,0.975 6,相关性较强。此外,分形维数与传感器读数也有着较好的负相关关系,相关系数为0.966,反映出随着抽取地下水的进行,孔隙水压力不断降低,有效应力不断增加,孔隙不断被压密缩小,使得孔隙度和分形维数均大大下降。
(5)分形维数除受孔隙度影响外,还受孔隙分布复杂程度影响,当孔隙结构越復杂,其分形维数越大。分形维数可以很好的表征孔隙分布特点,是孔隙度的有效补充。通过分析土样孔隙度与分形维数关系,为后期建立地裂缝—地下水开采耦合模型时参数赋值提供帮助。
参考文献(References):
[1] 李勤奋,方正,王寒梅.上海市地下水可开采量模型计算及预测[J].上海地质,2000,23 (2):36-43.(LI Qin-fen,FANG Zheng,WANG Han-mei.A mathematical model and foecast of groundwater workable reserves for Shanghai[J].Shanghai Geology.2000,23(02):36-43.(in Chinese))
[2] 张利生,朱国荣.鹏山水源地开采条件下的含水层固结模型[J].岩土力学,2005,26 (7):1141-1147.(ZHANG Li-sheng,ZHU Guo-rong.Consolidation model of aquifer under pumping condition at Pengshan water well field[J].Rock And Soil Mechanics,2005,26(7):1141-1147.(in Chinese))DOI:10.3969/j.issn.1000-7598.2005.07.028
[3] 朱桂娥,薛禹群,李勤奋,等.上海市多层结构地下水系统准三维模型的改进[J].中国岩溶,2000,19(4):31-36.(ZHU Gui-e,XUE Yu-qun,LI Qin-fen et al.The improvement of quasi-three dimensional model of multi-aquifer ground water system in Shanghai[J].Carsologica Sinica,2000,19(4):31-36.(in Chinese))DOI:10.3969/ j.issn.1001-4810.2000.04.005
[4] 徐宗恒,徐则民,李凌旭.基于CT扫描的斜坡非饱和带土体大孔隙定量化研究和三维重建[J].水土保持通报,2015,35 (1):133-138.(XU Zong-heng,XU Ze-min,LI Ling-xu.Soil macropores quantification study and 3D reconstruction in vadose zones of hillslope based on x-ray computed tomography[J].Bulletin of Soil and Water Conservation,2015,35(1):133-138.(in Chinese))
[5] 袁则循,毛灵涛,彭瑞东,等.CT孔隙岩石内部三维变形场数字实验[J].辽宁工程技术大学学报:自然科学版,2014(8):1080-1085.(YUAN Ze-Xun,MAO Ling-tao,PENG Rui-dong,et al.Digital experimental on internal three dimensional deformation field measurement of porous rock based on computer tomography[J].Journal of Liaoning Technical University,2014,33(8):1080-1085.(in Chinese))
[6] 李玉彬,李向良,高岩.用微焦点X-CT成象研究岩石微观特征[J].油气地址与采收率,2000,7(4):50-52,50.(LI Yun-bin,LI Xiang-liang,GAO Yan.Study of microscopic rock feature using microfocus X-CT imaging[J].Petroleum Geology and Recovery Efficiency,2000,7(4):50-52,50.(in Chinese))
[7] 屈乐,孙卫,杜环虹,等.基于CT扫描的三维数字岩心孔隙结构表征方法及应用——以莫北油田116井区三工河组为例[J].现代地质,2014,28(1):190-196.(QU Le,SUN Wei,DU Huan-yu,et al.Characterization technique of pore structure by 3d digital core based on CT scanning and its application:An example from sangonghe formation of 116 well field in mobei oilfield[J].Geoscience,2014,28(1):190-196.(in Chinese))
[8] 苏娜,段永刚,于春生.微CT扫描重建低渗气藏微观孔隙结构——以新场气田上沙溪庙组储层为例[J].石油与天然气地质,2011,32(5):792-796.(SU Na,DUAN Yonggang,YU Chunsheng.Reconstruction of microscopic pore structure in low permeability gas reservoirs by micro-CT scanning:an example from the Upper Shaximiao Formation in Xinchang gas field[J].Oil & Gas Geology,2011,32(5):792-796.(in Chinese))
[9] 刘俊亮,田长安,曾燕伟,等.分形多孔介质孔隙微结构参数与渗透率的分维关系[J].水科学进展,2006,17(6):812-817.(LIU Jun-liang,TIAN Chang-an,ZENG Yan-wei,et al.Fractal dimensionality dependence of microstructural parameters and permeability in fractal porous media[J].Advances in Water Science,2006,17(6):812-817.(in Chinese))DOI:10.3321/j.issn:1001-6791.2006.06.010
[10] 毛灵涛,薛茹,安里千,等.软土孔隙微观结构的分形研究[J].中国矿业大学学报,2005,34(5):600-604.(MAO Ling-tao,XUE Ru AN,Li-qian,et al.Fractal approach on soft soil porosity microstructure[J].Journal of China University of Mining & Technology,2005,34(5):600-604.(in Chinese))DOI:10.3321/j.issn:1000-1964.2005.05.012
[11] 崔玉柱,陈浩,李世根.基于ICT技术的微裂纹检测[C].第十三届中国体视学与图像分析学术会议[A].山西太原,2013.(CUI Yu-zhu,CHEN Hao,LI Shi-gen.Detecting Micro-crack of different material based on ICT[C].The 13th Academic conference on stereo vision and image analysis[A].TaiYuan,2013.(in Chinese))
[12] 李建胜,王东,康天合.基于显微CT试验的岩石孔隙结构算法研究[J].岩土工程学报,2010,32(11):1703-1708.(LI Jian-sheng,WANG Dong,KANG Tian-he.Algorithmic study on rock pore structure based on micro-CT experiment[J].Chinese Journal of Geotechnical Engineering,2010,32(11):1703-1708.(in Chinese))
[13] 韓青松,贾振红,杨杰,等.基于改进的Otsu算法的遥感图像阈值分割[J].激光杂志,2010,31 (6):33-34.(HAN Qing-song,JIA Zhen-hong,YANG Jie,et al.Remote sensing image thresholding segmentation based on the modified Otsu algorithm[J].Laser Journal,2010,31(6):33-34.(in Chinese))DOI:10.3969/j.issn.0253-2743.2010.06.018
[14] 张肖宁,孙杨勇.岩石表面纹理的分形维数计算[J].计算机工程,2010,36(23):277-279.(ZHANG Xiao-ning,SUN Yang-yong.Fractal dimension calculation for rock surface texture[J].Computer Engineering,2010,36(23):277-279.(in Chinese))DOI:10.3969/j.issn.1000-3428.2010.23.093
[15] 彭瑞东,谢和平,鞠杨.二维数字图像分形维数的计算方法[J].中国矿业大学学报,2004,33(1):22-27.(PENG Rui-dong,XIE He-ping,JU Yang.Computation method of fractal dimension for 2-D digital image[J].Journal of China University of Mining & Technology,2004,33(1):22-27.(in Chinese))DOI:10.3321/j.issn:1000-1964.2004.01.005.
[16] 黄丽.饱和软黏土微观孔隙的定量分析及其分形研究[D].武汉:武汉理工大学,2007.(HUANG Li.Quantitative analysis of micro-porosity of saturated soft clay and its fractal description[D].Wuhan: Wuhan University of Technology,2007.(in Chinese))
