基于TOPSIS—模糊综合评判的模糊推理模型在开河预报中的应用

雷冠军+殷峻暹+刘惠敏+张丽丽

摘要：冰凌开封河受到较多自然和人为因素的影响，具有较高的不确定性，为了进一步提高冰凌开封河预测的精度，考虑各因素的综合作用成为解决问题的关键。先采用主成分分析法初步确定冰凌开封河历时影响因子的权重，运用模糊推理模型依据影响因子矩阵的相似性进行初步预测，进而采用TOPSIS-模糊综合评判模型对预报因子进行识别，筛选出合理的预报因子进行二次预测。运用实例对基于TOPSIS-模糊综合评判模型冰凌预报因子识别的模糊推理模型的效果进行了检验，同时与冰凌预报模糊优选神经网络BP模型进行对比，结果表明：在TOPSIS-模糊综合评判模型因子进行识别基础上的模糊推理模型预测精度较高、效果较好，既能够有效识别预报因子，又能够较好地提高预报封河、开河历时的精度，为凌汛预测提供了新的途径。

关键词：模糊推理；主成分分析法；TOPSIS-模糊綜合评判；凌汛

中图分类号：P338；TV882 文献标识码：A 文章编号：1672-1683（2017）04-0007-06

Abstract：The break-up and freeze-up of the river is under the influence of various natural and human factors，and is an issue of great uncertainty.To further improve the accuracy of break-up and freeze-up forecasts，the key is to consider the combined action of various factors.First，we used the principal component analysis to preliminarily determine the weight of each factor that affects the break-up and freeze-up duration，and used the fuzzy reasoning model to conduct preliminary prediction according to the similarity of the impact factor matrix.Then we identified forecast factors using the TOPSIS-fuzzy comprehensive evaluation model and selected reasonable forecast factors to conduct secondary prediction.The fuzzy reasoning model based on TOPSIS-fuzzy comprehensive evaluation and ice forecast factor identification was tested in a case study and was compared with the fuzzy optimization neural network BP model.The results showed that the fuzzy reasoning model in this paper had high precision and good effects in prediction.It can effectively identify forecast factors，and can well improve the accuracy of freeze-up and break-up duration forecasts.It provides a new approach for ice run prediction.

Key words：fuzzy reasoning；principal component analysis；TOPSIS-fuzzy comprehensive evaluation；ice run

1 模糊推理预测模型

中长期径流预报的模糊推理预测模型能够综合考虑径流过程较多的复杂的影响因素。冰凌开封河影响因素复杂，因而开封河预报模型预报因子较多，为了综合考虑预报因子对冰凌开封河的影响，采用模糊推理预测模型，根据冰凌开封河与多个预报因子之间的相关关系综合预测，能够在获得预报结果的同时得出预测结果的不确定性，为管理者决策提供依据。模糊推理预测模型以预报因子级别特征值作为输入，采用加权法计算待预报因子与预报因子之间的相似关系，选取相似关系最大的预报因子系列对应的开河日期作为输出，输出值即为待预报因子所对应的开河日期。

模糊推理预测模型权重的确定采用主成分分析法，该方法是研究如何用多个指标（因子）来描述研究单位（个体）的一种统计分析方法，把原来多个彼此相关的指标（原变量）线性组合为少数几个彼此独立的综合指标（新变量），它提取出原指标主要成分的统计信息，能够有效反映该指标值个体的变异。

4.3 误差评定与优选判别

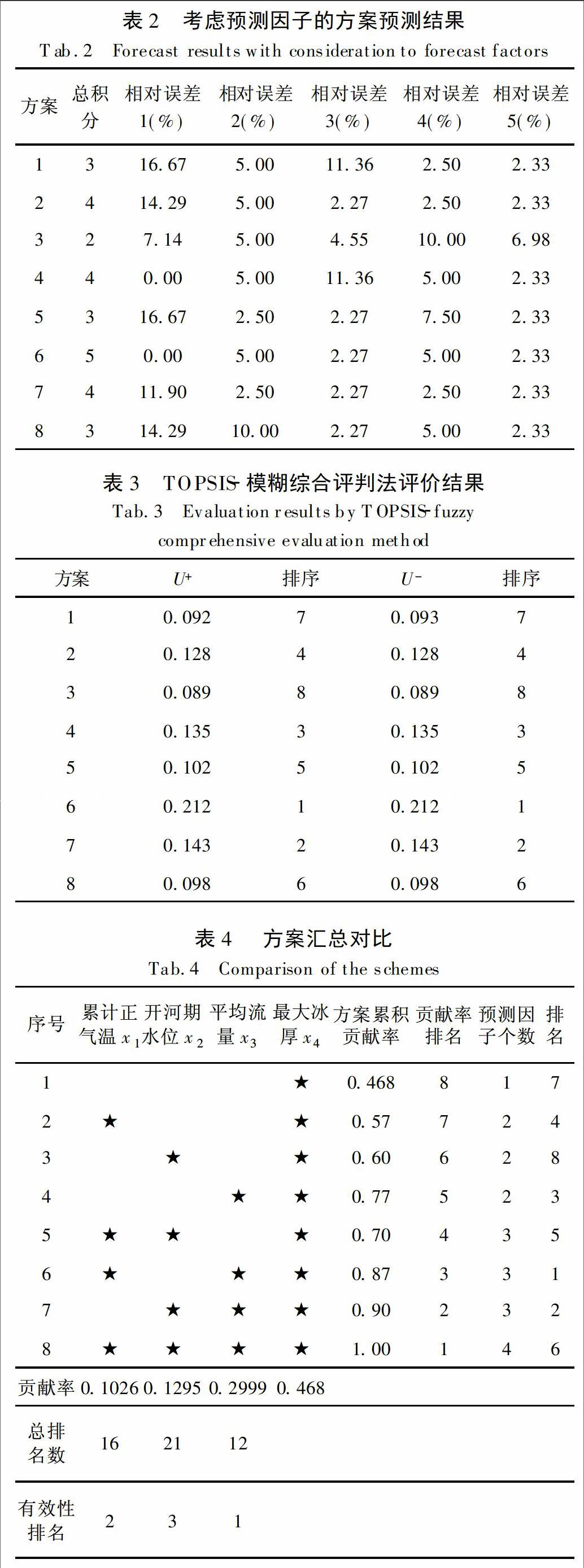
由评分法和相对误差法建立判断矩阵，结果见表2，运用TOPSIS-模糊综合评判法进行评判，评判结果见表3。将预测值的评价结果综合列于表4，为了说明累积贡献率和因子个数在挑选因子组合方案时的作用，由表4作出预测结果的排名与因子个数和累积贡献率的关系图。

相对误差1代表第一个预测年份即1996年-1997年在各个组合方案中的相对误差。以次类推。

总排名数为该因子所在方案排名之和，总排名越靠后，说明该因子的预测结果的精度越低，即因子的有效性越差。最大冰厚因子x1累积贡献率最大，各个方案均予以考虑，不再计算其总排名数。

本文在采用TOPSIS-模糊綜合评判法对影响因子进行筛选识别后，采用模糊推理法对开封河历时进行预报，与陈守煜、冀鸿兰[3]运用模糊优选神经网络BP模型进行预报的结果对比表明，基于TOPSIS-模糊综合评判法冰凌预报因子识别的模糊推理模型的5个预测值的误差都在误差允许范围内，相对误差较小，预报结果精度大大优于模糊优选神经网络模型，对比结果见表5。

4.4 结果分析

（1）冰凌开封河历时是个多因子综合作用的过程，由表4、图1可知，单一考虑最大冰厚因子，所得到的预测结果排名在第7位，考虑最大冰厚因子与其他因子相结合的方案，有6个排在前6位，说明冰凌开封河预报历时应该考虑多个因子的影响。

（2）冰凌开封河历时预测的影响因子根据累积贡献率初步确定后应进一步筛选：由表4、图1可知，方案7、方案6的累积贡献率大于方案5，而方案5的精度却是最好的，同时方案累积贡献率的排名和预测结果精度的排名并没有对应关系，说明累积贡献率确定后因子组合方案还需进一步识别才能确定最优的方案。

（3）累积贡献率相近的因子组合需进一步深入探讨：通过方案2，方案3和方案6，方案7的对比发现，累积贡献率相近的情形下，需要综合评价因子组合以进一步找到最佳的预测因子组合。

5 结语

冰凌开封河历时预测精度关系到防凌减灾工作的开展，直接关系到人民生命财产安全。冰凌开封河历时受到众多影响因素的制约，传统的预测方法不能对影响因子进行有效地识别，大大限制了冰凌预测的工作精度的提高。本文提出的基于TOPSIS-模糊综合评判法冰凌预报因子识别的模糊推理模型能够在对预报因子进行识别的基础上，运用合理因子建立模型对冰凌开封河历时进行预报，与模糊优选神经网络BP模型相比精度有了极大的提高，为凌汛预报提供了一个新的有效途径。

参考文献（References）：

[1] 刘吉峰，杨健，霍世青，等.黄河宁蒙河段冰凌变化新特点分析[J].人民黄河，2012，34（11）：12-14.（LIU Ji-feng，YANG Jian，HUO Shi-qing，et al.Analysis on some new ice characteristics in Ningxia-Inner Mongolia reach of the Yellow River[J].Yelow River，2012，34（11）：12-14.（in Chinese））DOI：10.3969/j.issn.1000-1379.2012.11.004

[2] 可素娟，王敏，饶素秋，等.黄河冰情研究[M].郑州：黄河水利出版社，2005.（KE Su-juan，WANG Min，RAO Su-qiu，et al.The Yellow River ice stdy[M].Zhengzhou：The Yelow River Conservancy Press，2005.（in Chinese））

[3] 陈守煜，冀鸿兰.冰凌预报模糊优选神经网络BP方法[J].水利学报，2004，35（6）：114-118.（CHEN Shou-yu，JI Hong-lan.Fuzzy optimization neural network BP approach for ice forecasting[J].Journal of Hydraulic Engineering，2004，35（6）：114-118.（in Chinese））DOI：10.3321/j.issn：0559-9350，2004.06.020

[4] 王涛，杨开林，郭永鑫，等.神经网络理论在黄河宁蒙段冰情预报中的应用[J].水利学报，2005，36（10）：1042-1208.（WANG Tao，YANG Kai-lin，GUO Yong-xin，et al.Appication of artificial neural networks to forecasting of river ic condition.Journal of Hydraulic Engineering，2005，36（10）：1042-1208.（in Chinese））

[5] 张傲妲.黄河内蒙段冰情特点及预报模型研究[D].呼和浩特：内蒙古农业大学，2011.（ZHANG Ao-da.Research on the characteristics and the prediction model of ice regime in the Inner Mongolia Reach of the Yellow River[D].Hohhot：Inner Mongolia Agricultural University，2011.（in Chinese））

[6] 冀鸿兰，张傲妲，高瑞忠，等.黄河内蒙古段开河日期预报模型及应用[J].水利水电科技进展.2012，4，32（2）：42-45.（JI Hong-lan，ZHANG Ao-da，GAO Rui-zhong，et al.Application of the break up date prediction model in the Inner Monglia Reach of the Yellow River[J].Advances in Science and Techology of Water Resources，2012，4，32（2）：42-45.（in Chinese））DOI：10.3880/j.issn.1006-7647.2012.02.010

[7] 徐晶，冀鸿兰，张宝森，等.基于可变模糊综合分析的冰凌预测模型[J].水利水电科技进展，2011，31（3）：6-8，26.（XU Jing，JI Hong-lan，ZHANG Bao-sen.Ice forecast model based on variabe fuzzy synthetic analysis[J].Advances in Science and Techology of Water Resources，2011，31（3）：6-8，26.（in Chinese））DOI：10.3880/j.issn.1006-7647.2011.03.002

[8] 赵晓慎，李倩，王文川.基于成因综合分析的冰凌预测模型[J].人民黄河，2011，33（1）.（ZHAO Xiao-shen，LI Qian，WANG Wen-chuan.The ice prediction model based on the general analysis of the causes[J].Yellow River，2011，33（1）.（in Chinese））

[9] 韩宇平，蔺冬，王富强，等.基于粒子群算法的神经网络在冰凌预报中的应用[J].水电能源科学，2012，30（3）.（HAN Yu-ping，LIN Dong，WANG Fu-qiang，et al.Application of neural networks to ice forecasting based on particle swarm optimization[J].Water Resources and Power，2012，30（3）.（in Chinese）） DOI：10.3969/j.issn.1000-7709.2012.03.011

[10] [ZK（#]陈守煜，薛志春，李敏，等.基于可变集的年净流预测方法[J].水利学报，2014，45（8）.（CHEN Shou-yu，XUE Zhi-chun，LI Min，et al.Annual runoff prediction method based on the variable sets[J].Journal of Hydraulic Engineering，2014，45（8）.（in Chinese））

[11] 李敏.可变模糊近似推理方法在径流中长期预报中的应用[J].水电能源科学，2010，28（2）：16-18.（LI Min.Variable fuzzy approximate reasoning metthod and its application in mid and long term runoff forecasting[J].Water Resources and Power，2010，28（2）：16-18.（in Chinese）） DOI：10.3969/j.issn.1000-7709.2010.02.006

[12] 王永县，朱涛，李飞.基于相似关系的广义近似推理方法[J].清华大学学报：自然科学版，2002，42（10）：128-1288，1308.（WANG Yong-xian，ZHU Tao，LI Fei.General similarity-based approximate reasoning method[J].Journal of Tsinghua University：Natural Science，2002，42（10）：128-1288，1308.（in Chinese））DOI：10.3321/j.issn：1000-0054.2002.10.004

[13] 陳守煜.基于可变模糊集的辩证法三大规律数学定理及其应用[J].大连理工大学学报，2010，50（5）：838-844.（CHEN Shou-yu.Three mathematical theorems of dialectics based on variable fuzzy sets and their application[J].Journal of Dalian University of Technology，2010，50（5）：838-844.（in Chinese））

[14] 王文川，徐冬梅，陈守煜，等.可变模糊集理论研究进展及其在水科学中的应用[J].水利水电科技进展，2012，32（5）：89-94.（WANG Wen-chuan，XU Dong-mei，CHEN Shou-yu，et al.Research Advances and application in water science of variable fuzzy set theory[J].Advnces in Scienc and Technology of Water Resources，2012，32（5）：89-94.（in Chinese））D OI：10.3880/j.issn.1006-7647.2012.05.023

[15] 傅湘，纪昌明.区域水资源承载能力综合评价-主成分分析法的应用[J].长江流域资源与环境，1999（2）：168-173（FU Xiang，JI Chang-ming.A comprehensive evaluation of the regional water resource carrying capacity[J].Resources and Environment in the Yangtze River，1999（2）：168-173 （in Chinese））

[16] 盛周君，孙世群，王金城，等.基于主成分分析的河流水环境质量评价研究[J].环境科学与管理，2007，32（12）：172-175.（SHENG Zhou-jun，SUN Shi-qun，WANG Jin-cheng，et al.Comprehensive evaluation of river water environmental quality based on the principal component analysis[J].Environmental Science and Management，2007，32（12）：172-175.（in Chinese）） DOI：10.3969/j.issn.1673-1212.2007.12.052

[17] 欧阳铭，白若男，朱国宇.成都市水资源承载能力动态变化及成因[J].南水北调与水利科技，2012（6）：110-114.（OUYANG Ming，BAI Ruo-nan，ZHU Guo-yu.Dynamic variation of water resources carrying capacity and its causes in Chengdu[J].South-to-North Water Transfers and Water Science & Technology，2012（6）：110-114.（in Chinese））

[18] 雷冠军，王文川，刘宽，等.TOPSIS-模糊综合评判法在优选水文频率参数估计方法中的应用[J].水资源研究，2015（4）：200-207.（LEI Guan-jun，WANG Wen-chuan，LIU Kuan，et al.The application of the TOPSIS-fuzzy comprehensive evaluation method used in the method of optimizing the hydrologic frequency parameter estimation[J].Journal of Water Resources Research，2015（4）：200-207.（in Chinese））

[19] 张晓华，毕生，曹永潇.基于TOPSIS法的陕西省黄河流域干旱综合评价模型[J].南水北调与水利科技，2015（2）：211-213.（ZHANG Xiao-hua，BI Sheng，CAO Yong-xiao.Comprehensiveevaluation model model of drought in the Yellow River of Shaanxi province based on TOPSIS method[J].South-to-North Water Transfers and Water Science & Technology，2015（2）：211-213.（in Chinese））

[20] 许峰，秦成.地下水环境质量评价—基于粗糙集理论和灰色关联系数矩阵的TOPSIS模型[J].南水北调与水利科技，2015（6）：1097-1100，1109.（XU Feng，QIN Cheng.Evalation of groundwater environment quality based on rough set and TOPSIS method gray correlation coefficient matrix[J].South-to-North Water Transfers and Water Science & Technology，2015（6）：1097-1100，1109.（in Chinese））