引导学生充分经历知识的形成过程

朱国荣

【编者按】学生只有充分经历知识的形成过程，才能生成属于自身的新认知、新体验与新收获，而且要经历充分的分享与交流才能展现出它们最大的作用。如何在课程教学中确保学生经历知识形成的全过程，让学生乐于交流分享，相应教学环节不浮于形式？本期话题围绕经历知识形成，敢于分享交流，打造新型数学课堂展开探讨。

学生只有充分经历知识的形成过程，才能确保生成属于他们自身的新认知、新体验与新收获，而这些是学生能够，也乐于进行分享交流的坚实基础。本文将以人教版三年级上册中的分数、毫米（分米）、倍、四边形等概念的教学为例，阐述如何引导学生充分经历知识的形成过程。

一、链接生活，借助生活前概念引导学生建立数学概念

三年级上册是小学阶段首次教学分数概念，这是在学生认识了整数概念的基础上进行教学的。但从整数概念到分数概念，是学生数概念认识上的一次飞跃，引导三年级学生掌握分数概念是一件较为困难的事。整数（自然数）是表示物体个数的数，但在分物时，如果只有1个物体（比如1块月饼），但要平均分给2人，这时每人分得的月饼数量就不到1块，生活中一般说成“半块”；如果平均分给3人，就说每人分得“小半块”；如果平均分给4人，就说每人分得“半块的半块”。生活中所说的“半块”“小半块”“半块的半块”是学生学习分数的生活前概念，分别对应1/2块、1/3块、1/4块。通过以上分析，我们可以确定分数初步认识教学的基本路径，即创设分月饼的情境，引导学生先借助生活前概念分别表示将1块月饼平均分给2人、3人、4人后每人分得的数量，然后引导和鼓励学生进行数学的再创造，要求学生用数分别表示“半块”“小半块”“半块的半块”，进而教学分数各部分名称及分子、分母的含义。这样教学，让学生感受到数学和生活的紧密联系，将抽象的数学概念建立在熟悉的生活前概念之上。

在分数概念教学中，还要引导学生学会比较分子是1的两个分数的大小。由于受整数大小关系的影响，一开始，不少学生会错误地认为1/3大于1/2。这时，同样需要教师引导学生借助生活经验进行思考和分析。比如，可以将1/2理解为两个人平均分一块月饼，每人分得的那一份月饼的大小；可以将1/3理解为三个人平均分一块月饼，每人分得的那一份月饼的大小。这样，学生的生活经验“同样一块月饼，吃的人越多，每人吃到的就越少”被及时激活，进而学会分数大小的比较方法。

二、引导创造，让学生在动手实践中经历概念的形成过程

三年级上册要教学长度概念毫米，这一概念是学生在二年级学习了厘米概念的基础上进行学习的。厘米概念学习时，学生可以借助生活前概念进行学习。但毫米概念的建立，则需要借助已有的厘米概念。教学时，教师可以创设用厘米尺（教师需要给学生制作只有大格的尺子）测量数学课本的长、宽和厚的教学情境，引导学生动手测量，并记录长度。交流时，产生问题：“宽比18厘米长一些，又不到19厘米，厚1厘米都不到，怎么办？”然后引导学生独立思考、合作交流、动手实践，让每一位学生都经历将1厘米平均分成10份的过程，进而认识到其中的1小格是一个新的长度单位毫米。这样教学，不同于直接借助刻度尺告诉学生毫米概念的接受性学习方式，而是引导学生经历再创造的过程，在这一过程中，学生不仅掌握了数学概念，更重要的是渗透了数学思想方法，培养了动手实践的能力。

学习了毫米后，学生还要学习分米。教材直接告诉学生“10厘米是1分米”，再让学生“想一想，1米等于多少分米”。教学时，不能到此为止。教师可以借助课件演示用长度单位米测量物体的长度，发现结果不是整米数，于是将1米平均分成10份，让学生明白将1米平均分成10份，其中1份是一个新的长度单位分米。再用分米单位测量，结果也不是整分米数，于是将1分米再平均分成10份，产生新单位厘米。同样，继续量，继续分，产生毫米。让学生经历上述过程，有利于学生从整体上认识长度单位之间的十进制关系，使得学生的认知具有继续延伸拓展的张力，也为后续认识小数做好准備。

三、抓住本质，探索概念教学的最佳路径

三年级上册要学习“倍”的概念。这是学生在学习了乘法概念的基础上进行教学的，但“倍”不同于乘法，不是一种运算，而是表示两个数量之间的一种关系。分析教材，概念教学的路径是：胡萝卜有2根，红萝卜有“3个2根”——红萝卜的根数是胡萝卜的3倍；胡萝卜有2根，白萝卜有“5个2根”——白萝卜的根数是胡萝卜的5倍。从概念学习的角度分析，教材这样编写值得商榷。要教学“红萝卜的根数是胡萝卜的3倍”这个新的概念，只举一个例子，将“3个2根”表达为“3倍”，显然无法实现“列举有关概念的多个例证，并准确把握共同的本质属性”这一概念教学的基本要求。教材接着教学将“5个2根”表达为“5倍”，容易使学生产生错误的认知，将非本质属性“2根”误认为概念的本质属性。所以，教材编写的教学材料和教学路径并不是“倍”概念教学的最佳选择。

我们在教学设计时，创设了如下的探究活动：如图1，观察前两幅图中第二行圆圈个数和第一行圆圈个数的关系，把第三幅图中第二行的圆圈画出来。这是一个富有挑战性的学习任务，需要学生观察、思考，找到前两幅图中第二行数量与第一行数量之间的关系。在“倍”概念教学前，学生熟悉的是两个数量的“和”或者“差”的关系，因此学生解决这一问题时，有学生会想“第一幅图中，第二行比第一行多2个圈”“第二幅图中，第二行比第一行多4个圈”，因此“第三幅图中，第二行比第一行多6个圈”；还有学生只看第二行数量之间的变化规律，认为“第三幅图中，第二行有9个圈（比前一幅图的第二行多3个圈）”。当然，也会有学生从“倍”的角度来把握第二行和第一行数量之间的关系。

反馈交流时，教师引导学生先反馈从“比多少”的角度画的情况，再重点反馈从“倍”的角度画的情况，交流“为什么这样画”。并引导学生思考、交流：“这三幅图中蕴含了一个共同的秘密，你发现了吗？第二行圆圈个数是第一行的3倍，是怎样看出来的？”通过思考、交流，学生找到共同点：第一行都是“1份”，第二行都是同样的“3份”，这就是倍的本质属性。

接着，引导学生思考：“每个框里可以画几个？”让学生认识到1份的数量可以不同，但每1份的数量要同样多。教师可以继续追问：如果第二行拿掉一份，现在第二行的圆圈个数是第一行的几倍？增加一份呢？

上述教学，先通过列举概念的多个例证，使得学生准确把握了概念共同的本质属性，而且在观察、思考、创造的过程中，培养和发展了学生的推理能力、抽象概括能力。

四、多重体验，让概念理解更深刻

多重体验是小学生概念学习的重要特征和基本要求。由于中低年级学生抽象理解能力弱，概念学习（特别是几何概念的学习）需要充分借助直观，借助动手实践，通过多形式、多途径的体验，才能真正理解、掌握概念。

三年级上册要学习四边形这一几何概念，教材没有给出四边形的定义，而是要求借助丰富的活动，达成直观认识的目标。教学时，可以采用以下三个层次的数学活动。

1. 找一找：把你认为是四边形的图形圈出来。通过辨认，让学生初步认识四边形，知道四边形的特征：有四个角和四条直的边。

2. 画一画：在点子图上画出几个不同的四边形。通过动手操作，画出形状大小不同的多个四边形，从而去除非本质属性，建立四边形的概念。

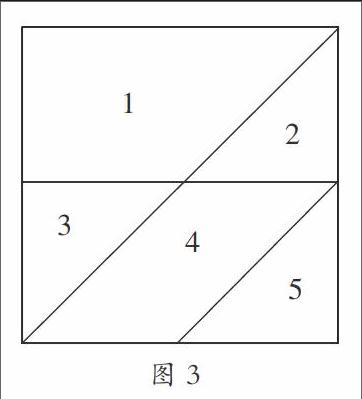
3. 数一数：图形中一共有几个四边形（图3）。这是一个富有挑战性的数学活动，学生要准确数出四边形的总个数，既需要依靠四边形概念的清晰程度，还需要依靠有序思考的方法。

通过以上多样化、有层次的数学活动，抽象的数学概念具体化、清晰化。同时在概念学习过程中，让学生的空间观念、数学能力得到充分发展。前面所述的分数概念、长度概念、关系概念（倍）的教学中，除了让学生充分经历概念的形成过程外，同样需要安排多重体验活动，以帮助学生及时内化概念，达成深刻理解。

（作者单位：浙江省嘉兴教育学院）