ECC/RC组合梁受弯性能试验研究与分析

乔 治 潘钻峰 梁坚凝 孟少平

(1东南大学土木工程学院, 南京 210096)(2同济大学土木工程学院, 上海 200092)(3香港科技大学土木工程学院,香港)

ECC/RC组合梁受弯性能试验研究与分析

乔 治1潘钻峰2梁坚凝3孟少平1

(1东南大学土木工程学院, 南京 210096)(2同济大学土木工程学院, 上海 200092)(3香港科技大学土木工程学院,香港)

工程用水泥基复合材料(ECC)具有超高的韧性与优异的裂缝控制能力,提出采用ECC制作U型永久性模板,与混凝土形成外包式ECC/RC组合梁,以提高构件的力学性能和耐久性能．给出了ECC/RC组合梁受弯非线性分析方法,并开展了3种不同界面处理方式的ECC/RC组合梁的弯曲性能试验研究．结果表明,相比RC梁,ECC/RC组合梁的承载力和延性均有所提高;当荷载低于极限承载力的80%时,组合梁的最大裂缝宽度小于100 μm;不同的界面处理对组合梁的极限承载力影响较小,但对延性系数有影响．试验结果验证了组合梁受弯非线性分析方法的正确性．基于ACI规范所采用的有效惯性矩法,提出了ECC/RC组合梁正常使用极限状态下挠度的简化计算方法,得到基于内力平衡的组合梁完全开裂截面的惯性矩公式,利用该简化方法计算得到的预测值与试验值吻合较好．

工程用水泥基复合材料;组合梁;界面处理;裂缝宽度;延性;挠度

混凝土材料存在抗拉强度低、韧性差、开裂后裂缝宽度难以控制等缺点,使得混凝土在桥梁、海港码头、大坝等处于恶劣环境结构中的应用面临严峻的耐久性问题．工程用水泥基复合材料(ECC)是一种具有高延性、高韧性和多缝开裂特征的纤维增强水泥基复合材料,纤维掺量在不大于2%的情况下,就可以达到2.0%以上的极限拉应变,拉伸过程中形成许多宽度小于100 μm的细裂缝,这种多缝开裂导致了该材料的拉伸应变硬化行为[1-2]．

基于ECC超高的拉伸韧性和优异的裂缝分散能力,将ECC材料替代混凝土应用于结构与构件中,将会使结构或构件在承载力和耐久性方面得到显著的改善[3-7]．为了进一步降低结构成本,更加合理地应用ECC材料,Maalej等[8]提出使用ECC替换受拉区钢筋两侧各一倍保护层厚度范围内的混凝土,对一根ECC/RC组合梁进行了初步探究．试验结果证明ECC可以有效地控制构件的裂缝宽度,提升组合梁的耐久性．随后许多学者对ECC/RC组合梁展开了很多研究．Xu等[9]开展了超高韧性复合材料控裂功能梯度复合梁的试验研究,结果表明采用 ECC替代受拉区混凝土可以显著提高梁的抗弯承载力和延性,复合梁在钢筋屈服前可使裂缝宽度保持在0.05 mm范围以内．Yuan等[10]对配有BFRP筋的ECC梁和ECC/RC组合梁进行了弯曲试验研究,表明ECC材料的应用可提高梁的承载力以及延性,有效减少梁中筋材用量．Leung等[11-12]采用ECC作为梁底模板,开展受弯试验,表明ECC是制作混凝土模板的理想选择之一．

目前所研究的ECC/RC组合梁中,ECC和混凝土大多是在同一时段先后浇筑的,后期一起硬化成型,界面黏结性能容易得到保证．而在实际结构应用中,ECC更适合在工厂预制成模板,一定龄期后运送到现场进一步浇筑混凝土．因此本文采用ECC制作U型永久性模板,模板成型14 d后与混凝土材料形成组合梁,提出了ECC/RC组合梁受弯非线性分析方法,设计了3种不同界面处理方式的ECC/RC组合梁,并开展受弯性能试验,研究ECC/RC组合梁在不同黏结性能下的破坏形态、裂缝开展、承载力及延性等力学性能．基于ACI规范所采用的有效惯性矩法,提出了ECC/RC组合梁正常使用极限状态下挠度的简化计算方法,并通过试验数据验证其合理性．

1 ECC/RC组合梁受弯性能非线性分析

1.1 受弯性能分析的基本假定

本文对ECC/RC组合梁受弯全过程分析时有如下基本假定:

1) 平截面假定.

2) 不考虑ECC与混凝土之间、水泥基材与钢筋之间的相对滑移．

1.2 材料本构关系

1.2.1 ECC的拉压本构模型

ECC材料在单轴受拉和单轴受压情况下的应力-应变曲线用图1给出的双线性模型来描述．ECC材料的拉应力σt-ECC和压应力σc-ECC分别表示为

(1)

(2)

式中，εt和εc分别为材料的拉应变和压应变；σtc和εtc为ECC的初裂应力和初裂应变；σtu和εtu为ECC的极限抗拉强度和极限拉应变；σcc和εcc为ECC的压缩弹性极限应力和对应的极限应变；σcu和εcu为ECC的峰值压应力和峰值压应变.

(a) 单轴拉伸应力-应变曲线

(b) 单轴压缩应力-应变曲线

Maalej等[13]建议σcc=2σcu/3且εcc=εcu/3．ECC材料的初裂应力σtc一般约为2～5 MPa,极限抗拉强力σtu通常为σtc的1.2～1.5倍．

为进一步降低ECC应用成本,可采用国产PVA纤维代替部分日产PVA纤维来配置混杂PVA-ECC[14],其配合比列于表1.通过四点弯曲和单轴压缩试验研究混杂PVA-ECC的基本力学性能,其中ECC的拉伸性能可根据四点弯曲试验结果推导得出[14-15],其单轴受拉和受压本构关系参数见表2．

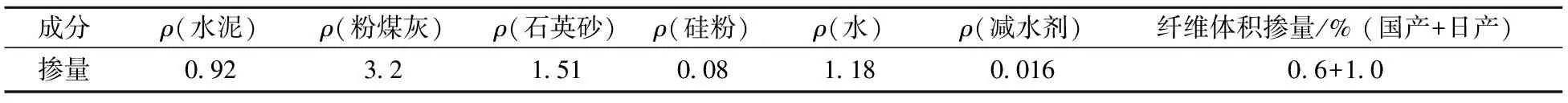
表1 PVA-ECC配合比 kg/m3

表2 ECC单轴拉压本构模型参数

1.2.2 混凝土拉压本构模型

为了简化计算,假定混凝土在单轴受拉状态下开裂后就退出工作,其单轴受压本构关系采用Hognestad模型[16],如图2所示,在任意时刻混凝土材料的拉应力σt-con和压应力σc-con分别表示为

(3)

(4)

式中,ft和εt0分别为混凝土的初裂应力和初裂应变；fc和ε0为混凝土的峰值压应力和峰值压应变；εu为混凝土的极限压应变.

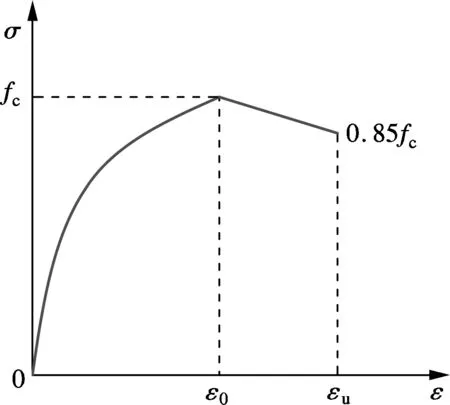
图2 混凝土受压应力-应变关系

1.2.3 钢筋的本构模型

钢筋的应力-应变曲线假定为理想弹塑性模型,其表达式如下:

(5)

式中,σs和εs分别为钢筋的应力和应变；Es为钢筋的弹性模量；fy为钢筋的屈服强度；εy为屈服应变；εs，h为极限拉伸应变.

1.3 非线性分析方法

根据上述各材料本构关系,可对ECC/RC组合梁进行受弯性能非线性分析,具体方法如下:假定截面受压边缘处的应变值为εcmax,将跨中截面沿高度方向分成n个条带,根据平截面假定可以得到第i条带混凝土、受拉钢筋和ECC的应变关系式．确定每个单元的应变后,根据假设的各种材料本构关系分别计算出各个单元的应力,结合截面的内力平衡方程,进行迭代求解出截面上各单元的应力值和应变值,进而计算出该截面的曲率和弯矩．逐级增加εcmax,并重复以上步骤,直至εcmax达到混凝土的极限压应变εu．文献[13-14]建议四点弯曲加载模式下梁跨中挠度可以用材料力学的方法近似计算,其公式为

(6)

式中,Δ为跨中挠度;φ为截面曲率;l为梁的计算跨度．采用条带法计算截面弯矩-跨中挠度关系时,需借助计算机编程软件进行反复迭代计算．本文采用Matlab软件编制相应的程序来计算ECC/RC组合梁的弯矩-跨中挠度曲线,并实时监测受拉区钢筋拉应变及εcmax的值,以提取出屈服荷载、屈服挠度、极限荷载、极限挠度等特征点．

2 试验概况

2.1 试验材料

本试验采用的水泥基材是强度等级为C40的普通混凝土和混杂PVA-ECC,ECC的配合比和材料力学性能见表1和表2．在浇筑混凝土时分别制作3个边长为100 mm的立方体试块和3个100 mm×100 mm×300 mm的棱柱体试块,与构件同条件养护,实测的混凝土轴心抗压强度fc为51.8 MPa,弹性模量Ec为41.9 GPa．试件所用钢筋的力学性能实测结果如表3所示．

表3 钢筋的力学性能

2.2 试验设计

本试验共设计了3组ECC/RC组合梁和1组RC对比梁,每组2个试件,梁截面尺寸均为120 mm×150 mm,ECC模板侧板厚度为20 mm,底板厚度为30 mm,如图3所示．试验梁长1.5 m,计算长度1.2 m,纵筋和箍筋均采用HRB400级钢筋,为使试件最终产生弯曲破坏,剪跨比设计为2.67,且在梁的剪跨区配置足够的箍筋,各试件详细参数见表4．试验梁的配筋形式与配筋量均相同,其中3组组合梁的不同之处在于ECC与混凝土的界面处理方式不同,分别为不处理、放置粗砂和横向凹槽,如图4所示．

表4 试验梁主要参数

图3 试验梁截面尺寸与配筋图(单位:mm)

图4 ECC/RC组合梁界面处理形式

2.3 试件浇筑

试件浇筑的过程分为2步: ① 浇筑U型ECC模板;② 在ECC模板内浇筑混凝土．制作U型ECC模板时,需对底板做3种内表面处理：① 不处理表面，只需抹平即可；② 粗砂处理表面，需在抹平后初凝前将平均直径为2 mm的粗砂均匀地铺在底板上并轻轻按压；③ 横向凹槽处理，将预先做好的钉有小木条的木板压在新浇的底板表面上,初凝后将木板移除,至此浇筑的第一步完成．底板养护14 d后,将U型模板内的浮灰清除干净,并将内表面用水打湿,将已绑扎好的钢筋笼放置在U型模板内,固定好位置,然后浇筑混凝土,并进行振捣密实．

2.4 试验加载方案与测点布置

试验装置及测点布置如图5所示．本试验在25 t液压伺服作动器上完成,试验加载开始时由荷载控制,加载至0.5 kN后持载100 s,然后继续加载,且加载由位移控制,速率为0.5 mm/min,当荷载下降至最大荷载的80%时停止试验．采用5个LVDT分别测量梁跨中、2个加载点与支座处的变形,在梁的纯弯段的每根受拉纵向钢筋上均粘贴2个钢筋应变片．在加载过程中时刻注意裂缝的开展情况,并使用150倍裂缝观测仪记录裂缝宽度的变化．

图5 试验装置及测点布置图(单位:mm)

3 试验结果分析

3.1 破坏模式

ECC/RC组合梁均发生了延性较好的弯曲破坏,多缝开裂的现象较为明显,在达到峰值荷载前,梁顶及梁两端面的ECC模板与混凝土界面处均未发现脱黏裂缝,即没有发生黏结破坏,这是由于采用U型ECC模板,增加了模板与混凝土的接触面积,界面即使未做处理,仍能保证足够的黏结承载力．由于试验梁中纵筋配筋率较高,使得RC对比梁的受弯承载力和受剪承载力较为接近,在剪跨区出现了较为明显的斜裂缝,破坏模式为弯剪破坏,而ECC/RC组合梁则未出现宽度较大的斜裂缝,表明ECC可有效提高梁的受剪承载力,减少箍筋用量．由于ECC优异的压缩韧性,受压区ECC在组合梁破坏时均未发生剥落现象．

3.2 荷载-跨中挠度曲线

8根试验梁的计算与实测的荷载-跨中挠度曲线如图6所示．由图可知,ECC/RC组合梁荷载-跨中挠度曲线的上升段与屈服后平稳段的计算值和实测值吻合较好,由于ECC材料没有考虑下降段,因此荷载位移曲线的下降段并没有预测．ECC/RC组合梁的荷载-跨中挠度曲线与RC梁较为类似,开裂前,试验梁均处于弹性状态,荷载与位移成线性关系;开裂后,梁的刚度有所下降,曲线呈现出非线性特性;梁屈服后经历一个曲线平缓段后发生破坏,表现出了良好的延性．尽管ECC的弹性模量较小(20.1 GPa),约为普通混凝土的1/2,但开裂后组合梁的刚度仅略小于RC梁,这是因为ECC开裂后仍然能够承担荷载,并能约束混凝土的裂缝开展,间接提高了组合梁的刚度．RC梁屈服后,荷载位移曲线较为平稳,而组合梁的屈服段呈现一定程度的软化趋势,这表明与ECC拉伸应变硬化特性相比,ECC与混凝土的脱黏在组合梁屈服后对承载力的影响更大些．组合梁的极限承载力均达到甚至超过了理论计算值,说明组合梁尽管屈服后发生了不同程度的脱黏,但并没有发生脱黏破坏,最终都是受压区混凝土压碎而导致的弯曲破坏．组合梁的下降段更为缓慢,这是由于ECC具有良好的压缩韧性,即使在很大的压应变下ECC仍然具有一定的残余强度．

图6 试验梁荷载-跨中挠度曲线

3.3 承载力与延性分析

实测的8根梁的特征荷载和特征位移如表5所示,Vy为屈服荷载,Δy为屈服跨中挠度,Vpeak为峰值荷载,Δpeak为峰值跨中挠度,Δu为试件所加荷载下降至峰值荷载的80%时对应的极限跨中挠度．本文采用位移延性系数μ来评价受弯梁的延性,即

μ= (7)

由表5可知,ECC/RC组合梁的屈服荷载和峰值荷载较RC梁分别提高了约14.0%和14.1%,这得益于ECC材料在开裂后的应变硬化特性．组合梁相较RC梁,承载力提高的幅度并不大,这是由于试验用混凝土的实际轴心抗压强度大于ECC;此外试验梁的纵筋率偏大,没有充分发挥ECC的开裂后抗拉强度．不同的界面处理对组合梁的承载力影响较小,但对延性系数影响较大．带有横向凹槽的组合梁表现出了最好的延性,而界面未处理的组合梁与RC梁的延性系数基本一致,说明ECC与混凝土之间良好的黏结可以有效地增加构件的延性．

3.4 裂缝分析

RC梁在纯弯段内出现首条弯曲裂缝,之后随着荷载的增加,新裂缝不断出现,梁屈服后,弯曲裂缝条数基本不变,而裂缝宽度快速增长,直至受压区混凝土压碎发生破坏．不同于RC梁,ECC/RC组合梁的弯曲裂缝发展贯穿于整个试验过程,即使在组合梁屈服后,裂缝条数仍继续增长,裂缝宽度增长缓慢,直到主裂缝出现为止．试验梁在破坏时的裂缝分布如图7所示．与RC梁相比,不同界面处理的ECC/RC组合梁均可将混凝土的单一裂缝逐渐扩散为多条细密裂缝,这主要是由于ECC开裂后并不退出工作,而是与钢筋一起继续承担拉力,ECC中PVA纤维的桥接作用形成了大量细密裂缝．

(a) N-1

(b) N-2

(c) S-1

(d) S-2

(e) T-1

(f) T-2

(g) RC-1

(h) RC-2

裂缝宽度随标准化荷载的变化规律见图8,图中标准化荷载为所加荷载与峰值荷载的比值．由图8可以看出,ECC/RC组合梁在达到各自峰值荷载的80%之前,裂缝宽度均小于100 μm．开裂混凝土的渗透性是裂缝宽度的三次幂[17],裂缝宽度小于100 μm时,可认为混凝土渗透性和未开裂混凝土基本一致[18]．一般而言,结构总是在正常使用状态下工作,正常使用状态的最大荷载一般为极限荷载的50%～70%．一般钢筋混凝土结构处于高腐蚀环境(三类环境)中,允许的最大裂缝宽度为0.2 mm[19]．由此可见,U型ECC模板可以有效地提高梁的耐久性．

图8 裂缝宽度与标准化荷载的关系曲线

4 正常使用极限状态下ECC/RC组合梁刚度计算方法

对于均匀弹性梁,弯曲刚度在各截面保持不变,可由虚功原理求出其挠度,但对于ECC/RC组合梁,正常使用状态下都是带裂缝工作的,裂缝的出现会导致截面弯曲刚度的减小.在四点弯曲加载模式下,ECC/RC组合梁的跨中挠度可根据弹性理论计算如下:

(8)

式中,Δpser为正常使用极限状态下的跨中挠度计算值;Ma为纯弯段截面弯矩;Ie为截面有效惯性矩,它可以根据 ACI规范[20]建议的下式计算得到:

(9)

式中,Ig为构件开裂前的毛截面惯性矩;Icr为构件完全开裂时的截面惯性矩;Mcr为截面弯曲开裂弯矩．

为了简化计算,这里采用2个假定:将ECC拉伸开裂后的硬化刚度取为0,忽略受拉区ECC对截面惯性矩的贡献;可将ECC/RC组合梁截面简化为一个ECC梁和RC梁,如图9所示．由于组合梁底部ECC层的厚度一般满足最小保护层厚度要求且能够包裹住钢筋即可,相比截面高度,ECC层厚度较小,简化的RC梁下部ECC层可被忽略．由此,组合梁的Ig和Icr可分别表示为

(10)

(11)

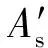
图9 简化的ECC/RC组合梁计算截面

组合梁截面弯曲开裂弯矩Mcr可按照弹性理论近似计算如下[20]:

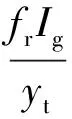
(12)

式中,yt为为受拉外边缘到截面中和轴的距离;fr为混凝土的弯拉强度,fr=0.62fc0.5．

受压区高度c可根据截面内力平衡求出．Ashour[21]进行的RC梁的弯曲试验表明,从开裂到纵筋屈服,截面中和轴高度基本保持不变,可将屈服时刻梁的惯性矩认为是完全开裂截面惯性矩．对于ECC/RC组合梁,完全开裂截面惯性矩Icr也可取为在梁屈服时刻的截面惯性矩．若进一步假定正常使用状态下,受压区ECC和混凝土的压应力均为线性分布,组合梁受压区高度c可通过以下方程获得:

εsyEsAs+b1(h-c)σtc

(13)

基于平截面假定,截面应变分布应该符合以下关系:

(14)

(15)

将式(14)和 (15)代入式(13),即可求出组合梁屈服时受压区高度c．

通过已进行的ECC/RC组合梁四点弯曲试验数据验证本文提出的弯曲变形简化计算方法．Rashid等[22]认为构件正常使用状态下最大荷载约为试验测得最大荷载的0.6倍．基于前文弯曲变形计算方法,即式(8)～(12),可计算得到正常使用极限荷载及屈服荷载时的挠度值,理论预测值与试验实测值均汇总于表6中．由表可知,相应的挠度计算值Δpser和Δpy均与实测值符合很好,Δpser/Δser的均值与变异系数为1.05 和0.12,而Δpy/Δy的均值与变异系数分别为1.04和0.14,与实测值基本一致．因此,基于本文所提出的基于内力平衡的中和轴高度以及完全开裂截面惯性矩Icr的理论计算方法,可以较好地预测ECC/RC组合梁正常使用极限状态下的挠度,从而为ECC/RC组合梁正常使用阶段的结构设计提供可靠依据．

表6 ECC/RC组合梁跨中挠度实测值与预测值

注：Vser为组合梁正常使用极限荷载的实测值;Δser为组合梁正常使用极限荷载下的挠度实测值;Δpy为组合梁屈服时刻挠度的预测值．

5 结论

1) 采用平截面假定和简化的材料本构关系,运用条分法,建立内力平衡方程,可计算得到ECC/RC组合梁的非线性受力过程,并与组合梁的试验结果进行了比较,验证了此方法的准确性．

2) ECC/RC组合梁均发生了延性较好的弯曲破坏,多缝开裂现象较为明显,在达到峰值荷载前均未发生黏结破坏,说明采用U型ECC模板可增大界面接触面积,有助于提高ECC与混凝土之间的黏结力．

3) ECC/RC组合梁的荷载-跨中挠度曲线与RC梁较为类似,但是组合梁在屈服后呈现出一定程度的软化现象,这表明与ECC的拉伸应变硬化特性相比,ECC与混凝土界面的脱黏效应在组合梁屈服后对承载力的影响更大．

4) ECC/RC组合梁在达到各自峰值荷载的80%之前,裂缝宽度均小于100 μm．结构在正常使用阶段的荷载一般为极限荷载的50%～70%,因此,U型ECC模板可以有效地提高梁的耐久性．

5) 本文提出了ECC/RC组合梁正常使用极限状态下挠度的简化计算方法,得到基于内力平衡的组合梁完全开裂截面的惯性矩公式,利用该简化方法计算得到的预测值与试验值吻合较好．

References)

[1]Li V C, Leung C K Y. Steady state and multiple cracking of short random fiber composites [J].JournalofEngineeringMechanics,ASCE, 1992, 188(11): 2246-2264. DOI:10.1061/(asce)0733-9399(1992)118:11(2246).

[2]Li V C, Stang H, Krenchel H. Micromechanics of crack bridging in fibre-reinforced concrete[J].MaterialsandStructures, 1993, 26(8): 486-494. DOI:10.1007/bf02472808.

[3]侯利军. 超高韧性水泥基复合材料弯曲性能及剪切性能试验研究 [D]. 大连: 大连理工大学土木工程学院, 2012.

[4]杨英姿, 祝瑜, 高小建, 等. 掺粉煤灰PVA纤维增强水泥基复合材料的试验研究[J]. 青岛理工大学学报,2009, 30(4): 51-54,59. DOI:10.3969/j.issn.1673-4602.2009.04.011. Yang Yingzi, Zhu Yu, Gao Xiaojian, et al. Experimental study on high-ductile PVA fiber-reinforced cement-based composite materials with fly ash[J].JournalofQingdaoTechnologicalUniversity, 2009, 30(4): 51-54,59. DOI:10.3969/j.issn.1673-4602.2009.04.011.(in Chinese)

[5]李庆华, 徐世烺. 钢筋增强超高韧性水泥基复合材料受弯构件理论分析[J]. 工程力学, 2010, 27(7):92-102. Li Qinghua, Xu Shilang. Theoretical analysis on flexural behavior of reinforced ultra high toughness cementitious composite members [J].EngineeringMechanics, 2010, 27(7): 92-102. (in Chinese)

[6]薛会青, 邓宗才. HRECC梁弯曲性能的试验研究与理论分析[J]. 土木工程学报, 2013, 46(4): 10-17. Xue Huiqing, Deng Zongcai. Experimental and theoretical studies on bending performance of HRECC beams [J].ChinaCivilEngineeringJournal, 2013, 46(4): 10-17. (in Chinese)

[7]Fischer G, Li V C. Effect of matrix ductility on the performance of reinforced ECC column members under reversed cyclic loading conditions [C]//ProceedingsoftheJCIInternationalWorkshoponDuctileFiberReinforcedCementitiousComposites(DFRCC). Takayama, Japan, 2002: 269-278.

[8]Maalej M, Li V C. Introduction of strain-hardening engineered cementitious composites in design of reinforced concrete flexural members for improved durability [J].ACIStructuralJournal, 1995, 92(2): 167-176.

[9]Xu Shilang, Li Qinghua. Theoretical analysis on bending behavior of functionally graded composite beam crack-controlled by ultrahigh toughness cementitious composites[J].ScienceinChinaSeriesE:TechnologicalSciences, 2009, 52(2):363-378. DOI:10.1007/s11431-008-0337-9.

[10]Yuan F, Pan J, Leung C K Y. Flexural behaviors of ECC and concrete/ECC composite beams reinforced with basalt fiber-reinforced polymer [J].JournalofCompositesforConstruction, 2013, 17(5): 591-602. DOI:10.1061/(asce)cc.1943-5614.0000381.

[11]Leung C K Y, Cao Q. Development of pseudo-ductile permanent formwork for durable concrete structures[J].MaterialsandStructures, 2009, 43(7): 993-1007. DOI:10.1617/s11527-009-9561-4.

[12]Li H, Leung C K Y, Xu S, et al. Potential use of strain hardening ECC in permanent formwork with small scale flexural beams[J].JournalofWuhanUniversityofTechnology(MaterialsScienceEdition), 2009, 24(3): 482-487. DOI:10.1007/s11595-009-3482-5.

[13]Maalej M, Li V C. Flexural/tensile-strength ratio in engineered cementitious composites[J].JournalofMaterialsinCivilEngineering, 1994, 6(4): 513-528. DOI:10.1061/(asce)0899-1561(1994)6:4(513).

[14]乔治, 潘钻峰, 孟少平, 等. 混杂 PVA-ECC 配合比优化设计及力学性能试验研究[J]. 土木建筑与环境工程, 2015, 37(5): 72-81. DOI:10.11835/j.issn.1674-4764.2015.05.011. Qiao Zhi, Pan Zuanfeng, Meng Shaoping, et al. Optimization of mix proportion and experimental analysis of mechanical properties of hybrid PVA-ECC[J].JournalofCivil,ArchitecturalandEnvironmentalEngineering, 2015, 37(5): 72-81. DOI:10.11835/j.issn.1674-4764.2015.05.011.(in Chinese)

[15]蔡向荣, 徐世烺. UHTCC薄板弯曲荷载-变形硬化曲线与单轴拉伸应力-应变硬化曲线对应关系研究[J]. 工程力学, 2010, 27(1): 8-16. Cai Xiangrong, Xu Shilang. Study on corresponding relationships between flexural load-deformation hardening curves and tensile stress-strain hardening curves of UHTCC[J].EngineeringMechanics, 2010, 27(1): 8-16. (in Chinese)

[16]Hognestad E, McHenry D, Hanson N W. Concrete stress distribution in ultimate strength design [J].JournaloftheAmericanConcreteInstitute, 1955, 27(4): 455-479.

[17]Tsukamoto M. Tightness of fiber concrete [J].DarmstadtConcrete, 1990, 5: 215-225.

[18]Wang K, Jansen D C, Shah S P, et al. Permeability study of cracked concrete[J].CementandConcreteResearch, 1997, 27(3): 381-393. DOI:10.1016/s0008-8846(97)00031-8.

[19]中华人民共和国住房和城乡建设部. GB 50010—2010. 混凝土结构设计规范[S]. 北京:中国建筑工业出版社, 2010.

[20]American Concrete Institute. ACI 318-14 Building code requirements for structural concrete [S]. Detroit: American Concrete Institute,2014.

[21]Ashour S A. Effect of compressive strength and tensile reinforcement ratio on flexural behavior of high-strength concrete beams[J].EngineeringStructures, 2000, 22(5): 413-423. DOI:10.1016/s0141-0296(98)00135-7.

[22]Rashid M A, Mansur M A. Reinforced high-strength concrete beams in flexure [J].ACIStructuralJournal, 2005, 102(3): 462-471.

Experimental study and analysis of flexural behavior >of ECC/RC composite beams

Qiao Zhi1Pan Zuanfeng2Leung C K Y3Meng Shaoping1

(1Shool of Civil Engineering, Southeast University, Nanjing 210096, China) (2School of Civil Engineering, Tongji University, Shanghai 200092, China) (3School of Civil Engineering, Hong Kong University of Science and Technology, Hong Kong, China)

Engineered cementitious composite (ECC) has ultra-high toughness and excellent crack controlling ability. A type of ECC/RC(reinforced concrete) composite beam constructed with the U-shape permanent formwork made by ECC is proposed, in order to improve the durability and mechanical performance. A full-range nonlinear analysis method for flexural behavior of ECC/RC composite beam is presented, and three interface treatments of composite beam are designed to study the flexural behavior. Results indicate that, compared with RC beam, both the load bearing capacity and ductility of composite beam are increased. Furthermore, the crack width of composite beam is less than 100 μm when the applied load is lower than 80% of the peak load. The interface treatments in ECC/RC composite beams have little effect on the flexural strength, but they affect the member ductility to a certain extent. The calculated load-displacement curves by the proposed method are shown to be consistent with the test data. Based on the method of effective moment of inertia suggested by ACI code, a simplified calculation method of deflection for ECC/RC composite beam at the serviceability limit state is proposed, and the equations for the inertia moment of the full cracked section based on the internal force equilibrium are also obtained. The predicted deflection based on the proposed simplified calculation method shows good consistence with the experimental results.

engineered cementitious composite (ECC); composite beam; surface treatment; crack width; ductility; deflection

10.3969/j.issn.1001-0505.2017.04.016

2016-12-15. 作者简介: 乔治(1989—),男,博士生;潘钻峰(联系人),男,博士,助理教授,zfpan@tongji.edu.cn.

国家自然科学基金青年基金资助项目(51208093)、国家自然科学基金委员会-国际交流资助项目(5141101015)、教育部博士点基金资助项目(20120092120021).

乔治,潘钻峰,梁坚凝,等.ECC/RC组合梁受弯性能试验研究与分析[J].东南大学学报(自然科学版),2017,47(4):724-731.

10.3969/j.issn.1001-0505.2017.04.016.

TU375.1, TU528.58

A

1001-0505(2017)04-0724-08