基于支持向量机的加密流量识别方法

程 光 陈玉祥

(东南大学计算机科学与工程学院, 南京 211189)(东南大学教育部计算机网络与信息集成重点实验室, 南京 211189)

基于支持向量机的加密流量识别方法

程 光 陈玉祥

(东南大学计算机科学与工程学院, 南京 211189)(东南大学教育部计算机网络与信息集成重点实验室, 南京 211189)

针对现有的加密流量识别方法难以区分加密流量和非加密压缩文件流量的问题,对互联网中的加密流量、txt流量、doc流量、jpg流量和压缩文件流量进行分析,发现基于信息熵的方法能够有效地将低熵值数据流和高熵值数据流区分开.但该方法不能识别每个字节是随机的而全部流量是伪随机的非加密压缩文件流量,因此采用相对熵特征向量{h0,h1,h2,h3}区分低熵值数据流和高熵值数据流,采用蒙特卡洛仿真方法估计π值的误差perror来区分局部随机流量和整体随机流量.最终提出基于支持向量机的加密流量和非加密流量的识别方法SVM-ID,并将特征子空间φSVM={h0,h1,h2,h3,perror}作为SVM-ID方法的输入.将SVM-ID方法和相对熵方法进行对比实验,结果表明,所提方法不仅能够很好地识别加密流量,还能区分加密流量和非加密的压缩文件流量.

加密流量识别;相对熵;蒙特卡洛仿真;支持向量机

近年来,随着网络技术的高速发展,网络安全问题也得到了人们越来越多的关注.一些恶意软件通过加密通道技术绕过防火墙和入侵识别系统[1]将机密信息发送到外网,如僵尸网络[2]、木马和高级持续性威胁(APT)[3].APT攻击普遍采用未知木马进行远程控制,通过隐蔽通道、加密通道避免网络行为被检测,同时攻击持续数月甚至数年时间.因此有效识别和检测加密流量对维护网络安全运行有着重要意义.

文献[4-5]综述了网络加密流量的识别研究现状,并从多个角度进行分析对比,认为加密和非加密流量的分类是现在一个重要的研究方向.当前加密流量识别方法有4类:基于负载随机性检测的方法、基于有效负载的识别方法、基于机器学习的方法、多种策略相结合的混合方法.赵博等[6]提出一种基于加权累积和检验的加密流量盲识别方法,该方法通过对待检测数据流中的网络报文负载依次进行累积和检验,然后参考实际报文长度对所得结果进行加权总和,实现加密流量的识别.Bonfiglio等[7]提出一种通过2个互补方法来识别Skype流量的框架,确定具体的协议数据流.Okada等[8]通过计算未加密流量与加密流量的相关性从49种特征中选取29种未加密流量与加密流量强相关的特征,根据相关性特征采用机器学习方法识别加密与未加密混合流量.Dorfinger等[9]通过第1个数据包的有效载荷的熵估计进行识别.Sun等[10]采用特征匹配方法识别SSL/TLS流量,然后应用统计分析方法确定具体的应用协议.Callado等[11]通过4种不同的组合机制在4个不同的网络场景下进行验证.Alshammari等[12]使用多种监督学习分类方法来识别SSH和非SSH,以及Skype和非Skype.以上方法基本没有考虑非加密压缩文件流量的处理,导致压缩文件流量被误识别为加密流量.互联网中压缩文件流量在流量成分中所占的比重较大,压缩文件流量的误报将大大影响算法的性能.

针对以上问题,本文通过对互联网中的加密流量、txt流量、doc流量、jpg流量、压缩文件流量这5种流量进行分析,发现基于信息熵方法不能识别非加密压缩文件流量.通过分析文件压缩原理发现,局部字符的出现规律会具有一定的随机性,但是文件在压缩前字符出现的概率仍符合一定的统计规律,从而使得压缩后从整体上来看体现出的是一种伪随机性,并不会像加密流量那样表现出高的随机性.由此本文提出将蒙特卡洛仿真方法估计π值的误差和相对熵作为流量分类测度,采用基于支持向量机(SVM)的分类方法(SVM-ID)对加密流量和非加密的压缩文件流量进行分类.将SVM-ID方法和相对熵方法进行对比实验,结果表明,本文方法不仅能够很好地识别加密流量,还能很好地区分加密流量和非加密的压缩文件流量.

1 基于支持向量机的加密流量识别方法

1.1 流量随机性分析

熵理论目前被广泛应用于信息安全领域的数据分析和异常检测.熵可用来表示能量分布均匀程度,能量分布越均匀,熵就越大.熵计算有香农熵和Tsallis熵2种方法[13].

本文选择doc流量、txt流量、jpg流量、压缩文件流量、加密流量这5种文件流量,采用香农熵的方法以8 bit作为一个码元符号逐字节计算字符熵,图1是5种文件类型字符熵值图.从图1可知,doc和txt文件熵值略小,jpg、压缩文件、加密流量负载熵值均接近8,本质上jpg图像文件也是一种压缩文件.因此基于信息熵的方法能够有效地将低熵值数据流和高熵值数据流区分开.但是,仅使用该方法并不能很好地区分压缩文件和加密流量.

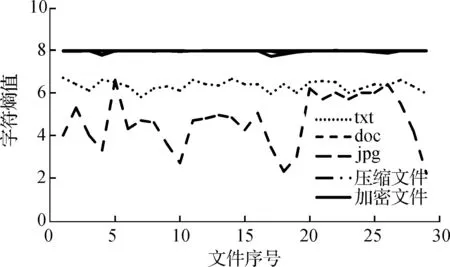
图1 5种文件类型字符熵值图

1.2 相对熵

本文使用相对熵作为特征向量.针对流量文件F,文件中的每一个字节都可以当作集合S中的一个元素Si,这样便可以得到文件中所有字节的熵.更一般地,可以将文件F中任意的K个连续字节当作一个元素,并计算给定文件中所有K个连续字节所组成的新集合S′的熵值.下面定义fk代表所有的K个连续字节所组成的集合,hk为该集合所对应的相对熵,其计算公式为

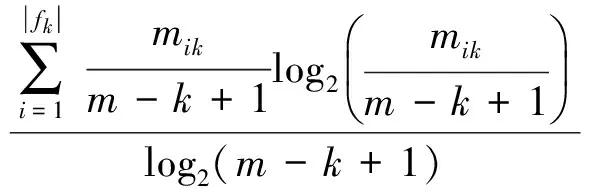
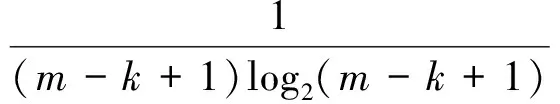
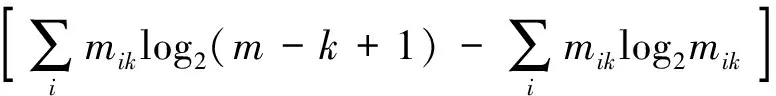
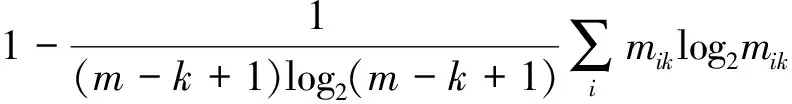
(1)

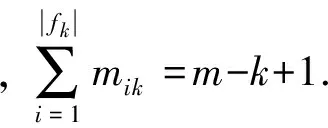
如前所述,对一个特定的文件,相应的特征有h1,h2,…,hn,但在实际应用中,可能存在不相关的特征,特征之间也可能存在相互依赖.此外,考虑到实时加密流量识别应用场景的需要,需要进行特征选择,剔除冗余特征,在保证所构建出来的分类器具有比较好的识别效果的同时,减少运行时间,提高系统识别效率.本文采用徐峻岭等[14]提出的特征选择算法选择{h0,h1,h2,h3}.Burges等[15]和Wang等[13]都只使用数据流的前几个数据包进行加密流量的识别,本文采用文献[16]的实验结果,计算有效负载前1 KB内容的相对熵{h0,h1,h2,h3}.由于加密通信信道的性质,在实际流量中,加密流的有效负载都大于1 KB.

1.3 蒙特卡洛π值估计误差

数据压缩的原理是找出那些重复出现的字符串,然后用更短的符号代替,从而达到缩短字符串的目的,所以压缩后的文件中字符偏向于均匀分布,从而熵值较大,这与数据加密类似.本文将采用蒙特卡洛π估计误差对全局随机性进行评估.蒙特卡洛方法的基本思想是通过实验的方法求解问题的概率,蒙特卡洛π值估计法的过程是：在一个正方形内有一个内切圆,向这个正方形内随机画点,点落入圆内的概率p为圆面积与正方形面积之比,π=4p,越均匀分布的数据点集所得到的π估计值越接近其真实值,从而可以根据蒙特卡洛π估计误差来表征数据集的随机性.由此本文给出了针对网络流量字节的蒙特卡洛π估计误差算法,算法的基本思路如下:对于每个需要处理的数据文件,每48 bit比特流作为一组计算一个蒙特卡洛仿真点,前24 bit作为montex,后24 bit作为montey,利用montex和montey计算48 bit比特流的点是否落在圆面积内,根据落在圆面积中的点数估计出蒙特卡洛π值,然后计算蒙特卡洛π值和真实π值之间的差.

图2为加密文件、jpg文件和压缩文件的蒙特卡洛π估计误差的统计结果.由图2可知,压缩文件和jpg文件的蒙特卡洛π估计误差较大,而加密文件的则比较小,因此基于蒙特卡洛 π估计误差值能够将加密流量、jpg以及压缩文件流量区分开.

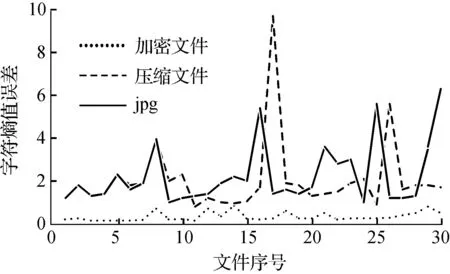
图2 3种文件的蒙特卡洛π估计误差

加密流量分类器所采用的特征子空间设置为φSVM={h0,h1,h2,h3,perror},其中perror为蒙特卡洛仿真方法估计π值的误差值.

1.4 基于支持向量机加密流量识别方法架构

支持向量机(SVM)是一种输入特征空间上间隔最大的线性分类器,本文使用SVM将待检测流量分为加密流量和非加密流量.加密流量识别是一个二类分类问题,数据的特征空间{h0,h1,h2,h3,perror}是一个4维空间,这里用x表示,类别加密和非加密用y表示,加密取1,非加密取-1,因此本文的分类目标是在所确定的4维空间中找到一个分类的超平面.SVM-ID方法流程如图3所示.

图3 SVM-ID方法流程图

SVM-ID方法主要包括2个过程:支持向量机的分类器训练过程和加密流量分类过程.训练过程主要由训练样本获取和分类器训练2个功能模块构成,其中分类器训练模块采用有标记的训练数据的特征值{h0,h1,h2,h3,perror}作为输入,使用LibSVM的SVM分类器进行模型的训练.在得到分类器后,模型一直存在检测系统中,随时供决策判断模块调用.

分类过程主要有数据采集、会话生成、会话过滤、相对熵计算、误差计算、决策判断、结果输出等功能模块.其中会话过滤模块对数据流根据相应规则完成过滤.相对熵计算模块使用文件数据有效负载的前1 KB内容根据式(1)计算相对字符熵h0,h1,h2,h3.误差计算模块采用文件数据的有效负载计算其蒙特卡洛π值的误差.决策判断模块对未知网络通信流量进行分析,使用分类器训练阶段产生的分类模型对未知流量进行判断,并对分类结果进行决策评估.

1.5 时间复杂度分析

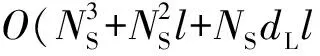
加密流量分类过程主要由相对熵计算、蒙特卡洛π值误差估计和决策判断3个过程构成.设相对熵的文件长度为A,K为连续字节数,n为需要计算相对熵的数量,则相对熵计算的时间复杂度为O(nAK).计算蒙特卡洛π值估计误差的时间复杂度为O(A),决策判断过程的时间复杂度为O(1),因此整个算法的时间复杂度为O(nAK).

2 实验分析

SVM-ID算法采用C语言进行编写,第三方软件及API包括:libpcap,pthread,LibSVM.主机的配置为:HP ProLiant BL465c服务器,CPU为双核皓龙2216 HE 2.4 GHz,内存8 GB,硬盘1 TB;操作系统为Red Hat 3.4.6-2.本文将SVM-ID算法和常用的只采用相对熵的相对熵方法进行对比实验.

2.1 数据集

实验数据集的获取过程为:使用4台普通主机(拓扑结构如图4所示)向FTP服务器以加密方式传送数据来获得加密流量,通过嗅探捕获在数据传输过程中产生的数据包.另外还捕获主机在正常通信时的数据样本流量.最后将这这些数据样本使用Wireshark的mergecap命令将其整合成一个pcap文件,形成最终数据集.

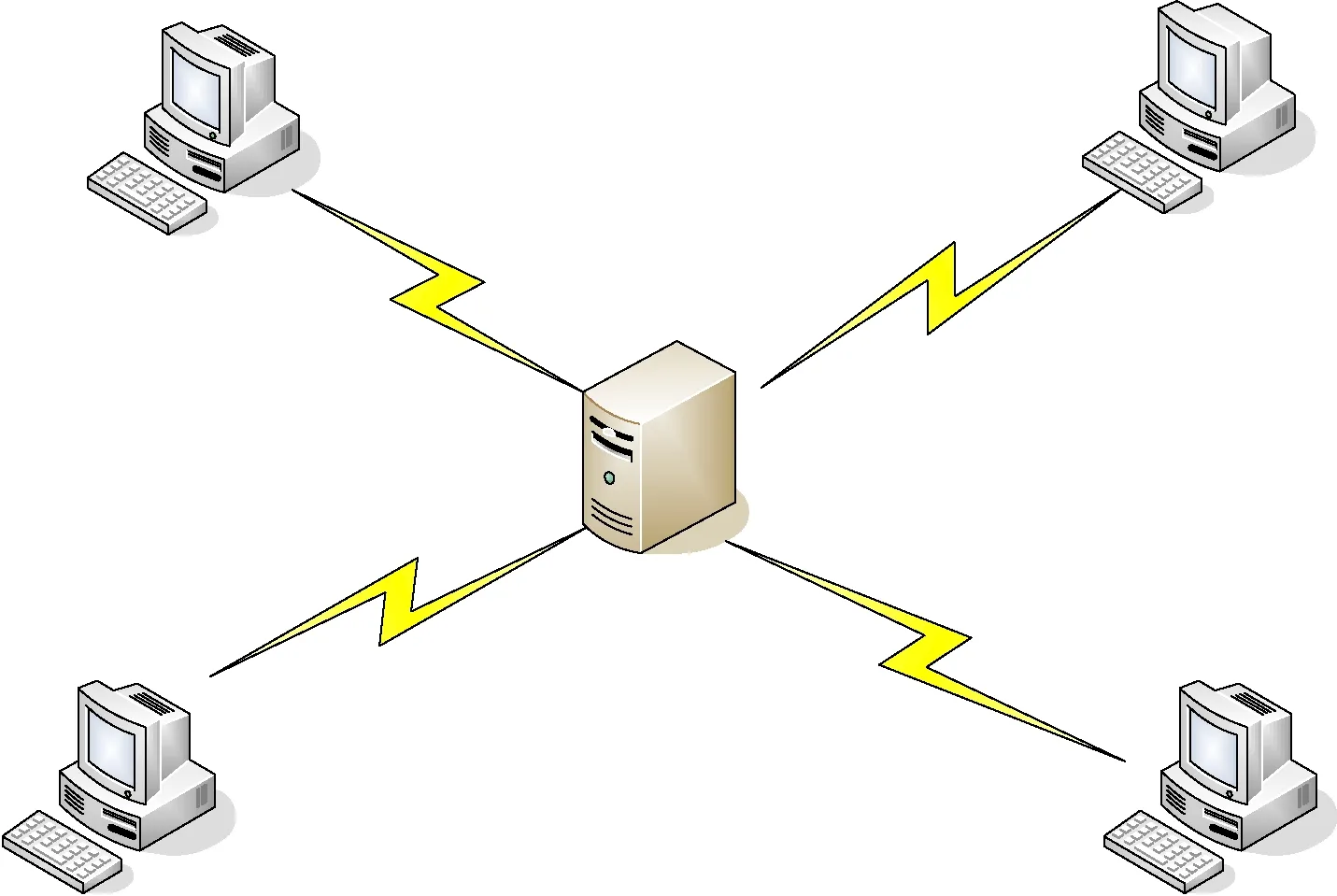
图4 数据采集网络拓扑结构

在传统的监督学习中,分类器通过对大量有标记的训练实例进行学习,从而建立模型用于预测未标记实例的类别.收集大量未标记实例是相当容易的,而获取大量有标记的实例则相对较为困难.这里,为了简化训练分类器的过程,训练样本的特征是通过对已标记的加密流量和非加密流量进行特征提取得到的,从而可以用来方便地对SVM分类器进行快速训练.

2.2 算法结果分析

为了评价识别算法的性能,本文选用查准率、查全率和综合评价3种评价指标.查准率Pr、查全率Re和综合评价Fm的计算公式为

Pr=TP/(TP+FP)

(2)

Re=TP/(TP+FN)

(3)

Fm=2PrRe/(Pr+Re)

(4)

式中,TP为加密样本中被正确标记的样本数;FN为加密样本中被误标识为非加密的样本数;FP为非加密样本中被误标识为加密的样本数.

查准率和查全率体现了识别方法的识别效果,Fm是根据查准率Pr和查全率Re二者给出的一个综合的评价指标,当Fm较高时则说明该方法比较理想.

本文先选取50个加密通信流和100个正常数据流组成训练样本对SVM模型进行训练,构建SVM分类器.然后选取73个加密通信流和276个正常数据通信流,使用加密流量识别方法对这些会话数据流进行检测.分别采用本文的SVM-ID方法和不采用蒙特卡洛π估计误差值的相对熵方法进行实验,结果如表1所示.

由表1可知,SVM-ID方法的查准率、查全率和综合评价分别为94.03%,91.31%,92.65%.不采用蒙特卡洛π估计误差的相对熵方法的查准率、查全率和综合评价分别为58.82%,86.96%,70.18%.可看出，本文SVM-ID方法的识别效果要优于相对熵方法.这是由于相对熵方法单纯采用相对熵,会将压缩文件类流量误判为加密流量,因此在正常流量中会存在一定的误报,由表1可知,42个正常的通信流被识别为加密流量从而提高了误报率,而对加密通信流的识别这2种方法的结果偏差不是很大.

表1 2种分类算法针对加密和正常流量结果对比

对所有加密流中识别出来的和未识别出来的流进行包数和字节数的统计,发现未被识别出的加密流量都是报文数和字节数都比较小的短流,而被识别出的是报文数和字节数都较大的长流,说明本文识别算法对通信数据量较小的加密流量识别效果不佳.其原因是混乱性和随机性是一种从统计学角度进行度量的特征,如果样本数据量少,可能不能从这2个特征尺度对其进行考量.

3 结论

1) 对互联网中的加密流量、txt流量、doc流量、jpg流量、压缩文件流量5种流量进行了分析,发现基于信息熵的方法能够有效地将低熵值数据流和高熵值数据流区分开,但是不能区分非加密压缩文件和加密文件.

2) 考虑到相对熵具有很好的局部随机性的识别能力,且支持向量机在二类分类上具有很好的分类特性,提出将蒙特卡洛仿真方法估计π值的误差和相对熵作为流量分类测度,利用支持向量机算法对加密流量和非加密的压缩文件流量进行分类.

3) 将本文提出的SVM-ID方法和相对熵方法进行对比实验,结果表明本文方法准确率较高且实时性好,优于仅使用相对熵特征向量的方法.

References)

[1]Fadlullah Z M, Taleb T, Vasilakos A V, et al. DTRAB: Combating against attacks on encrypted protocols through traffic-feature analysis[J].IEEE/ACMTransactionsonNetworking, 2010, 18(4): 1234-1247. DOI:10.1109/tnet.2009.2039492.

[2]Gu G, Perdisci R, Zhang J, et al. BotMiner: Clustering analysis of network traffic for protocol- and structure-independent botnet detection[C]//USENIXSecuritySymposium. San Jose, CA, USA, 2008: 139-154.

[3]Tankard C. Advanced persistent threats and how to monitor and deter them[J].NetworkSecurity, 2011, 2011(8): 16-19. DOI:10.1016/s1353-4858(11)70086-1.

[4]潘吴斌,程光,郭晓军,等.网络加密流量识别研究综述及展望[J].通信学报,2016,37(9):154-167. DOI:10.11959/j.issn.1000-436x.2016187. Pan Wubin, Cheng Guang, Guo Xiaojun, et al. Review and perspective on encrypted traffic identification research[J].JournalonCommunications, 2016, 37(9): 154-167. DOI:10.11959/j.issn.1000-436x.2016187.(in Chinese)

[5]Cao Z, Xiong G, Zhao Y, et al. A survey on encrypted traffic classification[C]//InternationalConferenceonApplicationsandTechniquesinInformationSecurity. Berlin: Springer, 2014, 490: 73-81. DOI:10.1007/978-3-662-45670-5_8.

[6]赵博,郭虹,刘勤让,等.基于加权累积和检验的加密流量盲识别算法[J].软件学报,2013,24(6):1334-1345. Zhao Bo, Guo Hong, Liu Qinrang, et al. Protocol independent identification of encrypted traffic based on weighted cumulative sum test[J].JournalofSoftware, 2013, 24(6): 1334-1345.(in Chinese)

[7]Bonfiglio D, Mellia M, Meo M, et al. Revealing skype traffic: When randomness plays with you[J].ACMSIGCOMMComputerCommunicationReview, 2007, 37(4): 37-48. DOI:10.1145/1282427.1282386.

[8]Okada Y, Ata S, Nakamura N, et al. Comparisons of machine learning algorithms for application identification of encrypted traffic[C]//10thIEEEInternationalConferenceonMachineLearningandApplicationsandWorkshops. Honolulu, USA, 2011, 2: 358-361. DOI:10.1109/icmla.2011.162.

[9]Dorfinger P, Panholzer G, John W. Entropy estimation for real-time encrypted traffic identification (short paper)[C]//InternationalWorkshoponTrafficMonitoringandAnalysis. Vienna, Austria, 2011: 164-171. DOI:10.1007/978-3-642-20305-3_14.

[10]Sun G L, Xue Y, Dong Y, et al. A novel hybrid method for effectively classifying encrypted traffic[C]//2010IEEEGlobalTelecommunicationsConference. Miami, USA, 2010: 1-5. DOI:10.1109/glocom.2010.5683649.

[11]Callado A, Kelner J, Sadok D, et al. Better network traffic identification through the independent combination of techniques[J].JournalofNetworkandComputerApplications, 2010, 33(4): 433-446. DOI:10.1016/j.jnca.2010.02.002.

[12]Alshammari R, Zincir-Heywood A N. Can encrypted traffic be identified without port numbers, IP addresses and payload inspection?[J].ComputerNetworks, 2011, 55(6): 1326-1350. DOI:10.1016/j.comnet.2010.12.002.

[13]Wang Y, Zhang Z, Guo L, et al. Using entropy to classify traffic more deeply[C]//2011IEEESixthInternationalConferenceonNetworking,Architecture,andStorage. Dalian, China, 2011. DOI:10.1109/nas.2011.18.

[14]徐峻岭,周毓明,陈林,等.基于互信息的无监督特征选择[J].计算机研究与发展,2012,49(2):372-382. Xu Junling, Zhou Yuming, Chen Lin, et al. An unsupervised feature selection approach based on mutual information[J].JournalofComputerResearchandDevelopment, 2012, 49(2): 372-382.(in Chinese)

[15]Burges C J C. A tutorial on support vector machines for pattern recognition[J].DataMiningandKnowledgeDiscovery, 1998, 2(2): 121-167.

[16]Bernaille L, Teixeira R. Early recognition of encrypted applications[C]//InternationalConferenceonPassiveandActiveNetworkMeasurement. Louvain-la-neuve, Belgium, 2007: 165-175.

Identification method of encrypted traffic based on support vector machine

Cheng Guang Chen Yuxiang

(School of Computer Science and Engineering, Southeast University, Nanjing 211189, China)(Key Laboratory of Computer Network and Information Integration of Ministry of Education, Southeast University, Nanjing 211189, China)

The existing methods of encrypted traffic classification are difficult to effectively distinguish encrypted traffic and compressed file traffic. Through analyzing the encrypted traffic, txt traffic, doc traffic, jpg traffic,and compressed file traffic, it is found that the methods based on information entropy can effectively separate the low entropy traffic and the high entropy traffic. However, this method cannot distinguish non-encrypted compressed file traffic with byte randomness and full flow pseudo randomness. Therefore, the relative entropy feature vector {h0,h1,h2,h3} is employed to distinguish the low entropy traffic and the high entropy traffic,and the Monte Carlo simulation method is used to estimate the error of π value,perror, which can be used to distinguish the local random traffic and the whole random traffic. Finally, a support vector machine (SVM)-based identification method (SVM-ID) for encrypted traffic and non encrypted traffic is proposed. And, the SVM-ID method uses the feature spaceφSVM={h0,h1,h2,h3,perror} as the input. The SVM-ID method is compared with the relative entropy method. The experimental results show that the proposed method can not only identify the encrypted traffic well, but also distinguish the encrypted traffic and the non-encrypted compressed file traffic.

encrypted traffic identification; relative entropy; Monte Carlo simulation; support vector machine

10.3969/j.issn.1001-0505.2017.04.005

2016-12-04. 作者简介: 程光(1973—),男,博士,教授,博士生导师, gcheng@njnet.edu.cn.

国家高技术研究发展计划(863计划)资助项目(2015AA015603)、国家自然科学基金资助项目(61602114)、中兴通讯研究基金资助项目、软件新技术与产业化协同创新中心资助项目.

程光,陈玉祥.基于支持向量机的加密流量识别方法[J].东南大学学报(自然科学版),2017,47(4):655-659.

10.3969/j.issn.1001-0505.2017.04.005.

TP393.4

A

1001-0505(2017)04-0655-05