5自由度主动磁悬浮轴承的积分滑模变结构控制

侯勇，王磊

（天津科技大学 电子信息与自动化学院，天津 300222）

主动磁悬浮轴承（Active Magnetic Bearings，AMB）系统是一个多输入多输出、非线性强、耦合程度高的复杂系统，其运行的可靠性和稳定性在很大程度上取决于系统的控制方法，采用常规的PID控制理论不能很好地满足系统对稳定性和动态特性的要求［1-4］。采用PID与其他控制策略的结合，虽然精度高，但控制系统设计复杂。滑模变结构控制具有对内部参数和外部扰动不敏感、鲁棒性好等优点，将其应用于主动磁悬浮轴承系统的控制，可以有效提高系统的运行性能。文献［5］针对主动磁悬浮轴承系统采用了滑模变结构控制，属于单自由度的分散控制，将其应用于多输入多输出系统时，依然存在静态误差大等问题。文献［6］应用积分滑模变结构控制实现了径向4自由度主动磁悬浮轴承的控制，但没有考虑轴向的控制，如进行包含轴向自由度的5自由度控制时，则需2套独立的控制系统，增加了控制器的数量，使实际应用更为复杂，而且忽略了传感器安装位置导致的耦合问题，会使系统达到稳态的时间增长。

分析5自由度主动磁悬浮轴承系统因传感器位置产生的耦合问题，推导并建立输出解耦的主动磁悬浮轴承状态方程，在此基础上研究多输入多输出积分滑模变结构控制方法，采用一套控制器实现了系统的5自由度控制。

1 5自由度主动磁悬浮轴承状态方程

主动磁悬浮轴承的转子共有6个自由度：3个平动自由度和3个转动自由度，其中转子绕轴向转动的自由度不受轴承控制器控制，而其余的5个自由度则需磁悬浮轴承控制器控制。5自由度磁悬浮轴承系统结构如图1所示。

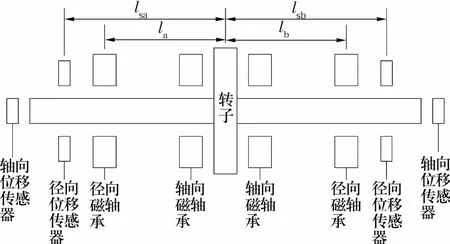
图1 5自由度主动磁悬浮轴承系统结构图Fig.1 Structure of Five-DOF AMB system

根据刚体动量定理和动量矩定理以及磁路分析可得到转子状态方程［7-9］

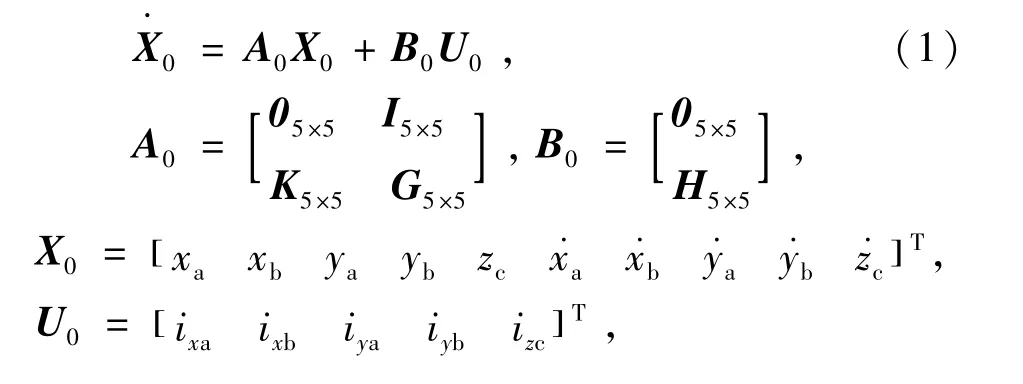
式中：05×5为5阶零矩阵；I5×5为5阶单位矩阵；m为转子质量；Kxx，Kyy，Kzz为磁轴承的位移-力系数；Kix，Kiy，Kiz为磁轴承的电流 -力系数；J为转子绕x，y轴的转动惯量；Jz为转子绕z轴的转动惯量；ω为转子转速；la，lb为转子质心到径向磁轴承中心的距离；xa，xb，ya，yb，zc为转子位移；ixa，ixb，iya，iyb，izc为磁轴承线圈的控制电流。

由于传感器与径向磁悬浮轴承安装于轴向不同位置，通常为非共点安装，使得同一径向平面的2个自由度的输出存在耦合，即传感器输出耦合。由于控制点和测量点不在同一位置，以测量点的位移偏差作为控制量会对系统的动态过程产生影响，在控制中增加对该耦合现象的解耦处理，可以有效改善系统的动态过程。

在刚性转子的情况下，可以通过一定的几何变换实现输出解耦［7］。

根据传感器和径向轴承的几何关系作如下代换

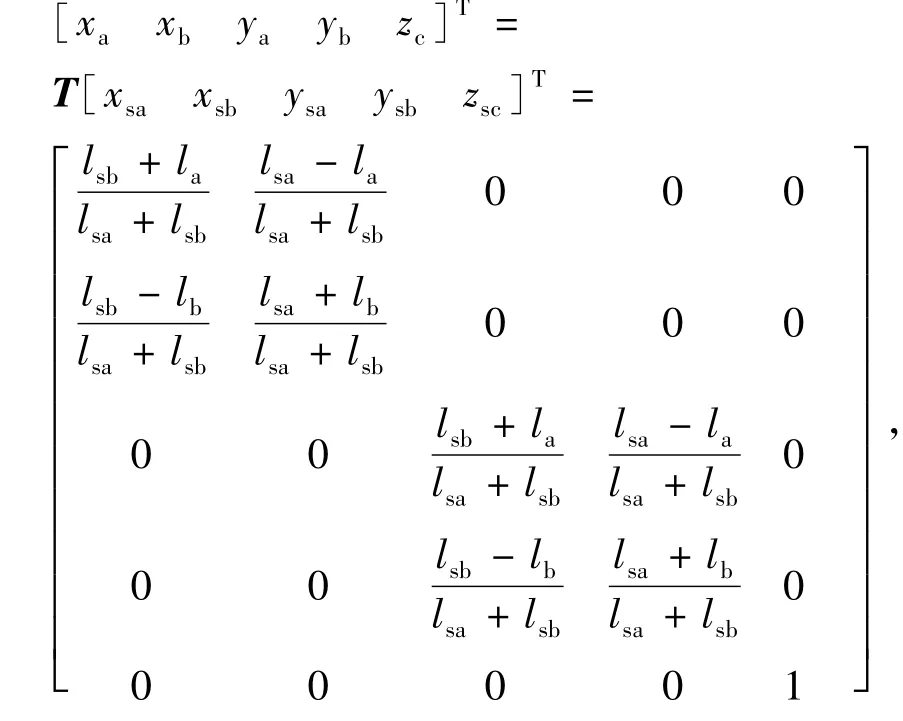
式中：T为转换矩阵；xsa，xsb，ysa，ysb，zsc为转子在传感器位置发生的位移；lsa，lsb为转子质心到径向传感器中心的距离。

输出解耦的状态方程为

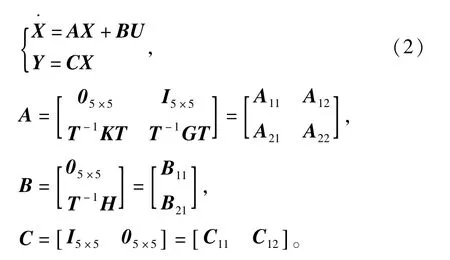
2 积分型滑模变结构控制器的设计

滑模变结构控制是在状态空间设计一个超平面，使其满足可达性，即不管系统状态初始的位置在何处，运动的轨迹都指向超平面。系统一旦到达超平面，控制作用保证系统沿超平面趋向系统原点，这一沿超平面趋向原点的过程称为滑动模态。在这种滑动模态下，系统特性和被控系统参数与外部干扰无关，只取决于所设计的超平面［3］。

滑模变结构控制器的设计主要分为2步：1）确定滑模切换函数；2）设计控制律，保证在切换面上出现滑动模态。

文献［10］提出了一种多输入多输出的变结构控制策略，文献［6］依据该策略，针对4自由度的主动磁悬浮轴承系统设计了一种多输入多输出的积分型滑模变结构控制器。在此基础上，增加轴承的自由度，并对状态方程进行解耦，使得控制器更加符合实际的系统控制要求。

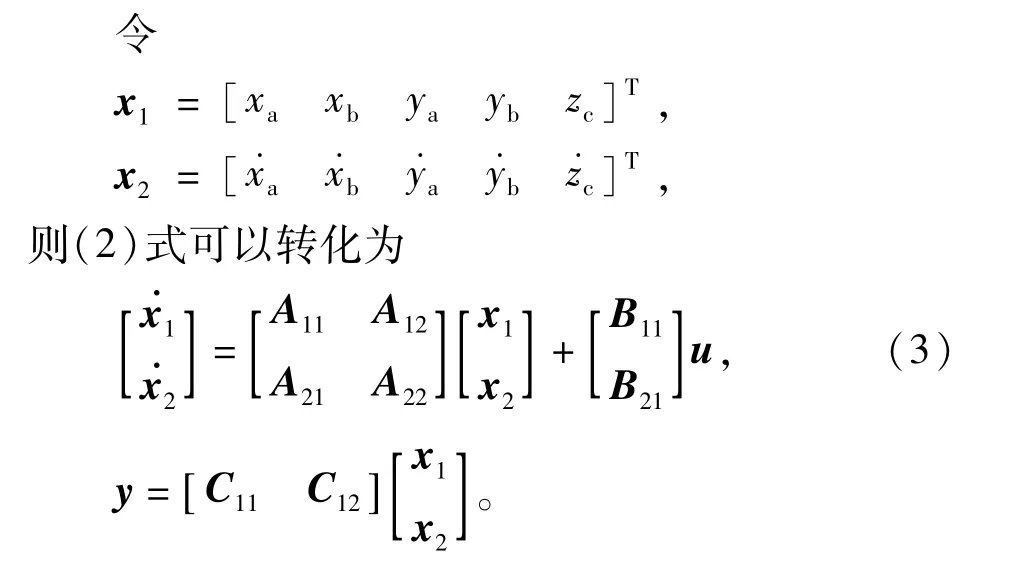
2.1 滑模切换面设计

选取滑模切换面为

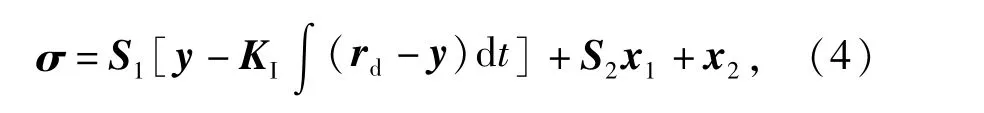
式中：rd为给定输入；S1，S2为5×5的切换面系数矩阵；KI为积分控制的增益矩阵。

由于被控对象是多输入多输出系统，在进行极点配置时较为复杂，该设计保证系统到达滑动模态时，可以通过调整切换面的系数S1，S2，KI对系统的闭环极点进行优化配置［11］；而积分项的引入对于克服扰动有很大的帮助。因此，可以有效地提升系统稳态性能。

2.2 控制器的设计

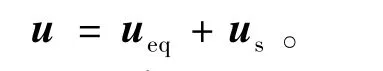
由此可得等效控制函数为

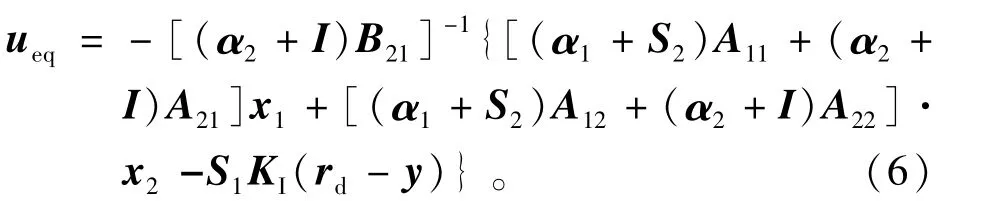
5自由度主动磁悬浮轴承系统是一个非最小相位系统，在能量有限制的条件下，可以加入一个负的调幅值来缩短系统的调节时间，即采用切换函数us，其作用是克服系统模型不确定性以及外界扰动的影响。定义

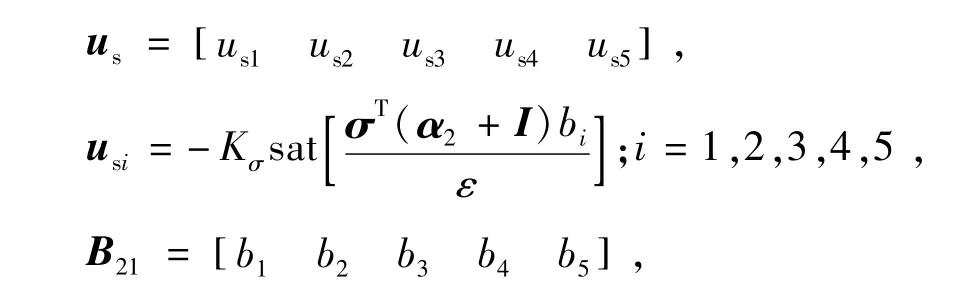
式中：bi为B21的列向量；Ks为开关增益常数；ε为饱和函数的限幅值。此处采用饱和函数而非符号函数，可以有效地减少抖振［12］。

综上，系统控制框图如图2所示。

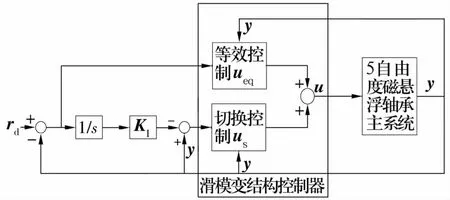
图2 系统控制框图Fig.2 System control block diagram

3 仿真研究

利用MATLAB／Simulink对研究的控制方法进行仿真验证。仿真中，5自由度主动磁悬浮轴承系统的参数设置为：m＝2.756 kg，lsa＝lsb＝0.147m，la＝lb＝0.121 m，Kix＝Kiy＝106.42 N／A，Kiz＝208.38 N／A，Kxx＝ Kyy＝492 860 N／m，Kzz＝690 340 N／m，J＝0.022 96 kg·m2，Jz＝2.069×10-4kg·m2。

滑模变结构控制器的参数设置为：S1＝300I5×5，S2＝2I5×5，KI＝0.3I5×5，Kσ＝10；因此α1＝300I5×5，α2＝05×5；饱和函数的限幅值 ε＝0.000 1；给定输入 rd＝［0 0 0 0 0］T；转子的初始位置为x0＝［3 2-2-3 1］T×10-4。

等效控制模型和切换控制模型分别如图3、图4所示。仿真结果如图5所示，未实现解耦传感器位置导致的耦合时径向4自由度的仿真结果如图6所示，常规PID控制方法的仿真结果如图7所示。

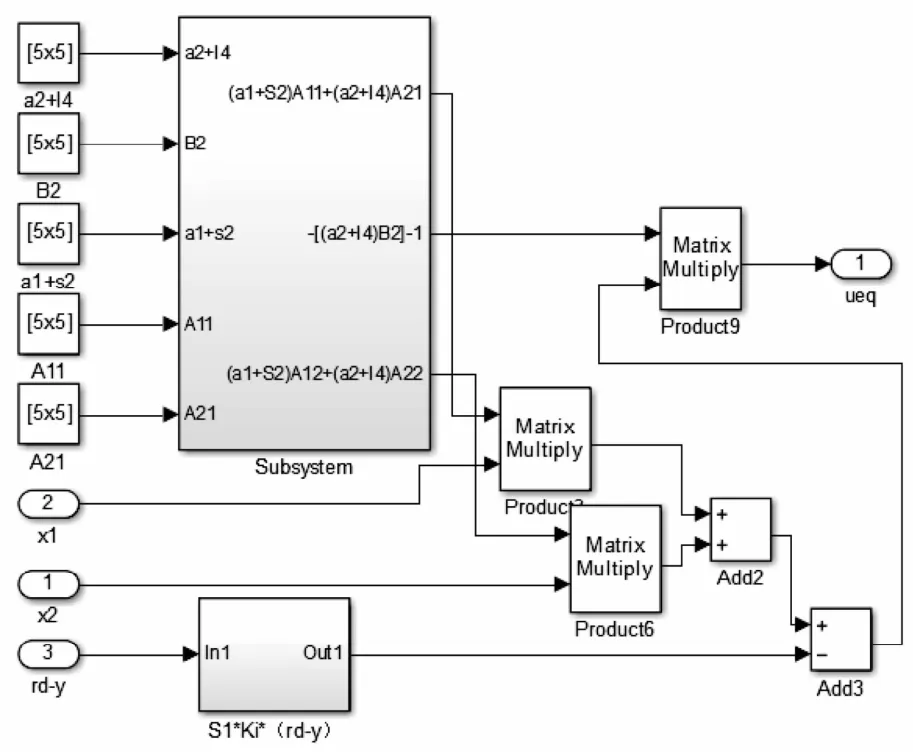
图3 等效控制仿真图Fig.3 Equivalent control simulation model

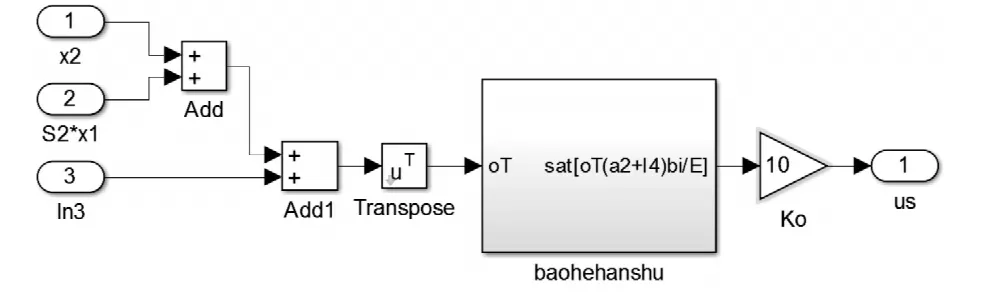
图4 切换控制仿真图Fig.4 Switching control simulation model

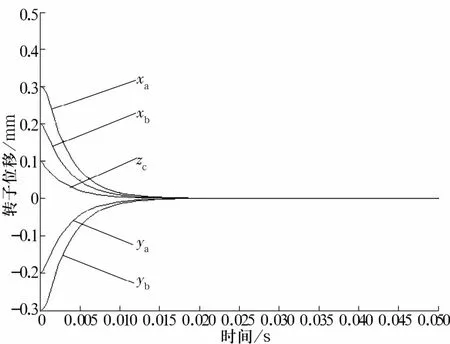
图5 采用积分滑模变结构控制时转子位移Fig.5 Rotor displacements in ISMC

图5 、图7中5条曲线分别代表转子在5个自由度上的位移位置，图6中的4条曲线分别代表转子径向4个自由度的位移，零位置代表转子稳定的悬浮状态。对比图6、图7可以看出，采用未对传感器位置耦合进行解耦的积分滑模变控制可以减小系统的静态误差，但2种控制方法下系统达到稳态所用的时间基本相同；对比图5、图6可以看出，对传感器位置导致的耦合进行解耦后，系统达到稳态所用的时间更短、响应更迅速；对比图5、图7可以看出，与PID控制相比，基于传感器位置解耦的多输入多输出积分滑模变结构控制在5自由度磁悬浮轴承的控制上，静态误差小，鲁棒性更好，响应时间短，无振荡现象。

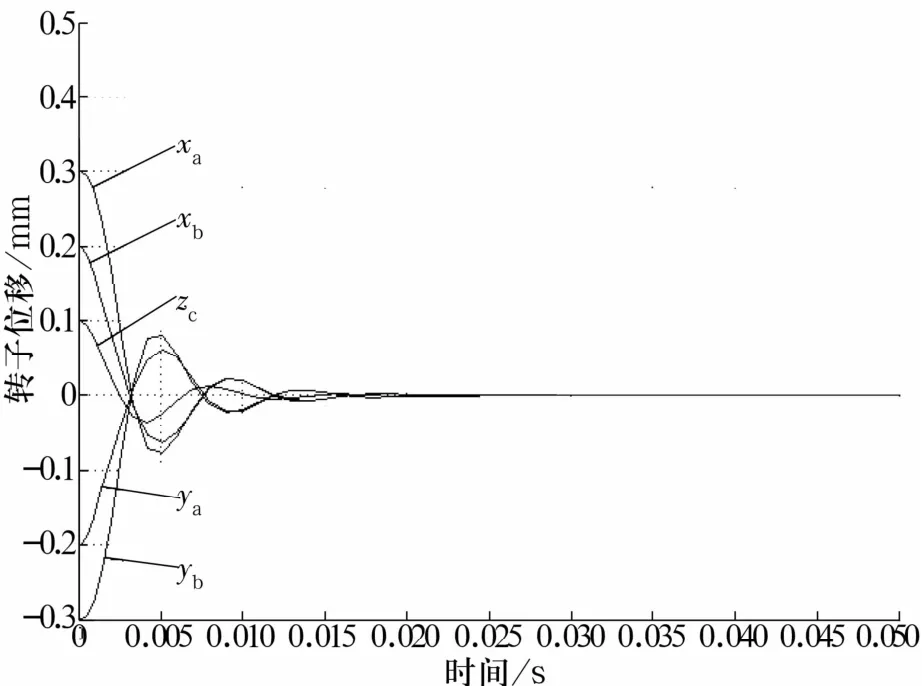
图7 采用PID控制时转子位移Fig.7 Rotor displacements in PID control

4 结束语

针对5自由度主动磁悬浮轴承系统传感器安装位置导致的耦合，设计了多输入多输出积分滑模变结构控制器，利用MATLAB／Simulink进行了PID控制、未对径向传感器位置耦合进行解耦的滑模变结构控制和对传感器位置进行解耦的滑模变结构控制的仿真和对比研究，结果表明，设计的5自由度主动磁悬浮轴承的多输入多输出积分滑模变结构控制器动态性能优越，具有良好的鲁棒性、抗扰动能力和响应速度。