负游隙四点接触球轴承的摩擦力矩计算
2017-07-25韩涛孙立才岳纪东李泽强
韩涛,孙立才,岳纪东,李泽强
(1.洛阳轴研科技股份有限公司,河南 洛阳 471039;2.河南省高性能轴承技术重点实验室,河南 洛阳 471039;3.滚动轴承产业技术创新战略联盟,河南 洛阳 471039)
负游隙四点接触球轴承与成对预紧角接触球轴承在性能上具有相似性,能同时承受轴向载荷、径向载荷和倾覆力矩,可消除轴承内部游隙,从而减小承受载荷时的变形,提高刚度,并降低轴承的体积和重量,故将该类轴承应用到航天执行机构中,能够使部件更加紧凑、轻便。在航天高真空环境条件下,该类轴承采用固体润滑方式,轴承摩擦力矩较大,故应精确控制轴承的摩擦力矩。
1 负游隙理论计算方法
轴承径向游隙仪只能测量正游隙,四点接触球轴承的负游隙不能通过仪器直接测得,只能先通过装配小尺寸球使轴承处于正游隙状态进行测量,然后通过调整球径,根据理论模型计算出所需负游隙。因此合套后轴承的摩擦力矩和刚度等指标在很大程度上受限于模型的准确度。
假定轴承内外圈的垫片角均为β,采用小尺寸试配球时通过测量得到径向游隙为Gr,而最终装配用球与试配用球的直径差为ΔDw,则装配这2种球引起轴承径向游隙的变化如图1所示,其变化量为

图1 球径变化对四点接触球轴承游隙的影响Fig.1 Effect of ball diameter change on the clearance of four point contact ball bearing

则轴承理论径向游隙为

1.1 接触载荷与变形
以QJ1830薄壁四点接触球轴承为例分析,其结构参数见表1。由于套圈为薄壁,在载荷作用下易变形,会影响内部游隙和接触载荷,故必须考虑轴承内外圈尺寸变化对接触载荷的影响。
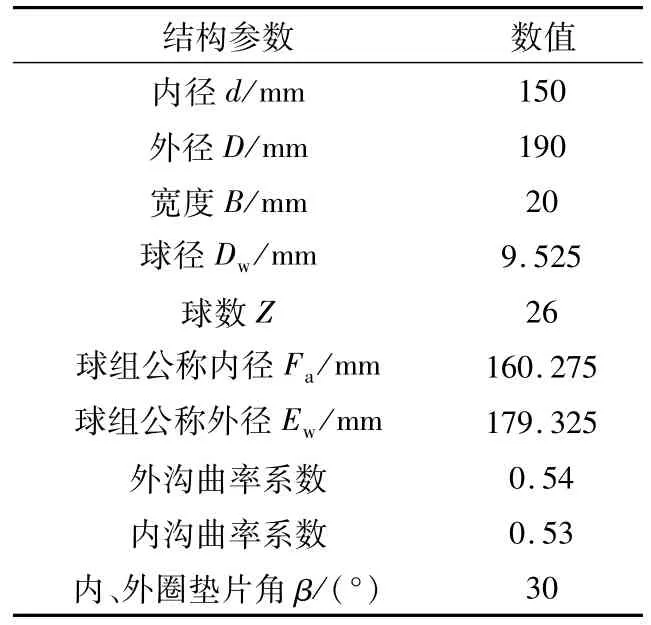
表1 结构参数Tab.1 Structure parameter
轴承内外圈均为薄壁结构,在负游隙状态下球与沟道的4个接触点处存在接触载荷与变形,外圈外径增大,内圈内径减小。根据四点接触球轴承内部几何关系,球与沟道接触点处的变形、径向游隙、外圈外径增大量、内圈内径减小量存在如下关系式
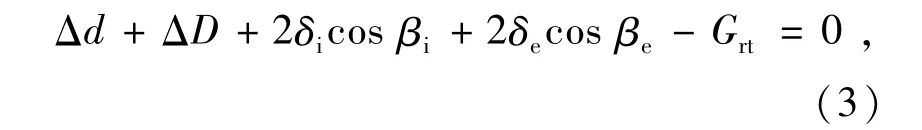
式中:ΔD为外圈外径增加量;Δd为内圈内径减小量;δi,δe为球与内、外沟道之间的接触变形。
1.1.1 套圈尺寸变化量
负游隙状态下,球与沟道处于预紧状态,内外沟道在圆周方向受到球作用的均布载荷,由于试验轴承为薄壁结构,易变形,根据弯曲薄壁圆环经典能量法,可求得内外圈的整体尺寸变化量。负游隙状态时,外圈外径增大量ΔD为
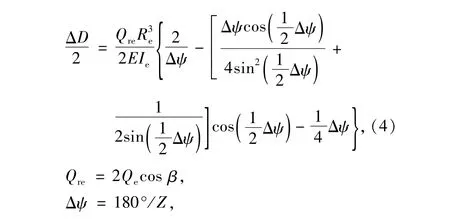
式中:Qre为球与外沟道法向接触载荷的径向分量;Qe为球与外沟道法向接触载荷;Re为外沟曲率半径;E为弹性模量;Ie为外圈惯性矩;Z为球数。
内圈内径减小量Δd为
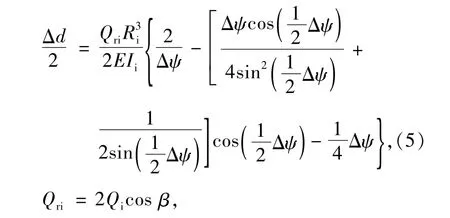
式中:Qri为球与内沟道法向接触载荷的径向分量;Ri为内沟曲率半径;Ii为内圈惯性矩。
1.1.2 球与沟道的法向接触载荷
由Hertz接触理论可知,球与套圈沟道间的法向接触载荷与变形关系为[2]

式中:ki,ke分别为内、外圈接触变形系数。
负游隙四点接触球轴承空载时,球与内外圈间的接触角(αi,αe)分别等于其相应的垫片角(βi,βe),即内外圈接触角相同,而套圈自重造成的球与沟道间的法向载荷与负游隙预载荷相比可忽略不计。假设内外沟道左、右2个接触点处的法向接触力和摩擦力相等,球自转轴线和轴承轴线平行。每个球在沟道4个接触点处法向接触力的作用下均处于平衡状态,则

由(4)~(7)式可求出 Δd,ΔD,δi,δe,Qi,Qe。
1.2 空载状态下摩擦力矩的计算
轴承为固体润滑,转速低,内部摩擦主要为球与内外沟道间的滚动和滑动摩擦。由于工作转速低,球与内外沟道间由于预紧力的作用形成四点接触,球与内外沟道接触点处均存在较大的自旋滑动(图2,ωb为接触区长半轴的点的角速度;i,e分别代表内、外圈)。球相对内外沟道的转动速度可分解为绕接触点切线方向(MM轴)的角速度ωr=ωcosβ和绕接触点法线方向(NN轴)的角速度ωs=ωsinβ(ω为球相对内外沟道的角速度),可以根据角速度矢量合成法计算[2]。ωr为球相对内外沟道的滚动分量,主要产生差动滑动导致的摩擦力矩,在总摩擦力矩中占比较低;ωs为球相对内外沟道的自旋分量,其所引起的滑动而产生的摩擦力矩是轴承旋转时摩擦力矩最主要的来源。
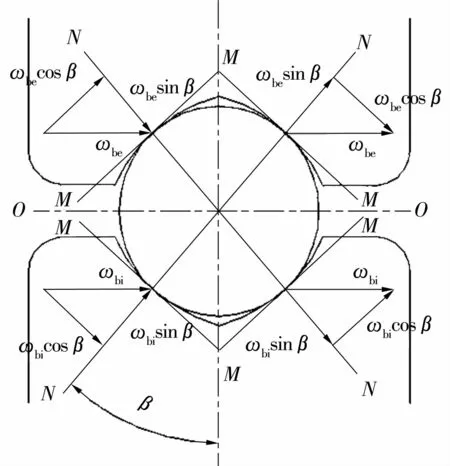
图2 球与沟道接触处的滚动和自旋滑动Fig.2 Rolling and spin sliding at contact point of ball and groove
假设球与内外沟道接触区中各点的滑动摩擦因数均为常数μ,则整体的自旋滑动摩擦力矩为
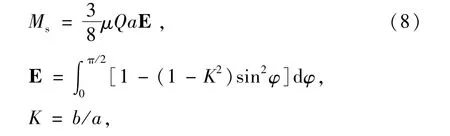
式中:Q为球与沟道接触点处法向力;E为与接触区形状有关的第2类完全椭圆积分;φ为积分变量;K为椭圆偏心率;a,b分别为接触椭圆的长、短半轴。
根据能量守恒定律,并略去轴承内部影响较小的摩擦力,轴承总摩擦损耗为球与沟道接触点处自旋滑动引起的摩擦功耗之和,即
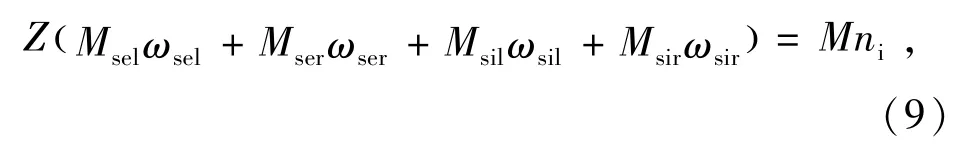
式中:ωsel,ωser,ωsil,ωsir分别为球与内外沟道的角速度自旋分量;Msel,Mser,Msil,Msir分别为球与内外沟道的自旋摩擦力矩,计算方法见文献[2];M为轴承的宏观摩擦力矩;ni为内圈转速。
联立(3)~(9)式可求得轴承的宏观摩擦力矩M。
2 试验验证
试验轴承润滑膜为 MoS2,工艺球(规值 -6 μm)对应的Gr为12μm,选配钢球规值+5μm,理论计算的Gr为-7μm,理论计算的摩擦力矩为0.154 N·m,保持架材料为PTFE05。对装配前后的内、外径进行测量,对镀MoS2膜的轴承在200 N轴向载荷、100 r/min转速下正、反面分别跑合30 min,并监测跑合过程中的动态摩擦力矩,然后测试启动摩擦力矩。
MoS2磁共离子溅射固体润滑薄膜具有低摩擦因数、耐磨损以及较高的承载能力,主要原因在于多组元离子之间的协同效能能够致密化润滑膜的表面和断面组织结构。而溅射薄膜通过沉积得到,在薄膜与基体材料交界处形成的润滑薄膜最为致密,当达到一定厚度后,膜的生长方式就会发生变化,最后在膜的顶层生成的是柱状或针状疏松组织结构,既影响其润滑性能,又容易吸潮、氧化和剥落。
对沟道溅射成膜的轴承进行预跑合则可改善该工况,并能提高润滑膜的润滑性能。跑合是一个磨合期,使轴承在装机使用前预先达到良好的运行状态,从而提高装机使用中的可靠性。通过跑合,球与沟道接触带润滑薄膜的顶层疏松结构将随球的挤压滚动而剥落,而底层薄膜在压力作用下会更加致密。
轴承跑合后,通过调整球径规值获得-9~-3 μm的负游隙,然后进行动态摩擦力矩的测试,结果见表2。由表2可知,实测值比理论值大,因为理论计算只考虑了最主要的自旋滑动产生的摩擦力矩,负游隙值越大,其在全部摩擦力矩中所占比重也越大,所以理论计算值随着负游隙值的增加越来越接近于实测值。考虑到摩擦力矩的影响因素较多,固体润滑轴承摩擦力矩测试值一般有30%左右的波动,故模型的计算误差在允许范围之内。
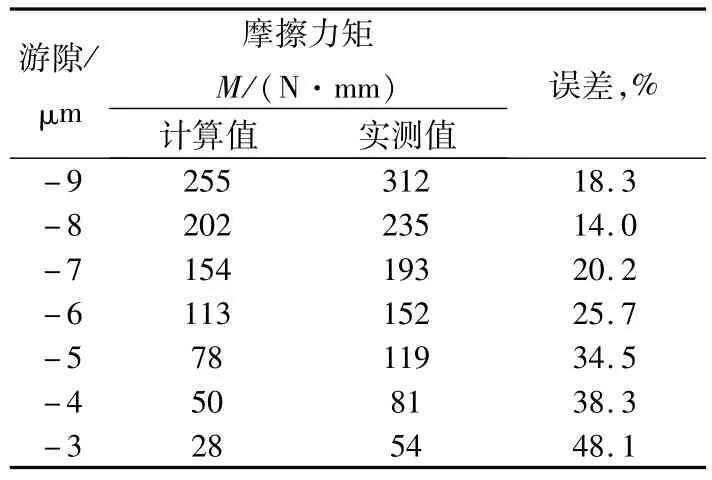
表2 不同游隙下的摩擦力矩值Tab.2 Friction torque values under different clearance
3 结论
1)根据负游隙四点角接触球轴承的内部几何关系求得负游隙的计算方法。
2)摩擦力矩的理论计算模型可以根据能量守恒定律计算。
3)当游隙小于-6μm时,摩擦力矩的理论计算值相对实测值的误差小于30%。
