圆柱滚子轴承保持架兜孔尺寸误差对运动精度的影响

李占立，李济顺,2，余永健,2，薛玉君,2，马伟,2

(1.河南科技大学 机电工程学院，河南 洛阳 471003;2.河南省机械设计及传动系统重点实验室，河南 洛阳 471003)

滚动轴承是机械传动中广泛应用的基础件，其性能优劣对设备运转会产生重大的影响。轴承的运动精度是评价轴承质量的重要指标之一。文献[1]采用数值模拟法分析了轴承零件的几何误差与轴心轨迹之间的关系，并通过试验加以验证。文献[2-3]研究了钢球和外圈的波纹度与轴心之间的关系。文献[4]分析了深沟球轴承套圈的圆度误差和钢球的尺寸误差与轴承非重复性跳动之间的关系，但没有考虑保持架的影响。文献[5]建立了考虑滚动体尺寸误差时准确计算轴承中心的数学模型，主要研究滚动体误差的大小和误差滚动体的数目对轴心轨迹的影响。文献[6]采用坐标变换法建模，通过模拟与数值仿真相结合，研究了套圈的圆度误差、滚动体的直径误差对旋转精度的影响。文献[7]对影响大中型精密圆锥滚子轴承旋转精度的因素进行了分析,保持架兜孔的尺寸误差是影响轴承运动精度的因素之一。

以圆柱滚子轴承为研究对象，根据轴承零件间的运动关系,建立引入保持架兜孔尺寸误差的数学模型。对轴承的运动状态进行模拟和数值分析，研究保持架单个和多个兜孔的尺寸误差及保持架兜孔尺寸误差的排布方式对轴承运动精度的影响规律。

1 圆柱滚子轴承数学模型

1.1 数学模型的假设

为便于计算，建立轴承数学模型时假设：1)仅考虑保持架兜孔的尺寸误差和内圈的圆度误差，其他零件均为理想尺寸；2)不考虑温度变化和轴承内部润滑油膜厚度的影响；3)轴承转动过程中，滚子不发生歪斜，与内、外圈之间的运动为纯滚动,不存在滑动，且与滚道完全接触；4)外圈始终静止，内圈沿逆时针方向旋转。

1.2 轴承零件误差的简化

轴承转动过程中，滚子在兜孔中的位置不同，承载区滚子的速度将超前于保持架，推动保持架向前运动， 滚子在兜孔中的位置如图1所示。图中，φ为1#滚子与x轴正半轴的夹角;φ为滚子的位置角。

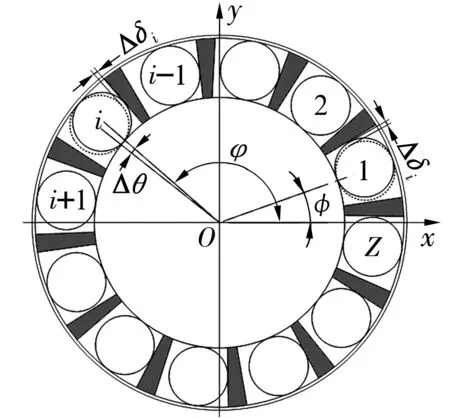
图1 滚子在兜孔中的位置

1)保持架兜孔的尺寸误差

实际加工的保持架兜孔存在尺寸误差，且每个兜孔尺寸误差不同，如图1所示。 保持架兜孔间尺寸误差可表示为

[Δδ]=[Δδ1,…,Δδi,…,ΔδZ]T，

(1)

保持架兜孔的实际尺寸为

[Lw]=[Lw1,…,Lwi,…,LwZ]=

[Lr+Δδ1,…,Lr+Δδi,…,Lr+ΔδZ]T

，(2)

式中：Lr为兜孔的理想尺寸；Δδi为第i个兜孔的尺寸误差；Z为滚子个数。

理想情况下滚子均布在滚道上，由于保持架兜孔的尺寸误差，滚子在滚道上的位置将会改变，兜孔尺寸误差处的滚子与x轴正半轴之间的夹角将发生变化，其变化量为

Δθ=2Δδi/Dpw，

(3)

式中：Dpw为滚子组节圆直径。

2)内圈的圆度误差

圆度误差是指同一横截面内回转体实际轮廓对理想圆的最大变化量，是有周期性的一条封闭的几何曲线，用Fourier级数形式可表示为

式中：θ为滚道上点的位置角；M为内圈滚道圆度误差最大的谐波阶数；Am，Bm分别为m阶谐波分量的正、余弦系数。

内圈滚道轮廓的实际曲线可表示为一个标准圆和圆度误差的叠加，则内圈滚道的曲线方程可表示为

s(θ)=di+R(θ)。

(5)

式中：di为内圈滚道直径。

1.3 建立坐标系

假设套圈滚道的几何中心与滚动体节圆的中心相重合，为准确描述轴承内部零件间的运动关系，建立外圈的整体坐标系Oxy和内圈的局部坐标系Oxiyi，将圆柱滚子轴承放到所建立的坐标系中进行分析,如图2所示。图中，β为内圈转过的角度;ρ为内圈滚道的极半径。

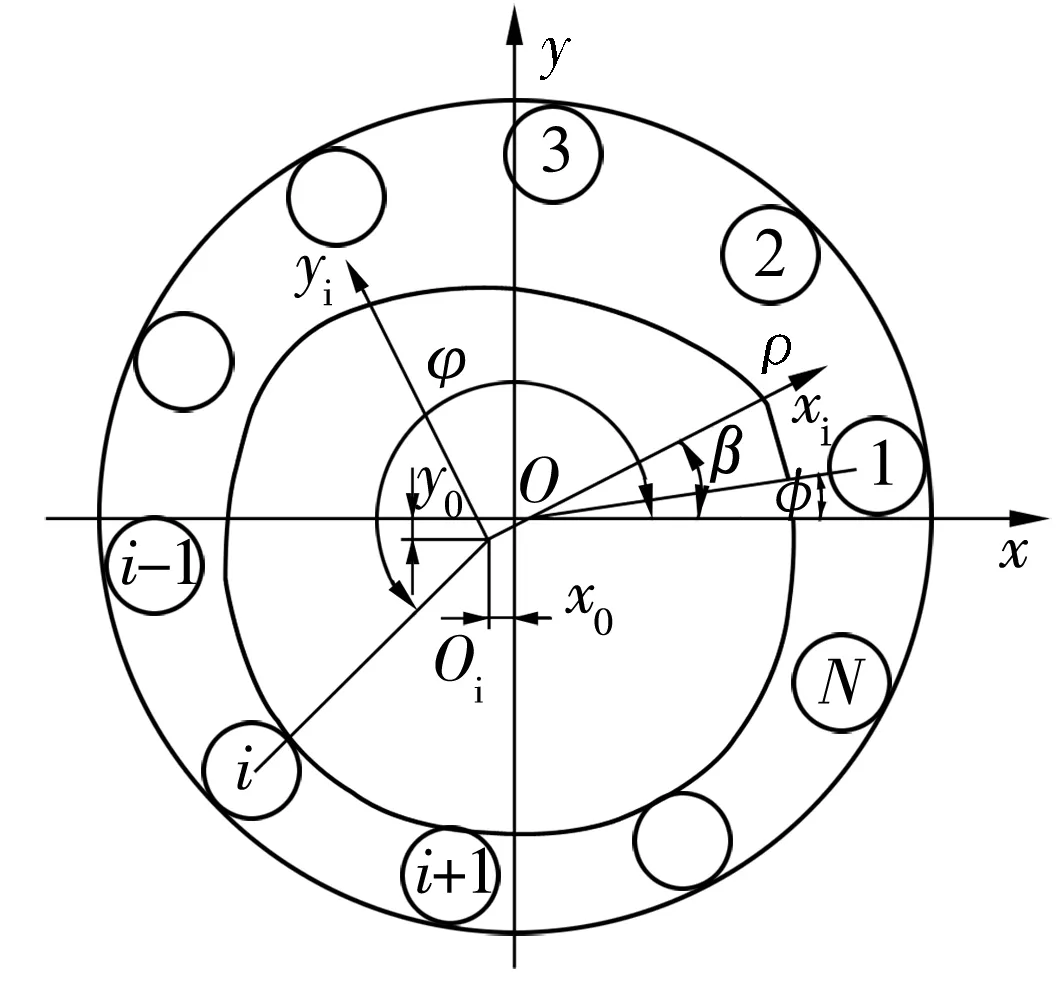
图2 直角坐标系

在局部坐标系下,内圈滚道曲线的参数方程为

(6)

在整体坐标系下，内圈滚道的曲线方程可表示为

(7)

式中：x0，y0为局部坐标系原点相对于整体坐标系原点的变化量。

1.4 轴承零件的运动几何关系

外圈不动，内圈逆时针转动。滚子公转的角度γ与内圈的转动角度β之间的关系为[8]

(8)

式中：Dw为滚子直径。

设x轴正上方距离x正半轴最近的滚子为第1个滚子，当内圈沿逆时针方向转动j个β角度时，第i个滚子与x轴正半轴之间的夹角为

(9)

内圈转动j个β角度时，第i个滚子在整体坐标系下的圆心坐标为

(10)

式中：de为外圈滚道直径。

内圈滚道的曲线方程变为

(11)

滚子与内圈接触时，滚子圆心到内圈滚道曲线的距离为[9]

(12)

1.5 轴承运动精度的评价指标

内圈转动过程中，每转动1°，都会对应一个圆心坐标(x0，y0)，轴承运动精度的评价指标内圈径向跳动为[10]

Kia=ymax-ymin，

(13)

式中:ymax，ymin分别为内圈圆心在y方向的最大值和最小值。

2 数学模型求解

根据所建立的数学模型，对圆柱滚子轴承的运动状态进行仿真分析，其流程图如图3所示。

1)设定相关参数

输入圆柱滚子轴承相关的结构参数，如内径di、外径de、滚子个数Z、滚子直径Dw、径向游隙Pd、保持架兜孔的尺寸误差Δδi等。

2)判断滚子与内圈是否发生干涉

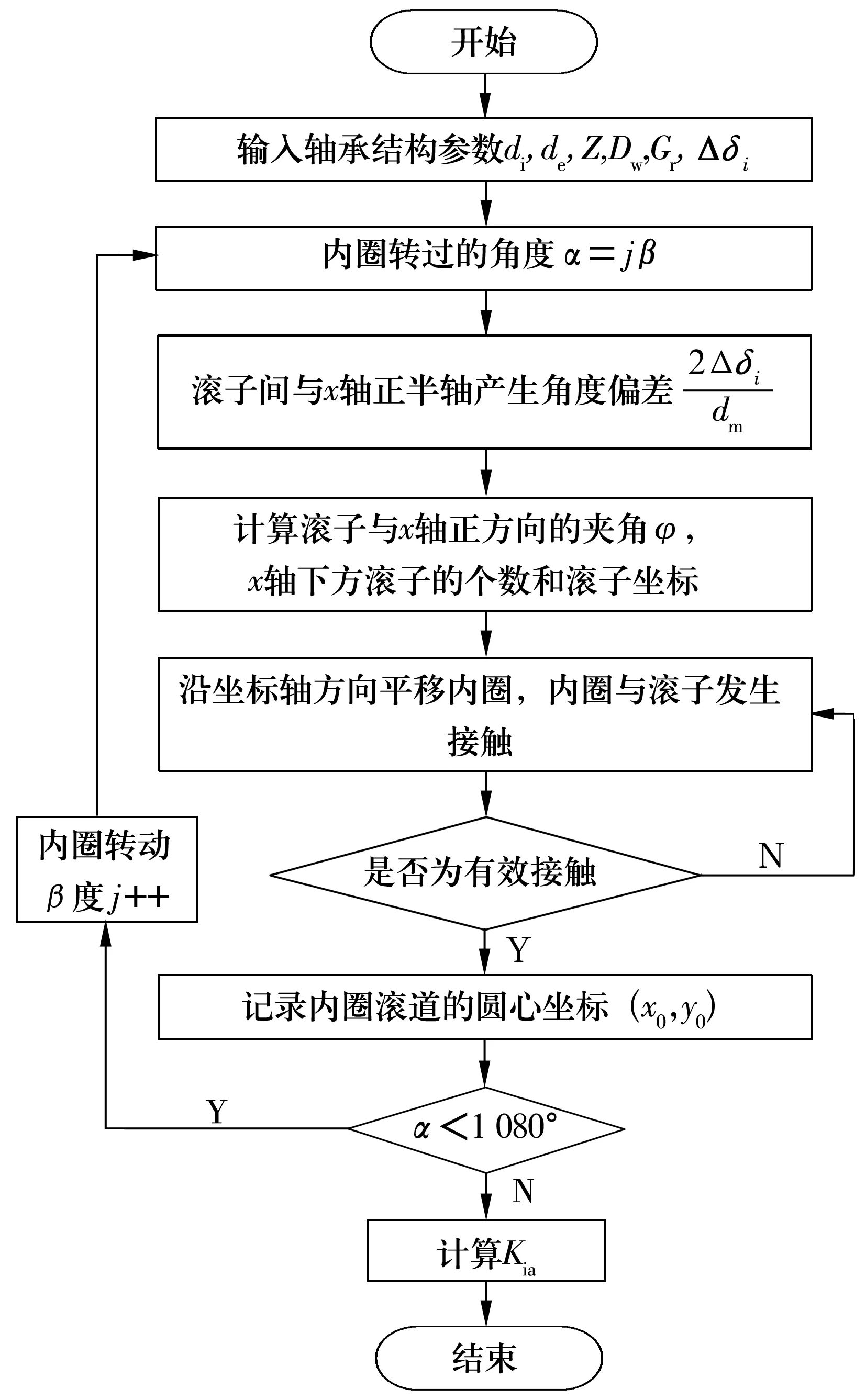
图3 仿真流程图

仿真过程中,内圈以一定的步长在给定的网格区域内平移时，还需要判断滚子与内圈是否发生干涉，通过计算x轴下方所有滚子圆心到内圈滚道曲线的最短距离t[i]来判断，Eps为容许的误差值(取圆度误差值的0.1%)。若t[i]<ε=Dw-Eps，则滚子与内圈发生干涉；若x轴下方所有的滚子均满足t[i]>ε,则认为该位置内圈与滚子不发生干涉。

3)判断滚子与内圈是否有效接触

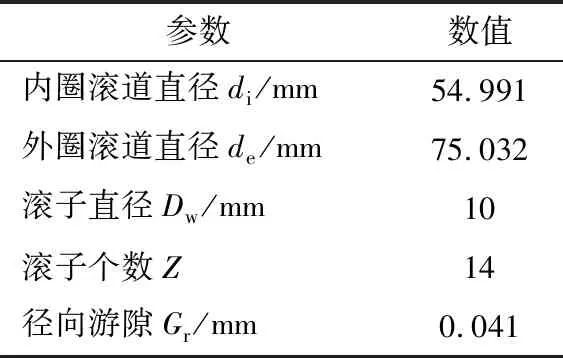
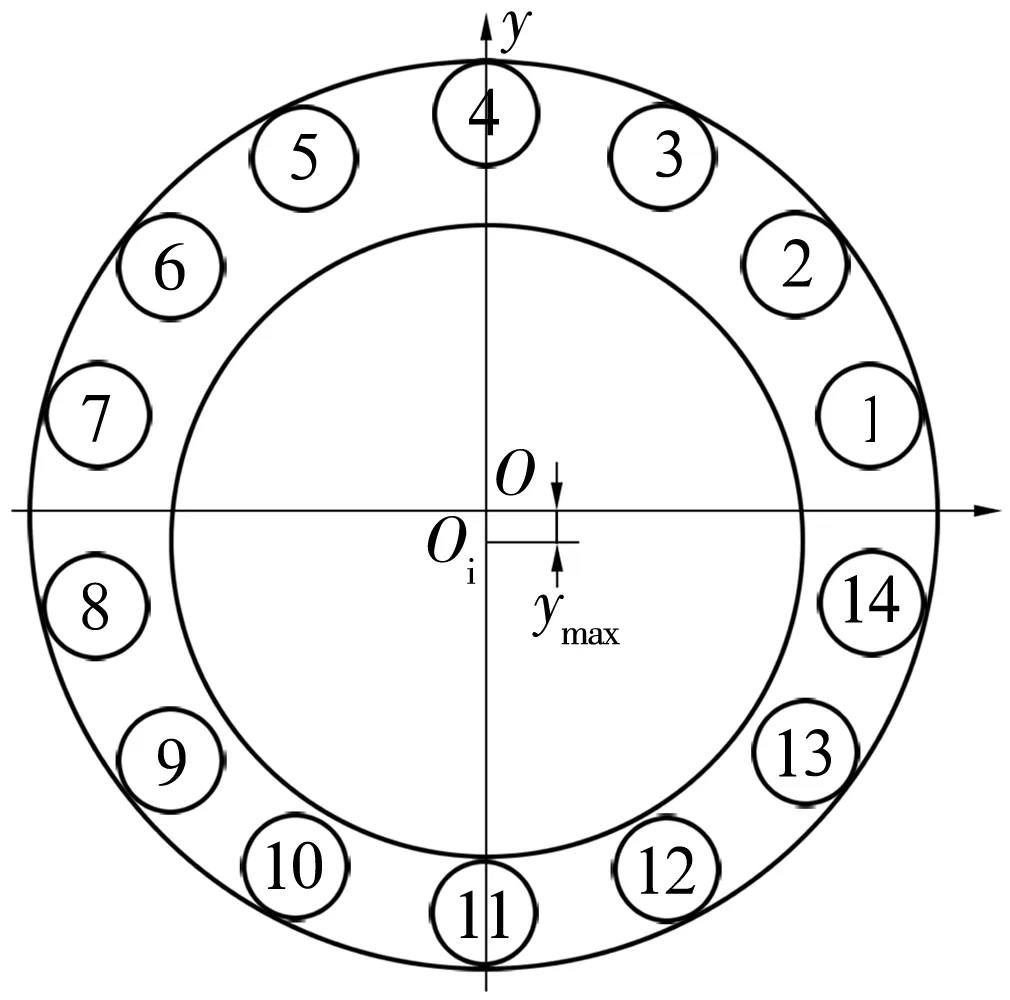
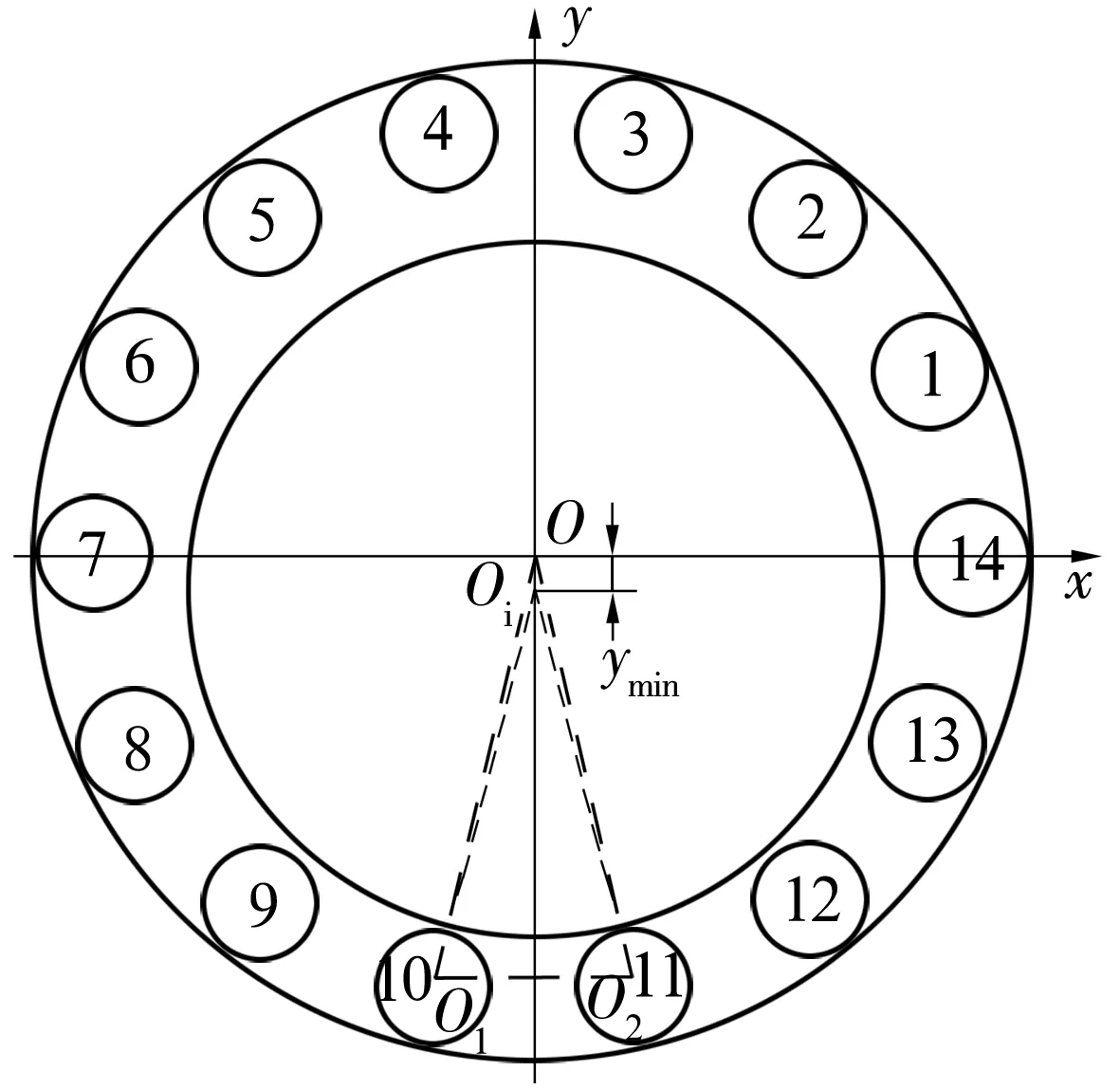
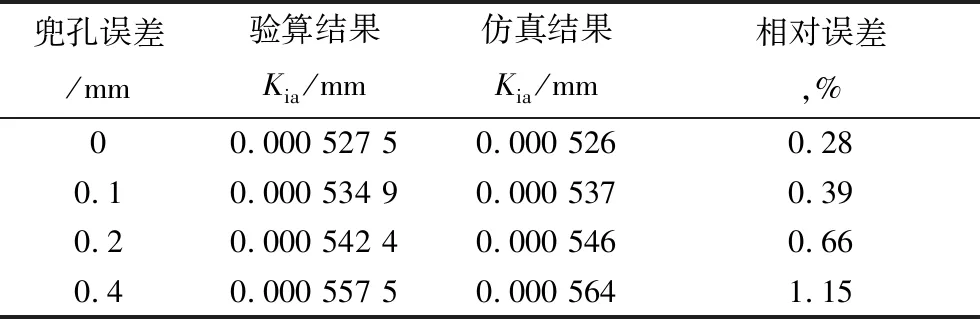
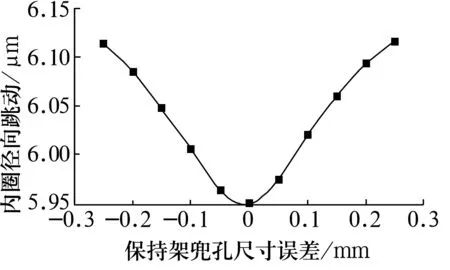
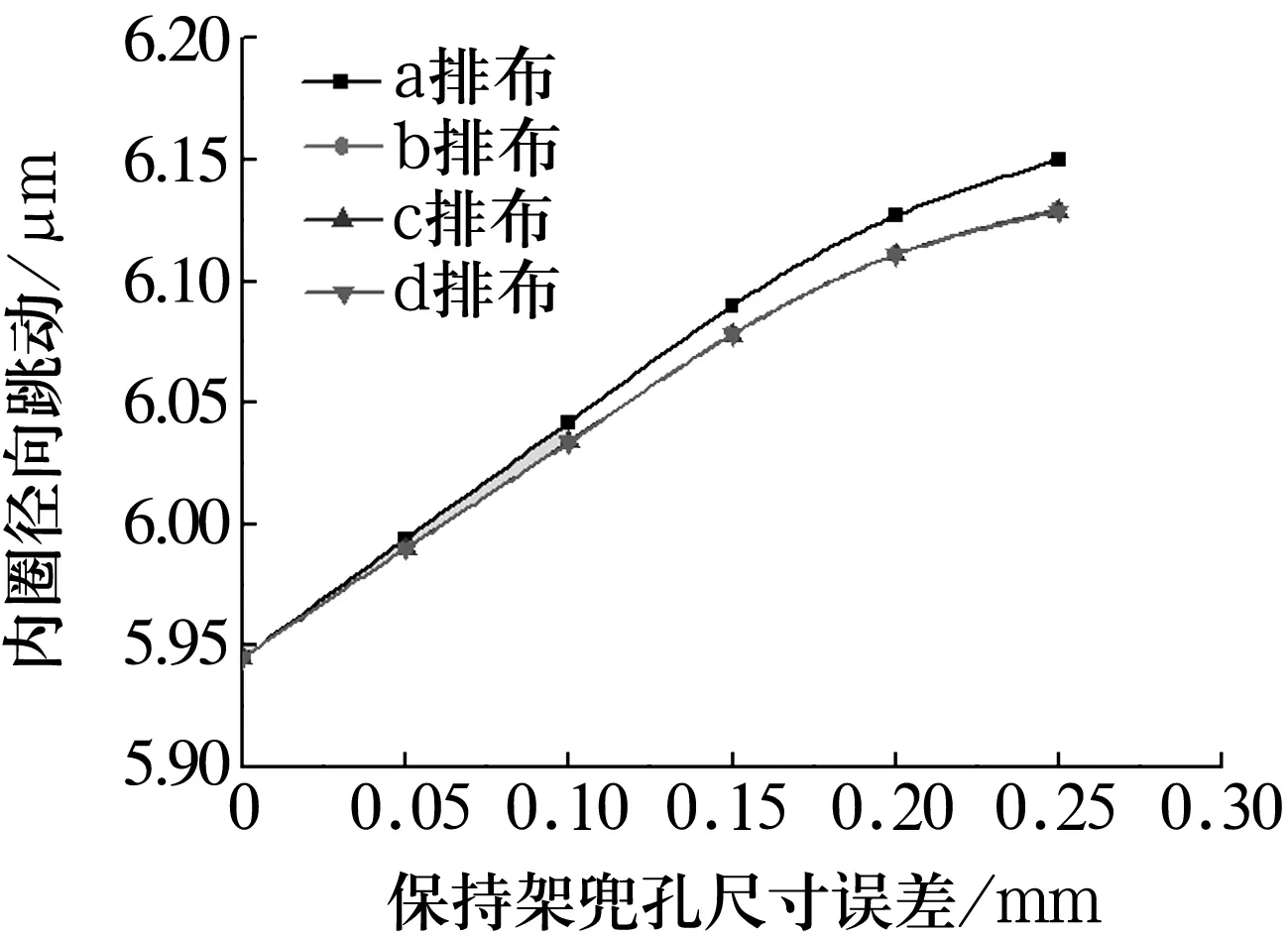
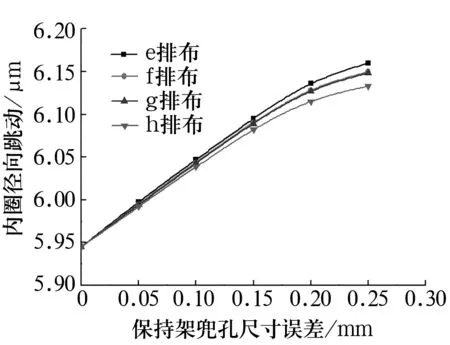
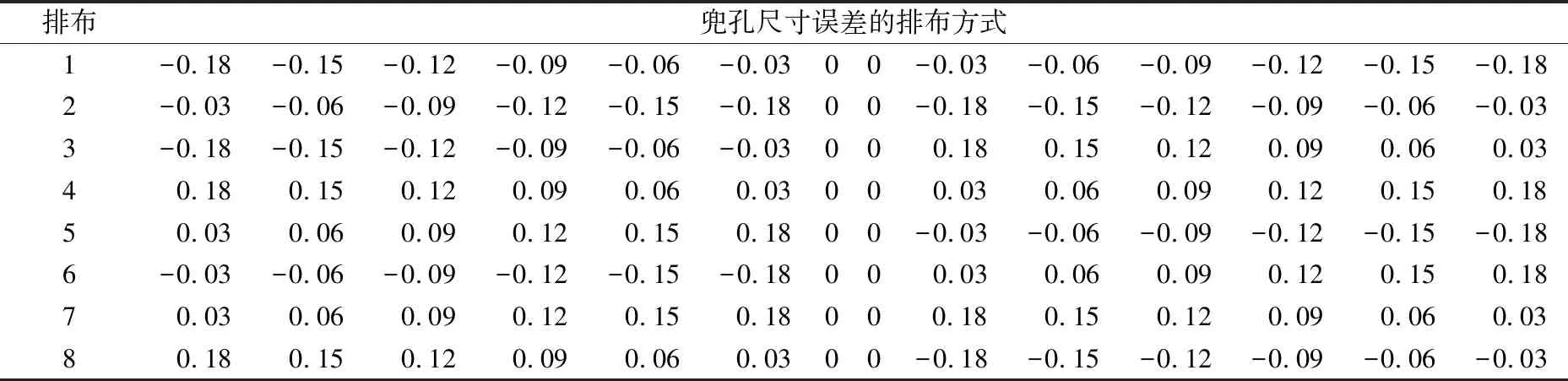
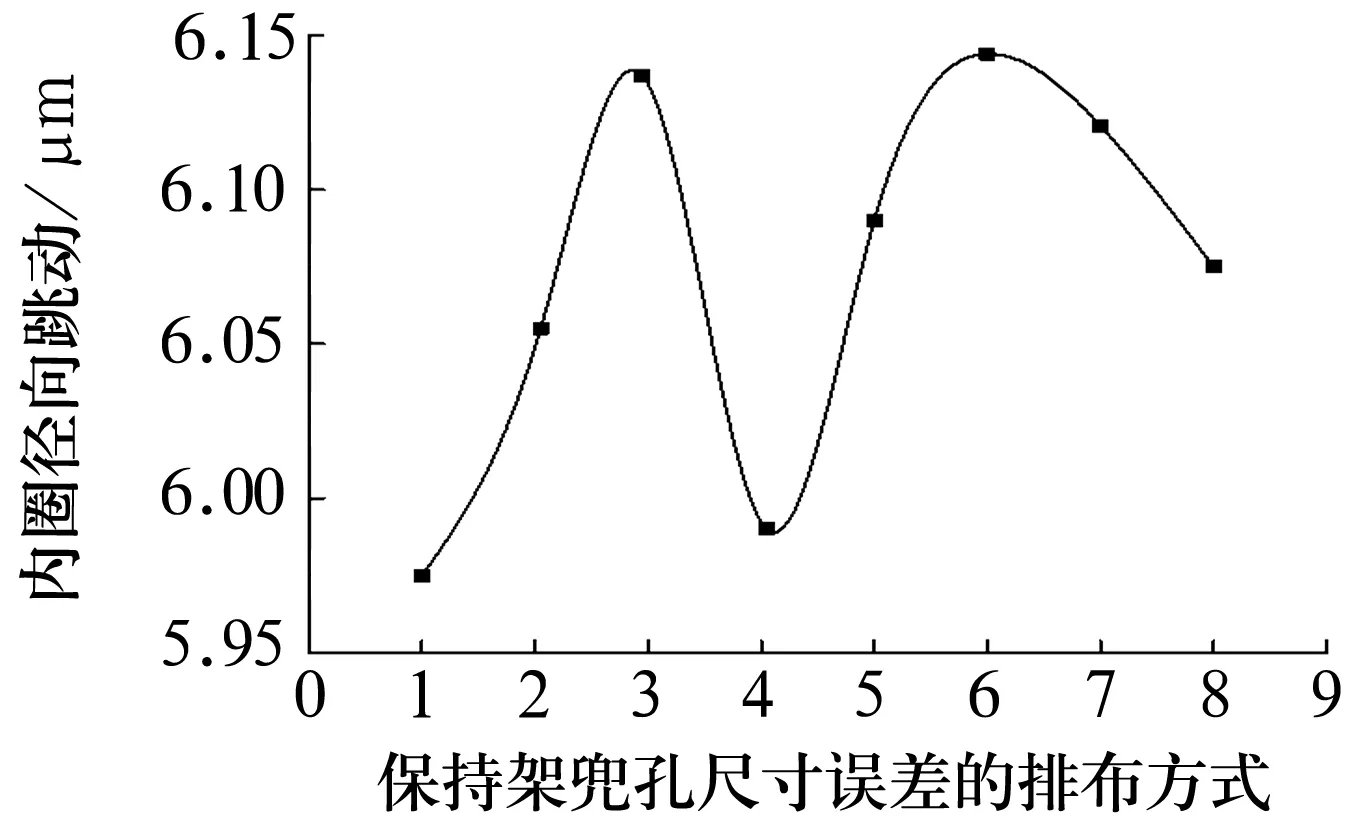
先计算|t[i]-Dw|，若满足|t[i]-Dw|

4)最优的稳定状态

内圈在平移的过程中,可能存在多个圆心坐标使滚子与内圈滚道发生有效接触，因此需要求出内圈最容易达到稳定状态的圆心坐标。将每组有效接触滚子的圆心与内圈的圆心相连，如图4所示,通过比较其斜率之和的绝对值|K|确定最佳的圆心坐标。

(14)

式中：ki为第i个滚子与内圈接触时滚子圆心与内圈圆心相连的斜率。

图4 内圈稳定状态的判定

K越小，内圈在该圆心位置所受到合力的方向与y轴之间的夹角就越小,内圈就越容易达到稳定状态。

5)仿真程序验证

根据仿真程序可得到内圈的径向跳动值，但还需验证其正确性，可使滚子和内圈处于某个特殊的位置来验证。假设套圈和滚子均为理想尺寸，保持架单个兜孔存在尺寸误差。圆柱滚子轴承结构参数见表1。

表1 圆柱滚子轴承参数

当滚子位于y轴正下方(图5)，内圈与最下方的滚子接触时，内圈滚道的圆心坐标取最大值ymax=-0.020 5 mm。10#，11#滚子关于y轴对称(图6)，当内圈与10#，11#滚子接触时，内圈滚道的圆心坐标取最小值ymin。假设仅10#兜孔存在尺寸误差0.3 mm,其他兜孔均为理想尺寸，由(3)式可求得10#，11#滚子之间夹角的变化量为0.009°。10#滚子的圆心坐标为x10=-10.190 592 562 3，y10=-30.877 857 426；同理11#滚子的坐标为x11=-x10，y11=y10。

图5 内圈圆心坐标最大值的位置

图6 内圈圆心坐标最小值时的位置

在等腰三角形OiO1O2中

(15)

由(15)式求得内圈的圆心坐标为(0,-0.021 049 9)。根据所求的圆心坐标判断内圈滚道是否与第8#，9#，12#，13#滚子发生干涉。可得Kia=ymax-Δy= 0.000 549 9 mm,仿真结果Kia0=0.000 555 mm,相对误差为0.92%。

当保持架单个兜孔的尺寸误差分别为0，0.1，0.2，0.4 mm时，内圈径向跳动值的验算结果与仿真结果对比见表2。

表2 2种结果的对比

由表2可知，仿真结果和计算结果基本吻合，误差相对较小，证明该算法能够较准确地预测保持架兜孔的尺寸误差对轴承运动精度的影响。

3 算例分析

以某圆柱滚子轴承为例(结构参数同表1)，通过上述数学模型分析保持架兜孔的尺寸误差对轴承运动精度的影响。

3.1 单个兜孔尺寸误差与轴承运动精度关系

3.1.1 仅考虑兜孔尺寸误差的计算结果

保持架兜孔存在尺寸误差时，误差处的滚子与其他滚子之间的夹角将会发生变化。当兜孔尺寸误差处的滚子与套圈发生稳定接触时，会对轴承的运动精度产生一定的影响。假设保持架单个兜孔存在尺寸误差，其他零件均为理想尺寸。内圈转动过程中，保持架随内圈转动发生公转。内圈的径向跳动随兜孔尺寸误差的变化如图7所示。

图7 兜孔尺寸误差与内圈径向跳动关系

由图7可知，当保持架兜孔尺寸误差为负时，随兜孔尺寸误差的减小，内圈的径向跳动呈线性增加。当兜孔的尺寸误差为正时，随兜孔尺寸误差的增大，内圈的径向跳动呈线性增加。兜孔的尺寸误差为正和负时，内圈的径向跳动值曲线对称，兜孔尺寸的正、负误差对轴承运动精度的影响一致。兜孔为理想尺寸时，内圈的径向跳动值为0.000 527 5 mm，当保持架兜孔的尺寸误差为0.3 mm 时，内圈的径向跳动为0.000 555 mm，两者相差较小，故保持架单个兜孔尺寸误差对轴承运动精度影响较小。

3.1.2 考虑内圈圆度误差的计算结果

为了研究内圈有圆度误差的情况下，单个兜孔的尺寸误差对轴承运动精度的影响。设内圈滚道的Fourier级数谐波分量R(θ)=μ/2cos(10θ)，圆度误差μ=6 μm，滚子和外圈均为理想尺寸。

由图8可知，当保持架兜孔的尺寸误差为负时，随兜孔尺寸误差减小，内圈的径向跳动增大,轴承的运动精度变差。当兜孔尺寸误差为正时，内圈径向跳动值随兜孔尺寸误差的增加而变大，且其增加趋势逐渐变缓,兜孔的尺寸误差越大，对轴承运动精度越不利。兜孔尺寸误差为正和负时，内圈的径向跳动曲线近似对称，由此可知，保持架在单个兜孔存在尺寸误差的情况下，兜孔的正、负误差对轴承运动精度的影响基本相同。

图8 单个兜孔尺寸误差与内圈径向跳动关系

3.2 2个兜孔尺寸误差与轴承运动精度关系

为研究保持架2个兜孔存在尺寸误差对轴承运动精度的影响，现给出2个兜孔有尺寸误差时的排布方式见表3(A为保持架兜孔的尺寸误差值)。由兜孔尺寸误差的排布方式及所建立的圆柱滚子轴承的数学模型，可知兜孔尺寸误差的排布方式与轴承内圈径向跳动的关系如图9所示。

表3 2个兜孔尺寸误差的排布

图9 2个兜孔的排布与内圈径向跳动关系

从图9可以看出，4种排布方式中，a排布的内圈径向跳动最大，b，c，d排布的径向跳动值相同，说明了这3种排布对运动精度的影响相同。其中,a排布为2个误差的兜孔相邻，b，c，d排布为2个误差的兜孔不相邻，当兜孔误差处的滚子与内圈和外圈构成稳定接触时，a排布中滚子间夹角的变化量最大，故该排布内圈径向跳动也最大。

3.3 3个兜孔尺寸误差与轴承运动精度关系

为研究保持架3个兜孔存在尺寸误差对轴承运动精度的影响，现给出3个兜孔存在尺寸误差时的排布方式见表4( A为兜孔尺寸误差值)。3个兜孔尺寸误差的排布方式与轴承内圈径向跳动的关系如图10所示。

表4 3个兜孔尺寸误差的排布方式

图10 3个兜孔的排布与内圈径向跳动关系

由图10可知，内圈的径向跳动与保持架兜孔尺寸误差值及误差兜孔之间的排布方式有关。在4种排布方式中，e排布的内圈径向跳动值最大，f，g排布次之，h排布最小；这是由于f排布为3个有尺寸误差的兜孔相邻，当兜孔尺寸误差处所对应的滚子与套圈构成有效接触时，滚子之间的夹角变化量最大，内圈的圆心坐标在y方向上的变化量也最大，轴承的径向跳动值最大。而h排布中当兜孔尺寸误差处的滚子构成有效接触时，其间夹角的变化量最小，内圈径向跳动值也最小，此排布轴承的精度最优。

3.4 多个兜孔尺寸误差与轴承运动精度关系

为分析保持架多个兜孔尺寸误差的排布方式对轴承运动精度的影响，考虑保持架兜孔的尺寸误差按一定的规律排列，其排布方式见表5。保持架兜孔尺寸误差的排布方式为：从2个尺寸误差为0的兜孔向两侧逐渐增加或减小，能够反映保持架兜孔的排布方式对轴承径向跳动的影响。

表5 多个兜孔尺寸误差的不同排布

由图11可知,保持架兜孔尺寸误差的排布方式对轴承内圈径向跳动的影响不同。1，3，5,7排布为从尺寸误差为0的兜孔向两侧逐渐减小；2，4，6，8排布为从尺寸误差为0的兜孔向两侧逐渐增加。在1～8组的排布中，排布1为径向跳动最小的误差组合，排布6为最大组合。在排布6中，尺寸误差为0的兜孔左侧，尺寸误差为正，右侧为负。当左、右两侧兜孔处的滚子与套圈稳定接触时，滚子间的夹角变化量最大，此时内圈的径向跳动值最大。而排布1中，尺寸误差为0的兜孔两侧，兜孔尺寸误差的情况相同，在此种排布方式下，两侧兜孔处的滚子间夹角变化量最小,对内圈径向跳动的影响也最小。

图11 多个兜孔排布与内圈径向跳动关系

4 结束语

基于所建立的圆柱滚子轴承数学模型，通过MATLAB进行编程仿真，并验证了该仿真算法的正确性，研究了保持架兜孔的尺寸误差对轴承运动精度的影响规律。结果表明：随着保持架兜孔尺寸误差的增加,内圈的径向跳动值增大；保持架兜孔尺寸误差对轴承运动精度会产生一定的影响，但影响有限；保持架兜孔尺寸误差的合理排布可以减小轴承内圈的径向跳动，提高轴承的运动精度。所提出的算法可以有效地预测轴承的运动精度，为设计和开发高精度轴承提供理论指导。