判别式法巧证几个著名的不等式
2017-07-25广州市第二中学510530张先龙
广州市第二中学(510530) 张先龙
判别式法巧证几个著名的不等式
广州市第二中学(510530) 张先龙
判别式来源于一元二次方程根的个数的判断,可用于求函数的定义域、值域和最值,也可用于证明不等式等等,是解题中十分基本而非常重要的数学技巧.作为配方法的一种集成性工具,有时使用起来颇为方便,它在不等式证明中屡建奇功,本文拟给出几个著名的不等式的判别式证法,供读者参考.
1.Cauchy不等式
设 a1,a2,···,an,b1,b2,···,bn为两组实数,则
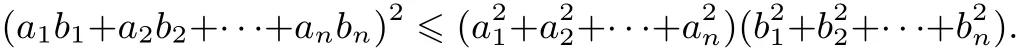
证明 (1)当ai全为0时,命题显然成立;
(2)当ai不全为0时,有构造二次函数

2.嵌入不等式
设x,y,z是任意实数.A,B,C是任意三角形的三个内角,求证:
x2+y2+z2>2xy cosA+2yz cosB+2zxcosC.当且仅当时等号成立.
证明将原不等式转化为
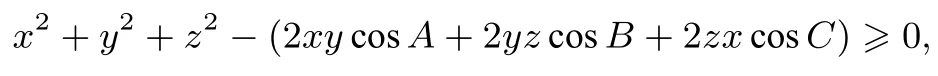
构造二次函数
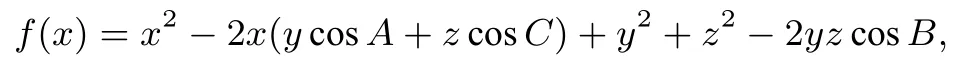
因为
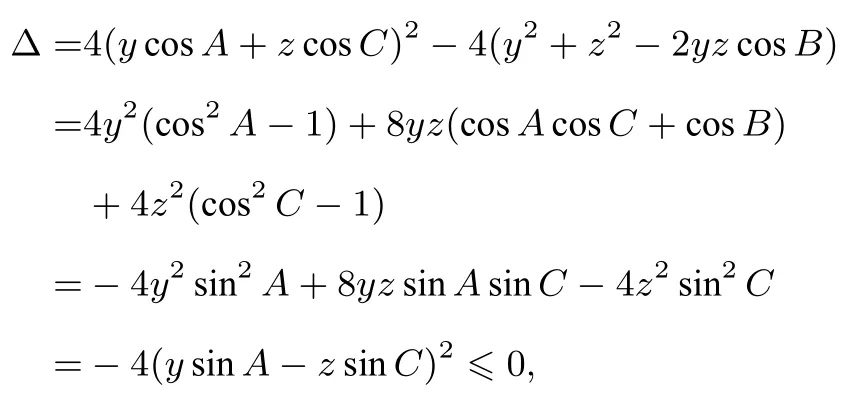
所以,f(x)>0恒成立,原不等式得证.
3.Oppenheim不等式
若三个实数A,B,C使不等式
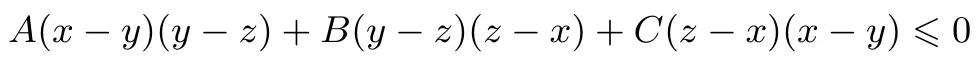
对一切实数x,y,z均成立,求证:A,B,C>0且
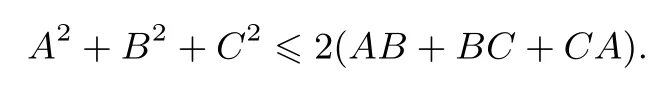
证明令x=z,则A(z−y)2>0恒成立,所以A>0.同理可得B>0,C>0.当xz时,令m=x−y,n=x−z,则m−n=z−y,则原不等式即为
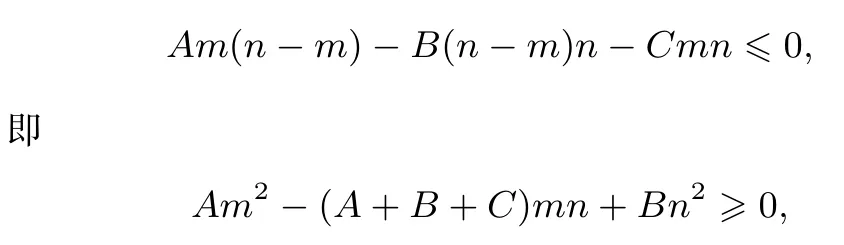
两端同时除以n2,得
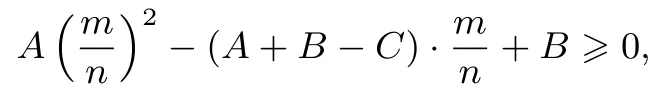
(1)当A=0时,有B=C>0,此时,显然A2+B2+C26 2(AB+BC+CA)成立;
(2)当A>0时,有判别式∆=(A+B+C)2−4AB 6 0,即A2+B2+C26 2(AB+BC+CA)成立.
4.Aczel不等式
设 a1,a2,···,an,b1,b2,···,bn为两组实数,并且则
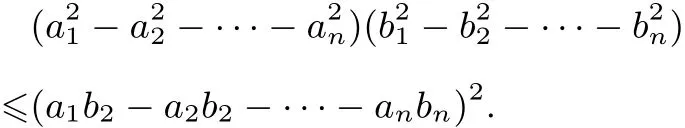
证明不妨设构造二次函数
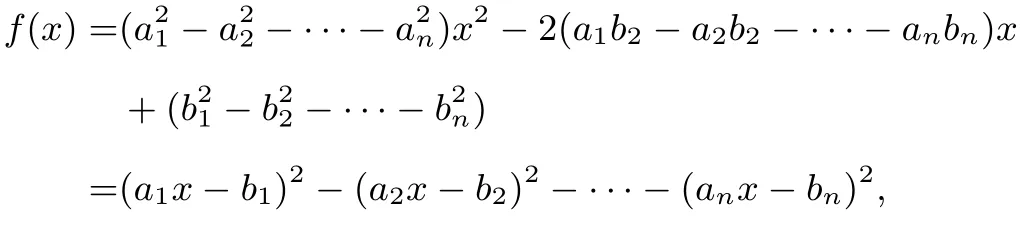
因为二次函数f(x)开口向上,且
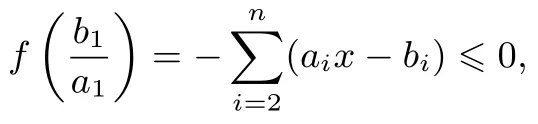
所以判别式
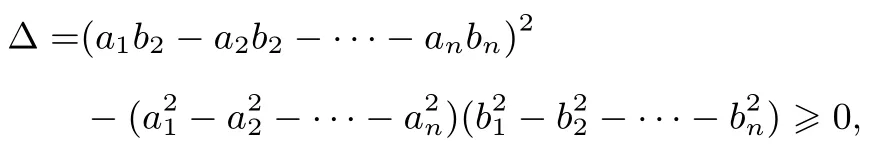
5.Polya-Szego不等式
设0 证明原不等式等价于 构造二次函数 因为二次函数f(x)开口向上,且 又因为0 即原不等式得证. 综上观之,利用判别式法证明的关键是,构造了必有实根的二次函数f(x)或取值恒非负且其二次项系数为正的二次函数f(x),具体依据为: (1)若二次函数f(x)=ax2+bx+c=0有实根,则其判别式∆=b2−4ac>0; (2)对于二次函f(x)=ax2+bx+c=0数,若a>0,则“f(x)6 0恒成立”等价于“∆=b2−4ac 6 0”. 这种证明显得直观、简捷、巧妙.值得我们不断去尝试实践.
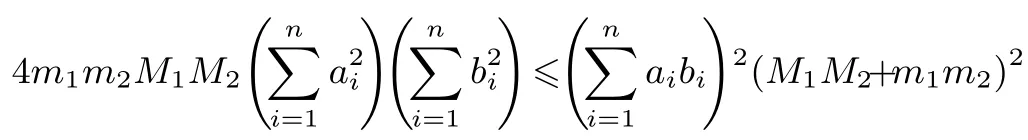
6.Beesack不等式
