源于解题的反思与联想 衍生两个有用等式

广东省韶关市曲仁中学(512040) 何世洪

源于解题的反思与联想 衍生两个有用等式

广东省韶关市曲仁中学(512040) 何世洪

一、题目

在高三数学复习课中,有这样一道题:在△ABC中,角A,B,C所对边为a,b,c.

(1)若cotA,cotB,cotC成等差数列,求证:a2,b2,c2成等差数列.

(2)已知 B=45◦,C=60◦,a=10√2,求 △ABC的面积和周长.

本题涉及一边其两夹角,面积,周长等之间的关系,利用正弦定理,余弦定理进行边角转化,有一定的计算量和综合性.该题有多种常规解法,以下是其中的一种:

(1)证明 因为cotA,cotB,cotC成等差数列,所以cotA+cotC=2cotB,即

二、反思与联想

笔者仔细推敲和反思上述解题中的式子变换,进一步剖析它们间的关系,对有关公式进行变式和联想,获得了意外的收获.如在证题过程中的变形:

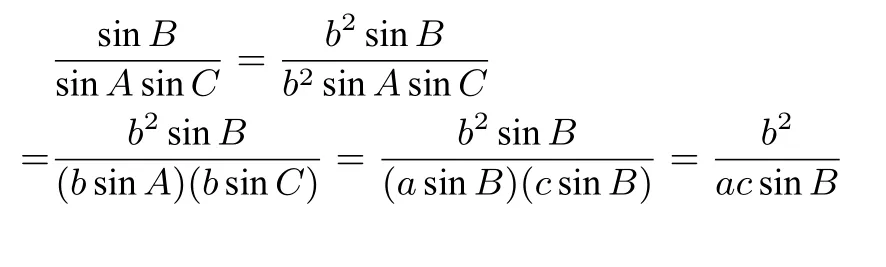
三、两个恒等式

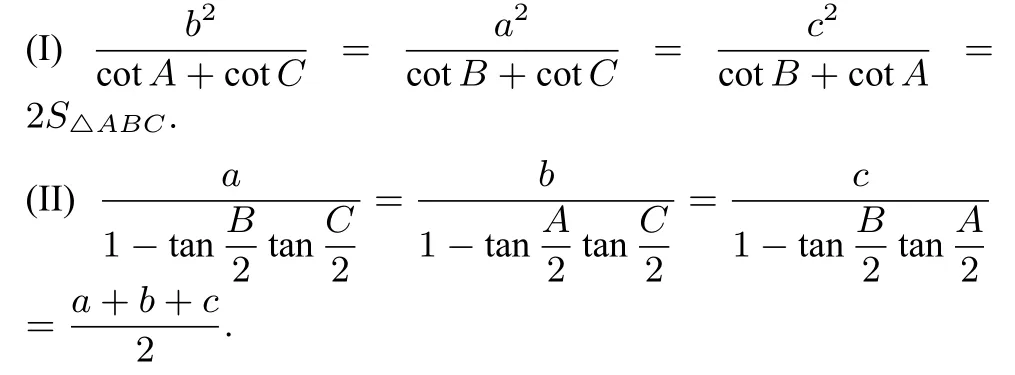
四、妙用

涉及三角形一边及其两角的正切或余切、面积和周长有关问题,通常是切化弦进行三角恒等变换,利用正弦定理和余弦定理进行处理,考察学生的转换和计算能力,具有一定的综合性,这已成为近年来数学竞赛、数学高考命题的一个热点.但应用恒等式(I)、(II)来解,会有出其不意的妙处,现例举如下.

1.求三角函数值或角

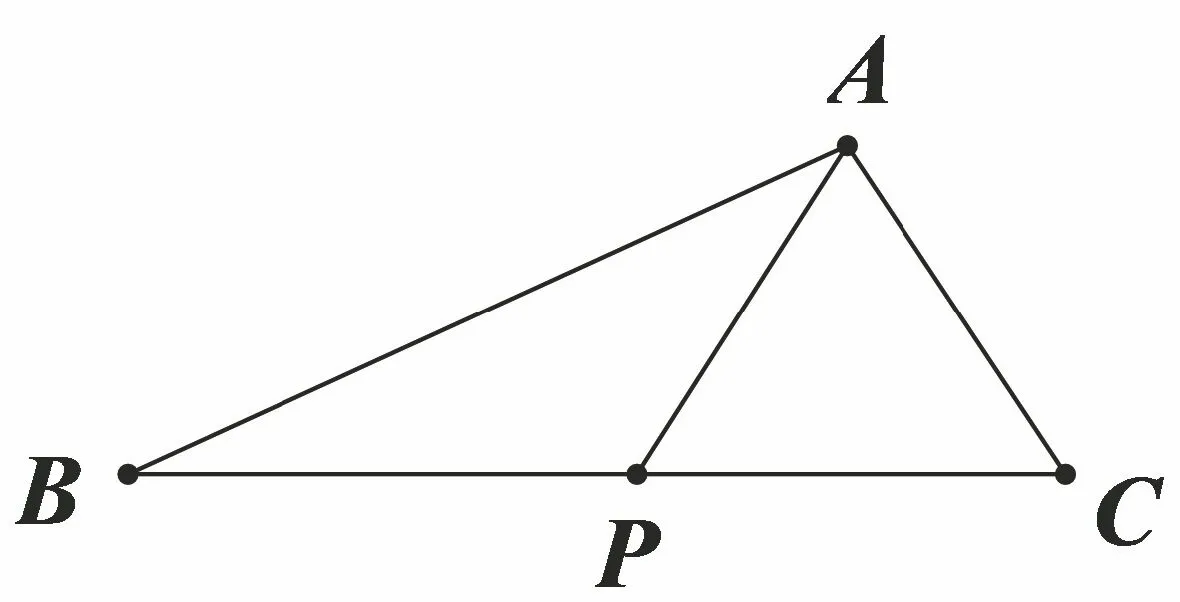
图1

例1(2017年广州普通高中毕业班综合测试(一)理科数学第17题)在△ABC中,点P在边BC 上,∠PAC=60◦,PC=2,AP+AC=4.

(1)求 ∠ACP.√

解 (1)根据等式知,在△APC中,有

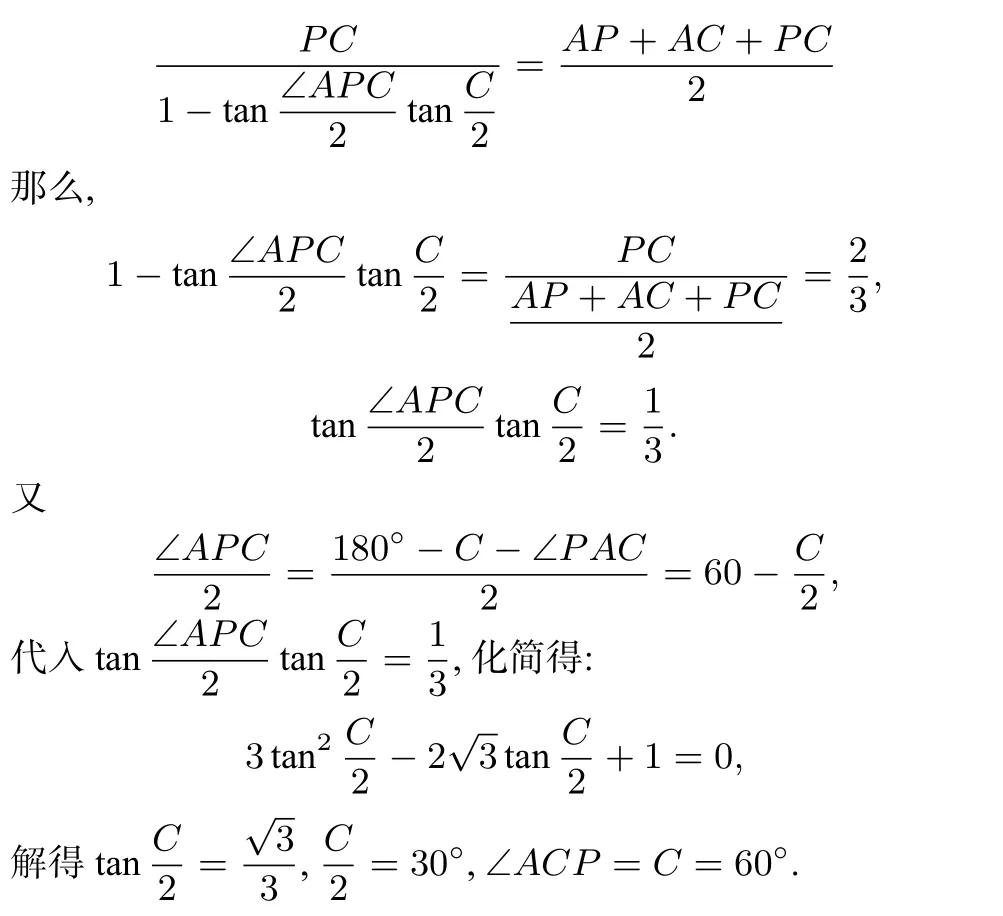
(2)由 (1)知,∠APC=60◦,△APC 为等边三角形,AP=AC=2.同样,在 △APB 中,∠APB=120◦,根据等式,有

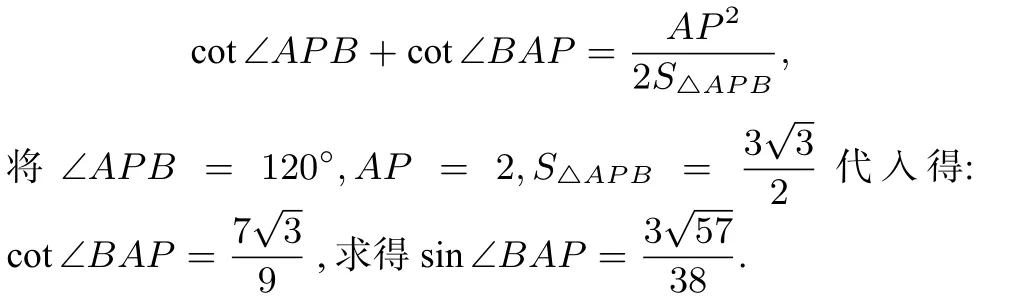
例2(1999年全国高中数学联赛)在△ABC中,角A,B,C所对边为a,b,c,若9a2+9b2−19c2=0,求的值.

解 由

例3(2004年河南省高二数学竞赛试题三(1))在非直角△ABC中,角A,B,C所对边为a,b,c,满足a+c=λb(λ>0),求证:

例4(2014年日本大学入学考题)满足∠B=2∠A和BC=1的△ABC面积最大值时,求cosB的值.

解 因∠B=2∠A,则∠C=π−3A,由

例5(安徽师大附中高三2014年1月联考数学(理科)卷)在△ABC中,角A,B,C所对边为a,b,c,若a,b,c成等差数列,求证:

证明因a,b,c成等差数列,则a+c=2b,根据等式(II),

例6 (2011年北京大学为首的11所著名高校自主招生数学试题)在△ABC中,角A,B,C所对边为a,b,c,若a+b>2c,求证:C 6 60◦.

证明由,a+b>2c,得

2.求面积或周长

(1)求角C的大小;

解(1)C=(过程略).

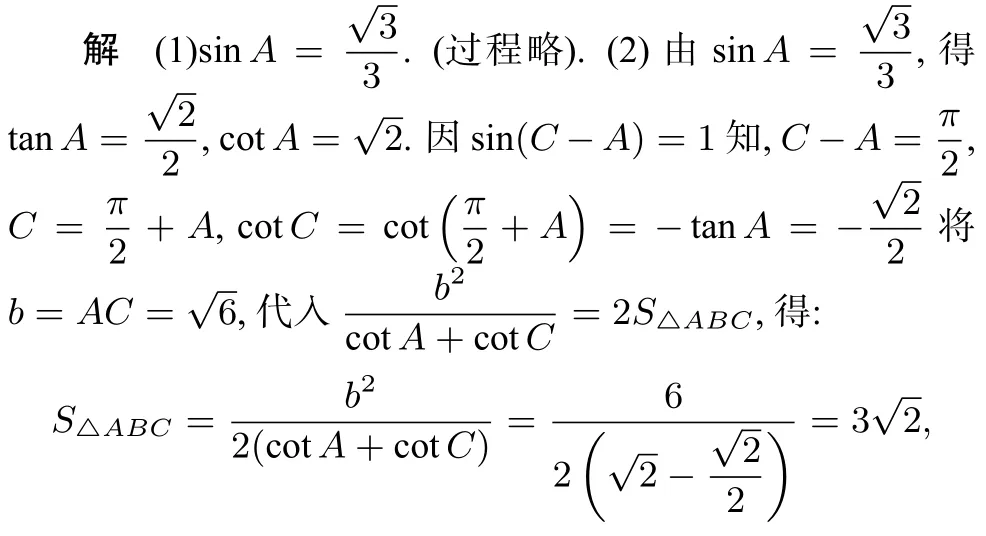
类似地,也易解2012年江西理科卷第17题:

例9 (2016年全国I卷理科17题)在△ABC中,角A,B,C所对边为a,b,c,已知2cosC(acosB+bcosA)=c,

(1)求C;

3.求边

例10(2015年浙江数学理科卷第16题)在△ABC中,角A,B,C所对边为a,b,c,已知

(1)求tanC的值;

(2)若△ABC的面积为3,求b的值.

A:直角不等腰三角形 B:等腰直角三角形

C:等腰不等边三角形 D:等边三角形

例12(2005年复旦大学自主招生考试试题)在△ABC中,tanA:tanB:tanC=1:2:3,求

在解题过程中,如果善于反思和联想,或许会获得一些源于例题但又高于例题的有价值结论,这也正体现了数学高考试题坚持“以能力立意为主”的指导思想,遵循“源于课本但又高于课本”的命题理念,从而提高我们高考的备考效率和解题能力.