爆炸波高精度数值计算程序开发及应用

徐维铮，吴卫国

1武汉理工大学高性能舰船技术教育部重点实验室，湖北武汉430063

2武汉理工大学交通学院，湖北武汉430063

爆炸波高精度数值计算程序开发及应用

徐维铮1，2，吴卫国1，2

1武汉理工大学高性能舰船技术教育部重点实验室，湖北武汉430063

2武汉理工大学交通学院，湖北武汉430063

［目的］当爆炸发生在约束空间内部，由于壁面的约束限制，爆炸冲击波的传播和演化特性将更加复杂，其对结构、内部设施及人员的损伤也更加严重。为了研究约束空间内部的爆炸特性，［方法］基于FORTRAN平台，采用三阶WENO有限差分格式，自主开发约束空间内部爆炸波高精度三维数值计算程序。利用Sod激波管、双爆轰波碰撞、空中爆炸等经典算例，验证所开发程序的可靠性。基于验证的程序，开展约束空间内部爆炸波数值计算，研究密闭空间、泄压空间及连通空间内部的爆炸波传播规律与爆炸载荷特性。［结果］研究表明，所开发的程序能较好地模拟约束空间内的爆炸过程。［结论］该开发工作可为后续研究复杂空间内部爆炸波传播路径、评估爆炸载荷以及合理设计抗爆结构奠定基础。

爆炸冲击波；约束空间；数值模拟；高精度计算程序；WENO格式；程序开发

0 引 言

随着现代反舰武器的迅速发展，各种高性能的半穿甲反舰导弹已成为水面舰船水线以上部分舷侧的主要威胁，其对舰攻击破坏特点是穿透舰船舷侧外板在舱室内发生爆炸。当爆炸发生在舱室内时，由于冲击波在传播过程中受到舱室壁面的约束限制，将产生持续时间短暂、峰值逐渐衰弱的冲击波以及持续时间较长的准静态超压［1-2］，并对舱室结构、内部设施及人员造成严重的损伤。近年来，国内外学者针对舱室、约束空间内爆炸载荷，在试验、数值模拟、高精度数值计算方法等方面开展了大量研究工作。

Edri等［3］在设置有泄压口的长方体房间内开展了TNT药柱爆炸实验，分析了装药质量对内爆炸载荷的影响规律。Wu等［4］开展了封闭空间内爆炸实验，研究了炸药形状和起爆位置对爆炸冲击波的影响规律。胡洋等［5］用压力传感器记录了长方体混凝土密闭空间内爆炸壁面上爆炸载荷的压力时间历程曲线，分析了壁面上爆炸载荷的分布规律。侯海量等［6］开展了舱室内爆炸冲击波载荷特性的实验研究。孔祥韶等［7］实验研究了角隅结构形式对舱内爆炸载荷的影响规律。侯海量等［8］基于MSC.DYTRAN软件，数值研究了舱室内爆炸冲击波的载荷特性。孔祥韶等［9］基于MSC.DYTRAN软件数值研究了舰船舱室内战斗部爆炸及爆炸毁伤效应。丁阳等［10］利用AUTODYN商用程序中的Remap技术对室内爆炸进行模拟，研究了壁面爆炸载荷的分布规律。樊壮卿等［11］基于LS-DYNA软件，数值模拟了大体积、复杂结构的典型舱室内爆炸载荷传播特性。

综上所述，当前对约束空间内部的爆炸载荷研究主要采用试验测试和商用软件数值模拟2种方法。鉴于爆炸试验昂贵且存在一定的风险，数值模拟成为研究爆炸波传播及爆炸载荷特性的主要手段。然而，包括LS-DYNA，MSC.DYTRAN和AUTODYN在内的现有商用程序的求解器主要采用传统的二阶精度算法来模拟爆炸过程，如有限差分Euler-FCT和有限体积Roe方法。这些方法因计算精度较低，会严重抹平爆炸冲击波峰值压力。准确预报爆炸载荷是合理设计和评估抗爆结构的依据，而目前发展成熟的高精度计算方法尚未集成到商用程序中，故研究和开发高精度爆炸波数值计算程序具有重要的工程意义。

对于属于高压力比、高密度比的炸药爆炸问题，其数值模拟对激波捕捉格式提出了更高的要求。为此，Liu等［12］于1994年提出了WENO格式（Weighted essentially non-oscillation scheme），Shu等［13-15］发展了该格式。WENO格式在有效性、通量的光滑性和收敛解的稳定性方面均优于ENO格式［16］，所以将WENO格式用于模拟爆炸过程是一个比较好的选择。

本文将基于FORTRAN平台，采用三阶WENO有限差分格式，自主开发舱室内的爆炸波高精度数值计算程序，利用所开发的程序研究密闭空间、泄压空间及连通空间内部的爆炸波传播规律与爆炸载荷特性。该研究工作可为后续爆炸波传播、爆炸载荷以及抗爆结构设计提供基础。

1 程序开发

1.1 欧拉方程

基于瞬时爆轰假定，将炸药等效为高压、高密度气体。爆炸流场的控制方程采用三维可压缩欧拉方程［17］进行描述：

式中，U为守恒通量；E，F，G为数值通量，并分别表示如下：

式中：ρ为密度；u，v，w分别为x，y，z方向上的速度分量；p为流体压力；E为单位体积流体的总能量；e为比内能；γ为气体的绝热指数，本文数值计算中取为1.4。

1.2 数值离散方法

采用Strang维数分裂法，将欧拉方程分解为x，y，z方向进行求解。采用三阶WENO有限差分格式对欧拉方程的空间项进行数值离散，具体离散过程如下。

单元面中心点xi+1/2处的数值通量fi+1/2为

式中：fi，fi+1分别为点xi，xi+1处的数值通量；ω0为非线性权重；D0=fi-1-fi；D1=fi-fi+1。

式（5）中的ω0由下式求得：

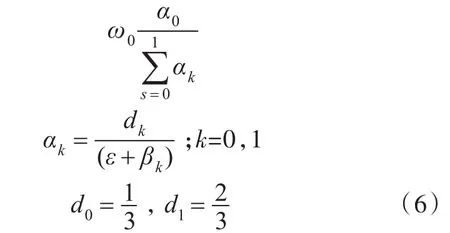
式中：ε为避免分母为零的小数，取ε=1.0×10-6；k为三阶WEND格式子模权的个数；dk为三阶WENO格式的线性权值；αk为转换函数，三阶WENO 格式的 2个子模板为{xi-1，xi}，{xi，xi+1}；βk(k=0，1)为光滑因子，其表达式如下［18］：

采用三阶TVD-RK法［19］对欧拉方程的时间项进行数值离散，具体离散格式如下：

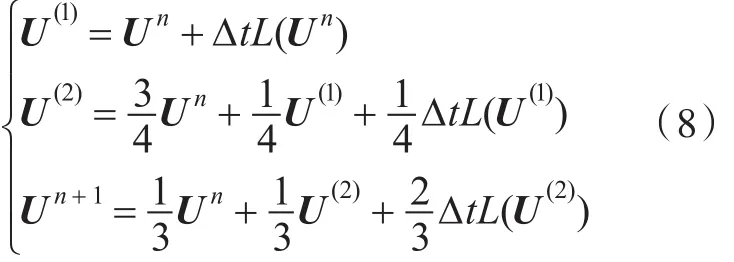
式中：Un为n时刻的守恒通量；U(1)，U(2)为中间变量；Un+1为n+1时刻的守恒通量；Δt为时间步长；L(·)表示运算算子。

2 算例验证

2.1 Sod激波管

该算例的初始条件如式（9）所示［20］，两端边界条件设置为流出边界，网格数为200个，计算结束时间为0.18。图1所示为计算结束时的无量纲压力曲线。

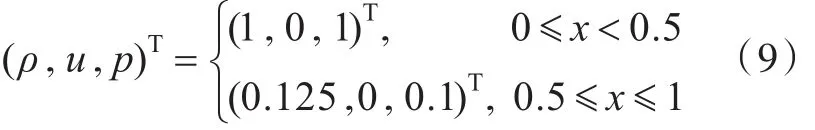
式中：ρ，u，p分别为无量纲密度、速度和压力。

2.2 双爆轰波碰撞

该算例的初始条件如式（10）所示［21］，两端边界条件设置为反射边界，网格数为800个，计算结束时间为0.038。图2所示为计算双爆轰波碰撞结束时的无量纲压力曲线。

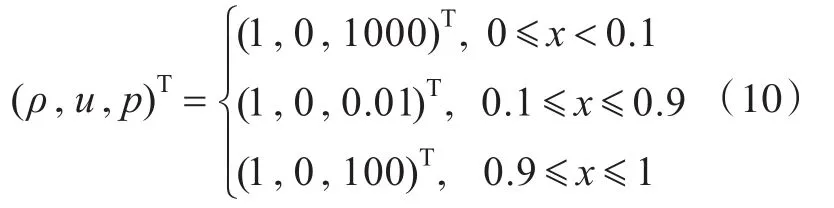
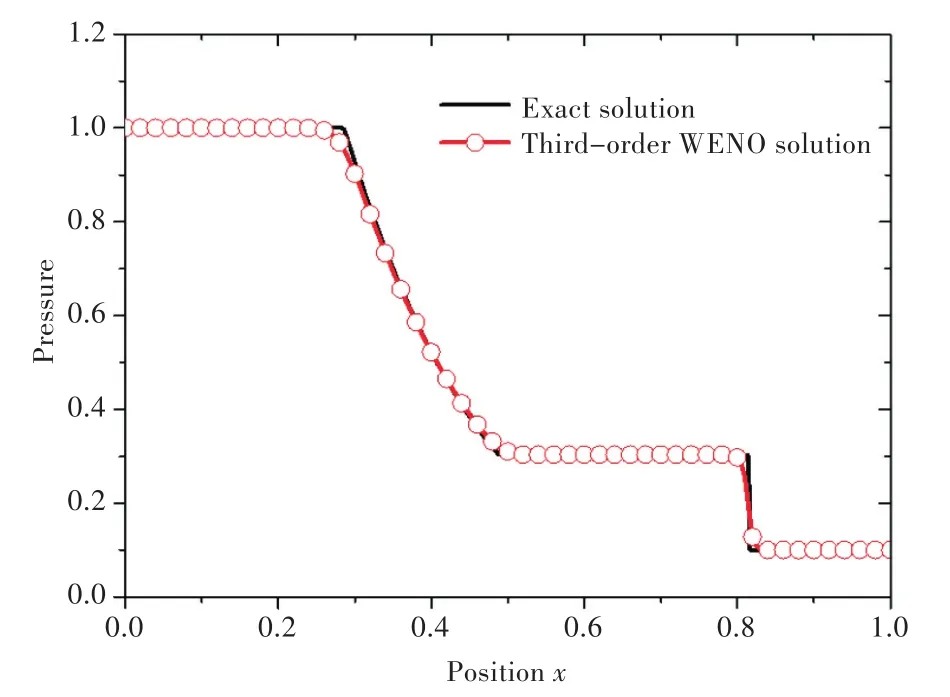
图1 Sod激波管算例计算的压力曲线Fig.1 Pressure curves calculated by the case of the sod shock tube

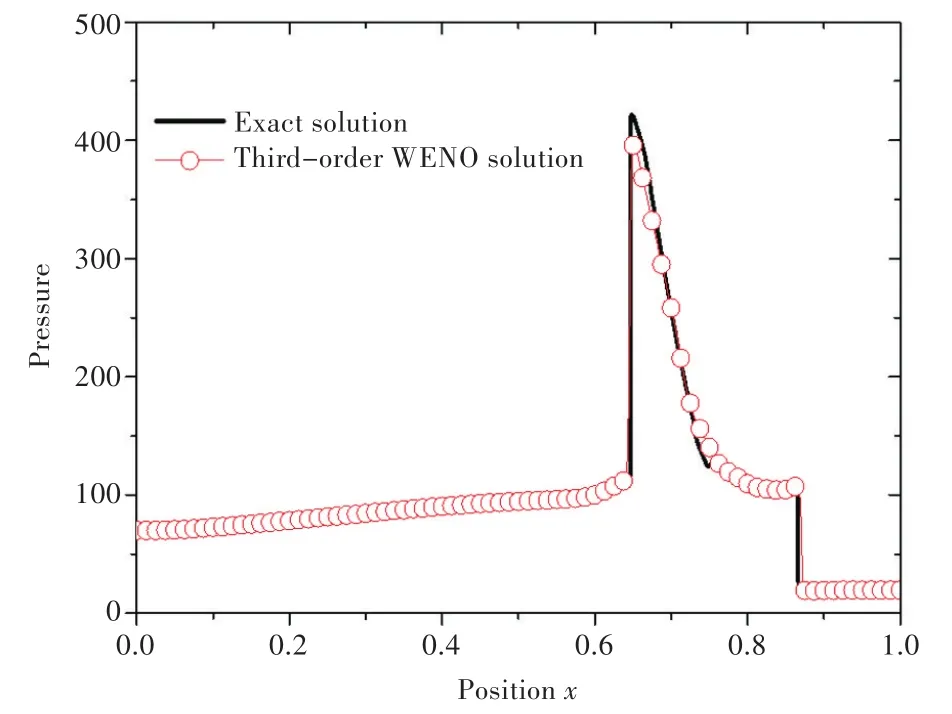
图2 双爆轰波碰撞算例计算的压力曲线Fig.2 Pressure curves calculated by the case of the interacting blast wave

2.3 空中爆炸

设计算域长度5 000mm，装药半径100mm。炸药瞬时爆轰等效后的高压、高密度气体参数如下：ρ=1 630 kg/m3，P=3.057 9×109Pa。经多次数值试验，网格尺寸取10mm。图3所示为选取典型位置（即2，3 m）的压力时间历程输出与AUTODYN商用程序输出结果的对比。

由图1、图2、图3的对比结果可知，本文所开发的数值计算程序具有较高的精度和一定的可靠性。

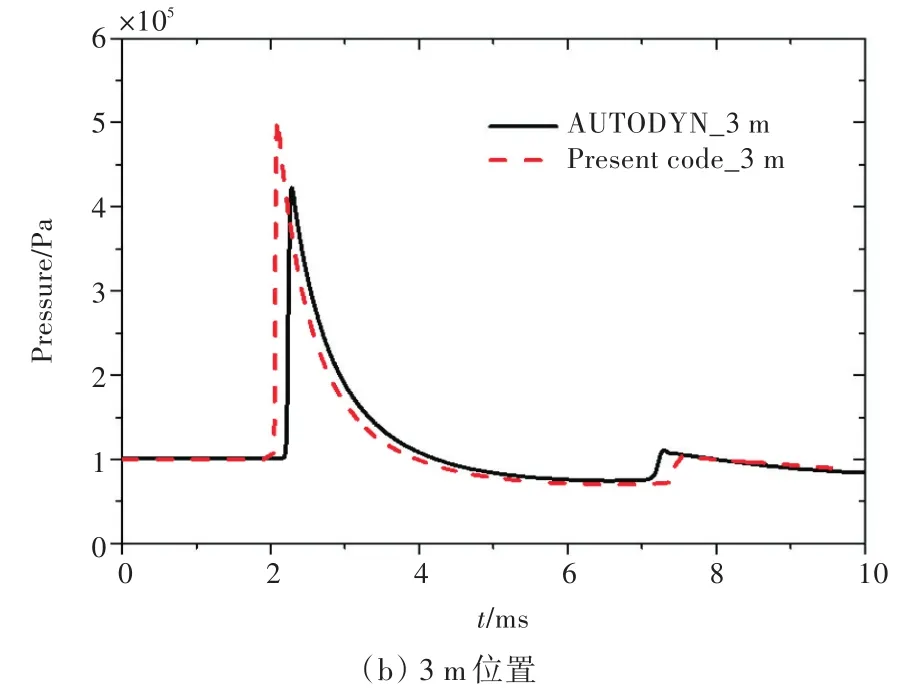
图3 典型位置处的空中爆炸压力时间历程对比Fig.3 Comparisons of pressure time history of blast in air at typical locations

3 密闭空间内爆炸

3.1 初始条件设置

设密闭空间尺寸为1 800mm×800mm×800mm，壁面设置5个测点（No.1～No.5）对爆炸超压时间历程进行输出（图4）。500 g柱形炸药放置在密闭空间中心位置，等效后的高压、高密度气体参数如下：半径 99mm，高度 80mm，ρ=203.75 kg/m3，P=3.822×108Pa。计算初始条件如图 5（a）所示，考虑到计算时间及精度的要求，经多次数值试验，网格数取14.4万个（90×40×40），如图5（b）所示。壁面边界条件设置为刚性反射边界条件，这里不考虑冲击波与结构的耦合作用。

图4 密闭空间及测点分布示意图Fig.4 Schematic diagram of closed space and arrangement of measuring points

图5 密闭空间内部的爆炸初始条件及网格分布Fig.5 Initial conditions and mesh distribution in closed space

3.2 爆炸波传播过程

图6所示为不同时刻输出时密闭空间内部的爆炸初期压力分布云图。由图6可以分析出爆炸初期爆炸波的传播过程：高压气体首先进行三维柱对称自由膨胀，当爆炸波初次到达壁面时发生正规则反射（图6（a））；由于四周壁面约束，爆炸波向密闭空间长度方向的端面传播并在两壁面交线处形成局部压力汇聚现象，且局部汇聚压力峰值沿密闭空间长度方向传播（图6（b））；当爆炸波到达密闭空间端面处时，三壁面角隅附近区域形成压力汇聚现象（图6（c）），随后两端面反射波以近似平面波的方式向密闭空间中部传播（图6（d））。

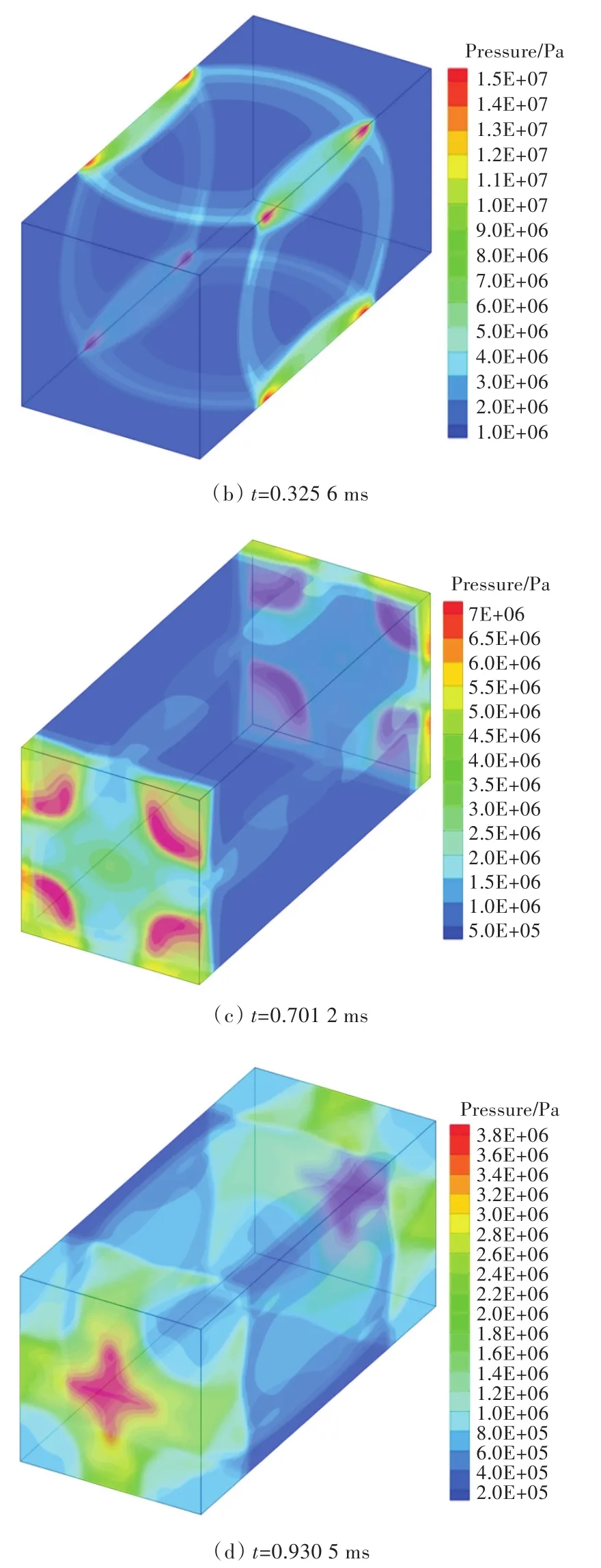
图6 密闭空间内爆炸初期压力分布云图Fig.6 Pressure distribution at early stage in closed space

3.3 爆炸载荷特性

图7所示为不同时刻输出时密闭空间内部的爆炸壁面测点超压及冲量（I）时间历程曲线。由图7（a）可知，不同测点处爆炸前期爆炸波超压峰值大小有所不同，而准静态超压峰值几乎相同（图7（a）中绿色粗实线），这说明密闭空间内部爆炸形成的准静态超压峰值在空间上是均匀的。由图7（b）可知，密闭空间内部的爆炸壁面测点冲量时间历程曲线呈现通过原点的直线分布规律，且不同测点处的差异性很小。

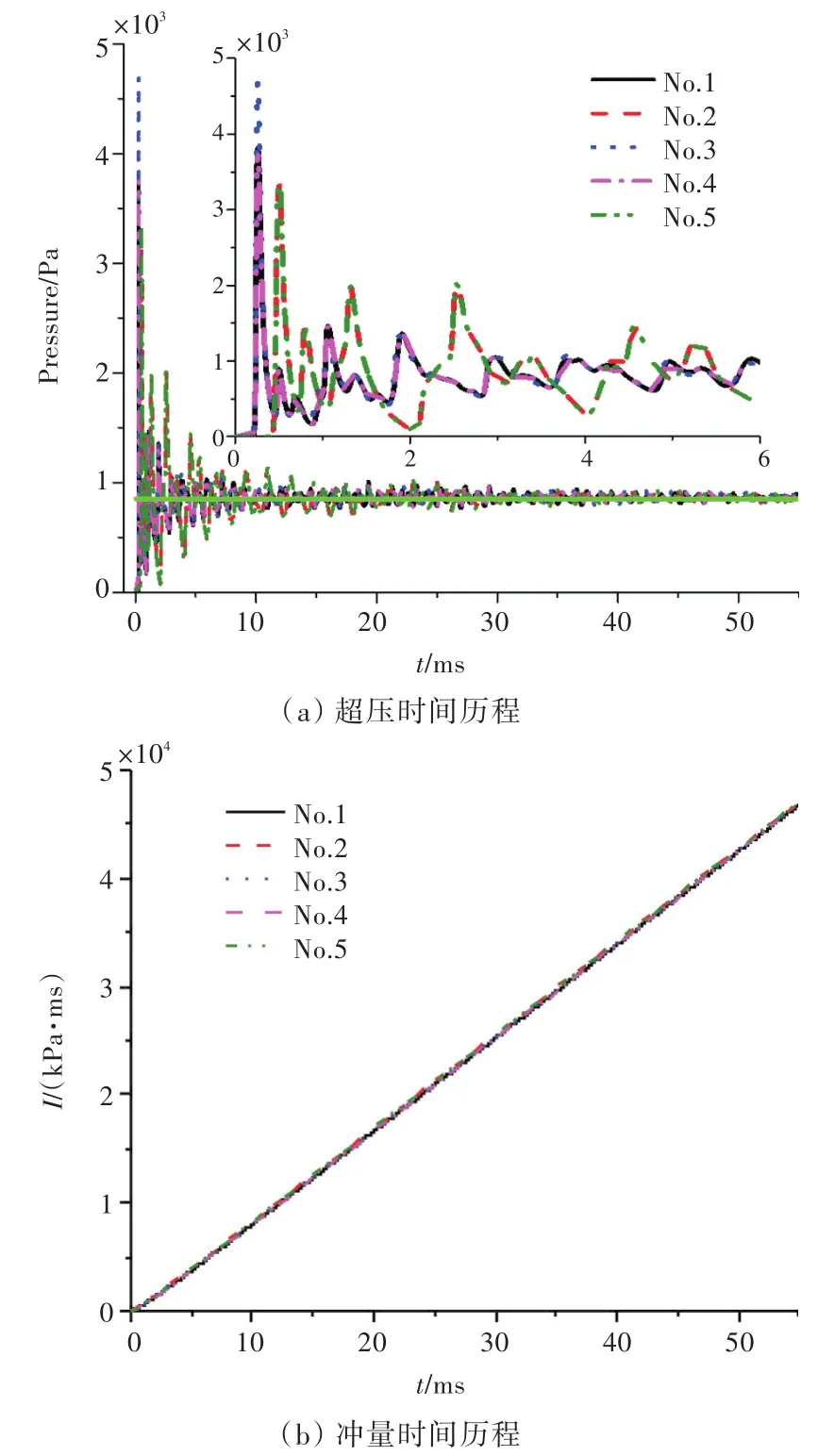
图7 密闭空间内部的爆炸载荷时间历程曲线图Fig.7 Time histories of blast load at the gauging points in closed space

4 泄压空间内爆炸

4.1 初始条件设置

泄压空间的尺寸及测点布置与第3.1节的设置相同，仅在泄压空间长度方向的某一壁面上设置了一个方形泄压口，如图8所示。方形泄压口的边长为320mm，以下图中记为L320mm。769 g柱形炸药放置在泄压空间中心位置，等效后的高压、高密度气体具体参数如下：半径100mm，高度120mm，ρ=203.75 kg/m3，p=3.822×108Pa。计算初始条件如图9所示，考虑到计算时间及精度的要求，经多次数值试验，网格数仍为14.4万个（90×40×40）。壁面边界条件设置为刚性反射边界条件，泄压口处边界条件设置为透射边界。

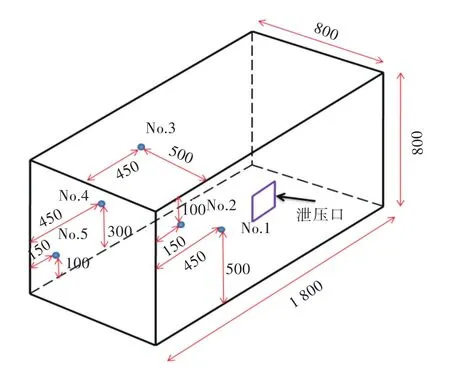
图8 泄压空间及测点分布示意图Fig.8 Schematic diagram of venting space and arrangement of measuring points

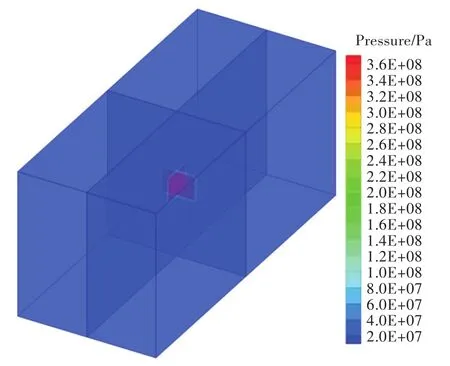
图9 泄压空间内爆炸初场Fig.9 Initial conditions in venting space

4.2 爆炸波传播过程

图10所示为不同时刻输出时泄压空间内部的爆炸初期压力分布云图。由图10可知，泄压空间与密闭空间内部爆炸波传播过程基本上是遵循相同的规律，最大差别是：由于高压气体从泄压口处泄出，使得泄压空间泄压口区域附近的压力降低（图10（a）），但这种泄压过程对爆炸初期高强度爆炸波的传播过程影响较小。

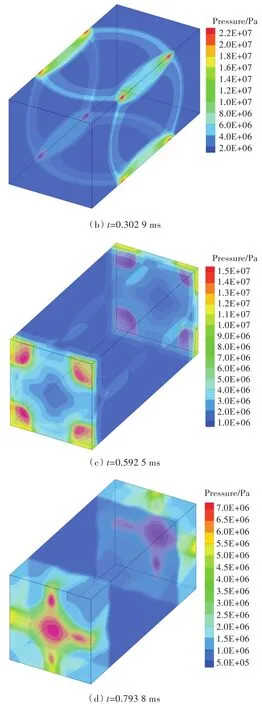
图10 泄压空间内爆炸初期压力分布云图Fig.10 Pressure distribution at early stage in venting space

4.3 爆炸载荷特性

图11所示为泄压空间内部爆炸壁面上所有测点超压及冲量时间历程曲线。由图11（a）可知，不同测点处爆炸前期爆炸波超压峰值大小有所不同，而准静态超压时间历程几乎相同（图11（a）中绿色粗实线）。这说明泄压空间内爆炸形成的准静态超压时间历程在空间上是近似均匀的。准静态超压曲线遵循指数衰减规律，与文献［22］中基于大量实验数据的假定一致。

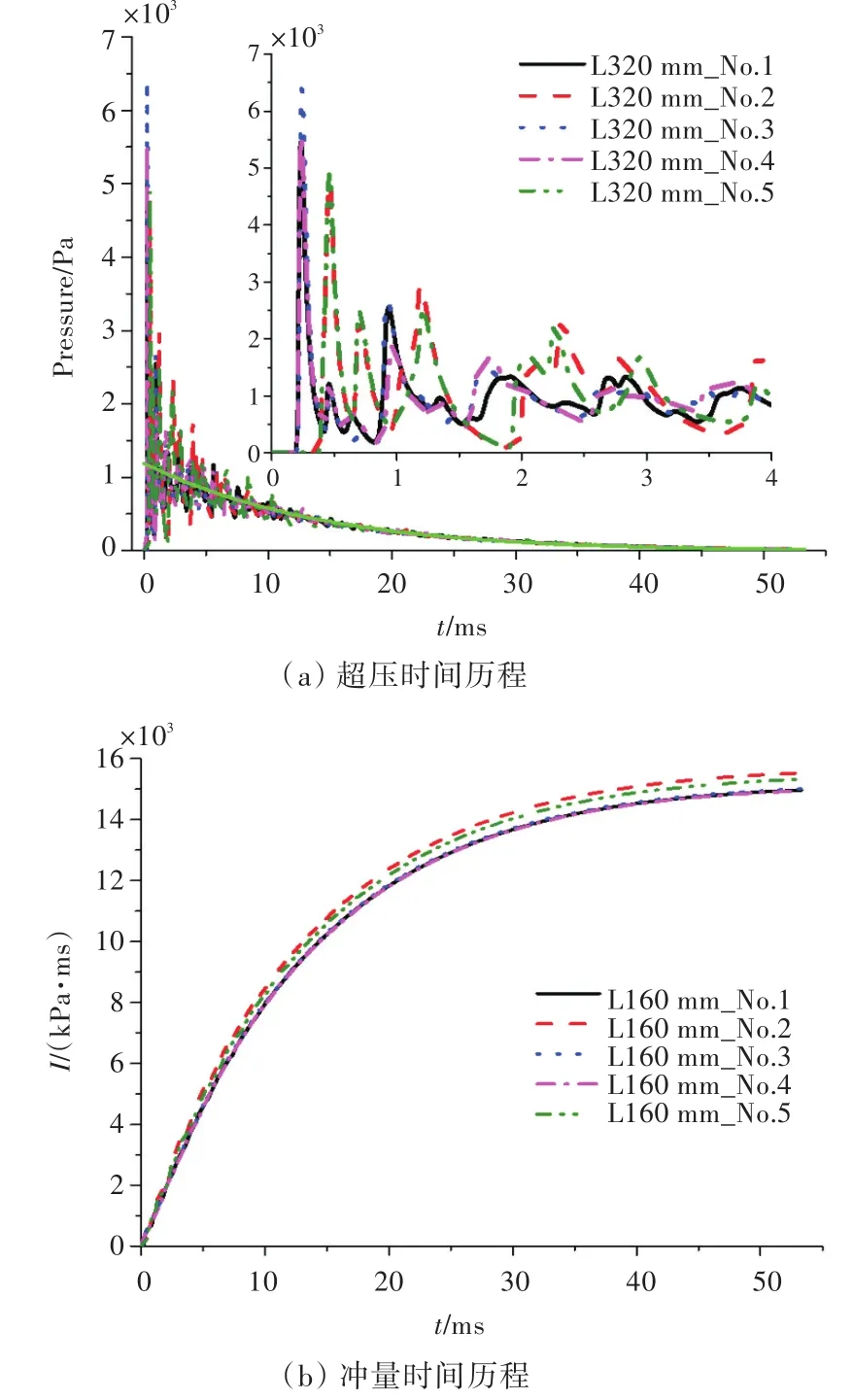
图11 泄压空间内部的爆炸载荷时间历程曲线Fig.11 Time histories of blast load at the gauging points in venting space

由图11（b）可知，泄压空间内爆炸壁面测点冲量时间历程曲线呈现通过原点的抛物线分布规律，且不同测点处存在一定的差异性。1，3，4号测点处于同一切平面1（x=1 350）内，冲量时间历程基本相同。2，5号测点处于同一切平面2（x=1 650）内，冲量时间历程基本相同。而由于切平面1相较于切平面2更靠近泄压口，使得其冲量时间历程衰减速率相对快一些。

4.4 泄压口位置的影响

本小节主要探讨泄压口位置对泄压空间内爆炸载荷的影响规律。泄压空间的尺寸与第3.1节的设置相同，但设定了3种不同的泄压口位置，如图12所示分别为：泄压空间x方向半长度平面偏左450mm、中间0mm、偏右450mm。图13所示为不同泄压口位置爆炸工况下典型测点3的超压及冲量时间历程曲线。

由图13可知，泄压口位置对泄压空间内爆炸准静态超压载荷几乎没有影响，而对冲量时间历程产生了一定的影响，缩小泄压口与炸药的相对距离能降低冲量的大小。

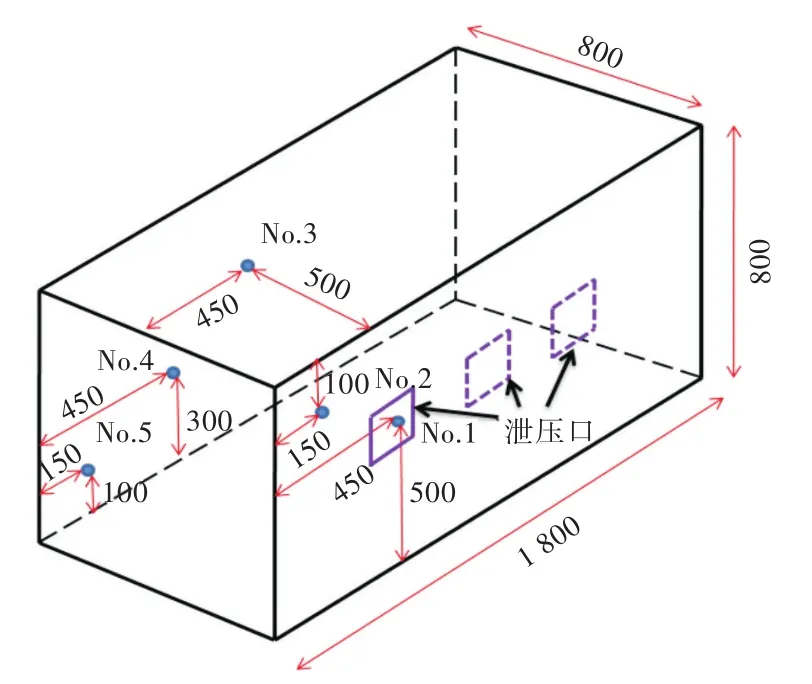
图12 泄压口位置示意图Fig.12 Schematic diagram of venting hole locations in venting space

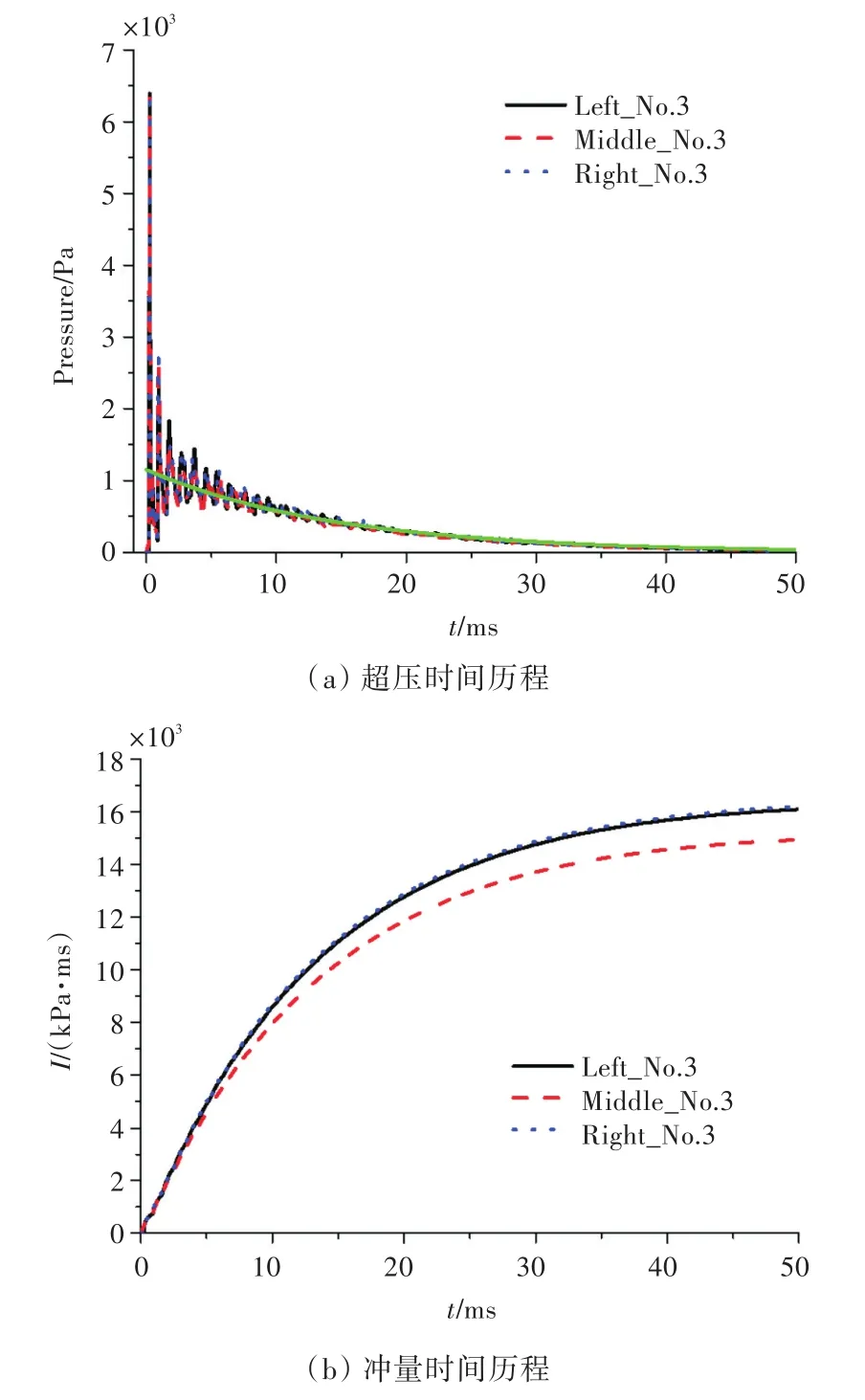
图13 不同泄压口位置测点3爆炸载荷时间历程曲线Fig.13 Time histories of blast load at gauging point 3 for different positions of venting hole

4.5 泄压口大小的影响

本小节主要探讨泄压口大小对泄压空间内爆炸载荷的影响规律。泄压空间的尺寸与第3.1节的设置相同，但设定了3种不同边长的方形泄压口，分别记为L80mm，L160mm和L320mm。图14所示为不同泄压口大小爆炸工况下典型测点3的超压时间历程曲线。

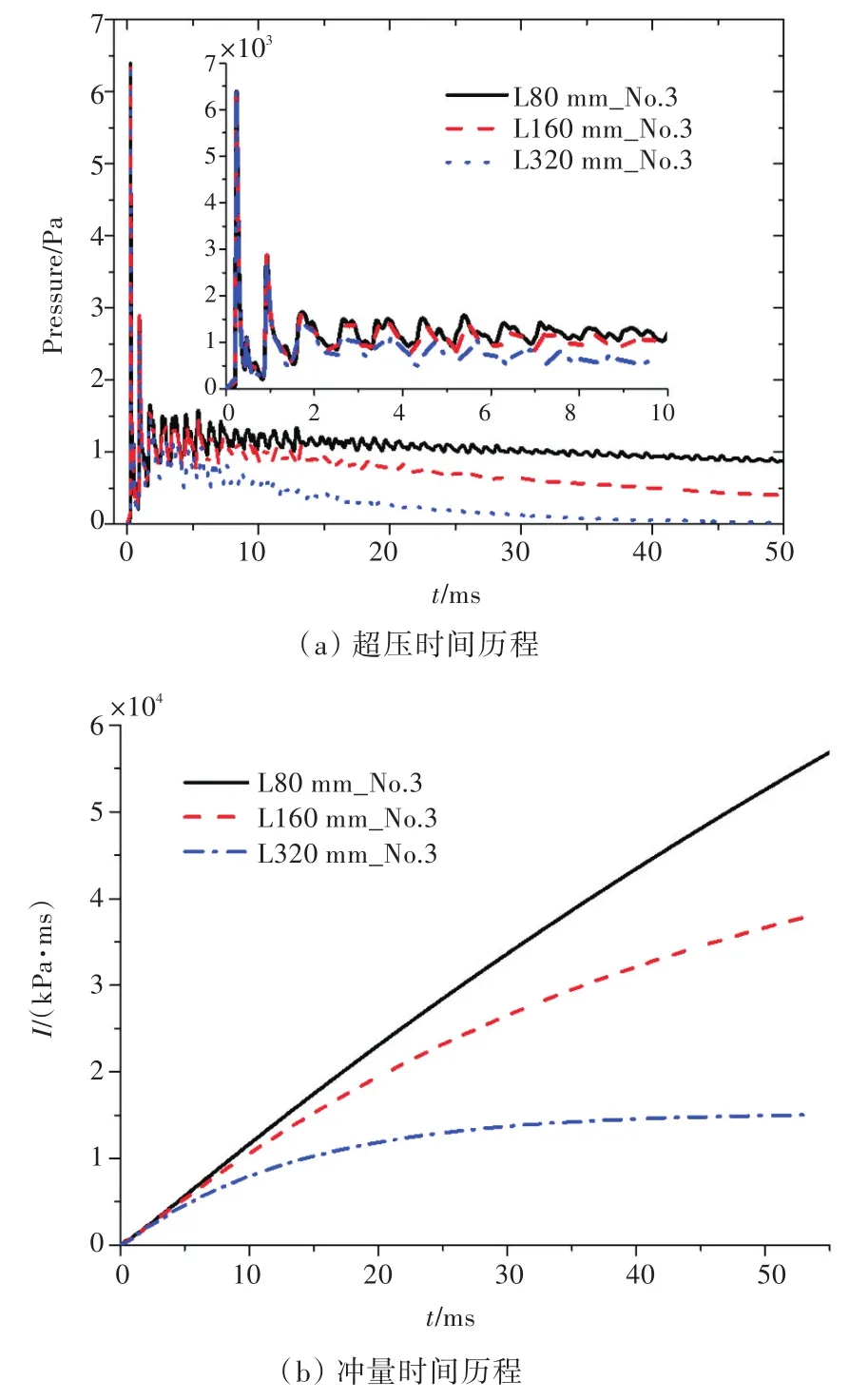
图14 不同泄压口边长测点3爆炸载荷时间历程曲线Fig.14 Time histories of blast load at point 3 for different sizes of venting holes

由图14可知：泄压口大小对泄压空间内爆炸准静态超压时间历程影响显著，泄压口边长越大，准静态超压衰减越快（图14（a））；泄压口大小对泄压空间内爆炸冲量时间历程影响显著，增大泄压口大小能显著降低冲量大小（图14（b））。通过分析可知，这主要是由于随着泄压口边长的增大，在相同爆炸波强度条件下，单位时间内从泄压口处泄出的能量越多。

5 连通空间内爆炸

5.1 初始条件设置

连通空间由左、右2个尺寸相同的约束空间和中间方形连接导管组成，连接导管截面边长为400mm。壁面上设置4个测点（No.1～No.4）对爆炸超压时间历程进行输出，如图15所示。769 g柱形炸药位于左约束空间内部，等效后的具体参数同第4.1节。计算初始条件如图16（a）所示。在计算过程中，采取正交规则网格，考虑计算时间及精度的要求，经多次数值试验，单个网格尺寸为20mm×20mm×20mm，如图16（b）所示。壁面边界条件设置为刚性壁面反射边界。

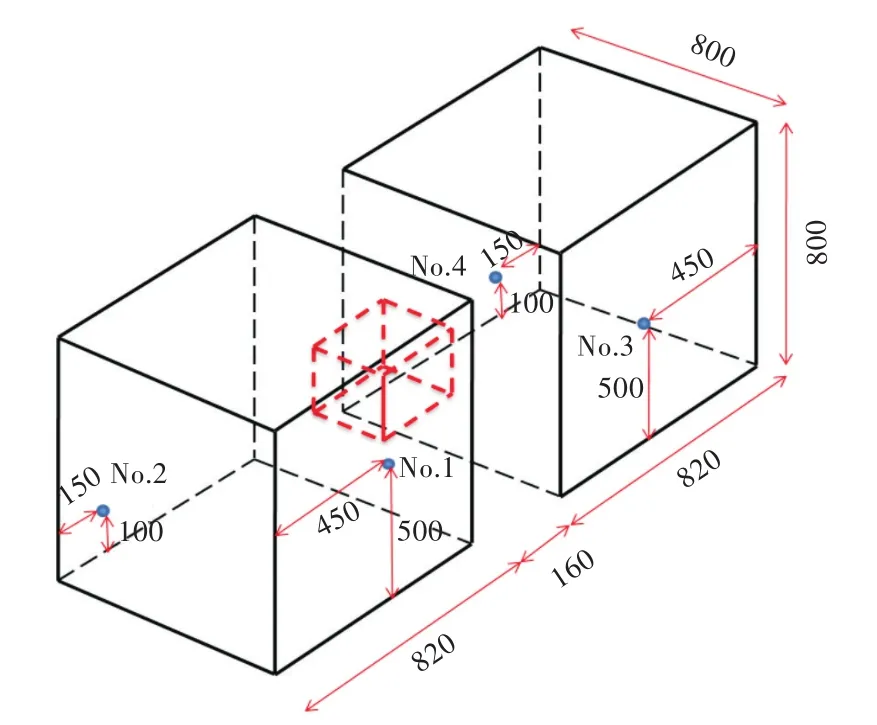
图15 连通空间及测点分布示意图Fig.15 Schematic diagram of connected space and arrangement of measuring points

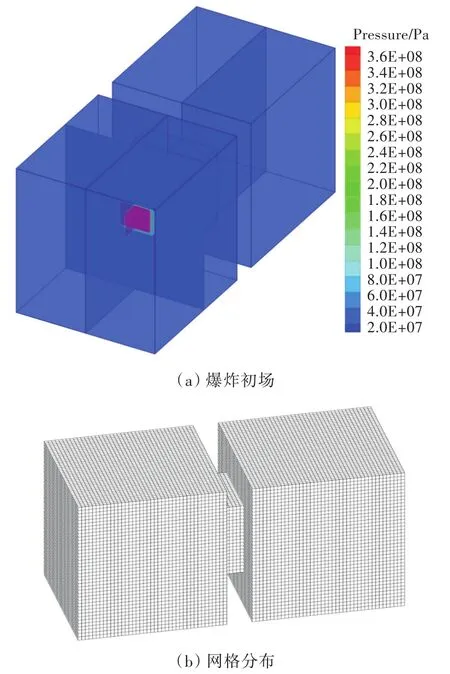
图16 连通空间内爆炸初始条件及网格分布Fig.16 Initial condition and mesh distribution in connected space

5.2 爆炸波传播过程

图17所示为连通空间内爆炸初期压力分布云图。由图17可以分析出爆炸初期爆炸波的传播过程：高压气体首先进行三维柱对称自由膨胀，爆炸波初次到达壁面时发生正规则反射，部分高压气体从泄压导管处泄出到右约束空间，使得泄压导管区域附近的压力降低（图17（a））；由于四周壁面约束，爆炸波在左约束空间角隅附近区域开始形成压力汇聚现象（图17（b））；爆炸波通过泄压导管传播到右约束空间内部，并在右约束空间内部沿长度方向传播（图17（c））；爆炸波到达右约束空间长度方向端面后进行反射，并在右约束空间角隅附近区域形成压力汇聚现象，左约束空间内部由于爆炸波的多次反射在角隅处形成压力汇聚现象（图17（d））。

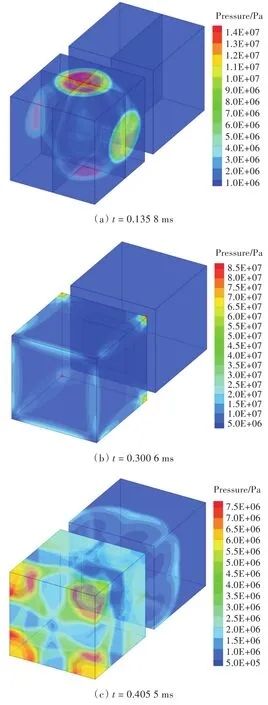
图17 连通空间内爆炸初期压力分布云图Fig.17 Pressure distribution at early stage in connected space

5.3 爆炸载荷特性

图18分别给出了左约束空间（爆炸空间）内爆炸壁面测点1，2的超压及冲量时间历程曲线。由图18可知，左约束空间内爆炸载荷特征与3.3小节密闭空间内爆炸具有相同的特征：不同测点具有几乎相同的准静态超压峰值及冲量时间历程。

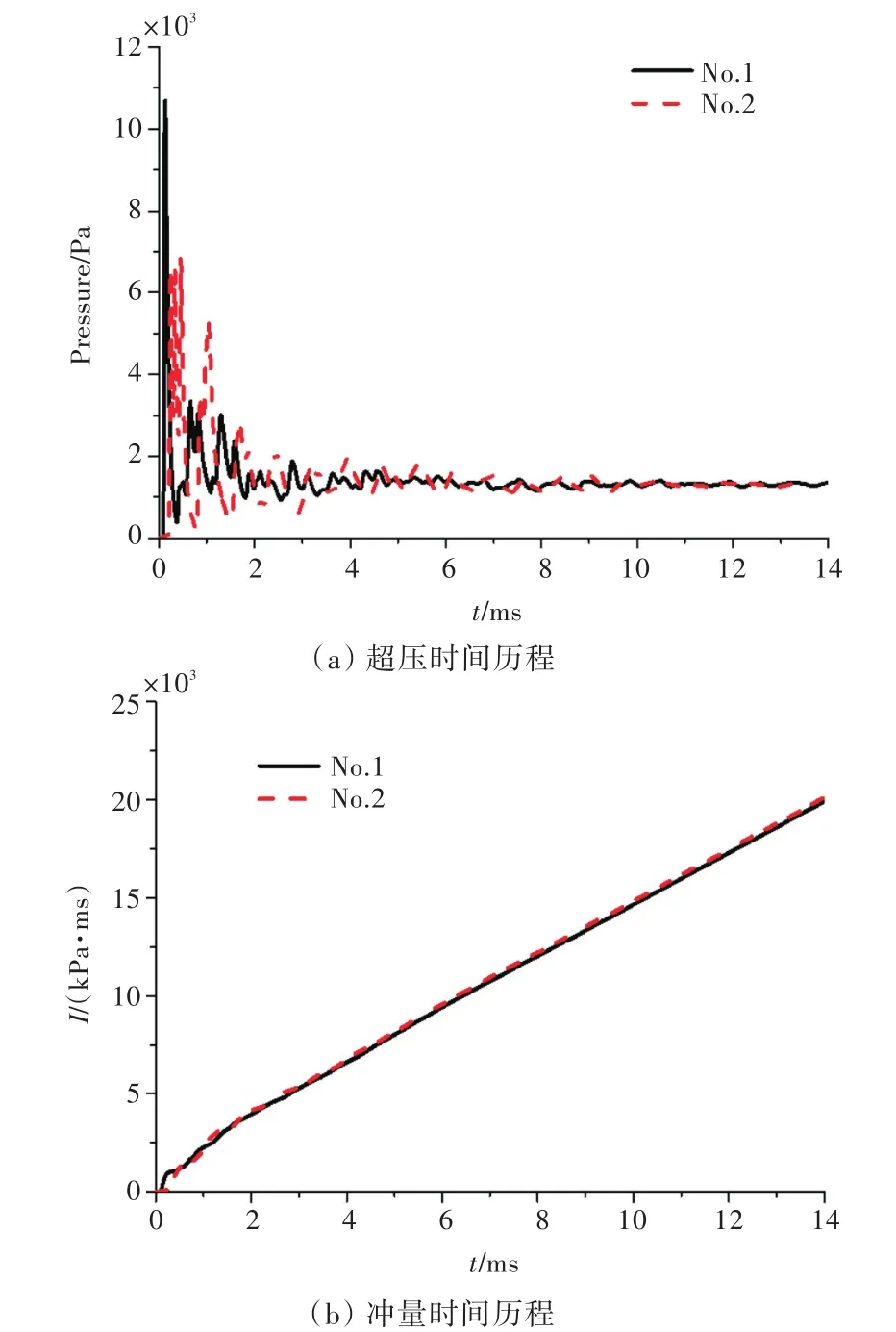
图18 左约束空间内爆炸壁面测点1，2爆炸载荷时间历程曲线Fig.18 Time histories of blast load at gauging point 1 and 2 in the left confined space

图19分别给出了右约束空间（容爆空间）内爆炸壁面测点3，4的超压及冲量时间历程曲线。由图19可知，右约束空间内爆炸载荷特征与3.3小节密闭空间内爆炸具有一个相同的特征：不同测点具有几乎相同的准静态超压峰值，而不同测点处的冲量时间历程却具有一定的差异性。

图19 右约束空间内爆炸壁面测点爆炸载荷时间历程曲线Fig.19 Time histories of blast load at gauging point 3，4 in the right confined space

图20所示为连通空间内爆炸壁面上所有测点超压时间历程曲线。由图20（a）可知，壁面不同测点位置处爆炸前期爆炸波超压峰值大小有所不同，而准静态超压峰值几乎相同（图20（a）中绿色粗实线）。这说明连通空间内爆炸形成的准静态超压峰值在空间上是均匀的，这一特征类似于密闭空间内爆炸。然而，不同测点的冲量时间历程存在较大的差异性，左约束空间内部测点的冲量明显高于右约束空间内部测点的冲量（图20（b））。分析发现，这主要是由于爆炸发生在左约束空间，较多的能量集中在左约束空间。

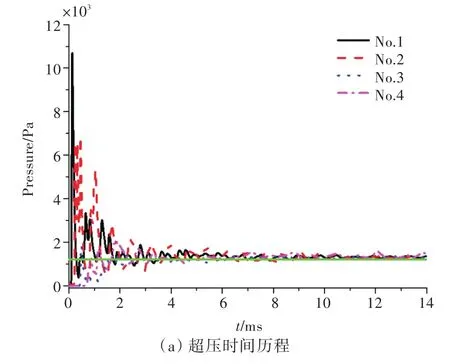
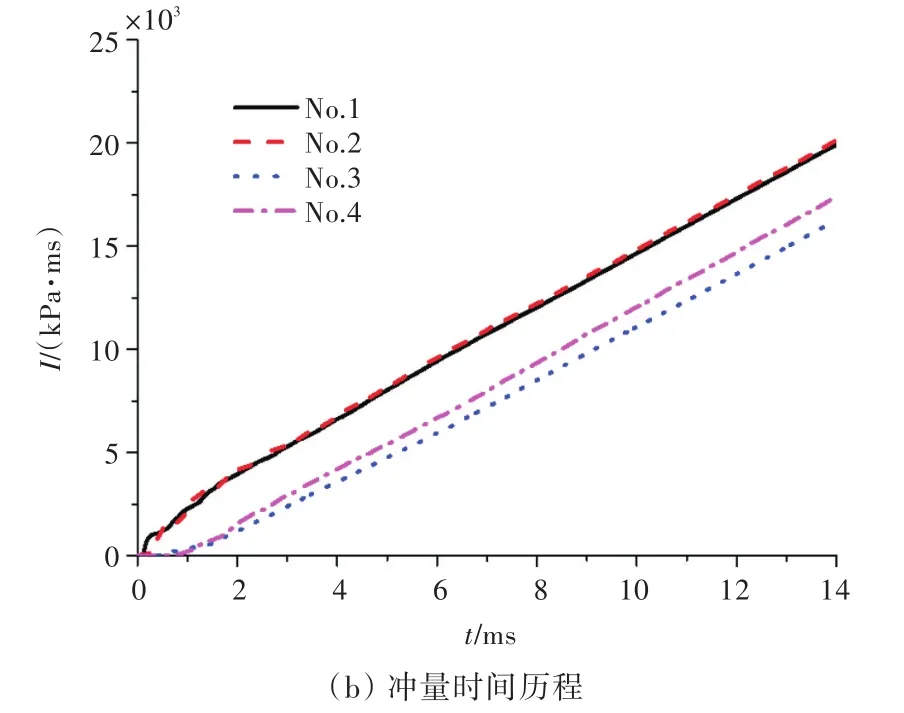
图20 连通空间内爆炸壁面测点爆炸载荷时间历程曲线Fig.20 Time histories of blast load at the gauging points in connected space

6 结 论

本文基于FORTRAN平台，采用了三阶WENO有限差分格式，自主开发了约束空间内部的爆炸波高精度数值计算程序，并开展了密闭空间、泄压空间和连通空间内部的爆炸波数值计算，分析了约束空间内部的爆炸波传播路径及爆炸载荷特性，通过研究主要得到如下结论：

1）密闭空间内部的爆炸冲量时间历程曲线呈现直线分布规律，泄压空间内部的爆炸冲量时间历程曲线呈现抛物线分布规律。

2）泄压口位置对泄压空间内部的爆炸准静态超压载荷几乎无影响，而对冲量时间历程则具有一定的影响，缩小泄压口与炸药的相对距离可降低冲量的大小；泄压口大小对泄压空间内部的爆炸载荷影响显著，增大泄压口大小可显著加快准静态压力衰减速率，降低冲量大小。

3）测点位置对连通空间内部的爆炸准静态超压载荷几乎无影响，而对冲量时间历程的影响则较显著，炸药所在约束空间的内部冲量明显高于爆炸波泄入空间的内部冲量。

［1］ESPARZA E D，BAKER W E，OLDHAM G A.Blast pressures inside and outside suppressive structures：ADA025504［R］.San Antonio，TX：Southwest Re⁃search Institute，1975.

［2］KEENAN W A，TANCRETO J E.Blast environment from fully and partially vented explosions in cubicles：ADA019026［R］.［S.l.］：Department of the Army Pica⁃tinny Arsenal，1975.

［3］EDRI I，SAVIR Z，FELDGUN V R，et al.On blast pressure analysis due to a partially confined explosion：I.Experimental studies［J］.International Journal ofProtective Structures，2011，2（1）：1-20.

［4］WU C Q，LUKASZEWICZ M，SCHEBELLA K，et al.Experimental and numerical investigation of confined explosion in a blast chamber［J］.Journal of Loss Pre⁃vention in the Process Industries，2013，26（4）：737-750.

［5］胡洋，朱建芳，朱锴.长方体单腔室空腔环境内爆炸效应的实验研究［J］.爆炸与冲击，2016，36（3）：340-346.HU Y，ZHU J F，ZHU K.Experimental study on ex⁃plosion effect in a closed single rectangular cavity［J］.Explosion and Shock Waves，2016，36（3）：340-346（in Chinese）.

［6］侯海量，朱锡，李伟，等.舱内爆炸冲击载荷特性实验研究［J］.船舶力学，2010，14（8）：901-907.HOU H L，ZHU X，LI W，et al.Experimental studies on characteristics of blast loading when exploded in⁃side ship cabin［J］.Journal of Ship Mechanics，2010，14（8）：901-907（in Chinese）.

［7］孔祥韶，吴卫国，李俊，等.角隅结构对舱内爆炸载荷影响的实验研究［J］.中国造船，2012，53（3）：40-50.KONG X S，WU W G，LI J，et al.Experimental re⁃search of influence of corner structure on blast loading under inner explosion［J］.Shipbuilding of China，2012，53（3）：40-50（in Chinese）.

［8］侯海量，朱锡，梅志远.舱内爆炸载荷及舱室板架结构的失效模式分析［J］.爆炸与冲击，2007，27（2）：151-158.HOU H L，ZHU X，MEI Z Y.Study on the blast load and failure mode of ship structure subject to internal explosion［J］.Explosion and Shock Waves，2007，27（2）：151-158（in Chinese）.

［9］孔祥韶，吴卫国，李晓彬，等.舰船舱室内部爆炸的数值模拟研究［J］.中国舰船研究，2009，4（4）：7-11.KONG X S，WU W G，LI X B，et al.Numerical simu⁃lation of cabin structure under inner explosion［J］.Chi⁃nese Journal of Ship Research，2009，4（4）：7-11（in Chinese）.

［10］丁阳，陈晔，师燕超.室内爆炸超压荷载简化模型［J］.工程力学，2015，32（3）：119-125，133.DING Y，CHEN Y，SHI Y C.Simplified model of overpressure loading caused by internal blast［J］.En⁃gineering Mechanics，2015，32（3）：119-125，133（in Chinese）.

［11］樊壮卿，王伟力，黄雪峰，等.典型舱室内爆炸仿真分析［J］.工程爆破，2015，21（3）：13-17.FAN Z Q，WANG W L，HUANG X F，et al.Simula⁃tion analysis on typical cabin internal explosion［J］.Engineering Blasting，2015，21（3）：13-17（in Chi⁃nese）.

［12］LIU X D，OSHER S，CHAN T.Weighted essentially non-oscillatory schemes［J］.Journal of Computation⁃al Physics，1994，115（1）：200-212.

［13］JIANG G S，SHU C W.Efficient implementation of weighted ENO schemes［J］.Journal of Computational Physics，1996，126（1）：202-228.

［14］SHU C W.Essentially non-oscillatory and weighted essentially non-oscillatory schemes for hyperbolic conservation laws［M］//QUARTERONI A.Advanced numericalapproximation ofnonlinearhyperbolic equations. Berlin Heidelberg： Springer， 1998：325-432.

［15］SHU C W.High order weighted essentially nonoscilla⁃tory schemes for convection dominated problems［J］.Siam Review，2009，51（1）：82-126.

［16］HARTEN A，ENGQUIST B，OSHER S，et al.Uni⁃formly high order accurate essentially non-oscillatory schemes，III［J］.Journal of Computational Physics，1987，71（2）：231-303.

［17］曹乐.利用level set方法捕捉气、水界面的三维数值研究［D］.合肥：中国科学技术大学，2009.CAO L.Three-dimensional computations on captur⁃ing of gas-water interface by level set method［D］.He⁃fei：University of Science and Technology of China，2009（in Chinese）.

［18］谢昌坦.气—水可压缩流物质界面的R-M不稳定性研究［D］.哈尔滨：哈尔滨工程大学，2011.XIE C T.The study on R-M instability of the material interface in gas-water compressible flow［D］.Har⁃bin：Harbin Engineering University，2011（in Chi⁃nese）.

［19］SHU C W，OSHER S.Efficient implementation of es⁃sentiallynon-oscillatory shock-capturingschemes［J］.Journal of Computational Physics，1988，77（2）：439-471.

［20］SOD G A.A survey of several finite difference meth⁃ods for systems of nonlinear hyperbolic conservation laws［J］.Journal of Computational Physics，1978，27（1）：1-31.

［21］WOODWARD P，COLELLA P.The numerical simu⁃lation of two-dimensional fluid flow with strong shocks［J］.Journal of Computational Physics，1984，54（1）：115-173.

［22］ANDERSON C E Jr，BAKER W E，WAUTERS D K，et al.Quasi-static pressure，duration，and im⁃pulse for explosions（e.g.HE）in structures［J］.Inter⁃national Journal of Mechanical Sciences，1983，25（6）：455-464.

Development of in-house high-resolution hydrocode for assessment of blast waves and its application

XU Weizheng1，2，WU Weiguo1，2
1 Key Laboratory of High Performance Ship Technology of Ministry of Education，Wuhan University of Technology，Wuhan 430063，China
2 School of Transportation，Wuhan University of Technology，Wuhan 430063，China

The propagation and evolution characteristics of blast waves in confined spaces are complicated due to the constraint of the surrounding walls,by which the enhanced reflected shock waves will cause more serious damage to the internal structures,facilities and personnel.In order to investigate the characteristics of explosions in confined spaces,an in-house high-resolution hydrocode was developed in this present work.The third-order WENO finite difference scheme(weighted essentially non-oscillation scheme)was implemented in the code to capture the shock waves generated by cylindrical explosives.The Sod shock tube problem,interacting blast wave problem and blast in air problem were simulated to validate the code.The validated code was then used to simulate the blast waves generated by condensed explosives in closed,vented and connected spaces.The propagation of blast waves and the characteristics of blast load were subsequently investigated.The developed code appears to accurately predict the process of explosions in confined spaces.This high-resolution hydrocode can be used to study the propagation paths of blast waves in complicated spaces and evaluate the internal blast load,which can provide reliable input for the design of explosion-resistant structures.

explosive shock wave；confined space；numerical simulation；high-resolution hydrocode；WENO scheme；program development

U661.4

：ADOI：10.3969/j.issn.1673-3185.2017.03.010

http://kns.cnki.net/kcms/detail/42.1755.TJ.20170512.1251.022.html期刊网址：www.ship-research.com

徐维铮，吴卫国.爆炸波高精度数值计算程序开发及应用［J］.中国舰船研究，2017，12（3）：64-74.

XU W Z，WU W G.Development of in-house high-resolution hydrocode for assessment of blast waves and its application［J］.Chinese Journal of Ship Research，2017，12（3）：64-74.

2016-11-28< class="emphasis_bold">网络出版时间

时间：2017-5-12 12:51

国家部委基金资助项目；国家自然科学基金资助项目（51409202）

徐维铮，男，1991年生，博士生。研究方向：爆炸波高精度数值计算方法及三维程序开发。E-mail：xuweizheng@whut.edu.cn

吴卫国（通信作者），男，1960年生，教授，博士生导师。研究方向：结构动力学。E-mail：mailjt@163.com