基于Shannon熵和EMD算法的MEMS陀螺仪信号降噪处理

王晨钢

（苏州大学 城市轨道交通学院，江苏 苏州 215000）

基于Shannon熵和EMD算法的MEMS陀螺仪信号降噪处理

王晨钢

（苏州大学 城市轨道交通学院，江苏 苏州 215000）

MEMS陀螺仪在汽车导航、旋转检测、机器人定位等方面都有广泛应用，而信号中常带有较大的漂移噪声，这使得检测结果有较明显的偏差。对此本文提出了通过采用基于Shannon熵和EMD算法对陀螺仪信号进行去噪的方法。首先，EMD算法将非线性和非平稳的陀螺仪信号分解为频率和振幅调制的波形，然后通过Shannon熵判据区分高频噪声信号和低频陀螺仪有效信号。仿真和实验验证结果表明该方法具有很好的去噪效果。

EMD；Shannon熵；陀螺仪信号；降噪

MEMS陀螺仪由于它紧凑的外形、低成本、低功耗而被大量应用于防御、汽车、航空航天等各个领域。也正因为陀螺仪的小型化和高制作精度，导致它对于电子和机械的噪声相当敏感，输出的数据中带有较大的随机漂移，而这些漂移量是非线性、非稳定的，使得测量数据中存在较大误差。

常用的陀螺仪信号降噪[1]方法有卡尔曼滤波[2-3]、短时傅里叶变换、小波变换[4-5]等。其中，卡尔曼滤波是基于建立线性模型，然而线性模型对于非稳定、非线性漂移信号并不是很有效。短时傅里叶变换应用于频域内可以获得较高的分辨率，在时域范围分辨率则较低；小波变换虽然在时频域内分辨率较高，但是在处理信号时先确定基函数和分解尺度，那么滤波结果也将是固定尺度，这样的非自适应方法在处理漂移信号时也没有较好的成效。由于受傅里叶变换的束缚，在信号的边界还会发生频谱泄露。而EMD（Empirical Mode Decomposition，EMD）算法[6-12]不仅可以较好的分析信号的频率成分，分辨率也很高；在边界也不会发生频率混叠现象，适合处理非线性、非平稳信号。本文提出了基于Shannon熵[13-16]和EMD算法，对陀螺仪信号进行去噪处理的方法。

1 EMD算法

EMD算法能把非平稳、非线性时间序列分解成一组由序列本身决定的数据序列集，即本征模态函数（Intrinsic Mode Function，IMF）。IMF必须满足两个条件：

1）极值点和过零点数目必须相等或者至多相差一个；

2）对称性，由局部极大值点构成的包络线和局部极小值点构成的包络线的平均值为零。

这种方法本质上是通过特征时间尺度获得本征振动模式，然后由本征振动模式来分解时间序列数据。对时间序列x（t）进行EMD分解的基本步骤如下：

1）初始化：r0（t）=x（t），i=1；r0（t）=x（t），i=1；

2）计算第 i个 IMF：①初始化 h0（t）=ri（t），j=1 h0（t），j=1，②找出 hj-1（t）的所有极值点；③对 hj-1（t）的极大值和极小值点分别进行三次样条差值，形成上下包络线；④计算上下包络线的平均值mj-1（t）；⑤hj（t）=hj-1（t）-mj-1（t），hj（t）一般不满足IMF条件，为原型模态函数；⑥如果，则imfi（t） =hj（t）；否则，j=j+1，转到②；

3）ri（t）=ri-1（t）-imfi（t）；

4）若ri（t）满足继续分解的条件，则i=i+1，转到2）；否则分解结束，ri（t）是残余分量。算法最后的分解结果为：

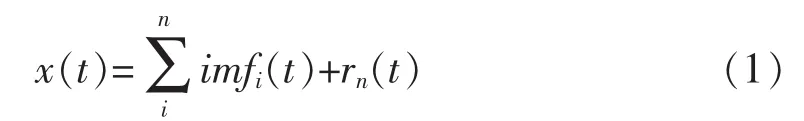
即原始时间序列经EMD分解为n个IMF和一个残余项之和。

2 基于Shannon熵的EMD算法

Shannon信息熵是对信息的量化度量方法。设一离散变量的概率分布为（p1，p2，…，pn），则Shannon熵定义为：

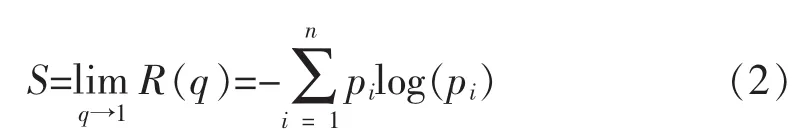
根据EMD分解的基本性质可以得到：IMF的分量中有效信号的成分会随着IMF的序号增加而增加。而前几个，尤其是第一个IMF分量，几乎完全由高频噪声构成。由此可以得出，存在某个节点js，节点左右两边的IMF分量中高频噪声和有效信号的比例的突变而造成IMF分量概率分布的突变。所以，确定这个突变点，就可以将有效信号从采样信号中分离出来。

假设采样信号为x（t），表达式如下：

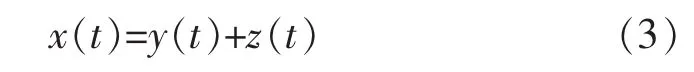
其中y（t）是纯净的原始信号，z（t）是噪声信号。

采样信号经过EMD分解之后，分成n个IMF分量和一个余项。在用IMF分量叠加还原原始信号过程中，为了减少噪声的混入，可以有选择的只叠加后几个IMF分量和余项[8]，用公式（4）来表示。

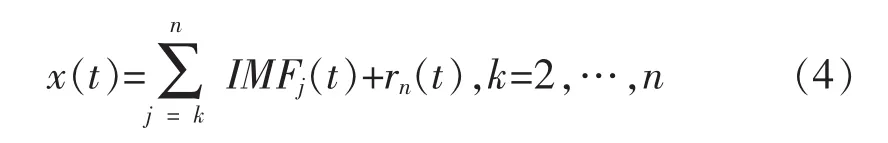
在处理过程中，使得k等于js，从而使还原出的信号尽可能的包含所有的有效信号，即还原出与原始信号最接近的信号。所以本文提出了计算Shannon熵的方法来分离噪声和有效信号。假设每个IMF的Shannon熵值为Si，i=1，…，n，可以得到相邻熵值的变换量ΔSi=Si+1-Si，i=1，…，n-1，找到最大变化量，得到js的具体数值。

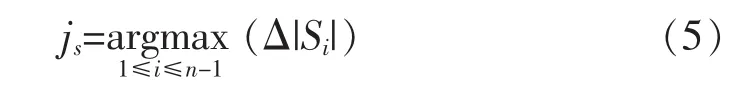
具体的滤波降噪算法如下：

1）通过EMD算法将采样信号分解为一系列IMF分量；

2）分别对每一个IMF分量计算Shannon熵Si；

3）计算相邻两个IMF分量的Shannon熵的变化量ΔSi；

4）根据步骤3），通过公式（5）确定js的取值；

5）按照js的取值，通过公式（4）对信号进行重构。

3 仿真分析

拟采用一个调频调幅非线性仿真信号进行模拟仿真分析，其表达式为

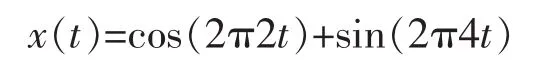
信号是分别是由频率为2Hz的余弦和频率为4 Hz的正弦信号组成，对信号添加一个信噪比为15 dB的白噪声信号n（t），将叠加后的信号作为仿真信号进行仿真实验，波形如图1所示。对叠加信号进行EMD分解，得到多个IMF分量以及一个余项，波形如图2所示。

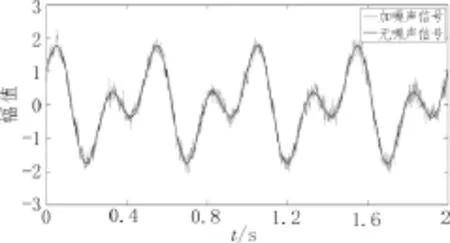
图1 无噪声信号和有噪声信号波形

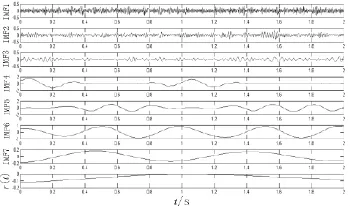
图2 EMD分解后各IMF分量波形

采用Shannon熵判据，对每个IMF分量分别进行计算，各分量值如表1所示，对应的折线图如图3。

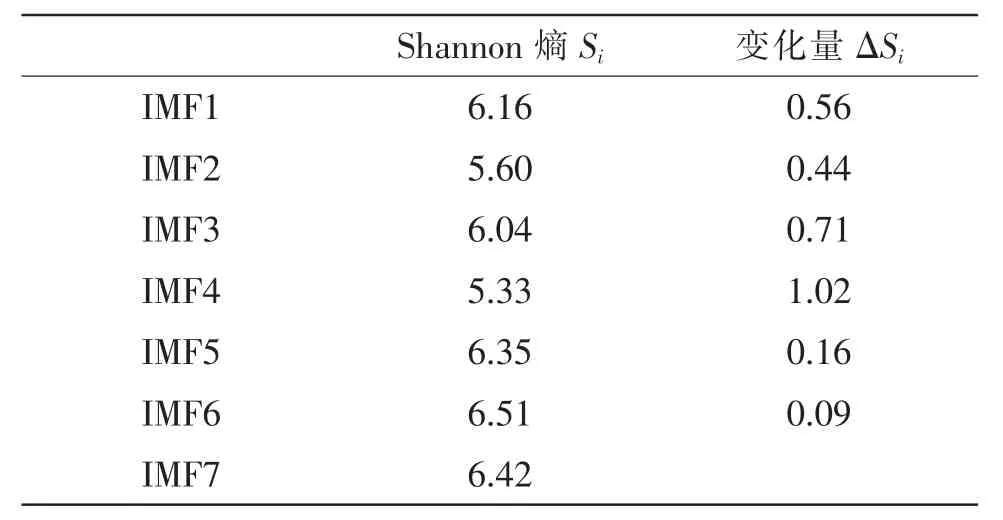
表1 各IMF分量Shannon熵值及变化量

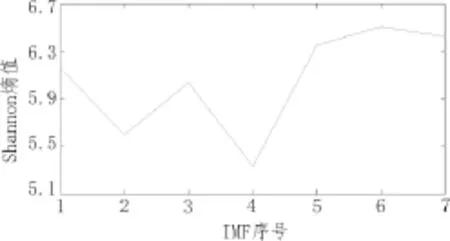
图3 各IMF分量对应的Shannon熵值折线图

从图表中可以看出，IMF4与IMF5Shannon熵的变化量ΔS4最大，并结合EMD分解的性质分析，可以得到前3个IMF分量中主要包含了高频噪声信号，后3个IMF分量中主要包含了有效信号的部分，中间一个IMF中包含着一部分的噪声和一部分的有效信号。所以可以确定，噪声与有效信号的分界点js值为4，对应的分量为IMF4。

现将后4个IMF分量与残余项γn（t）进行叠加，得到降噪后的信号，将其与无噪声信号对比，如图4。

通过计算信噪比（SNR）、均方误差（MSE）、相关系数（R）对去噪算法的效果进行量化，结果如表2。

从表2中可以看出，通过此种方法对信号进行降噪处理，信噪比和均方误差都有了明显的改善，相关系数也得到的提高。证明此种方法是有效的，可以达到降低噪声还原信号的目的。

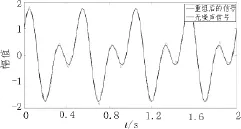
图4 重组后信号和无噪声信号波形

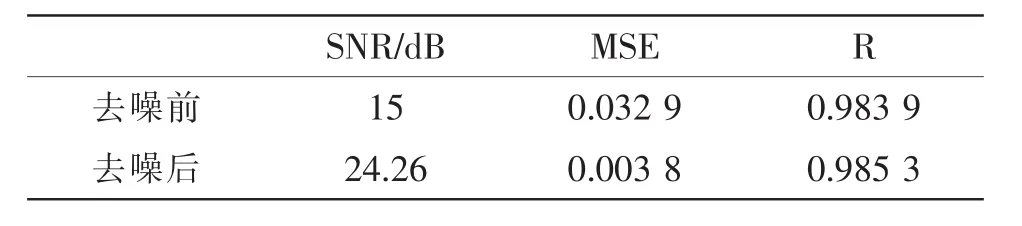
表2 降噪前后信号指标对比

4 实验验证

实验验证信号是一段德国宇航局（DLR）通信和导航研究所提供的MEMS陀螺仪的信号[17]。这段信号由安置在鞋面上的MEMS器件测量得到，记录了MEMS陀螺仪静止状态下输出的数据。信号的采样频率为100 Hz，截取10秒时间的静止信号，共1 000个采样点。使用本文中的方法对陀螺仪信号进行验证分析，结果如表3和图5所示。从图5中可以看出，静止部分的高频噪声经过去噪之后波形比较平稳，幅值接近为0。

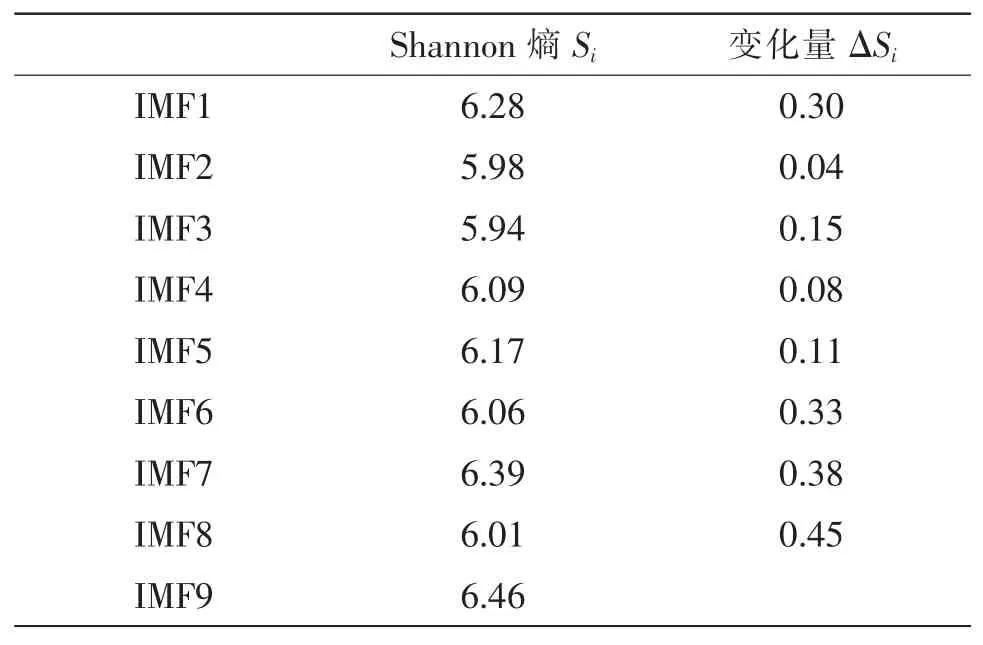
表3 各IMF分量Shannon熵值及变化量

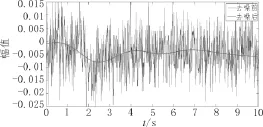
图5 基于Shannon熵和EMD算法对陀螺仪静止信号去噪前后的波形

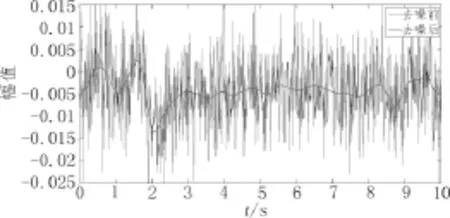
图6 小波变换对陀螺仪静止信号去噪前后的波形

对比小波变换方法，去噪结果如图6所示。可以看出，基于Shannon熵的EMD方法滤波结果比小波变换的结果更加接近真实波形（静止波形），受到噪声本身波动的影响很小。所以使用基于Shannon熵的EMD算法对陀螺仪信号进行滤波，可以有效的去除陀螺仪信号的高频噪声。

5 结束语

文中采用基于Shannon熵和EMD算法的方法对MEMS陀螺仪信号进行降噪滤波，有效的降低了陀螺仪信号中的噪声，对提高陀螺仪的精度有明显的效果。

[1]张明，曾庆军，眭翔，等.基于CEEMD的水下机器人MEMS陀螺仪降噪方法[J].传感技术学报，2014，27（12）:1622-1626.

[2]左轩尘，韩亮亮，庄杰，等.可穿戴设备中MEMS加速度计降噪方法研究 [J].压电与声光，2015，37（5）：892-895.

[3]李杰，张文栋，刘俊.基于时间序列分析的Kalman滤波方法在MEMS陀螺仪随机漂移误差补偿中的应用研究[J].传感技术报，2006，19（5）:2215-2219.

[4]吉训生，王寿荣.小波变换在MEMS陀螺仪去噪声中的应用[J].传感技术学报，2006，19（1）:150-152.

[5]牛春峰，刘世平，王中原.基于小波神经网络的MEMS陀螺输出预测方法[J].海军工程大学学报，2012，24（2）:29-32.

[6]Peel M C，G G S Pegram，T A McMahon. Empirical Mode Decomposition:Improvement and Application [J].Modsim International Congress on Modelling & Simulation Land Water & Environmental Management Integrated Systems for Sustainability，2007，364（3）:2996-3002.

[7]J.Pan，Y.Tang.Extremum Mean Empirical Mode Decomposition[J].International Congress on Image &Signal Processing，2012，57（1）:1556-1561.

[8]AO Boudraa，JC Cexus，Z Saidi.EMD-based signal noise reduction [J].Proceedings of World Academy of Science Engineering&Technology，2005，1（1）:93.

[9]AO Boudraa， JC Cexus.EMD-Based signal filtering[J].IEEE Transactions on Instrumentation &Measurement，2007，56（6）:2196-2202.

[10]Tsakalozos N，Rickard S，Drakakis K.A formal study of the nonlinearity and consistency of the Empirical Mode Decomposition [J]. Siginal Processing，2012，92（9）:1961-1969.

[11]Zhaohua Wu，Norden E.Huang.A study of the characteristics of white noise using the empirical mode decomposition method[J].Proceedings of The Royal Society.A，2004，11（2）:1597-1611.

[12]Zhen Jiang，Shihong Miao，Pei Liu.A Modified Empirical Mode Decomposition Filtering-Based Adaptive Phasor Estimation Algorithm for Removal of Exponentially Decaying DC Offset [J].IEEE Transactions on Power Delivery， 2014，29（3）: 1326-1334.

[13]张红颖，张加万，孙济洲.基于混合互信息的医学图像配准[J].计算机应用，2006，26（10）:2351-2353.

[14]李辉，戴旭初，葛洪魁，等.基于互信息量的地震信号检测和初至提取方法[J].地球物理学报，2007，50（4）:1190-1197.

[15]鲁文霞，马盈仓.实值信息系统上基于熵的属性约简[J].西安工程大学学报，2014（1）：128-132.

[16]王松伟，石美红，张正，等.基于熵和变异度的织物疵点图像分割方法[J].西安工程大学学报，2014（2）：207-212.

[17]Angermann M，Robertson P，Kemptner T，et al. A high precision referende data set for pedestrian navigation using foot-mounted inertial sensors[J]. Proceedings of The Royal Society.A，2004，11（2）: 1597-1611.

MEMS gyroscope signal denoise based on Shannon's entropy and EMD

WANG Chen-gang
（School of Urban Rail Transportation，Soochow University，Suzhou 215000，China）

MEMS（Micro Electro Mechanical System）gyroscope has widely use in vehicle navigation，rotation detection，robot localization etc.While MEMS gyroscope signal usually has large drift noise which makes the result of detection have obvious deviation.In this paper，we propose a method based on EMD and Shannon's entropy to de-drift on gyroscope signal.First，EMD-based method decomposes nonlinear and non-stationary signal into waves with modulated frequency and amplitude.Then，using Shannon's entropy criterion to distinguish noise with high-frequency and gyroscope signal with lowfrequency.The result of simulation and experimental verification shows that this method performs well in de-drifting.

EMD；Shannon's entropy；gyroscope signal；denoise

TN98

A

1674－6236（2017）10-0174-04

2016-04-17稿件编号：201604177

王晨钢（1992—），男，江苏苏州人，硕士研究生。研究方向：行走人室内定位。