球环分隔式角接触球轴承的装球合套条件

刘建志，黄振，祁百龙

（常州东风轴承有限公司，江苏 常州 213022）

符号说明

aiz——内圈中挡边宽度

By——内圈沟道半沟宽度（图3）

By1——内圈沟道与端挡边外圆之间的引导斜面轴向宽度（简称内圈引导斜面轴向宽度）

Cb——保持环全宽

Ce1——外圈沟道口引导斜面轴向宽度

Cbe1——保持环挡边引导斜面轴向宽度

d2d——内圈两端面挡边直径（简称内圈端挡边直径）

d2z——内圈轴向对称处挡边直径（简称内圈中挡边直径）

Dw——承载球球径

Dbw——分隔球球径

Dpw——承载球组与内圈沟道接触角为αi时的中心圆直径

D′pw——承载球组与内圈沟道接触角为-αimax时的中心圆直径

Dpwg——承载球与引导斜面中点相切时的中心圆直径

Dbpw——承载球组与内圈沟道接触角为αi时的分隔球组中心圆直径

D′bpw——承载球组与内圈沟道接触角为-αimax时的分隔球组中心圆直径

Dbpwg——承载球与引导斜面中点相切时的分隔球组中心圆直径

Deo——外圈沟道最大直径

Dbe——保持环沟道直径

Db2——保持环挡边直径

fi——内圈沟曲率系数

Lxo——承载球与内圈在沟道轴向中心接触时相邻两球的周向距离

Lx——承载球与内圈在沟道接触角αi位置接触时相邻两球的周向距离

Lxg——承载球与内圈引导斜面中点相切时的周向距离

Lyo——承载球与内圈在沟道轴向中心接触时2列承载球球心的轴向距离

Ly——承载球与内圈沟道接触角为αi时2列球球心的轴向距离

Ly′——承载球与内圈在沟道接触角 αi位置接触2列承载球球心的轴向距离

Lzw1——装球时保持环与承载球的接触点到承载球球心的轴向高度

M，N——中间参数

Z——单列承载球数量

αi——内圈公称接触角

αimax——内圈最大接触角

λbe——保持环引导斜面斜角

1 球环分隔式角接触球轴承结构特点和工作特性

文献［1］对球环分隔式角接触球轴承的特性和设计方法进行过分析探讨，这里仅简单介绍。

球环分隔式双列角接触球轴承的基本结构如图1所示，由1个双沟道内圈、2个单沟道外圈、2列承载球、1列分隔球、1个带沟道的保持环（类似深沟球轴承的外圈）以及连接环组成。较大的钢球主要起承受载荷的作用，称为承载球；较小的钢球主要起对承载球做周向和轴向分离作用，称为分隔球。

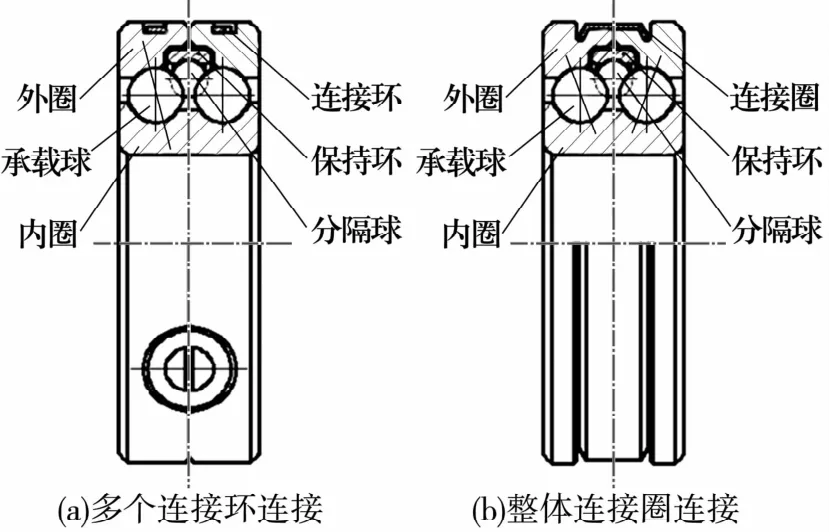
图1 球环分隔式双列角接触球轴承基本结构Fig.1 Universal separated double row angular contact ball bearings

球环分隔式双列角接触球轴承外圈有多个连接环和1个整体连接圈连接2种方式。多个连接环连接的特点是：外圈与座孔的配合面积大，配合刚度高，但外圈连接环槽加工困难，2个外圈和连接环铆合相对困难，工艺成本较高；整体连接圈连接方式的特点是：外圈连接圈槽加工容易，2个外圈和连接圈的滚压连接相对容易，因此工艺成本较低，但外圈与座孔配合的轴向宽度面积较小，配合刚度差。

球环分隔式双列角接触球轴承没有通常的保持架，主要靠保持环和分隔球的联合作用使承载球周向和轴向分离。

该轴承所有零件之间均为点接触，没有通常球与保持架的摩擦；与相同或接近规格的传统角接触球轴承相比，承载球直径小，受载后承载球与内外圈沟道的接触椭圆小；轴承内部空间比传统带保持架的角接触球轴承大；保持环兼有串油环的作用，使承载球和内外圈沟道得到充分润滑和热交换。因此该轴承适应高转速场合。

球环分隔式双列角接触球轴承没有保持架，可利用节省的周向和轴向空间来布置更多的承载球，从而提高其承载能力。与同外形尺寸的角接触球轴承相比，其基本额定动载荷可提高25%左右。

如果机构允许负游隙，可以使分隔球组外接圆直径与保持环沟道之间形成小的过盈配合，则保持环就存在由外向内的回复力，其回复力通过分隔球传递给承载球，使承载球与内外圈沟道保持适当的预紧状态（或补偿调节轴承的游隙），以提高轴承的接触刚度、承载能力及使用寿命。

2 球环分隔式角接触球轴承的装球合套

球环分隔式双列角接触球轴承由于零件多、工艺复杂、制造成本高，制约了该轴承的推广应用，其中装球合套是迫切需要解决的问题。

通过设计制造及计算发现，装球合套不仅仅是工艺上的问题，与产品设计也有关联。如果设计时只满足主机要求的载荷、转速等方面的性能要求，而忽略装球合套条件，则可能出现不能装球合套。

2.1 保持环能够套上分隔球组外接圆的条件

装球合套的条件是：保持环能够套上分隔球组的外接圆或分隔球能够进入保持环沟道。装球合套后各零件的几何关系如图2所示，承载球与内圈在沟道轴向中心位置接触时，2列承载球的中心距Lyo和Ly相差较小，同一沟道相邻两承载球球心距Lxo和Lx相差更小，图2中没有加以区别，但计算时必须区分。由图2和文献［1］可知分隔球组的中心圆直径为

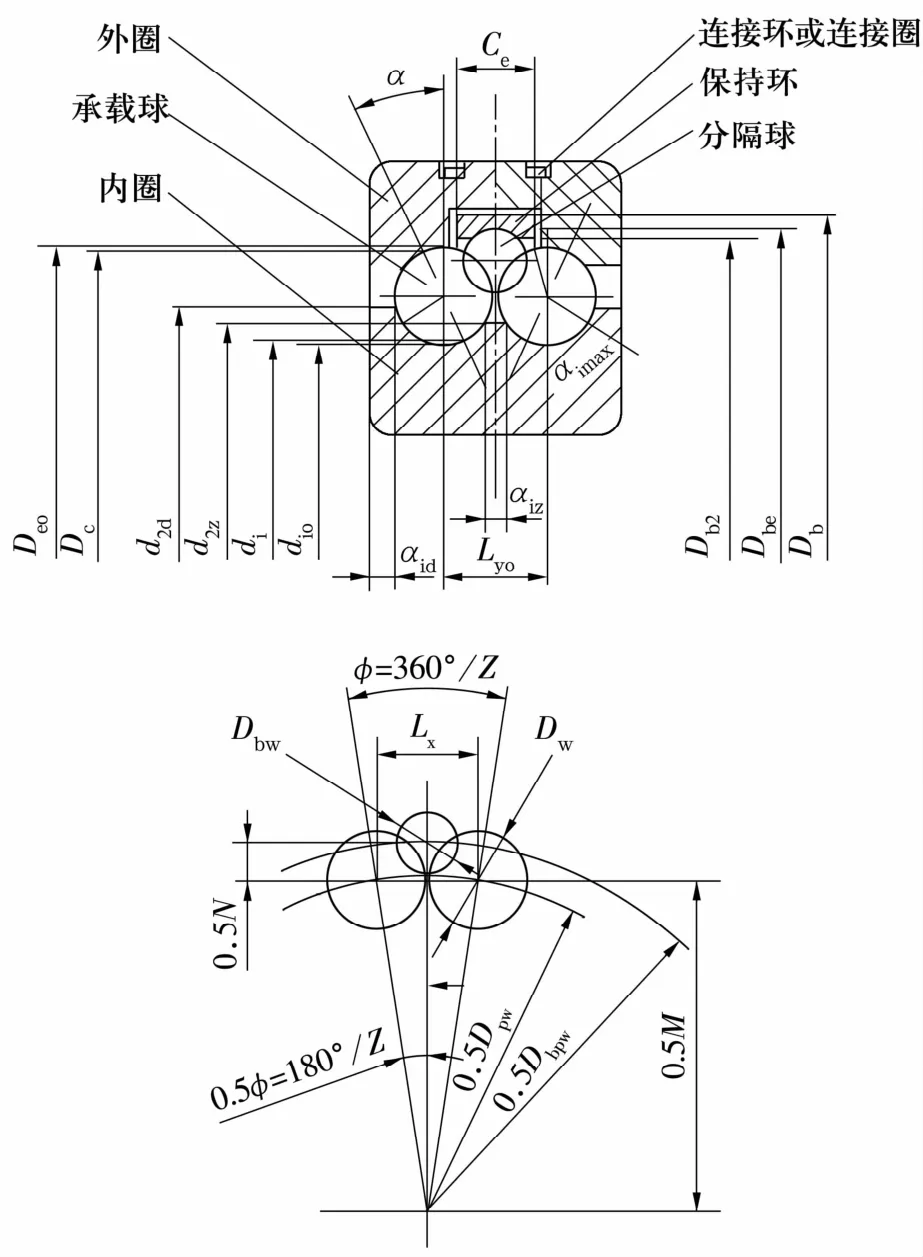
图2 装球合套后的几何关系Fig.2 Geometric relations after fitted with the ball

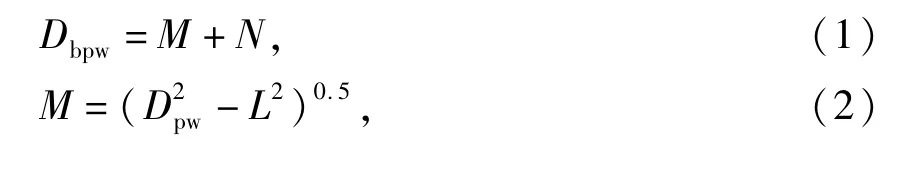
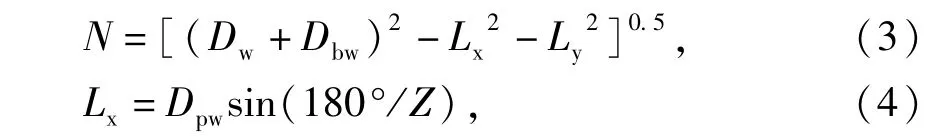
式中：M为与分隔球相切的4个承载球所在的平面到轴承轴线的2倍距离；N为分隔球的球心到4个承载球的球心所在平面的2倍距离；Dpw，Dw，Dbw，Ly由轴承设计主参数决定。

由图2可知，当分隔球组的外接圆直径小于保持环的挡边直径时，保持环沟道才能套在分隔球组的外接圆上。设想用保持环的挡边内孔压迫分隔球组，使分隔球组向轴承中心压缩，此时分隔球组的中心圆直径由Dbpw缩小为Dbpwg，其校核判别式为

即只有当分隔球组中心圆直径的缩小量大于或等于保持环沟径与挡边直径之差时，保持环才能套在分隔球组外接圆上。

当Dbpw缩小为Dbpwg时，M和 N缩小为 Mg和Ng，通过（2）式、（3）式可以看出，只有 Lx和 Ly增大为Lxg和Lyg时，才能使M和N缩小为Mg和Ng。

通过计算可知，当承载球与内圈沟道在靠近端面一边的最大接触角-αimax位置接触时，仍不能满足（5）式。只有当Ly增大到承载球与内圈沟道无接触时，即假想接触点离开沟道趋近内圈端面才能满足（5）式。因此，可通过增大内圈端挡边直径d2d，使内圈沟道圆弧端点 （即-αimax位置）与端挡边外圆之间有一引导斜面，当承载球在内圈引导斜面上的某个位置接触时，能满足（5）式。

与（5）式相关的参数较多，且参数之间相互制约，需要通过多次试算才能满足要求，故通过（5）式推导内圈端挡边直径计算公式的意义不大。为此，考虑合套时承载球滚动顺畅、承载球在引导斜面上有一定的调整空间、尽可能为实现自动或半自动装球合套预留空间等因素，假设：1）内圈沟道引导斜面与沟道圆弧端点相切；2）承载球在引导斜面中点与引导斜面相切。承载球在过渡斜面的中部位置与过渡斜面接触时的几何关系如图3所示，由图3可知，内圈引导斜面的径向高度为0.5（d2d-d2z），而引导斜面的轴向宽度为

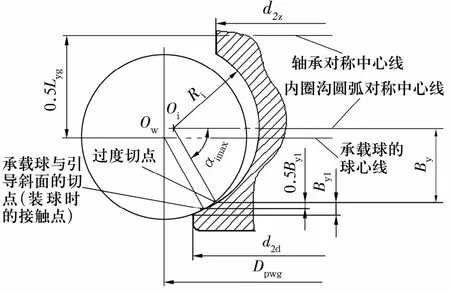
图3 承载球在引导斜面的中部位置与引导斜面接触时的几何关系Fig.3 Geometric relations between the middle position of the load bearing steel ball and the transition slope in the middle of the transition slope

当承载球与内圈引导斜面中点相切时

校核保持环能否套上分隔球组外接圆的过程为：① 用经验公式得到 d2d的初始值；②用（6），（9），（10）式计算 By1，D′pw，L′y；③用（7），（8）式计算 Lxg，Lyg；④用（2），（3）式计算 Mg，Ng；⑤用（1）式计算 Dbpwg；⑥用（5）式校核。

重复上述过程直到符合（5）式，实际设计可由计算机编程完成，主要是调整内圈端挡边直径，其次是调整保持环挡边直径、保持环沟径和分隔球球径。若调整后还不满足，则需调整其他设计主参数。

2.2 装第1列承载球的条件

装第1列承载球时的几何关系如图4所示。为了在装球时外圈不对承载球产生压痕，及第1列承载球进入内圈沟道后处于稳定状态，也为了增加装球空间便于实现自动或半自动装球，提高装球合套效率，将外圈沟道的内端设计为一个轴向宽度为Ce1、斜度为90°-αimax的引导斜面。由图4可以看出，承载球要通过A1和B1点形成的楔口进入内圈沟道，并与内圈引导斜面中点相切，必须使楔口宽度Q1大于承载球直径Dw，即

图4 装第1列承载球时的几何关系Fig.4 Geometric relations for loading the first column Load ball

（12）式为满足装第1列承载球的条件，该条件与内圈端挡边直径有关。

2.3 装分隔球的条件

装分隔球时相关零件的几何关系如图5所示。装分隔球之前，先将保持环套在第1列承载球组上。为使保持环在第1列承载球组上稳定，合套时保持环不对承载球产生压痕；为了给装第2列承载球预留较大空间，将保持环的挡边也设计为有引导斜面。

图5 装分隔球时的几何关系Fig.5 The geometric relations of Loading separating ball

前文讨论满足套装保持环条件 （5）式时，假设2列承载球组和1列分隔球组装好后再套装保持环，而这里是先装好第1列承载球组和保持环后再装入分隔球，感觉很矛盾。从产品结构和工艺上分析，装球后再装保持环非常困难。按照先装球后装保持环的思路讨论装保持环条件，是为了找到第1列承载球满足（5）式的位置，反之，只有满足（5）式，装第1列承载球和保持环后，分隔球才能进入保持环沟道，否则不能装第2列承载球。故（5）式是分隔球能够进入保持环沟道的必要条件。

下面讨论分隔球能够进入保持环沟道的充分条件。由图5可知，分隔球要进入保持环沟道，首先要通过内圈中挡边和保持环挡边形成的环形通道，也即分隔球要通过E和D，由此可得判别式为

另外，为了使分隔球能够流入保持环沟道，当分隔球通过E和D点与内圈中挡边接触时，Dbpwg大于Dpwg，分隔球在自身重力的作用下，按照图5中所示的方向流入保持环沟道，由此得到判别式

由（13）式、（14）式得

若内圈中挡边直径不能满足条件（15）式时，为保证能装球，必须满足（13）式。

2.4 装第2列承载球的条件

装第2列球时的几何关系如图6所示。承载球需通过A2和B2进入内圈沟道，与装第1列承载球相同，A2B2的宽度必须大于承载球直径，即

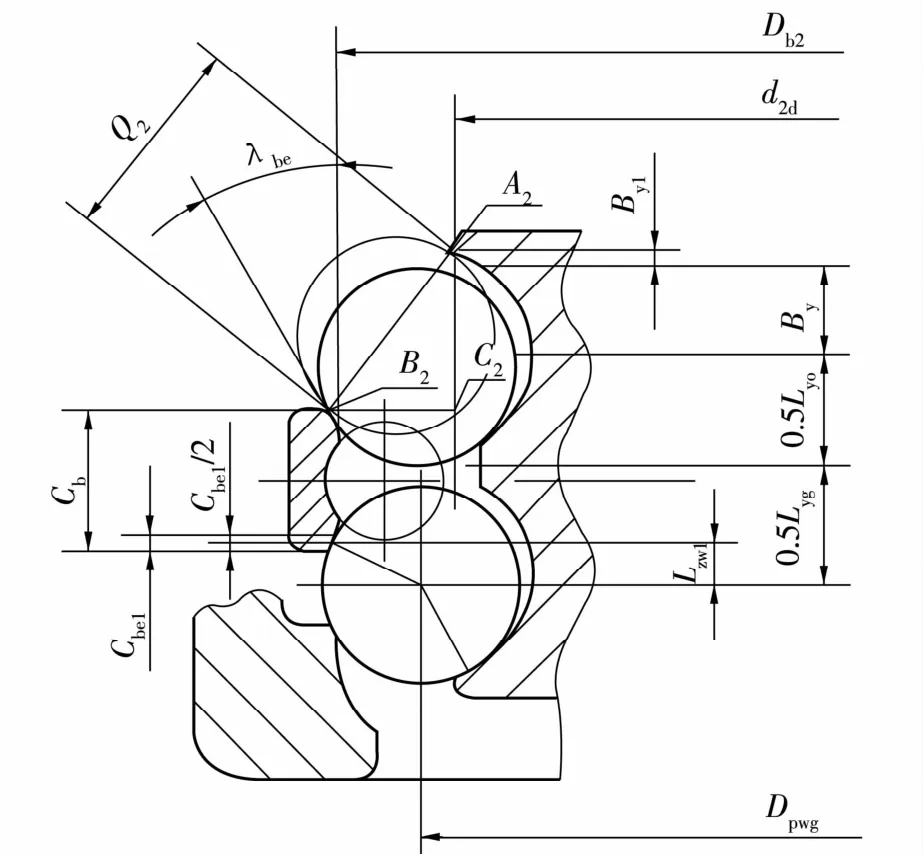
图6 装第2列承载球时的几何关系Fig.6 Geometric relations for loading the second column load ball

由（16）式可知，装第2列承载球的条件同样与内圈端挡边直径有关。保持环的装球引导斜面斜角λbe的近似值可由下式计算

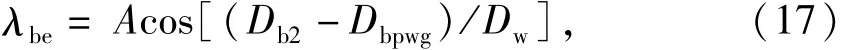
λbe的实际取值按稍小于（17）式的计算值圆整即可。

3 结束语

由设计实践和计算可知，对于球环分隔式双列角接触球轴承，如果仅仅在产品设计时满足主机的性能指标，而不考虑如何满足装球合套条件，则工艺上很难实现、甚至不能装球合套。从满足套装保持环的条件出发，通过计算承载球在内圈沟道不同位置（不同接触角）时分隔球组中心圆直径的变化规律，分析产品设计时，需要满足装球合套的几何条件，其中内圈端挡边直径最重要。一旦主参数确定，需调整内圈端挡边直径来校核能否实现装球合套。同时外圈沟道内端和保持环挡边设计有装球引导斜面，引导斜面不仅可以避免装球时外圈和保持环对承载球和分隔球造成的压痕，而且会增强装球合套过程中相关零件的稳定性，增加装球空间，便于实现自动或半自动装球合套。