移动式收缩型恶劣天气下改航模型和算法

王莉莉，王 鑫，位 放

(中国民航大学 天津市空管运行规划与安全技术重点实验室，天津 300300)



移动式收缩型恶劣天气下改航模型和算法

王莉莉，王 鑫，位 放

(中国民航大学 天津市空管运行规划与安全技术重点实验室，天津 300300)

针对边界匀速向内收缩且整体按一定加速度移动的恶劣天气危险区，考虑高空风对飞机航向的影响，提出了一种新的系统性改航方案，包括改航判断、两段式改航、航迹检查模型和改航侧验证模型。通过设计启发式算法，在第一段和第二段动态改航模型中，分别得到飞出改航起始点和飞向改航结束点方向。建立航迹检查模型，检测改航航迹与动态凸多边形危险区是否有冲突。经过反复调用所设计启发式算法以最小的角度调整来消除冲突，构造改航侧验证模型以确保最终改航航程最短。最后，通过对贵阳到长沙现有航路的仿真分析，验证了模型和算法的合理性。

空中交通管理;改航模型;移动式收缩型危险区;启发式算法

0 引言

近些年，随着国际油价低位徘徊和国内经济平稳发展，航空运输业进入快速发展期，旅客吞吐量大幅增加，但航班准点率一直不高，主要原因是危险天气所导致的航班延误[1]。改航飞行可以在一定程度上减少延误等待时间、提高机场运行效率、实现空域资源的高效利用，所以，安全有效绕过危险天气区域的改航飞行问题已经成为民航科研领域的重要研究方向之一。文献[2]针对静态危险天气，采用几何圆切法外推危险区来规划初始改航航迹。文献[3]针对不确定性天气条件下考虑云团动态位置的外推误差，建立了一种基于Markov链的单机动态不确定性改航规划模型，并用遗传算法进行了求解。文献[4]考虑改航飞行中的空中交通管制程序和飞机性能，给出了转弯角度、航段距离和改航点数量约束下的改航路径规划，提出基于几何算法的多边形改航策略。文献[5]从改航路线的安全性、经济性、管制员及飞行员的工作负荷、同计划航线的差异和航线飞行的舒适性5个角度出发，应用层次分析法，分别确定其在飞行空管评估模型、航空公司评估模型和综合评估模型下的权重，最后，对现有改航路径进行了评估。文献[6]提出改变高度的改航方式，考虑改航规则、相关约束条件建立的威胁概率模型和改航模型，确定飞机在何时何地以多大梯度爬升/下降，既可回避突发天气，又可避免与被穿越或被占用高度层上的飞机发生冲突。文献[7]解决了恶劣天气下过渡空域中的改航路径规划问题，提出了3种考虑不同要素的改航方法，第1种主要在标准进场航线的基础上提出的，第2种主要源于空中交通流量，第3种则是跟自由飞行相关，通过对比分析3种方法规划的路径，得出这3种改航策略都可以增加空域中容量的结果。文献[8]建立了可以预测航空器冲突的模型和以最小到达时间为目标的改航模型，并研究了恶劣天气下多架航空器产生飞行冲突时的避让改航问题，通过循环叠加非线性的偏微分方程求出最优解。

以上文献针对不同的改航情景提出了相应的改航策略，但在改航过程中，对危险天气区域面积的变化和位置的移动考虑甚少。所以，本文从飞机改航环境的现实情况出发，考虑了基于边界匀速向内收缩且整体按一定加速度移动的恶劣天气危险区的动态式改航模型。本模型避免了使用绕圆法对危险区做外接圆所导致的人为增加危险区面积，而且避免了将按一定规律变化的危险区经外扩后当作静止危险区进行改航。同时考虑了在改航过程中危险区周围高空水平风对航向的影响，以实时气象预报来预测危险天气的收缩和移动趋势，考虑到飞机转弯对舒适性的影响，只设置一个改航点。通过实例仿真分析验证了模型和算法的合理性和可行性。

1 改航判断

考虑到民航班机飞行规则、航线高度层配备、飞行员和管制部门工作负荷的原因，改航飞行一般简化为二维的临时航线规划问题。依照文献[9-10]中提出的方法，将卫星返回的气象预报信息处理成二维凸多边形,为了保证飞行安全，需要改航绕过危险区。

飞机是沿地面报告点Q1Q2…Qn之间连线对应上空指定高度层飞行的，假设飞机以速度Vc在预定航路飞行中遭遇恶劣天气需进行改航绕飞。依据民航相关规定，利用兰勃特等角圆锥投影法，构造以某一报告点为原点的XOY相对直角坐标系，X轴表示经度投影，Y轴表示纬度投影。根据气象云图及多普勒雷达，探测到某一时段内航路周围危险区边界向内收缩速度Vs，整体以加速度为a、速度为Vm进行变速移动，同时探测到在凸多边形危险区某一范围内有高空水平风，速度为Vw。考虑到改航有关规则，在预定航线上，分别取位于凸多边形危险区两侧以外且离其最近的两个报告点，作为改航起始点Qs和改航结束点Qf。如果随着凸多边形危险区整体移动，Qs或Qf被危险区域所覆盖，重新选取临近的报告点作为改航起始点或结束点。

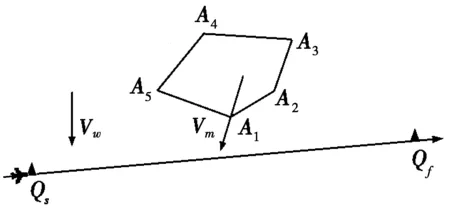
图1 飞机改航起始情景

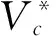
图2 凸多边形危险区与预定航线两种临界位置

图3为改航判断图，给出了4种不需要改航和2种需要改航的情况。图4为改航侧选择的临界位置。如图4所示，当凸多边形危险区正处于预定航线上时，以Qs为定点，分别向预定航线两侧危险区顶点做射线，使其分别与凸多边形危险区上下侧各相交于一个点。随着凸多边形危险区的收缩和移动，当上侧射线和预定航线所成角度与下侧射线和预定航线所成角度相同时，危险区所处相对位置是改航侧选择的临界位置，此时危险区顶点坐标为Li(xLi,yLi),i=1,2，…，n。这种临界位置选取的理论依据是在改航起始点和结束点固定的情况下，改航航迹与预定航线偏离角越小，改航航程越接近预定航程。∠L4QsQf=∠L1QsQf为改航侧判断临界角,∠B4QsQf为上侧改航的偏离角，∠C1QsQf为下侧改航的偏离角。如果∠B4QsQf>∠L1QsQf或∠C1QsQf<∠L1QsQf，则下侧改航；如果∠C1QsQf≥∠L1QsQf或∠B4QsQf≤∠L1QsQf，则上侧改航。

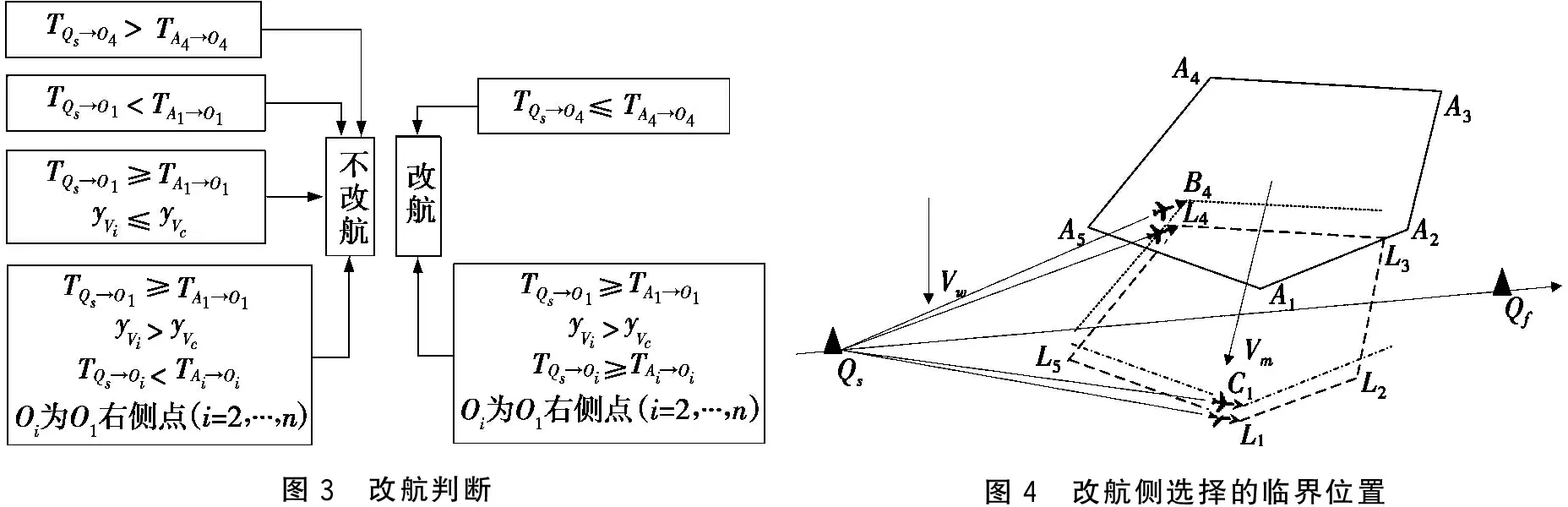
图3 改航判断图4 改航侧选择的临界位置

2 两段式改航模型构建及启发式算法设计

以下侧改航为例，设计改航模型并用启发式算法进行了分析,上侧改航模型与下侧改航模型原理相似。

如图4所示，t时刻，危险区移动速度为Vt，飞机位于Qs处。飞行中考虑危险区边界收缩及整体移动，为使临时改航飞行航程更短，构建一种飞机从Qs处开始,沿直线飞到危险区某顶点Bi所需时间与危险区从Ai(xAi,yAi),i=1,2，…，n移动到Bi(xBi,yBi),i=1,2，…，n所需时间都为△t1的模型，B1(xB1,yB1)可由下式得出:

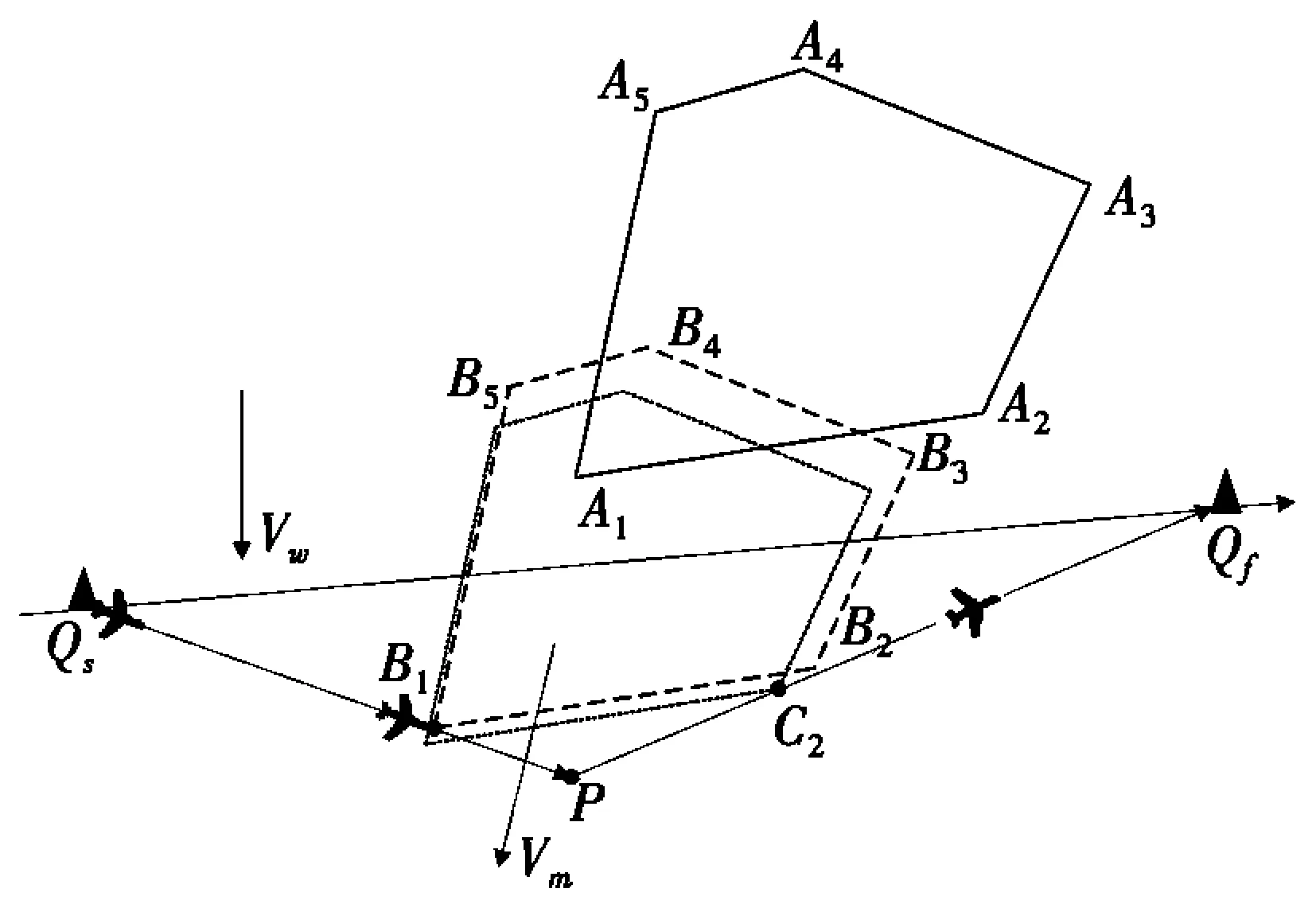
图5 两段式动态改航模型

(1)其中：Sm为危险区Ai(xAi,yAi),i=1,2，…，n经△t1移动的距离；S1为A1(xA1,yA1)经△t1收缩的距离。

图5为两段式动态改航模型图。由图5可知：t+△t1时刻，飞机位于B1处。飞行中考虑危险区边界收缩及整体移动，为使临时改航航程更短，构建一种危险区从Bi(xBi,yBi),i=1,2，…，n移动到Ci(xCi,yCi),i=1,2，…，n所需时间与飞机从B1处继续沿当前航迹方向飞到改航点P后转向直飞到顶点C2所需时间都为△t2的模型,P(xP,yP)可由式(2)得出。如果飞机在B1处转变航向直飞到Qf且整个过程不会与危险区有冲突，将不需要第二段改航飞行，B1即为改航点P。

(2)

其中：Sm为危险区Ai(xAi,yAi),i=1,2，…，n经△t1+△t2移动的距离；S2为A2(xA2,yA2)经△t1+△t2收缩的距离。

3 航迹检查及修正模型

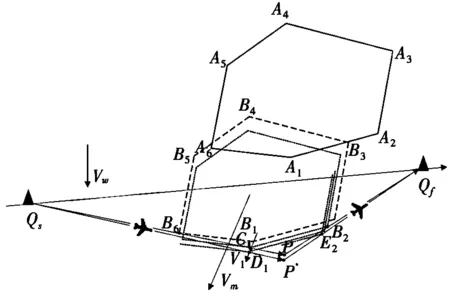
图6 第一段航迹检查及修正模型

图6为第一段航迹检查及修正模型图。如图6所示，在第一段动态改航模型中，当飞机位于B6时，如果当前改航航迹方向与危险区B6B1区段所成角度足够小，飞机继续沿此航迹方向飞行，可能与B6B1区段移动后位置冲突。飞机沿QsB6航迹方向将与A1移动轨迹相交于顶点C1。如TQs→C1>TA1→C1，即飞机与危险区之间有冲突，将对第一段的改航航迹方向进行修正，构造一种TQs→D1=TA1→D1=t1模型，即再次调用第一段动态改航模型，使飞机恰好通过B6B1区段移动后的位置。如飞机沿修正后的航迹方向QsD1继续飞行，还有可能进入后续区段移动后的位置，将再次调用修正模型直到消除冲突。D1(xD1,yD1)可由下式得出：

(3)

其中：Sm为危险区Ai(xAi,yAi),i=1,2,…,n经过t1移动的距离；S1为A1(xA1,yA1)经过t1收缩的距离。

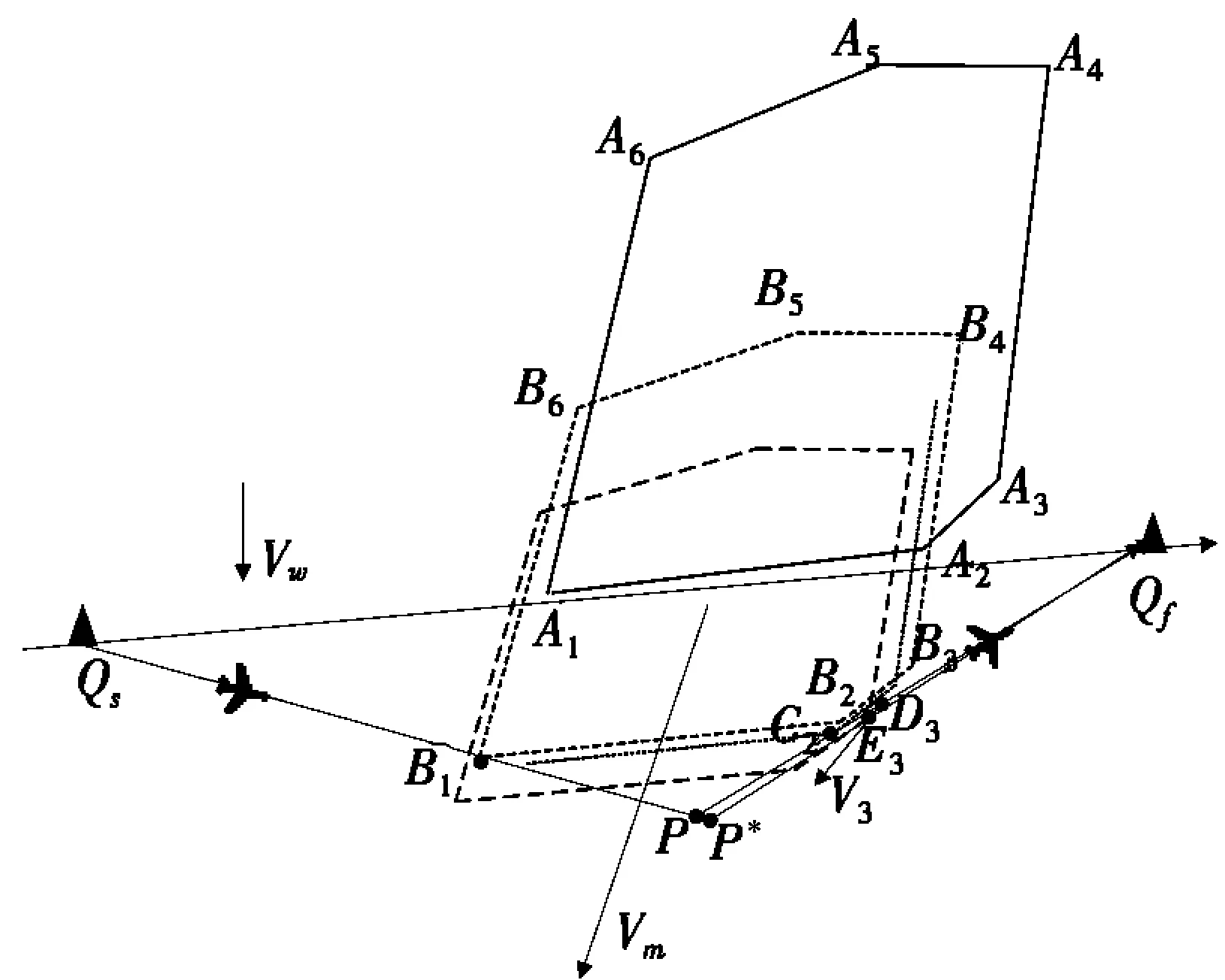
图7 第二段航迹检查及修正模型

图7为第二段航迹检查及修正模型图。如图7所示，在第二段动态改航模型中，当飞机位于C2时，如果当前改航航迹方向与凸多边形危险区C2C3区段所成角度足够小，飞机继续沿此航迹方向飞行，可能与C2C3区段移动后位置冲突。飞机沿PC2航迹方向将与A3移动轨迹相交于顶点D3，如果TA1→P+TP→D3>TA3→D3，即飞机与危险区之间有冲突，将对第二段的改航航迹方向进行修正，构造一种TA1→P+TP→E3=TA3→E3=t2模型，即再次调用第二段动态改航模型，使飞机恰好通过C2C3区段移动后的位置。如飞机沿修正后的航迹方向P*E3继续飞行还有可能进入后续区段移动后的位置，将再次调用航迹修正模型直到消除冲突。E3(xE3,yE3)可由下式得出：

(4)

其中：Sm为危险区Ai(xAi,yAi),i=1,2，…，n经过t2移动的距离；S3为A3(xA3,yA3)经过t2收缩的距离。

4 改航侧验证模型

为确保改航航程最短，本文设计了改航侧验证模型。如果飞机下侧改航偏离角与临界角相差30%以内且yVi和yVc方向相同，需再次利用上文改航模型计算上侧改航距离，在上下侧改航航程中取最小值。如果飞机上侧改航偏离角与临界角相差30%以内且yVi和yVc方向相同，需再次利用上文改航模型计算下侧改航距离，在上下侧改航航程中取最小值。

5 算例仿真分析

某一时段贵阳到长沙航路中有一段受移动式收缩型恶劣天气影响，需要侧向安全绕飞危险区。依据上文改航判断、两段式改航、航迹检查模型和改航侧验证模型，使用对应的启发式算法，经MATLAB7.0软件计算出相关点坐标及改航航程，验证模型和算法的合理性和可行性。

贵阳到长沙航班沿途报告点为:贵阳(KWE)-P173-P217-P293-怀化(ZHJ)-P159-老粮仓(LLC)-长沙(CSX)。飞机以650 km/h的巡航空速在此航段上飞行，气象部门获取某一时段内恶劣天气区域边界向内收缩速度为30 km/h。当飞机位于怀化(ZHJ)时，危险区整体移动速度为90 km/h，方向东偏北60°，且以0.01 km/h2加速度继续沿该方向移动，同时探测到在怀化(ZHJ)-P159航段周围有正北方向72 km/h的高空水平风。针对以上飞行环境需侧向绕飞危险区，将P217所在位置作为原点，通过飞行受限区划设和格雷厄姆算法，将气象雷达云图处理成凸多边形危险区A1～A6，某时刻飞机处于怀化(ZHJ)，这时怀化(ZHJ)及P159报告点在XOY相对直角坐标系中的坐标分别为(124.59,40.48)、(225.92,63.87)，且顶点坐标分别为A1(200.00,40.00)、A2(200.00,80.00)、A3(174.00,80.00)、A4(178.00,42.00)、A5(185.00,41.00)和A6(192.00,40.50)。

图8为贵阳—长沙改航模型。如图8所示，飞机需要改航绕过危险区，选取怀化(ZHJ)和P159作为改航起始点和结束点符合改航相关规则。通过模型和算法得 ∠B4QsQf=15.37°,∠L4QsQf=∠L3QsQf=16.94°,∠G4QsQf=18.82°,依据改航判断需进行下侧改航。依据第一段动态改航模型，可得B4(176.078,38.345)，将QsB4作为起始改航航迹方向。经航迹检查此航迹方向将在B4点与危险区冲突,需修正起始改航航迹方向，再次调用该模型进行修正使TQs→C5=TA5→C5，可得C5(181.36,37.01)，将起始改航航迹方向从QsB4修正到QsC5。经航迹检查此航迹方向将与危险区顶点A6的轨迹方向交叉于D6且TQs→D6>TA6→D6,与危险区冲突,需再次调用该模型进行修正使TQs→E6=TA6→E6,可得E6(190.46,32.75)。将起始改航航迹方向从QsC5修正到QsE6，此方向转弯前与危险区无冲突，所以起始改航航迹方向最终确定为QsE6。进入风区需要调整飞行速度为645.57 km/h，调整航向为北偏西89.7°，以使沿QsE6航迹速度保持在650 km/h,接下来将寻找结束改航航迹方向。

图8 贵阳—长沙改航模型

如图8所示，飞机将以危险区顶点A1作为结束改航衔接点。根据第二段动态改航模型，可得F1(198.26,34.67)，F1Qf和QsE6交叉于P1(195.85,32.12)为改航点，此结束改航航迹方向将与凸多边形危险区没有冲突,所以将F1Qf作为结束改航航迹方向。进入风区需要调整飞行速度为704.01 km/h，调整航向为西偏南50.6°，以使沿F1Qf航迹速度保持在650 km/h。改航航程为115.476 km，比预定航程(103.99 km)增加了11.04%，符合改航规则。

∠L4QsQf=16.94°,∠P1QsQf=15.9°,相差在30%以内,需进行改航侧验证。通过上侧改航模型和算法得上侧起始改航衔接点为G3(173.04,70.53)，将QsB4作为起始改航航迹方向，在飞到上侧改航点P2前不会与危险区产生冲突。飞机从Qs进入风区，需要调整飞行速度为690.67 km/h，调整航向为西偏南36.88°，以使沿QsG3航迹速度保持在650 km/h。如图8所示，飞机将以危险区顶点H2作为结束改航衔接点，根据第二段动态改航模型，可得H2(187.89,71.58)，H2Qf和QsG3交叉于P2(177.98,73.60)为改航点，此结束改航航迹方向将与凸多边形危险区没有冲突,所以将H2Qf作为结束改航航迹方向。进入风区，需要调整飞行速度为579 km/h，调整航向为北偏西77.11°，以使沿H2Qf航迹速度保持在650 km/h。改航航程为111.743 km，小于下侧改航航程(115.476 km)，比预定航程(103.990 km)增加 7.56%，符合改航规则。如果使用绕圆法和外推法改航，所需改航航程将超过111.743 km。因此，本文两段式改航模型和启发式算法，对于解决将危险区划设为凸多边形问题具有一定的优势。

6 结束语

本文针对移动式收缩型危险区，设计了一种新的系统性改航方案，该方法解决了将动态危险区看做静态改航而人为扩大危险区面积的缺陷。通过两段式改航模型来确定改航起始点和改航结束点，检查改航航迹和危险区之间的潜在冲突并反复调用启发式算法消除冲突。最后，通过改航侧验证模型来确保以最小的角度调整改航航迹，且以最短的航程安全绕过动态危险区。

[1] 杨新湦,齐莉,翟文鹏.航班时刻资源优化配置与延误水平评估[J].河南科技大学学报(自然科学版),2016,37(3):19-23.

[2] 王莉莉,杨惠东.飞行冲突条件下基于几何算法的改航策略研究[J].飞行力学,2012,30(5):466-469.

[3] 孟令航,徐肖豪,李善梅,等.不确定强对流天气下动态改航路径规划[J].西南交通大学学报,2012,47(4):686-691.

[4] 李雄,徐肖豪,朱承元,等.基于几何算法的空中交通改航路径规划[J].系统工程,2008,26(8):37-40.

[5] 李雄,徐肖豪.空中交通改航路径评估方法研究[J].飞行力学,2011,29(1):84-88.

[6] 王莉莉,周娟.突发天气条件下航空器改变高度的改航模型和算法研究[J].中国安全科学学报,2014,24(7):106-110.

[7] KROZEL J,PENNY S,PRETE J,et al.Comparison of algorithms for synthesizing weather avoidance routes in transition airspace[C].AIAA Guidance,Navigation and Control Conference.2004:1-9.

[8] PANNEQUIN J J,BAYEN A M,MITCHELL I M,et al.Multiple aircraft deconflicted path planning with weather avoidance constraints[C].AIAA Guidance,Navigation and Control Conference.2007.

[9] 李雄,徐肖豪,王超,等.基于凸多边形的飞行改航区划设及路径规划研究[C].中国控制决策会议.2008:3093-3088.

[10] 杨惠东,王莉莉.基于数值气象预报的飞行受限区自动划设[J].航空计算技术,2012,42(4):101-103.

国家自然科学基金项目(71571182);国家自然科学基金委员会与中国民用航空局联合基金项目(61179042);教育部人文社科青年基金项目(14YJC630185)

王莉莉(1973-),女,陕西兴平人,教授,博士,硕士生导师,主要研究方向为空中交通管理和空域规划.

2016-05-23

1672-6871(2017)03-0035-06

10.15926/j.cnki.issn1672-6871.2017.03.008

V355

A