一类高考试题的转化和拓展

安徽省繁昌县第一中学 (邮编：241200)

一类高考试题的转化和拓展

安徽省繁昌县第一中学鲍健(邮编：241200)

在高中数学中，错位相减法是用来推导等比数列前n项和公式的方法，是数列求和的重要方法之一，也是高考考查的重点方法.

1 提出问题，引发思考

笔者研究近几年各省市的高考数列解答题发现，用错位相减法求数列的前n项和的问题出现频率非常高.从下面所列举的部分高考试题，我们发现这些高考数列解答题第一问都是考查等差、等比这两种特殊数列的通项公式，第二问都是考查由等差等比对应项乘积构造新数列的前n项和.

是等差数列，且an=bn+bn+1．

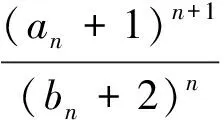
所以a1=11，当n≥2时，an=Sn-Sn-1=3n2+8n-3(n-1)2-8(n-1)=6n+5，

又an=6n+5对n=1也成立，所以an=6n+5．

当n=1时，2b1=11-d；当n=2时，2b2=17-d，

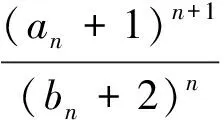
则Tn=6·22+9·23+…+(3n+3)·2n+1.

两边同乘以2，得：2Tn=6·23+9·24+…+(3n)·2n+1+(3n+3)·2n+2，

故Tn=-12+3·22(1-2n)+(3n+3)·2n+2=3n·2n+2．

(Ⅰ)求数列

的通项公式；

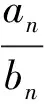
2Sn=3n+3．

2 探究问题，提炼结论

设an=dn+a0，bn=b1qn-1，(n∈N*)则：

=(d+a0)b1+(2d+a0)b1q+(3d+a0)b1q2+…+(nd+a0)b1qn-1，

①

②

综上所述，Sn=

3 转化问题，殊途同归

对于①式我们有

③

④

4 拓展问题，发现新知

⑤

由于⑤式中的各项均能求和，且此时不需要用错位相减法，所以这里就不过多赘述，即得：

当q≠1时，我们用数学归纳法证明：

考虑

当n的最高次数m=1时，此时即为结论1，命题成立.

假设当m=p(p∈N*)时命题成立，则当m=p+1时，

⑥

⑦

).

则由⑥-⑦得：

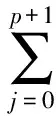
⑧

在⑧式第3项中i(i=1，2，…，n)的最高次数m=p，由假设知，当m=p时可以用错位相减法求和，故m=p+1时结论也成立.

综上所述，由数学归纳法可得拓展结论成立.

2017-04-08)