浅议对数学教材上习题的改编
2017-07-24安徽省颍上县第二中学邮编236200
安徽省颍上县第二中学 (邮编:236200)
浅议对数学教材上习题的改编
安徽省颍上县第二中学吴永剑(邮编:236200)
数学教学离不开习题教学,在用好教材提供的习题基础上,如果再恰当地改编、加工、重构教材习题,使得精选的习题更加符合学情,贴近学生生活,将会获得意想不到的教学成果.本文主要介绍个人在教学中改编教材习题的方法以及实践中获取的经验,愿与同行们交流一下.
1 习题改编的常见方法
1.1 改编习题形式
(1)常数字母化.即将已知命题或公式中的常数改为字母,从而使其适用范围扩大;例如求函数f(x)=x3+2x2的递增区间?改编为求函数f(x)=x3+ax2(a∈R)的递增区间?

(3)对象一般化.即将具体对象改为一般对象或抽象对象,从而使命题、公式得到推广或者舍弃具体对象的具体属性、抽象出共同的本质属性,从而建立新概念;
例如判断f(x)=3sin2x在R上奇偶性?改编为:讨论字母A、ω、φ、b在不同取值范围内,函数f(x)=Asin(ωx+φ)+b在R上的奇偶性?
1.2 改编习题结构
(1)将条件和结论互换.顾名思义就是运用逆反、辩证思想将问题的条件和结论互换.
(2)改编问题条件和结论的搭配
①条件开放型:有些习题满足结论的充分条件不唯一,改编时力求对它们有一个全面的考查;条件充要型:以某个知识点为载体,对所给的条件和结论进行充分性和必要性的研究;
②结论否定型;对原题的结论直接否定,而条件不变.结论开放型;所要寻求的结论有多种可能,而习题只要求寻找出一个正确的结论即可;
③结论探索型:归纳型探索题通过观察、比较、分析、抽象、概括、猜想、证明一系列步骤探索出一般性的结论;存在型探索题要按照存在与否采取不同方法给与解决,若存在,找出例证即可;若不存在,运用反证法证明.
④设问阶梯型;命题考查的对象情况过多或涉及知识综合性太强,为引导学生得出正确结论设置一组由易到难的问题串.
⑤改变表达方式:改变问题条件和结论的描述,使得问题情境更新颖或体现知识的内在联系,培养学生化归转化思想而设题.
例(2004年全国卷文19题)已知函数f(x)=ax3+3x2-x+1在R上是减函数,求a的取值范围.按照①—⑤改变习题的条件和结论的搭配方法,该高考题可改编为:
(1)求a的一个值,使得函数f(x)=ax3+3x2-x+1在R上是减函数?
(2)求a的取值范围,使得函数f(x)=ax3+3x2-x+1在R上不是减函数?
(3)是否存在a=-1,使得函数f(x)=ax3+3x2-x+1在R上是减函数?
(4)函数f(x)=ax3+3x2-x+1. (i)当a=-6时,求证:函数f(x)为R上减函数;
(ii)求a的取值范围,使得函数f(x)为R上减函数?
(5)讨论a的取值,使得导函数f′(x)=3ax2+6x≤1的在R上恒成立?
1.3 创造新题
(1)以新概念、新定义的形式改编出创新题

(2)以命题的结构改编出发散型创新题


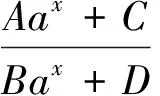
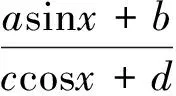

(3)通过命题的延伸改编出类比、归纳型创新题.

2 习题改编的心得体会
2.1 有效性
习题的改编要比之前原题更优,克服教材篇幅有限的局限性,克服教材语言过分简练、抽象等不足,改编教材习题要突出背景丰富,理解直观有效性;要深入分析改编题与原题之间的联系与区别,揭示原题的本质,考量改编题的作用,围绕教学目标改编,围绕学情创设情景,力求避免生搬硬套,复杂冗长题目出现;改编题要围绕知识难点设题,分解难点;围绕重点解析,透过现象指明本质;改编后的习题也要不断优化、再创新.
2.2 构建数学知识体系和思想方法体系
习题的改编要帮助学生将零碎的知识片段串起来,按照知识的形成构建体系,内化新知为学生客观认知;要按照学生的已有基础去设置问题,从知识的整体结构去看问题,理解、运用知识,避免学生搞题海战术;同时,按解决问题的方法去形成数学思想,避免就题论题,只见树木,不见森林,真正实现知识网络化需要数学思想的统帅,思想认知全面了,知识体系才完整.
2.3 培优性
改编习题要克服原题局限性即适合某个层次的学生,很难让所有学生受益;现代教育关注学生间的差异,设置不同层次的问题,要让习题教学使每个学生受益,培养学生思维深刻性、灵活性、发散性、创造性[2],让优生更优,后进生更进一步,真正实现习题培优功能;
事实上,作为一线教师,正确合理地改编、优化教材习题,以命题者的角度去思考教学,以教材编辑者的角度去理解教材、使用教材,有利于提高自己的专业素养和获取学生的信任.
1 徐章韬. 正弦定理在空间的推广[J]. 数学通讯(下半月),2005(9):32
2 陈玉娟. 在变式教学中培养学生的数学思维品质[J].高中数学教与学,2010(5):4-6
2017-03-16)
