共轴双旋翼飞行器建模及纵向姿态控制优化*

石征锦 宫政伟 赵方昕 马晓爽

1.沈阳理工大学自动化与电气工程学院， 沈阳110159 2.沈阳安瑞信科技有限公司， 沈阳110159 3.沈阳理工大学信息科学与工程学院， 沈阳110159

共轴双旋翼飞行器建模及纵向姿态控制优化*

石征锦1宫政伟2赵方昕3马晓爽1

1.沈阳理工大学自动化与电气工程学院， 沈阳110159 2.沈阳安瑞信科技有限公司， 沈阳110159 3.沈阳理工大学信息科学与工程学院， 沈阳110159

基于共轴双旋翼飞行器六自由度模型及其自身结构特点，建立了相关的动力学模型，并以该飞行器的纵向姿态控制为例，提出了一种带自动修正因子的Fuzzy-PID自适应优化方法。利用Matlab/Simulink搭建了共轴双旋翼飞行器纵向姿态控制系统模型并进行仿真，与传统PID控制和常规Fuzzy-PID控制进行了对比。实验仿真结果表明，该控制方法能够改善系统的静动态特性，具有较好的自适应能力。 关键词 共轴双旋翼飞行器；六自由度模型；模糊控制；修正因子；PID

多年来，无人机自主飞行控制一直是航空领域的研究热点。共轴双旋翼飞行器与其它固定翼飞行器相比，无需尾翼，结构紧凑，利用上下共轴反转的2组旋翼来平衡扭矩，在狭小的空间实现垂直起降、多方向飞行及悬停等方面具有很大优势。因此在军事和民用领域都有着广泛的应用价值。一般的无人机姿态控制系统分别对其纵向、横侧向和航向三个通道进行协调控制。其中，纵向通道控制设计最为关键复杂，其控制率的优劣会影响无人机的各项飞行性能。文献[1]采用了一种局域RBF神经网络与PID控制相结合的方法对飞行系统进行动态调参，改善了控制效果，但RBF控制器网络的隐含层节点个数和参数难以确定。文献[2]提出了一种带固定修正因子的模糊控制技术，与简单模糊控制相比在一定程度上改善了其控制性能，但是采用固定参数的模糊控制器不能保证系统在大范围内获得最优的动静态性能。

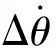
1 共轴双旋翼飞行器模型的建立与空

气动力学分析

1.1 六自由度模型建立

在建立机体动力学方程时，对共轴双旋翼飞行器作如下假设：

1)共轴双旋翼飞行器为刚体，且飞行器质量恒定；

2)几何外形和质量分布都有比较好的对称性，以oxbzb面或oybzb面为对称面；

3)忽略地球曲率；

4)重力加速度不随飞行高度变化；

5)不考虑飞行器结构弹性形变和气动弹性的变化。

基于上述假设，将共轴双旋翼飞行器视为理想刚体，因此它遵循刚体运动建模的一般方法和原则，根据刚体力学和运动学建立共轴式双旋翼飞行器的六自由度飞行动力学以及空气动力学模型。

在描述共轴双旋翼飞行器的数学模型和不同飞行状态时，首先要建立2个常用坐标系：地面坐标系E(O,xe,ye,ze)和机体坐标系B(O,xb,yb,zb)。根据机体坐标系和地面坐标系之间的几何关系，可得到飞行器质心位置与运动速度之间的运动学关系：

(1)

其中，(x,y,z)为飞行器重心在地面坐标系中的位置；(ψ,θ,φ)为相对地面坐标系的姿态角，即偏航角、俯仰角和翻滚角；(u,v,w)是机体质心运动速度在机体坐标系下的三轴分量。

机体六自由度运动方程[3]为：

(2)

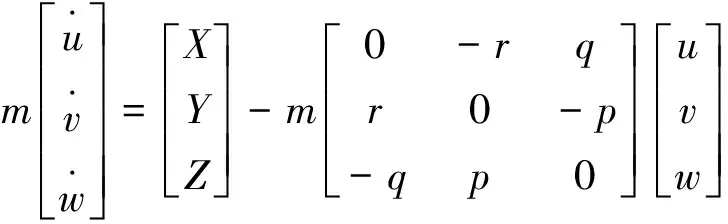
(3)

(4)

其中，I是惯性矩阵，其非对角元素可近似为0，(X,Y,Z)是作用在共轴双旋翼飞行器上的合外力ftot在机体坐标系的各坐标轴上的分量；(L,M,N)是共轴双翼飞行器所受力矩之和M在机体坐标系各坐标轴上的分量；(p,q,r)为飞行器绕机体三轴的角速度。

1.2 空气动力学模型

为简化其数学模型，可将该共轴双旋翼飞行器简化看作由上、下两对旋翼和一个高为l、半径D为的圆柱体组成。对该飞行器的动力学分析主要有上、下旋翼产生的升力、气流干扰对机体的作用力及飞行器所受力矩。

共轴双旋翼飞行器基本结构如图1所示，分别以上、下旋翼的桨毂处为坐标原点，建立上、下旋翼坐标系O1(xr1,yr1,zr1)和O2(xr2,yr2,zr2)，以机体重心为坐标原点建立机体坐标系B(O,xb,yb,zb)。

图1 共轴双旋翼飞行器结构图

在上旋翼坐标系中，可将上旋翼产生的升力表达为：

(5)

其与上桨叶的升力系数α和工作转速ω1成比例，α与桨叶形状、尺寸以及飞行器状态有关。

下桨叶产生zb方向的垂直升力，除此之外，还产生xb和yb方向的2个横侧力，这是由于下旋翼桨叶桨距角整体性或者周期性的改变，能有效地改变其空气动力。下桨叶升力T2的表达式为：

(6)

其中，R(δcx,δcy)是机体坐标系B(O,xb,yb,zb)和下旋翼坐标系(O2,xr,yr,zr)的转换矩阵，β是下旋翼升力系数，ω2是下旋翼桨叶工作转速。

由于在正常运转时上、下旋翼间存在气动干扰，必然有气动效率的损失，2对旋翼在zb方向上产生的总升力T肯定小于Τ1与T2之和。因此两对旋翼产生的总升力T可表示为：

(7)

其中，损失系数0.8≤σ≤1。

共轴双旋翼飞行器在实际飞行中会受到阵风等随机因素的干扰。将这一因素考虑在内，影响飞行器气流的因素主要包括由旋翼产生的气流速度Vprop、机体自身平动或旋转产生的气流速度Vbody及外部风产生的气流速度Vwind，一般是不可预测的。

由机械能守恒定律可得总的气流干扰在机体坐标系3个坐标轴上的分量为：

Vux=-u+[Vwind]xb

(8)

Vvy=-v+[Vwind]yb

(9)

Vwz=

(10)

则气流作用在飞行器上的力fbody在机体坐标系各方向轴上的分量可表示为：

(11)

(12)

(13)

(14)

其中，T是2对旋翼产生的升力和；fbody是气流作用在机体上的力；fp是飞行器自身重力：

(15)

空气动力力矩分为滚转力矩L、俯仰力矩M和偏航力矩N。由式(6)可得2个侧向力矩L和M分别为：

(16)

(17)

其中，d为质心G与下旋翼中心O2的距离。

偏航力矩N是由两对旋翼产生的，与它们各自

的气动系数γ1，γ2和旋转速度ω1，ω2成比例：

(18)

以上部分建立了该共轴双旋翼飞行器各部分的气动模型，将气动力及力矩表达式代入到飞行器运动方程中，得到了该共轴双旋翼飞行器非线性飞行力学模型。

2 带修正因子的模糊PID自适应控制

共轴双旋翼飞行器的运动是复杂的非线性运动，对其直接求解十分困难。通常是将其非线性飞行模型线性化，再对线性模型进行控制律设计。本文以共轴双旋翼飞行器的纵向俯仰姿态为例，采用小扰动线性化方法，将其纵向运动方程式线性化，得到其纵向短周期运动状态方程为：

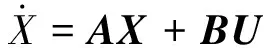
Y=CX

(19)

2.1 系统设计

共轴双旋翼纵向姿态控制器由2部分组成：Fuzzy控制器和PID控制器。根据俯仰角偏差Δθ来决定采用何种控制算法实现飞行器的俯仰姿态闭环控制。当俯仰角偏差较大时，采用模糊控制算法，加大控制作用抑制超调，提高系统的响应速度，使实际俯仰角尽快达到给定值；当俯仰角θ大小接近系统稳态工作点时，切换到PID控制，提高系统稳态精度，改善系统静态特性。图2为Fuzzy-PID自适应系统控制框图。

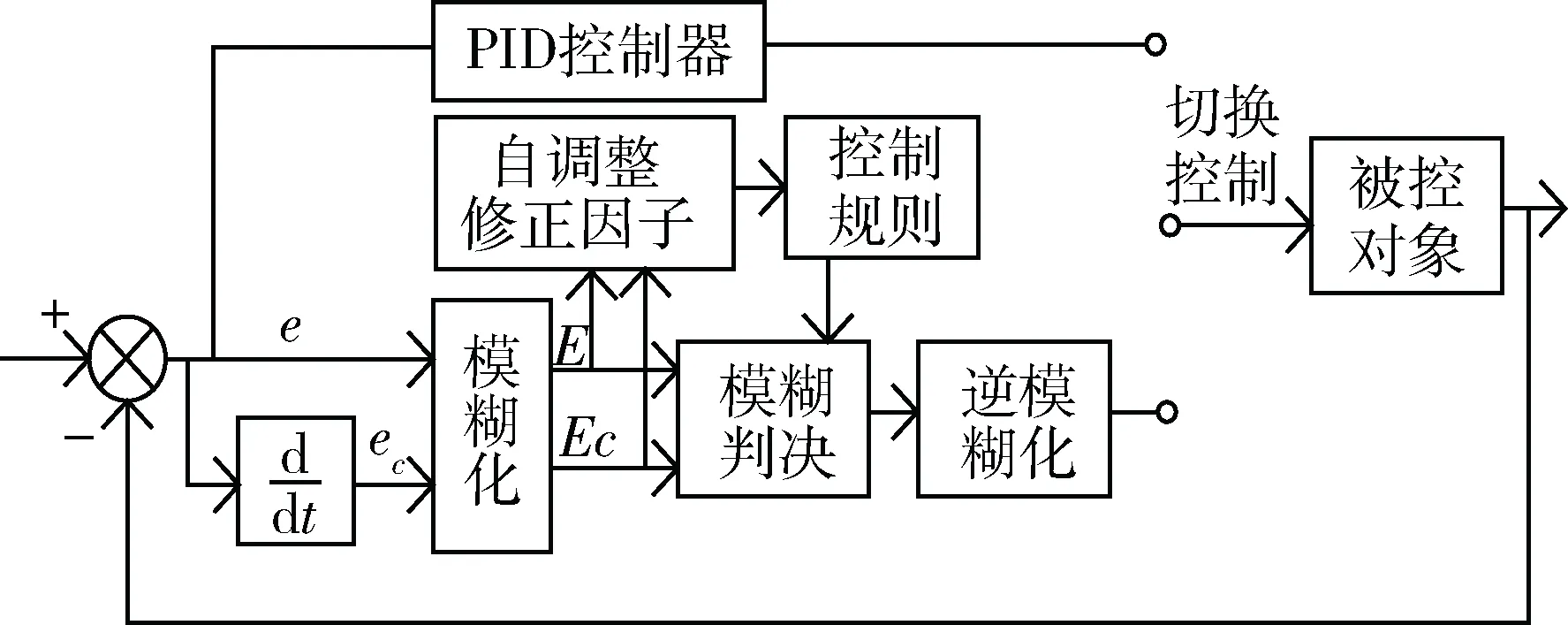
图2 系统控制结构框图

2.2 控制规则

表1 模糊控制规则表

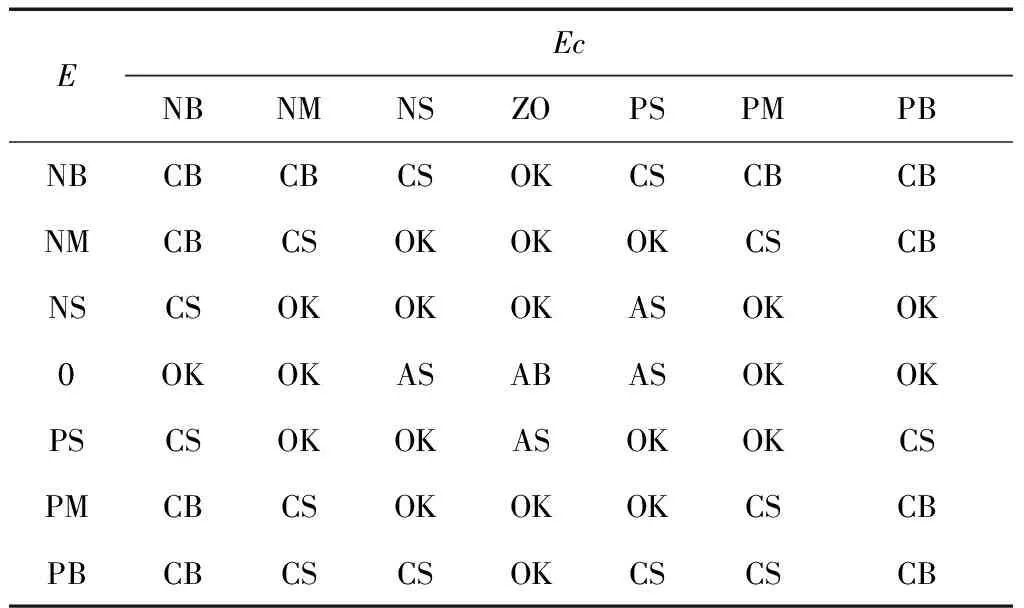
表2 修正因子n调整规则表

3 系统仿真

在MATLAB7.0/Simulink环境下，采用上述设计的带修正因子的模糊PID自适应控制器对该共轴双旋翼飞行器纵向通道(俯仰姿态)搭建Simulink模型并仿真。系统仿真框图如图3所示。给定俯仰初始姿态角θ=10°。

图3 系统仿真框图

将带修正因子Fuzzy-PID控制方法与PID控制、常规Fuzzy-PID控制方法作对比。图4给出在PID控制方法和常规Fuzzy-PID控制方法下，俯仰角输出、俯仰角速率、误差及误差变化率的响应曲线。图5给出了带修正因子Fuzzy-PID方法下的俯仰角输出、俯仰角速率、误差及误差变化率的响应曲线。从图4看出，同一坐标内传统PID控制方法和常规Fuzzy-PID控制方法下的俯仰姿态角的调节时间和超调量有大幅度减小，动态响应速度较快，过渡过程更加平稳，俯仰角速率的峰值也有所减小，飞行器俯仰通道的控制性能有所改善。从图5看出，在加入自动修正因子n后，与常规Fuzzy-PID相比，上升速度更快，系统响应时间在1s之内；超调不超过3%，更能适应共轴双旋翼飞行器复杂飞行环境的要求。

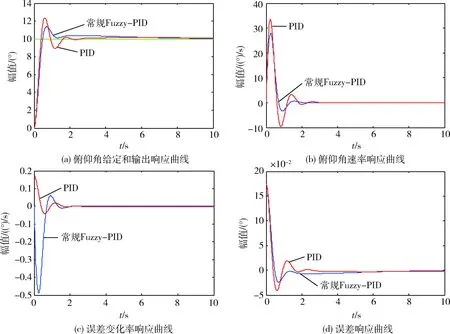
图4 PID和常规Fuzzy-PID控制时响应曲线

图5 带修正因子Fuzzy-PID控制时响应曲线

4 结论

针对共轴双旋翼飞行器的结构特点，在分析六自由度模型的基础上，建立了共轴双旋翼动力学模型。以纵向通道控制系统为例，本文将Fuzzy控制和PID控制相结合，提出了一种带自动修正因子的Fuzzy-PID纵向姿态控制方法。仿真结果表明，与传统PID和常规Fuzzy-PID方法比较，该控制方法可以快速减小俯仰姿态角偏差，稳态误差几乎为0，具有较强的自适应能力，达到了较理想的控制效果。

[1]Yanli,SaratchandranP,NarasimhanSundararajan.StaleNeuro-Flight-ControllerUsingFullyTunedRadialBasisFunctionNetworks[J].JournalofGuidanceControl,andDynamics， 2001, 26(4): 7-8.

[2] 张义捷, 钟友武, 许得军. 基于模糊控制技术的飞行器姿态控制系统设计[J]. 航天控制, 2013, 31(2): 28-32. (ZhangYijie,ZhongYouwu,XuDejun.TheAerocraftAttitudeControlSystemDesignBasedonFuzzyLogicControl[J].AerospaceControl, 2013, 31(2): 28-32.)

[3] 周国仪, 胡继忠, 曹义华, 王晋军. 共轴式直升机飞行动力学仿真数学模型研究[J]. 航空学报, 2003, 24(4): 293-295.(ZhouGuoyi,HuJizhong,CaoYihua,WangJinjun.ResearchonaMathematicalModelforCoaxialHelicopterFlightDynamics[J].JournalofAeronautics, 2003, 24(4): 293-295.)

[4] 方振平, 陈万春, 张曙光.航空飞行器飞行动力学[M].北京: 北京航空航天大学出版社, 2005.(FangZhenping,ChenWanchun,ZhangShuguang.AeronauticsAircraftFlightDynamics[M].Beijing:BeijingUniversityofAeronauticsandAstronautics, 2005.)

[5] 诸静. 模糊控制原理与应用[M]. 北京: 机械工业出版社, 2005.(ZhuJing.FuzzyControlPrincipleandApplication[M].Beijing:ChinaMachine, 2005.)

[6] 吴森堂, 费玉华. 飞行控制系统[M]. 北京: 航空工业出版社, 2006.(WuSentang,FeiYuhua.FlightControlSystem[M].Beijing:AeronauticsIndustry, 2006.)

[7]SalihAL.ModellingandPIDControllerDesignforaQuadrotorUnmannedAirVehicle[J].IEEEAQTR., 2010, 39 (5):697-699.

[8] 马晓爽, 石征锦. 一种改进Fuzzy-PID技术的飞行器姿态控制系统设计[J]. 电子技术应用, 2016, 42(10): 21-23,28. (MaXiaoshuang,ShiZhengjin.AnImprovedFuzzy-PIDTechnologyofVehicleAttitudeControlSystemDesign[J].ApplicationofElectronicTechnique, 2016, 42(10): 21-23,28.)

Coaxial Double Rotor Aircraft Model and Optimization of Longitudinal Attitude Control

Shi Zhengjin1，Gong Zhengwei2，Zhao Fangxin3，Ma Xiaoshuang1

1.Shenyang Ligong University, Institute of Automation and Electrical Engineering, Shenyang 110159, China 2. Shenyang Anruixin Technology Co., LTD., Shenyang 110159, China 3.Shenyang Ligong University, Institute of Information Science and Engineering, Shenyang 110159, China

Basedonsixdegreeoffreedommodelanditsstructurecharacteristicsforthecoaxialdoublerotoraircraft,itsownrelateddynamicsmodelisestablished,andthelongitudinalattitudecontrolofaircraftistakenforcasestudy,aFuzzy-PIDadaptivemethodwithautomatictuningfactorisproposedinthispaper. Matlab/SimulinkisusedtobuildthemodelofcoaxialdoublerotoraircraftlongitudinalattitudecontrolsystemandcomparedwiththetraditionalPIDcontrolandconventionalFuzzy-PIDcontrol.Theexperimentalsimulationresultsshowthatthestaticanddynamiccharacteristicsofthesystemcanbeimprovedandbetteradaptiveabilityisachievedbyusingthismethod.

Coaxialdoublerotoraircraft;Six-degree-of-freedommodel;Fuzzycontrol;Tuningfactors; PID

*国家自然科学基金-磁控形状记忆合金逆效应机理、模型及传感器研究(51377110)

2016-06-20

石征锦(1963-)，男，辽宁人，教授，主要研究方向为智能信息处理和自主飞行控制；宫政伟(1986-)，男，河北人，工程师，主要研究方向为智能信息处理和自主飞行控制；赵方昕(1996-)，女，江苏人，本科，主要研究方向为智能控制；马晓爽(1992-)，女，山东人，硕士研究生，主要研究方向为智能控制与导航。

TP 273

A

1006-3242(2017)03-0024-06