基于实数编码自适应遗传算法的整周模糊度快速解算*

易清明 易夕冬 石 敏

暨南大学信息科学技术学院，广州510632

基于实数编码自适应遗传算法的整周模糊度快速解算*

易清明 易夕冬 石 敏

暨南大学信息科学技术学院，广州510632

针对整周模糊度解算中实时性不强的问题,提出了一种基于实数编码的自适应遗传算法。首先利用卡尔曼滤波求解整周模糊度的浮点解，然后采用排序和多次(逆)双乔里斯基分解对浮点解及其协方差阵进行降相关处理，降低整周模糊度各分量之间的相关性，最后利用已知基线确定模糊度搜索空间，基于实数编码，将自适应遗传算法应用在整周模糊度的搜索解算过程中，求得整周模糊度的最优解。仿真结果表明，本文算法与Lambda算法相比,耗时更少；与简单遗传算法相比,具有更强的收敛能力，是一种高效的整周模糊度快速解算方法。 关键词 整周模糊度；卡尔曼滤波；乔里斯基分解；实数编码；自适应遗传算法

整周模糊度的快速解算是利用GPS载波相位作为观测量进行高精度实时相对定位的关键[1]。目前，求解整周模糊度的方法中理论体系最完备、应用最广的是Lambda算法[2]。但是其搜索空间较大，计算相对复杂，搜索效率并不高。遗传算法是由美国J Holland教授提出，具有内在并行性，全局优化性和稳健性的特点，但在实际搜索过程中，由于其交叉概率和变异概率保持不变，使得算法容易陷入局部最优[3]。因此本文提出一种基于实数编码的自适应遗传算法，简化搜索过程，提高寻优能力。

1 整周模糊度浮点解及其搜索空间

为了消除载波相位中电离层误差、对流层误差、卫星钟差和接收机钟差等大部分误差，在GPS精密定位中，常采用载波相位双差观察值进行处理。设t时刻，k,i两接收机观测了j,o两颗卫星，则载波相位双差观测方程为[4]:

(1)

为方便计算机建模与仿真，将其线性化后[5]建立常加速度模型下的卡尔曼滤波器,其状态方程和量测方程分别为：

Xk=Φk,k-1Xk-1+Гk-1Wk-1

(2)

Zk=HkXk+Vk

(3)

其中，Xk为包含接收机位置参数和双差模糊度的状态向量，Φk,k-1为状态转移矩阵，Гk-1为系统噪声矩阵；Zk为双差模式下的观测值向量，Hk为量测矩阵，Vk为观测噪声。根据平差测量原理[6]，当有t个历元j+1颗卫星时，估计参数的协方差矩阵为：

Q=σ2(HTM-1H)-1

(4)

其中，σ为估计参数的单位权均方差，M为载波相位双差观测量的权矩阵。

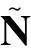
(5)

其中，N为j个双差整周模糊度组成的向量。对于长度为L的基线，每个双差整周模糊度Nn(n=1,2,…, j)的取值范围都在以浮点解为中心的L米基线范围内[7]，即:

-L/λ≤Nn≤L/λ

(6)

其中，λ=19.03cm，为L1载波。由式(6)可知，当L=2m时，整周数取[-10,10]间的21个整数。

2 基于实数编码自适应遗传算法的整

周模糊度求解

实数编码自适应遗传算法是一种高效稳健、并行全局的搜索算法，它能简化所求参数，并在搜索过程中自适应地调整遗传算法的交叉概率和变异概率，以求得全局最优解。在求得整周模糊度浮点解及式(6)搜索空间的基础上，通过设计本文的遗传算法，包括编码，设定适应度函数和遗传算子等操作，对式(5)的目标函数进行搜索寻优。

2.1 基于排序的Cholesky分解降相关

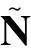
(7)

由式(5)和(7)可以得到降相关后的目标函数式(8)：

(8)

2.2 实数编码

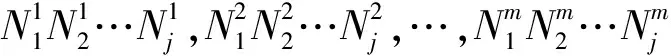
2.3 适应度函数和遗传算子

经过编码后，通过设定适应度函数和遗传算子对目标函数进行寻优。遗传算法是以目标函数为基础确定适应度函数，以确定最优解。对于式(8)的目标函数，通常选取式(9)作为适应度函数[11]:

f(N)=b-lg(G(N))

(9)

其中，b为一个足够大的正数，保证f(N)>0,对目标函数取对数是为了缩小各整周数组合之间的差值，避免遗传算法早熟，陷入局部最优。

在确定适应度函数后，利用轮盘选择算子进行最优值的选取。模拟轮盘的转盘，每个个体被选择的期望数量与其适应度值和群体平均适应值的比例有关。按照适应度比例选择，个体的适应度值越大，则被选中的概率越大[12]；交叉是结合来自父代交配种群中的信息产生新的个体，本文采用的是文献[13]中的交叉算子；变异是子代基因按小概率扰动产生的变化，本文采用的是对称变异和随机变异相结合的变异算子[14]。

2.4 自适应调整

Srinvivas等提出了一种自适应遗传算法(AGA)[15]。适应度高于群体平均适应度favg的个体对应较低的交叉概率Pc和变异概率Pm，使该解得以保护进入下一代；而低于favg的个体则对应较高的Pc和Pm，使该解被淘汰。其原理如图1所示。

图1 自适应遗传算法原理图

图1中， fmax为每代群体中的最大适应度， f ′为要交叉的2个个体中较大的适应度值， f为要变异个体的适应度，k和k′在(0,1)间取值。为了使群体中最大适应度个体的Pc和Pm不为0，分别将它们提高到Pc2和Pm2，这就相应地提高了群体中表现优良个体的Pc和Pm，减小了群体进化初期陷入局部最优的可能性。综上，Pc和Pm计算表达式如下[12]：

(10)

(11)

其中，Pc1=0.9, Pc2=0.6, Pm1=0.1， Pm2=0.001。经过自适应调整后，Pc和Pm能提供相对某个解的最佳Pc和Pm，在保证群体多样性的同时，也保证了算法的收敛性。

2.5 解算流程

首先利用基于排序的Cholesky分解,对双差方程求解出的整周模糊度浮点解及其协方差阵进行降相关处理，然后在确定了以上实数编码自适应遗传算法的各项参数后，利用本文算法对整周模糊度进行解算，其解算流程如图2所示。

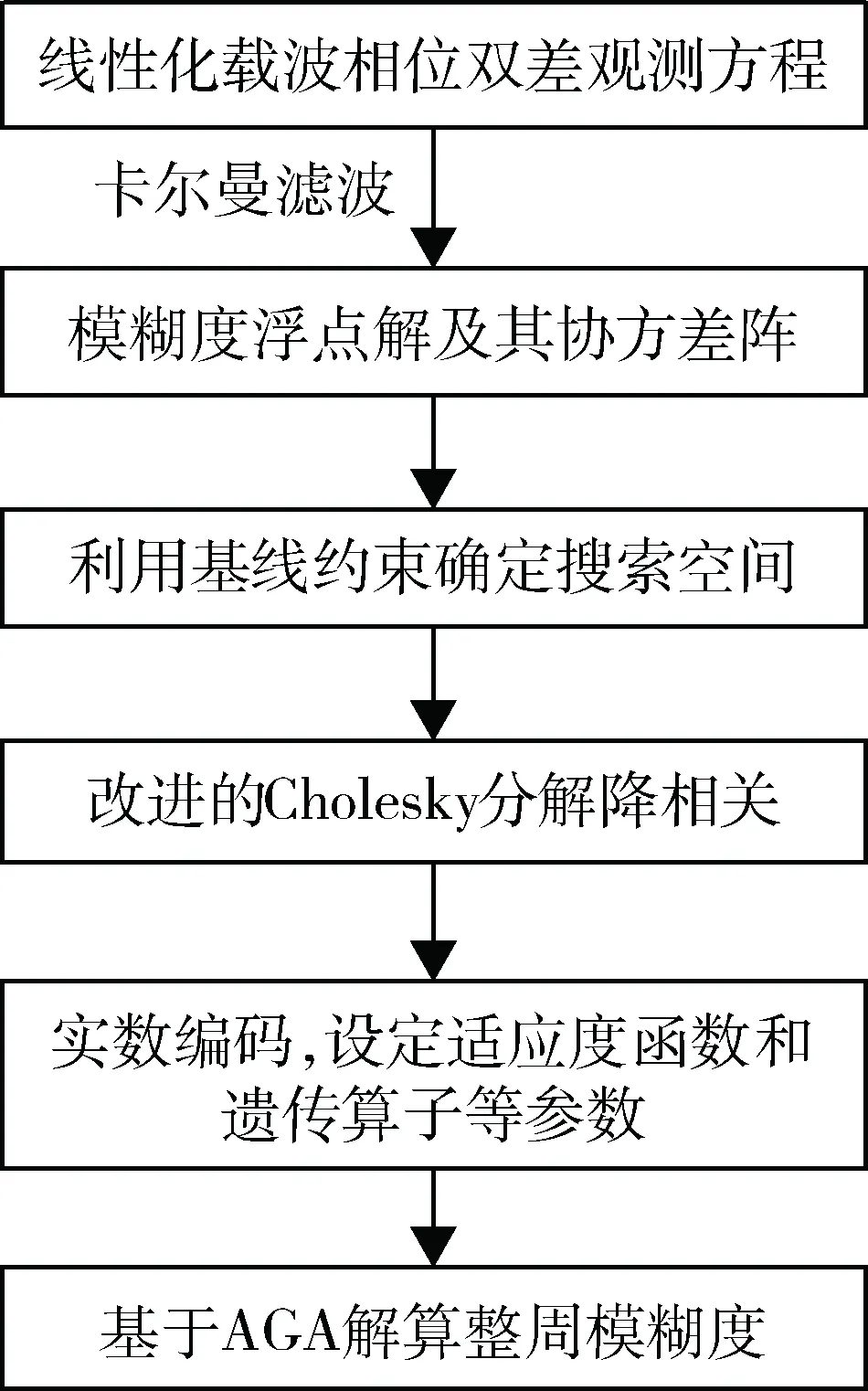
图2 解算流程图

3 仿真及结果分析

对上述方法进行仿真，采用文献[16]的解算实例,基线长为2m,由式(6)可知，每个整周模糊度的取值范围为[-10,10]。为了分析本文降相关算法的有效性，采用去相关系数R和矩阵的谱条件数E作为评价变换后协方差阵的去相关程度的衡量标准[9]，其参数如表1所示。

表1 去相关程度对比分析结果

由表1可知，去相关前，R很小，趋近于0，说明模糊度间存在较强的相关性；E很大，表明搜索椭球被拉得非常扁长，也反映了模糊度间的强相关。去相关后，R明显增大，接近于1，同时E大幅减小，协方差阵越接近于对角阵，各模糊度之间的相关性得到降低，说明本文算法具有较好的去相关效果，适合采用遗传算法搜索得到最优解。

设种群大小为20，最大进化代数为200[12]，利用本文的遗传算法对整周模糊度进行搜索和解算实验，仿真结果如图3所示。

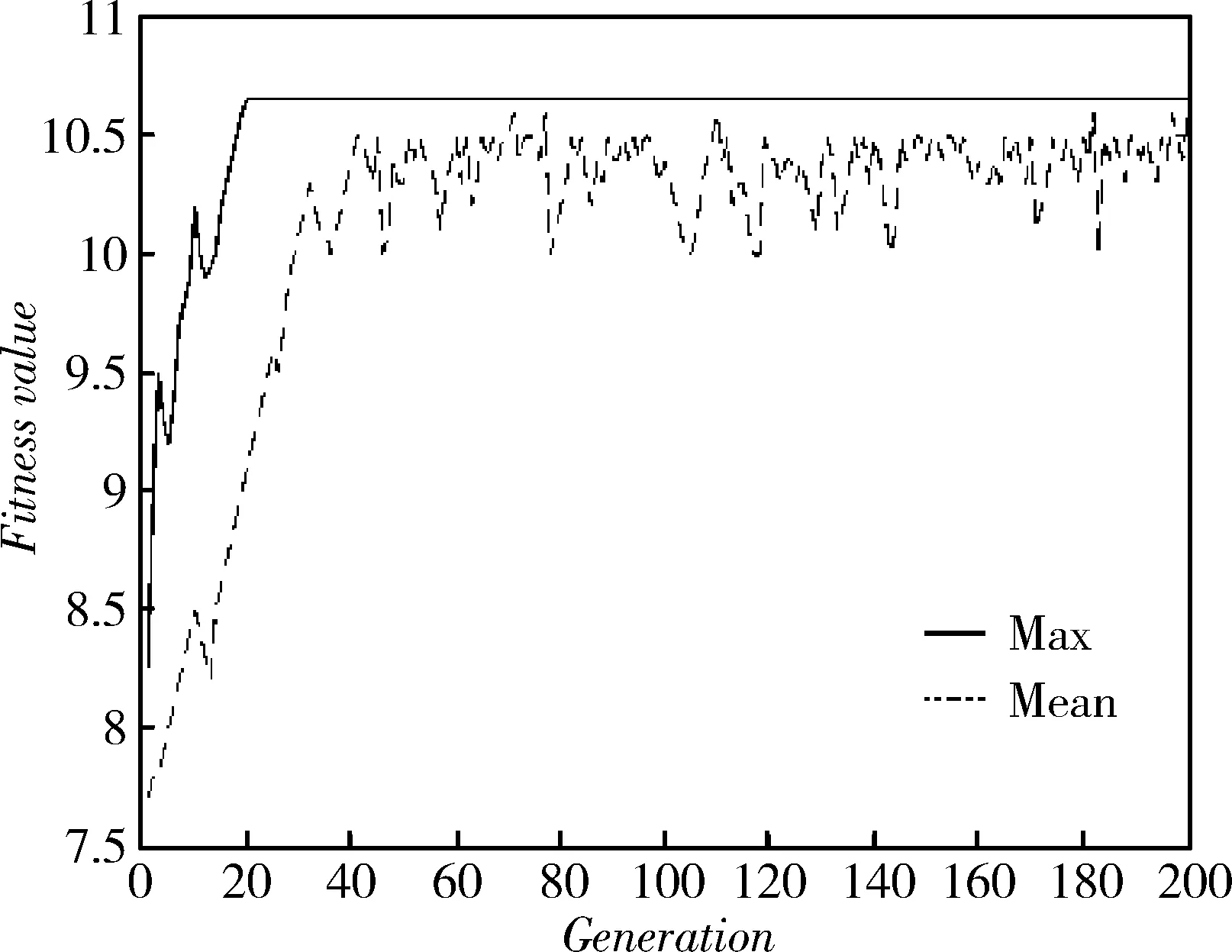
图3 仿真结果

由图3可知(横坐标表示进化代数，纵坐标表示群体适应度值),本文算法能搜索到正确的最优解,进化到算法终止子代时,只有极小部分的结果陷入局部最优解，且在20代以内就能收敛到全局最优解，即大部分的个体在20代以内就收敛了，而简单遗传算法[17]在第100代才收敛到最优值。取20代收敛，其搜索空间为400(20×20)，占问题空间(213)的4.3%，这表明本文算法在整周模糊度的寻优求解上具有较高的搜索效率。

在搜索到正确的整周模糊度值的前提下，Lambda算法和简单遗传算法[17]与本文算法用时如表2所示。

表2 3种算法用时对比分析结果

由表1可知，本文算法的用时明显少于Lambda法和简单遗传算法。这是因为Lambda是围绕某一初始浮点解开始搜索解算过程的，因此这一初始点的选择关乎整个搜索过程的效率。而单个点所能提供的搜索信息不多，当观测数据较多时，Lambda的搜索空间较大、计算也较为复杂且计算时间较长。在去相关过程中，Lambda采用的高斯分解也存在数值不稳定和运算量大的缺点。简单遗传算法的编码模式是二进制编码，汉明悬崖问题不可避免，且编码参数较多，而在遗传算子部分，恒定的交叉和变异概率等都大大影响了遗传算法的搜索效率。

4 结论

系统地研究了DGPS定位模型中整周模糊度的求解问题。在浮点解的求解过程中采用了卡尔曼滤波，在去相关的过程中采用了基于排序的Cholesky分解，最后在基线长度已知的情况下，基于实数编码，将自适应遗传算法引入到DGPS整周模糊度的搜索解算中。通过对算法的仿真分析和比较可知，本文算法的求解时间远小于Lambda算法，收敛速度远高于简单遗传算法，是一种高效的整周模糊度快速解算方法，对于实时动态定位技术的研究具有一定的参考意义。

[1] 刘经南.GNSS整周模糊度确认理论方法研究进展[J].武汉大学学报,2014,39(9):1009-1016.(Liu Jingnan.Review of GNSS Ambiguity Validation Theory[J].Geomatics and Information Science of Wuhan University,2014,39(9):1009-1016.)

[2] Teunissen P J G.The Least-squares Ambiguity Decorrelation Adjustment:A Method for Fast GPS Integer Ambiguity Estimation[J].Journal of Geodesy,1995,70(1-2):65-82.

[3] 邢喆.利用改进遗传算法求解整周模糊度[J].测绘科学,2011,36(3):110-113.(Xing Ji. Ambiguity Resolution Based on Improved Genetic Algorithm[J].Science of Surveying and Mapping,2011,36(3):110-113.)

[4] Teunissen P J G.The Invertible GPS Ambiguity Transformations[J].Manuscript Geodesy,1995,20(6):489-497.

[5] 李征航.GPS测量与数据处理[M].武汉:武汉大学出版社,2005:135-14.(Li Zhenghang.GPS Surveying and Data Processing [M].Wuhan:Wuhan University Press,2005:135-141.)

[6] Teunissen P J G.Integer Ambiguity Estimation with the Lambda Method[J].Proceedings of IEEE Symposium on Position Location and Navigation,1996,21(7):280-284.

[7] 刘经南.附有基线长度约束的单频数据单历元LAMBDA方法整周模糊度确定[J].武汉大学学报，2005,30(5):444-446.(Liu Jingnan. Ambiguity Resolution of Single Epoch Single Frequency Data with Baseline Length Constraint Using LAMBDA Algorithm [J]. Geomatics and Information Science of Wuhan University,2005,30(5):444-446.)

[8] Zhou Yangmei.A New Practical Approach to GNSS High-dimensional Ambiguity Decorrelation[J].GPS Solutions,2011,15(4):325-331.

[9] 黄张裕.一种改进的GPS模糊度白化滤波算法[J].西南交通大学学报,2010,45(1):150-155.(Huang Zhangyu. Modified GPS Ambiguity White-filtering Algorithm [J].Journal of Southwest Jiaotong University,2010,45(1):150-155.)

[10] Goldberg D E.Genetic Algorithms in Search Optimization and Machine Learning[M].New York:Addision Wesley,1989.

[11] 郑庆晖.基于遗传算法的整周模糊度OTF解算[J].国防科技大学学报,2001,23(3):12-17.(Zheng Qinghui.OTF Ambiguity Resolution Based on Genetic Algorithm[J].Journal of National University of Defense Technology,2001,23(3):12-17.)

[12] 王小平,曹立明.遗传算法-理论、应用与软件实现[M].西安:西安交通大学出版社,2002:18-38,73-74.(Wang Xiaoping, Cao Liming.Genetic Algorithm-Theory,Application and Software Implementation [M].Xi’an: Xi’an Jiaotong University Press,2002:18-38,73-74.)

[13] 夏传甲.基于实数编码遗传算法的GPS短基线整周模糊度搜索[J].大地测量与地球动力学，2012,32(1):136-140.(Xia Chuanjia.Integer Ambiguity Resolution of GPS Short-baseline Based on Real-coded Genetic Algorithm[J].Journal of Geodesy and Geodynamics,2012,32(1):136-140.)

[14] 刘经南.遗传算法解算GPS短基线整周模糊度的编码方法研究[J].武汉大学学报,2006,31(7):607-609.(Liu Jingnan. Ambiguity Resolution of GPS Short Baseline Using Genetic Algorithm[J].Geomatics and Information Science of Wuhan University,2006,31(7):607-609.)

[15] Srinvivas M,Patnaik L M. Adaptive Probabilities of Crossover and Mutations in Genetic Algorithms[J].IEEE Trans.on SMC,1994,24(4):656-667.

[16] Paul de Jonge.The LAMBDA Method for Integer Ambiguity Estimation:Implementation Aspects[J].Delft Geodetic Computing Center LGR Series,1996,12:1-49.

[17] 杨宁.遗传算法在DGPS动态整周模糊度解算中的应用[J].系统仿真学报,2005,17(8):2025-2026. (Yang Ning.Application of Genetic Algorithm in DGPS Integer Ambiguity Resolution[J].Journal of System Simulation,2005,17(8):2025-2026.)

Fast Integer Ambiguity Resolution Based on Real-Coded Adaptive Genetic Algorithm

Yi Qingming， Yi Xidong， Shi Min

School of Information Science and Technology, Jinan University, Guangzhou 510632, China

Aimingattheweakreal-timeperformanceinintegerambiguityresolution,anadaptivegeneticalgorithmbasedonreal-codingisproposedinthispaper.ThefloatsolutionofintegerambiguityiscalculatedbyapplyingKalmanfiltermethod,theorderingandmulti-time(inverse)pairedCholeskydecompositionareadoptedtodecorrelatethefloatsolutionanditscovariancematrix,Thus,thecorrelationofeachambiguityfloatestimationcanbeeliminated.Withthegivenbaseline,theintegerambiguitysearchspaceandtheintegerambiguityoptimizationresultscanbedeterminedbyusingadaptivegeneticalgorithmonthebasisofreal-coding.Thenumericalsimulationresultsshowthat,theintegerambiguitiescanberesolvedbyusingthisproposemethodinashortertimethanLambdamethod,andstrongerconvergentabilityisacquired,whichiscomparedwithsimplegeneticalgorithm.Itisproventhatthisalgorithmisefficientforfastintegerambiguityresolution.

Integerambiguity; Kalmanfilter; Choleskydecomposition;Real-coding;Adaptivegeneticalgorithm

*广东省科技计划资助项目(2015B090910001)；广州市科技计划资助项目(201604010007)

2016-11-02

易清明(1965-)，女，湖南岳阳人，博士，教授，主要从事卫星导航信号处理的教学与科研工作；易夕冬(1992-)，男，湖南岳阳人，硕士研究生，主要研究方向为卫星导航信号处理；石 敏(1977-)，女，湖北襄樊人，博士，副教授，主要从事多媒体技术和信息安全的教学与科研工作。

V556.1

A

1006-3242(2017)03-0014-05