强机动条件下的弹载深组合ARCKF滤波方法研究*

汪益平 陈 帅 赵 琛 屈新芬

1.南京理工大学自动化学院，南京 210094 2.中国工程物理研究院电子工程研究所，绵阳 621000

强机动条件下的弹载深组合ARCKF滤波方法研究*

汪益平1陈 帅1赵 琛1屈新芬2

1.南京理工大学自动化学院，南京 210094 2.中国工程物理研究院电子工程研究所，绵阳 621000

针对弹道导弹飞行中GNSS/SINS深组合导航系统呈现的强机动、非线性特性，引入了基于三阶球面-径向准则的容积卡尔曼(CKF)非线性滤波方法。同时，提出了一种自适应抗差容积卡尔曼滤波(ARCKF)算法，该算法运用抗差M思想，调节量测噪声阵，以抵御系统观测异常扰动，采用自适应因子对协方差阵进行调节，进一步处理动态扰动引入的误差。实验结果表明，该滤波算法有效提高了组合导航的动态性能，在加速度达到60g的强机动仿真环境中，仍能保持较高的导航精度和跟踪性能。 关键词 弹道导弹；深组合；强机动；ARCKF

强机动、高动态环境下对载体进行导航定位是一个热点和难点问题，在军事应用中的地位尤其重要，已被国内外众多学者广泛关注。强机动、高动态条件下的导航定位难点主要有：惯性导航系统解算误差变大，对定位技术也提出了很高的要求；系统观测传递函数为强非线性，线性化误差导致系统发散，因此，对GNSS/SINS组合导航系统的非线性系统估计和滤波问题的研究具有重要的理论意义[1]。

迄今为止，在非线性估计领域尚没有一种“最好”的算法，必须根据具体应用场合和条件，在适用性、估计精度及计算量等各种指标之间综合权衡。传统组合导航中的非线性滤波[2-3]一般采取扩展卡尔曼滤波(EKF)、无迹卡尔曼滤波(UKF)以及粒波容积卡尔曼滤波(CKF)[4-5]等。与EKF相比，CKF不需计算Jacobian矩阵，更适合非线性系统；同时，CKF克服了UKF在高维系中出现的数值不稳定及精度降低的问题，计算量较PF也更低。因此，非线性滤波CKF在组合导航中的应用具有一定的研究价值。

由于在强机动、高动态等复杂环境中，有可能给载体带来观测异常以及由动力学模型不准确导致的误差，本文在标准CKF算法基础上，运用抗差估计原理与构造自适应因子对标准CKF算法进行改进，提出一种自适应抗差容积卡尔曼滤波(ARCKF)[6]，以进一步提高组合导航滤波器性能。

1 GNSS/SINS深组合导航模型

与GNSS/SINS的松/紧组合相比，GNSS/ SINS深组合导航系统的显著特征是信息融合程度的进一步深入，涉及到GNSS接收机内部跟踪环路，形成GNSS与SINS相互辅助模式。

按照在深组合导航滤波中所用观测量的差异，可将深组合导航算法分为基于位置、速度组合的深组合导航算法，基于伪距、伪距率组合的深组合导航算法以及基于I/Q值的深组合导航算法。在本文弹载组合系统中，选取伪距、伪距率为观测量，以建立在发射惯性系下的GNSS/SINS深组合导航模型[7]。

1.1 深组合系统状态方程

1.1.1 SINS的误差状态方程

SINS的15×1维误差状态方程为：

XI=[φxφyφzδVxδVyδVzδX

(1)

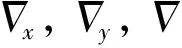
(2)

式中，FI(t)为SINS系统状态转移矩阵,GI(t)为SINS系统噪声驱动矩阵，wI(t)为SINS系统噪声矩阵。各矩阵具体形式见文献[8-9]。

1.1.2GNSS的误差状态方程

深组合系统中，GNSS接收机的误差状态量通常取为：与时钟频率误差等效的距离率误差Δlru与距离误差Δlu，其状态方程为：

(3)

式中，

(4)

(5)

式(2)和(3)即可构成发射惯性系下深组合导航系统的状态方程。

1.2 深组合系统观测方程

(6)

ρg=ρ+δlu+vρ

(7)

式中，δlu为GNSS的时钟误差引起的距离误差，vρ为伪距量测噪声。ρ与ρi可由下式计算：

(8)

(9)

式中，位置误差量δX，δY，δZ均可由式(1)中状态量滤波估计得出。将式(9)代入式(8)，即可得到理想距离ρ，则伪距率差非线性观测方程为：

δρ=ρi-ρg=ρi-ρ-δlu-vρ

(10)

同理，可推导出伪距率差非线性观测方程为：

(11)

2 基于ARCKF的组合滤波算法

2.1 标准CKF滤波

根据第1节实际所建立的状态模型线性、观测模型非线性的深组合模型，离散化后，得到：

(12)

式中，Xk,Zk分别为系统的状态向量与量测向量；Fk为状态转移矩阵，h(·)为系统非线性量测函数；wk，vk为互不相关的零均值高斯白噪声序列，且满足下列关系：

(13)

式中，Qk，Rk分别为系统状态噪声和量测噪声序列的协方差阵，是对称的非负定矩阵。

基于三阶球面-径向容积规则的CKF算法流程如下：

(1)滤波初始化

(14)

(15)

(2)时间更新

计算k-1时刻Cubature点：

(16)

(17)

状态一步预测：

(18)

(19)

(20)

(3)量测更新

计算用于量测更新的Cubatue点：

(21)

(22)

式中，Sk|k-1通过Pk|k-1的Cholesky分解得到。

通过量测方程传播Cubature点：

(23)

计算增益矩阵：

(24)

(25)

(26)

(27)

状态估计值：

(28)

(29)

2.2 自适应抗差CKF滤波算法

在正常环境中，标准CKF即可满足组合导航的精度需求。但当遭遇到强机动、高动态等较恶劣环境时，系统极有可能遭遇较大的观测异常误差和由于系统模型不准确导致的动力学误差。近年来，杨元喜等[11]中国学者建立了一种自适应抗差滤波理论，该方法在标准线性Kalman滤波中效果显著。延续此思路，针对高动态、强机动弹体运动情形下深组合导航系统，本文从抗差调节观测噪声、自适应因子调节协方差阵两步构造自适应抗差容积卡尔曼滤波。

2.2.1 抗差滤波算法

为抵制观测粗差的影响，需要实时调节观测噪声。在标准CKF基础上，对式(25)进行调整修正：

(30)

(31)

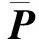
(32)

(33)

σvi=(Pyy,k|k-1)ii

(34)

(35)

抗差CKF算法是在标准CKF滤波方法的基础上，对噪声方差阵Rk进行在线修正，从而起到调节滤波增益阵，抵制导航系统观测粗差，抑制滤波发散的作用。以下对系统中的潜在动力学误差进行修正。

2.2.2 自适应抗差滤波算法

自适应滤波涉及到误差判别统计量以及自适应因子[12]。需要构造动力学模型误差学习统计量，即状态不符值统计量、预测残差统计量等，本文在2.2.1节中提出的抗差修正的基础上，使预测残差理论协方差矩阵等于或约等于估计的预测残差协方差矩阵，求出自适应因子，并修正一步预测协方差阵Pk|k-1，如下：

(36)

自适应因子αk由如下方法确定：

αk=

(37)

(38)

下面，总结自适应抗差CKF算法步骤：

1)由式(14)和(15)给定滤波初始值；

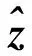
5)自适应调节一步预测协方差矩阵。由式(30)和式(36)～(38)完成对Pk|k-1的自适应调节。应注意：由式(37)得出自适应因子αk后进行判断，若αk值等于1，则进行标准CKF量测更新的余下步骤：式(26)～(29)，滤波结束；若αk值小于1，则进入步骤6)；

3 ARCKF仿真实验及结果分析

为了验证GNSS/SINS深组合导航中自适应抗差容积卡尔曼滤波器(ARCKF)的优越性，本文在开发的全软化仿真平台系统中进行深组合导航仿真实验，并与标准卡尔曼滤波(KF)效果进行比较。本实验系统由飞行轨迹发生器、卫星信号模拟器、软件接收机、惯导解算模块及组合模块等几个部分组成。仿真条件设置如下：弹体初始俯仰角为90°，初始滚转角和偏航角均为0°；初始姿态误差均设为0°；初始位置为：纬度31.98°，经度118.8°，高度0m；发射惯性坐标系下初始速度前向为394.8917m/s(地球自转速度)，天向和侧向均为0m/s；发射方位角为90°；60～68s间最大加速度达到60g，完全符合强机动、高动态特性。发射惯性系下超紧组合导航仿真系统的仿真参数设置如表1所示，得到的飞行轨迹如图1所示。

表1 仿真参数设置

图1 发射点惯性系下的飞行轨迹

图2 X方向速度误差

图3 Y方向速度误差

图4 Z方向速度误差

图2～4为X，Y，Z三个方向的速度误差对比图。由上述仿真结果可以看出，在非高动态时段，即在0～60s仿真时段，自适应抗差容积卡尔曼滤波(ARCKF)与卡尔曼滤波(KF)有较相似的仿真结果；在高动态时段60～68s，弹体加速度最高达到60g，观察KF滤波X，Y，Z三个方向的速度误差最大依次达到-1.5m/s，-0.25m/s，-1.1m/s；ARCKF滤波的X，Y，Z三个方向的速度误差依次为-0.7m/s，0.15m/s，-0.2m/s，误差绝对值均比KF误差要小，较KF滤波结果有一定改善。由此可证明，本文所提出的自适应抗差CKF算法有效提高了导航系统在高动态、强机动条件下的滤波性能。

4 结论

针对弹道导弹GNSS/SINS深组合导航系统的强机动、高动态特性，设计了一种适用于非线性系统的自适应抗差容积卡尔曼(ARCKF)组合导航滤波器。仿真结果表明，与卡尔曼滤波相比，该滤波方法在载体机动较强的情形下，具有更优越的鲁棒性能，进一步提高了组合导航在复杂环境中的跟踪性能与导航精度。

[1] 李子月. 高动态下GPS/SINS超紧组合导航系统研究[D]. 浙江大学, 2013. (Li Ziyue. The Research of Ultra-Tightly Coupled GPS/SINS Intergration System in High Dynamic Conditions [D]. Zhe Jiang University, 2013.)

[2] 王小旭,潘泉,黄鹤,等.非线性系统确定采样型滤波算法综述[J].控制与决策,2012, 6(27): 801-812. (Wang Xiaoxu, Pan Quan, Huang He, et al. Overview of Deterministic Sampling Filtering Algorithms for Nonlinear System[J]. Control and Decision, 2012, 6(27): 801-812.)

[3] 赵琳, 王小旭, 丁继成, 等. 组合导航系统非线性滤波算法综述[J]. 中国惯性技术学报, 2009, 17(1): 46-52. (Zhao Lin, Wang Xiaoxu, Ding Jicheng, et al. Overview of Nonlinear Filter Methods Applied in Integrated Navigation System[J]. Journal of Chinese Insertial Technology, 2009, 17(1): 46-52.)

[4] Arasaratnam I, Simon H. Cubature Kalman Filters[J]. IEEE Transactions on Automatic Control, 2009, 54(6): 1254-1269.

[5] Arasaratnam I, Simon H, Hurd T R. Cubature Kalman Filtering for Continuous Discrete Systems: Theory and Simulations[J]. IEEE Transactions on Signal Processing, 2010, 58(10): 4977-4993.

[6] 赵欣, 王仕成, 廖守亿, 等. 基于抗差自适应容积卡尔曼滤波的超紧耦合跟踪方法[J]. 自动化学报, 2014, 40(11): 2530-2540. (Zhao Xin, Wang Shicheng, Liao Shouyi, et al. An Ultra-tightly Coupled Tracking Method Based on Robust Adaptive Cubature Kalman Filter[J]. Acta Automation Sinica, 2014, 40(11): 2530-2540.)

[7] 杨洋. GPS/INS 深组合导航中关键技术研究[D]. 南京: 南京理工大学, 2013. (Yang Yang. Research on Key Technologies of SINS/GPS Deeply Coupled Navigation System [D]. Nanjing: Nanjing University of Science & Technology, 2013.)

[8] 董亮, 陈帅, 韩乃龙. 发射惯性系下GPS/SINS组合导航方法研究[J]. 电光与控制, 2016, 23(7):11-14. (Dong Liang, Chen Shuai, Han Nailong. GPS/SINS Integrated Navigation in Launch Inertial Coordinate System[J]. Electronics Opptics & Control, 2016, 23(7): 11-14.)

[9] 秦永元, 张洪钺, 汪叔华. 卡尔曼滤波与组合导航原理(第2版)[M]. 西安: 西北工业大学出版社, 2012. (Qin Yongyuan, Zhang Hongyue, Wang Shuhua. Kalman Filter and Integrated Navigation Principle (Second Edition)[M]. Xi’an:Northwestern Polytechnical University Press Lo. Ltd, 2012.)

[10] 王楠, 王龙. 惯性系下GPS/SINS紧组合导航算法研究[J]. 现代检测技术, 2011, 34(20): 93-96. (Wang Nan, Wang Long. Rrsearch of GPS/SINS Tightly Integrated Navigation Algorithm in Inertial Coordinate[J]. Modern Electronics Technique, 2011, 34(20): 93-96.)

[11] 杨元喜, 任夏, 许燕. 自适应抗差滤波理论及应用的主要进展[J]. 导航定位学报, 2013, 1(1): 9-15. (Yang Yuanxi, Ren Xia, Xu Yan. Main Progress of Adaptively Robust Filter with Applications in Navigation[J]. Journal of Navigation and Positioning, 2013, 1(1): 9-15.)

[12] 黄盼, 张晓, 藤云龙, 等. 基于AR-SRCKF的SINS/GPS深耦合抗转发式干扰研究[J]. 计算机工程与应用, 2016, 52(2): 31-35. (Huang Pan, Zhang Xiao, Teng Yunlong, et al. Research on Countermeasure for Repeater Jamming in Deeply Coupled SINS/GPS System Based on AR-SRCKF[J]. Computer Engineering and Applications, 2016, 52(2): 31-35.)

Research on the Method of Missile-loaded Deeply-Integrated ARCKF Filtering under Strong Maneuver

Wang Yiping1，Chen Shuai1， Zhao Chen1，Qu Xinfen2

1. School of Automation, Nanjing University of Science and Technology, Nanjing 210094, China 2. Institute of Electronic Engineering, China Academy of Engineering Physics, Mianyang 621000, China

AimingatthestrongmaneuveringandnonlinearcharacteristicsofGNSS/SINSdeeplyintegratednavigationsysteminballisticmissileflight,thecubatureKalmanfilter(CKF)basedonthird-degreespherical-radialcubatureruleisintroducedinthispaper.Meanwhile,anadaptiverobustcubatureKalmanfilter(ARCKF)isproposed.TherobustnessMisusedinthisalgorithmtoadjustthemeasurementnoisematrixtoresistsystemdisturbance,andtheadaptivefactorisusedtoadjustthecovariancematrixtofurtherdealwiththeerrorintroducedbythedynamicdisturbance.Theexperimentalresultsshowthatthedynamicperformanceofintegratednavigationsystemcanbeeffectivelyimprovedbyusingproposedalgorithm,andhighnavigationprecisionandtrackingperformancecanbemaintainedunderthestrongmaneuversimulationenvironmentwithaccelerationupto60g.

Ballisticmissile;Deeplyintegrated;Strongmaneuvering; ARCKF

*国家自然基金委员会和中国物理研究院联合基金资助(U1330133);中央高校基本科研业务费专项资金资助(30916011336);江苏博士后科研资助计划(1501050B);中国博士后基金(2015M580434);中国博士后特别资助(2016T90461)

2017-01-19

汪益平(1990-)，男，安徽池州人，硕士研究生，主要研究方向为组合导航；陈 帅(1980-)，男，江苏南通人，博士，副教授,硕士生导师，主要研究方向为导航、制导与控制；赵 琛(1991-)，男，湖北仙桃人，硕士研究生，主要研究方向为组合导航；屈新芬(1971-)，女，四川邻水人，博士，副研究员，主要研究方向为系统辨识、信息融合及惯性传感器研究和应用。

V249.3

A

1006-3242(2017)03-0003-06