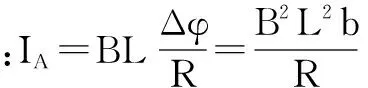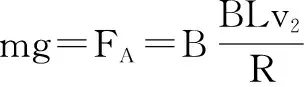应用动量定理分析电磁感应的两种方法

2017-07-21许文

数理化解题研究 2017年16期

关键词：动量定理安培力冲量

许文

(华中科技大学附属中学，湖北武汉 430074)

应用动量定理分析电磁感应的两种方法

许文

(华中科技大学附属中学，湖北武汉 430074)

导体棒做切割磁感线运动类电磁感应问题，导体受到的安培力往往随速度的变化而变化.在应用动量定理研究这类问题时，安培力的冲量求法是关键，本文探讨了微元法与推论法求安培力的冲量.

动量定理;电磁感应; 安培力冲量;方法

在导体棒或线圈做切割磁感线运动的这类电磁感应问题中，导体棒或线圈受到的安培力的大小FA往往与其运动速度的大小v有关.如果导体棒或线圈的运动是变速运动，则FA的大小是变化的，因此导体棒或线圈合受到的合外力一般也是变化的.我们在用动量定理求解这类电磁感应问题时，可以采用微元法与安培力冲量的推论两种方法.

一、微元法

微元法是分析、解决物理问题中的最基本的方法，它把研究对象或把物理过程分割为无限多个无限小的部分，然后抽取其中的一部分加以研究，来达到认识整体或全过程的性质和规律.微元法与动量定理相结合，是解决电磁感应中变力问题的一种有效方法.

例1 如图1所示，顶角θ= 45°的金属导轨MON固定在水平面内，导轨处在方向竖直、磁感应强度为B的匀强磁场中.一根与ON垂直的导体棒在水平外力作用下以恒定速度v0沿导轨MON向左滑动，导体棒的质量为m，导轨与导体棒单位长度的电阻均匀为r.导体棒与导轨接触点a和b，导体棒在滑动过程中始终保持与导轨良好接触.t=0时，导体棒位于顶角O处，求:(1)t时刻流过导体棒的电流强度I和电流方向； (2)导体棒作匀速直线运动时水平外力F的表达式； (3)导体棒在0～t时间内产生的焦耳热Q；(4)若在t0时刻将外力F撤去，导体棒最终在导轨上静止时的坐标x.

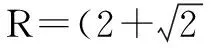
点评本题第(4)问棒在撤去外力后切割磁感线做非匀变速运动，回路中因存在感应电流，导体棒受到的安培力是一个变力，对于这类运动，我们一般不能运用牛顿运动定律与匀变速运动的规律进行求解.由于动量定理中合外力的冲量可以包含变力冲量的平均值，求这个变化安培力的平均冲量是用动量定理分析求解问题的难点.以上解法中采用了微元法.在一个“微元”的很短时间Δt或很小位移Δx内，非匀变速运动可以看作匀变速运动或匀速运动，于是有vΔt=Δx，lvΔt=ΔS.微元法体现了微分思想；然后在对ΔS求和的过程中又体现了积分思想.

例2 如图3所示，空间等间距分布着水平方向的条形匀强磁场，竖直方向磁场区域足够长，磁感应强度B=1 T，每一条形磁场区域的宽度及相邻条形磁场区域的间距均为d=0.5 m，现有一边长l=0.2 m、质量m=0.1 kg、电阻R=0.1Ω的正方形线框MNOP以v0=7 m/s的初速从左侧磁场边缘水平进入磁场，求:(1)线框从开始进入磁场到竖直下落的过程中产生的焦耳热Q；(2)线框能穿过的完整条形磁场区域个数n.

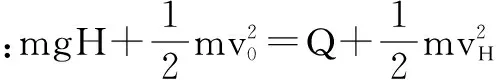
点评动量定量的表达式是一个矢量式，应用动量定理时应注意该定理的矢量性.本题中线圈在水平方向上受变化的安培力与竖直方向上重力的作用，其的运动情况较复杂.根据运动的合成与分解，我们将线圈的运动分解为水平方向上的非匀变速运动与竖直方向上的自由落体运动，在水平方向上应用动量定理求出线圈在磁场中受安培力作用时水平方向上运动的距离x，这是问题求解的关键.

二．安培力平均冲量的推论

此推论表明，变化的安培力FA的平均冲量大小IA可以通过一段时间内流过电路中的电量q或电路中磁通量的改变量Δφ来求出，从而为利用动量定理来定量分析研究这类电磁感应问题带来方便.

例3 如图5所示，两根光滑的平行金属导轨MN、PQ处于同一水平面上，相距L=0.5 m，导轨的左端用R=3Ω的电阻相连，导轨的电阻不计，导轨上跨接一电阻r=1Ω的金属杆，其质量m=0.2 kg，整个装置放在竖直向下的磁感应强度B=2 T的匀强磁场中.现对金属杆施加一水平向右的拉力F=2 N，使之由静止开始运动，求:

(1)金属杆运动的最大速度vm是多少？

(2)若已知金属杆从静止开始运动到最大速度的过程中，电阻R上共产生热量QR=10.2 J，此过程持续的时间t为多少？

(3)若金属杆达到最大速度后撤去拉力F，金属杆还能在导轨上滑行的距离x是多少？