排列组合问题中的数学思想
2017-07-21罗小平
罗小平
(江西省信丰中学,江西 赣州 341600))
排列组合问题中的数学思想
罗小平
(江西省信丰中学,江西 赣州 341600))
本文笔者通过几个排列组合问题的实例,在求解问题过程中渗透多种数学思想方法,既达到了解题的目的,又提高了读者的数学思维能力.值得大家学习与参考.
排列组合;数学思想;数学思维能力
一、函数与方程思想
函数与方程思想就是利用函数、方程的观点和方法来处理变量或未知数之间的关系,从而解决问题的一种思维方式.函数与方程思想体现了动与静、变量与常量的辩证统一.二项展开式的系数最值的求解,排列、组合的有关求值问题中,都蕴藏着丰富的函数与方程思想.
例1 已知f(x)=(1+x)m+(1+x)n(m,n∈N*)的展开式中的一次项的系数为19.
①求f(x)展开式中x2项的系数的最小值;
②当项系数最小时,求f(x)展开式中x7项的系数.
分析 本题在得到m,n的关系后可借助于二次函数知识解决.
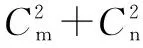
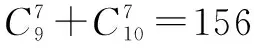
二、数形结合思想
数形结合的解题方法,就是把数学问题中的数量关系和几何图形结合起来考虑的思维方式.其实质就是将抽象的数学语言与直观的图形结合起来,抽象思维与形
象思维结合起来,使抽象问题具体化,复杂问题简单化,通过“数”与“形”的联系与转化,从而使问题得以解决.在解决有关排列问题时,如果能借助于图形进行数形结合,有时能使问题解决得简洁明快.
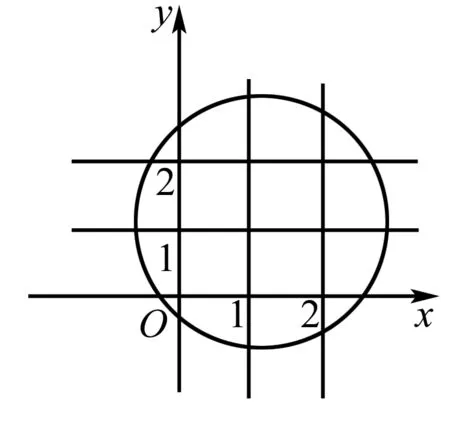
例2 以圆x2+y2-2x-2y-1=0内横坐标与纵坐标均为整数的点为顶点的三角形有多少个?
分析 利用坐标系,先求出圆内的整点个数,再求组合数.
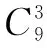
三、分类讨论思想
分类讨论是一种重要的解题策略,它体现的是化整为零,各个击破的思想.在解答数学题时,如果题目受到各种限制条件的制约,很难从整体上加以解决,这时就从分割入手,把整体划分为若干个局部,转而去解决局部问题,最后达到整体上的解决.在进行分类讨论时,一定要做到不重不漏.
例3 新学期开始,某学校新招聘了6名教师,要把他们按排到3个宿舍去,每个宿舍2人,其中甲必须在一号宿舍,乙与丙不能到三号宿舍,不同的安排方法有多少种?
分析 本题是有附加条件的组合问题,可先安排甲,然后对乙、丙进行分类,最后再安排其他人.
解 先安排甲到一号宿舍,然后安排乙.
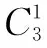
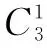
四、等价转化思想
等价转化就是在处理问题时,把待解决的问题或难解决的问题,通过某种转化过程,归结为一类已经解决或易解决的问题,最终求得问题的解答.有些排列组合问题,根据题目的结构特征,需要变换观察的视角,改变思考的路径,采用“倒过来想”,“正难则反”的逆向思维策略,以此来达到顺畅解题的目的.
例4 在2010年世博会期间,组织者要从6名男志愿者和4名女志愿者中选出4人,分别从事解说,接待,宣传,清洁工作.若这4人中至少有一名女志愿者,则选派方案共有多少种?
分析 本题直接求解,需要讨论女志愿者的人数,比较麻烦,而我们采用逆向思考的方法,可使问题简洁获解.
五、整体思想
整体思想是一种重要的数学思想方法,就是结合题目条件,把特殊的组合视为一个整体,通过整体代入来达到处理与解决问题的目的.在排列组合问题中,许多元素相邻,可按“整体思想”把相邻的元素视为一个元素,作为一个整体进行计算,然后再将相邻元素内部进行排列.
例5 让4对孪生兄弟排成一排,每对孪生兄弟不能分开,共有多少种排法?
分析 将每对孪生兄弟看成一个整体进行排列,然后内部再进行排列.
[1]洪其强.解排列组合问题中的数学思想[J].高中数理化,2009(Z1).
[责任编辑:杨惠民]
2017-05-01
罗小平(1975.11-),男,江西信丰人,高级教师,从事高中数学教育教学.
G632
B
1008-0333(2017)16-0008-02
