谈谈蜗牛爬井式运动模型
2017-07-21郭公礼
郭公礼,于 淼
(1.乌鲁木齐一中,乌鲁木齐 830006, 2.乌鲁木齐高级中学,乌鲁木齐 830049)
谈谈蜗牛爬井式运动模型
郭公礼1,于 淼2
(1.乌鲁木齐一中,乌鲁木齐 830006, 2.乌鲁木齐高级中学,乌鲁木齐 830049)
通过对直线运动式蜗牛爬井模型和回旋式蜗牛爬井模型的分析,强调运动过程认识,探究运动的细节处理,更好掌握此类题型解题规律及变式应用.
蜗牛;爬井;模型
小学数学有这样一道有趣的应用题:一口枯井十米深,一只蜗牛从井底向上爬,白天爬三米,晚上退两米,问几天能爬到井口?不少学生顺口就说十天,而答案是八天,像这样的运动,称之为“蜗牛爬井式”的运动模型,这类试题的运动特点学生模型不熟,过程不清,细节易错.对这类试题做一些题型的归类与梳理总结一下易错细节 ,探究一下解题规律,可以帮助学生更好的解决这类问题.
模型一:直线运动式的蜗牛爬井
这类试题的特点是:先正向直线运动X1的距离,再反向运动距离X2的距离,一个周期运动了(X1-X2),但题目中所给时间往往不是运动周期的整数倍,所以计算距离时有N(X1-X2)+△X其中△X需要单独处理,有时题目运动距离看似是(X1-X2)的整数倍,由于最后一段的正向运动的距离大于反向运动的距离,到达终点后无需返回,所以运动时间也不是周期的整数倍即N(t1-t2)+△t其中△t需要分段处理.体现了运动的共性与个性差异化处理模式.
例1 (动力学类)一个质量为2.0kg的物块放置光滑的水平面上,用一大小等于2N的力作用在物体上,1.5秒后撤去此力,用大小相等方向相反的力再作用2秒,以后每个2秒改变一次力的方向,共作用100秒,求通过的位移以及第一次运动50m的位移所用的时间.

图1
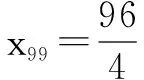
点评 本题的第二问易错点在于运动的位移恰好是运动一个周期位移的整数倍,学生容易误认为时间是运动周期的整数倍.实际上最后一段正向运动就达到了终点,不需反向运动就到达终点.
例2 (电场类)如图2(a)所示,两平行正对的金属板A、B间加有如图(b)所示的交变电压,一重力可忽略不计的带正电粒子被固定在两板的正中间P处.若在t0时刻释放该粒子,粒子会时而向A板运动,时而向B板运动,并最终打在A板上.则t0可能属于的时间段是( ).
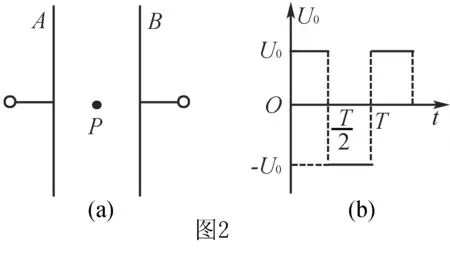

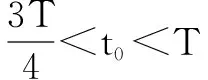
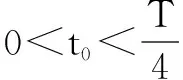
点评 粒子在电场中运动与动力学类似,但往往是采用逆向的命题,运到的模型题目已交代清楚,进入电场时刻不同,运动的模型与过程就不同,以四分之一周期为分界线,如正向运动的时间大于反向运动的时间,最终物体朝正向运动;反之则最终朝反方向运动.

例3 (动量类)如图3所示,水平传送带AB长l=8.3m,质量为M=1kg的木块随传送带一起以v1=2m/s的速度向左匀速运动(传送带的传送速度恒定),木块与传送带间的动摩擦因数μ=0.5.当木块运动至最左端A点时,一颗质量为m=20g的子弹以v0=300m/s水平向右的速度正对射入木块并穿出,穿出速度u=50m/s,以后每隔1s就有一颗子弹射向木块,设子弹射穿木块的时间极短,且每次射入点各不相同,g取10m/s2.求:
(1)在被第二颗子弹击中前,木块向右运动离A点的最大距离?
(2)木块在传送带上最多能被多少颗子弹击中?
(3)从第一颗子弹射中木块到木块最终离开传送带的过程中,子弹、木块和传送带这一系统所产生的热能是多少?(g取10m/s2)
解 (1)第一颗子弹射入木块过程中动量守恒mv0-Mv1=mu+Mv1′ (1)
解得:v1′=3 m/s (2)
木块向右作减速运动

解得t1=0.6 s/1 s(5)
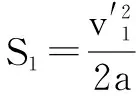
解得t1=0.6 s<1 s(6)
(2)在第二颗子弹射中木块前,木块再向左作加速运动,时间t2=1 s-0.6 s=0.4 s(7)
速度增大为v2=at2=2 m/s(恰与传递带同速)(8)
所以两颗子弹射中木块的时间间隔内,木块总位移S0=S1-S2=0.5m方向向右 (10)
第16颗子弹击中前,木块向右移动的位移为S=15S0=7.5m(11)
第16颗子弹击中后,木块将会再向右先移动0.9m,总位移为0.9m+7.5=8.4m>8.3m木块将从B端落下.所以木块在传送带上最多能被16颗子弹击中.
木块向右减速运动过程中板对传送带的位移为S′=v1·t1+S1(13)
产生的热量为Q2=μmgS′(14)
木块向左加速运动过程中相对传送带的位移为S′=v1·t1-S2(15)
产生的热量为Q3=μmgS′(16)
第16颗子弹射入后木块滑行时间为t3有
解得t3=0.4 s (18)
木块与传送带的相对位移为S=v1t3+0.8m(19)
产生的热量为Q4=μmgS(20)
全过程中产生的热量为Q=15(Q1+Q2+Q3)+Q1+Q4
解得Q=14155.5J(21)
点评 本题难点在于全程产生的热量要细分为:子弹打击木块生热,正向运动的摩擦生热,反向运动的摩擦生热,前15个子弹具有共性;即最后一发单独分段处理.
模型二:回旋式蜗牛爬井
这类试题的特点是:先正向旋进X1的距离,再反向旋进X2的距离,一个周期运动了(X1-X2),最后到达终点的距离为N(X1-X2)+X1距离(其中N为运动周期的整数倍),抓住这一点就抓住了解题的关键.
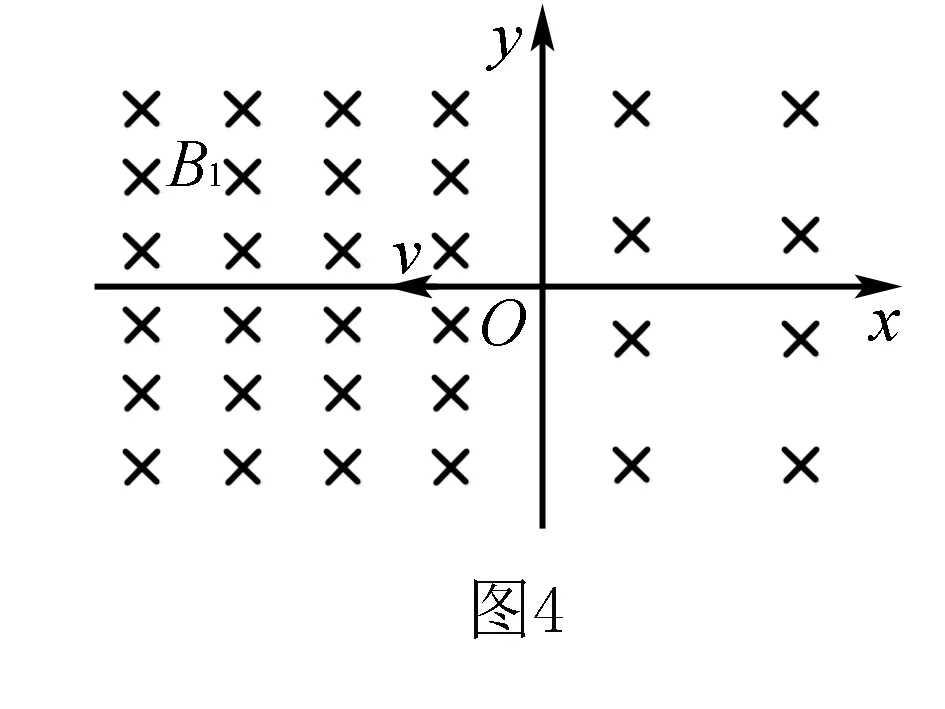
例4 (磁场类)如图4所示,在x<0与x>0的区域中,存在磁感应强度大小分别为B1与B2的匀强磁场,磁场方向均垂直于纸面向里,且B1>B2.一个带负电荷的粒子从坐标原点O以速度V沿x轴负方向射出,要使该粒子经过一段时间后又经过O点,B1与B2的比值应满足什么条件?
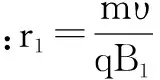

现分析粒子运动的轨迹.如图5所示,在xy平面内,粒子先沿半径为r1的半圆C1运动至y轴上离O点距离为2r1的A点,接着沿半径为r2的半圆D1运动至O1点,OO1的距离:d=2(r2-r1)(3)
此后,粒子每经历一次“回旋”(即从y轴出发沿半径为r1的半圆和半径为r2的半圆回到原点下方的y轴),粒子的y坐标就减小d.设粒子经过n次回旋后与y轴交于on点,若oon即nd满足:nd=2r1(4)
则粒子再经过半圆Cn+1就能经过原点,式中n=1,2,3,…为回旋次数.
联(1)(2)(5)式可得B1、B2应满足的条件:
点评 本题的难点一定要考虑粒子运动的周期性,许多学生没有写出表达的通式,只考虑了一种情况,造成漏解.
例5 (碰撞类)如图6,在x轴下方有匀强磁场,磁感应强度大小为B,方向垂直于xy平面向外.P是y轴上距原点为h的一点,N0为x轴上距原点为a的一点.A是一块平行于x轴的挡板,与x轴的距离为h/2,A的中点在y轴上,长度略小于a/2.带电粒子与挡板碰撞前后,x方向的分速度不变,y方向的分速度反向、大小不变.质量为m,电荷量为q(q>0)的粒子从P点瞄准N0点入射,最 后又通过P点.不计重力.求粒子入射速度的所有可能值.
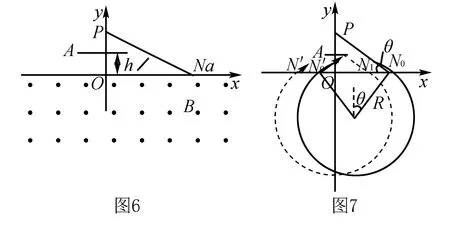
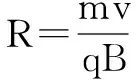
粒子速率不变,每次进入磁场与射出磁场位置间距离x1持不变有x1=N0′N0=2Rsinθ(2)
粒子射出磁场与下一次进入磁场位置间的距离x2始终不变,与N0′N1相等.由图可以看出x2=a(3)
设粒子最终离开磁场时,与档板相碰n次(n=0、1、2、3…).若粒子能回到P点,由对称性,出射点的x坐标应为-a,即(n+1)x1-nx2=2a(4)
联立(3)(4)(6)得n<3(7)
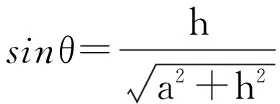
点评 本题的难点一是找到运动的表达通式,二是根据题目给定的特定条件(对称和边界)写出满足的临界条件的关系式.
总之,蜗牛爬井式运动试题既具有周期性的共性特性,最后一段的处理又各具特点,应引起足够的重视.
[1]教育部考试中心.普通高等学校招生全国统一考试大纲的说明[M].高等教育出版社,2012.
[责任编辑:闫久毅]
2017-05-01
郭公礼,男,乌鲁木齐市,高级教师,新疆奥赛特级辅导员,从事高中物理教育.
G632
B
1008-0333(2017)16-0063-03
