解析构造圆解最值问题

孙筱麟

(浙江省嵊州市马寅初中学高中部，浙江 杭州 312400)



解析构造圆解最值问题

孙筱麟

(浙江省嵊州市马寅初中学高中部，浙江 杭州 312400)

本文主要谈谈如何构造圆求解最大值和最小值问题，供师生参考.

构造圆；最大值；最小值

求最大值和最小值的方法较多，也各有特色，但构造法却非常新颖.

一、最大值问题

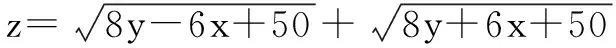
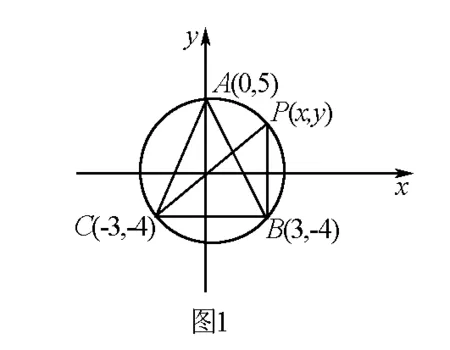
则z可以看成圆x2+y2=25上的点P(x,y)到这圆上两定点B(3，-4)，C(-3，-4)的距离之和，这个和最大时，显然P点在优孤中点.

解 如图1，∠ABC=∠ACB=α, ∠ABP=∠ACP=β,则AB=AC=2Rsinα,∴AB+AC=4Rsinα.又PC=2Rsin(α+β),PB=2Rsin(α-β).

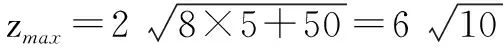
注：当β=0时，P(x,y)与A(0，5)重合.这时y=5,x=0.

二、最小值问题

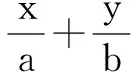
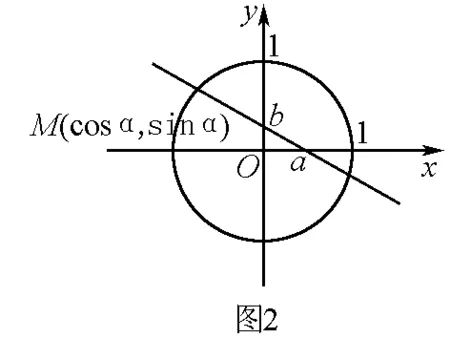
与圆x2+y2=1有公共点，即直线与圆相交或相切，故形如t=|ax+by+c|的最值问题，可转化为圆心到定直线距离的最值问题.

解 如图2构造一个辅助圆x2+y2=1，注意到M(cosα,sinα)恒在此圆上，由题意知直线恒过单位圆上一点M，即直线与辅助圆的关系为相切或相交.有圆心到直线距离d=

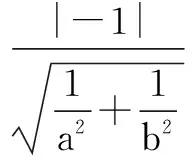
评注 此法的关键是根据点的特征联想到单位圆上的点，深入探究隐含条件，巧妙构造单位圆，问题转化为直线与圆的位置关系.

三、最大(小)值问题

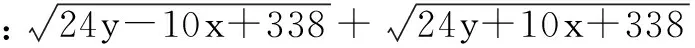
分析 由x2+y2=169,把所求式子变形

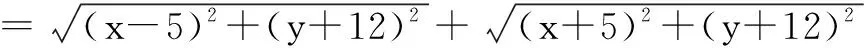
解 如图3，设P(x,y),A(5,-12),B(-5,-12)，

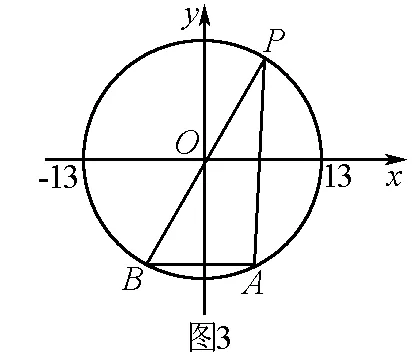
则所求式子M为圆x2+y2=169上一点到两定点A、B的距离的之和，即M=|PA|+|PB|.

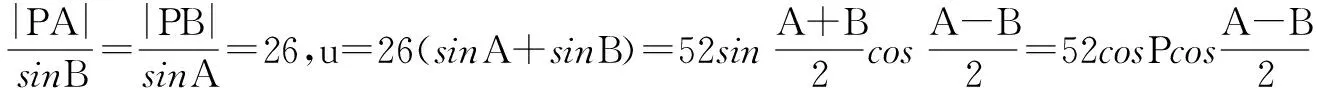
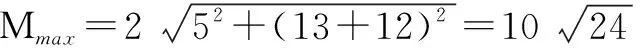
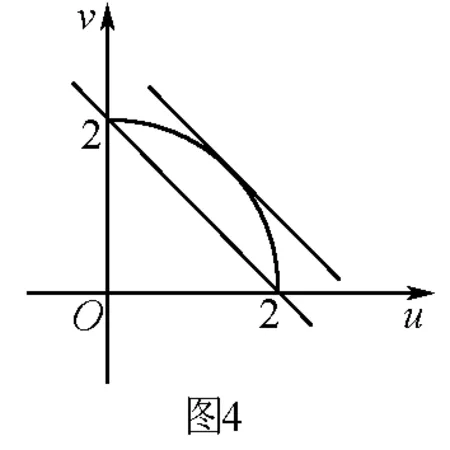
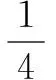
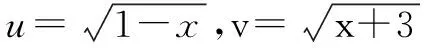
综上所述，应用构造圆求最大(小)值问题，关键在于根据题设及所求题目的结构特征去构造相适应的圆形求解即可.此法数形结合，直观性强，故便于理解，因此有必要一读.

[1]郑毓信.“数学文化”与数学教育[J].中学数学教学参考，2005(10).

[责任编辑：杨惠民]

2017-05-01

孙筱麟，男，2001，浙江嵊州人，浙江省嵊州马寅初中学高一年级.

G632

B

1008-0333(2017)16-0048-02