基于性能的平面不规则结构地震易损性分析

黄小宁，杜永峰, 2，李慧, 2



基于性能的平面不规则结构地震易损性分析

黄小宁1，杜永峰1, 2，李慧1, 2

(1. 兰州理工大学防震减灾研究所，甘肃兰州，730050；2. 兰州理工大学西部土木工程防灾减灾教育部工程研究中心，甘肃兰州，730050)

针对平面不规则框剪结构，提出基于性能的结构整体地震易损性分析方法。基于性能分析静力弹塑性，根据结构极限损伤状态定义平面不规则框剪结构层间位移角和层间扭转角的4个性能水平限值。通过弹塑性动力时程分析获得结构地震响应。根据超越概率的定义，分别计算层间位移角和层间扭转角极限状态下超越概率。结合地震峰值加速度及超越概率对一平面不规则框剪结构进行基于性能的地震易损性分析，绘制结构的易损性曲线，比较2个指标的易损性曲线，评估结构的抗震性能。研究结果表明：对平面不规则结构进行易损性分析时，应考虑扭转响应对结构的影响，防止高估这类结构的抗震性能。

平面不规则框剪结构；层间位移角；层间扭转角；性能水平；地震需求分析；易损性曲线

地震易损性分析可以预测结构在不同等级地震作用下发生各级破坏的概率，设计人员可以根据结构易损性的不同，有针对性地提高结构的抗震能力，从而尽可能避免或减少人员伤亡，实现我国防震减灾的目标。国内外对钢筋混凝土结构的易损性进行了大量的研究，取得了许多成果。刘晶波等[1−2]提出了一种基于性能的结构整体地震易损性分析方法，该方法既考虑了结构本身的不确定性，又考虑了地震动输入的不确定性，可全面评估地震灾害的损失。何益斌等[3]考虑地震动输入的不确定性，结合性能水平限值提出能有效评估结构地震响应的易损性分析方法。CIMELLARO等[4]提出了以加速度和层间位移为指标的基于多维性能极限状态结构的易损性分析方法。郑山锁等[5]基于传统IDA方法，采用拉丁超立方体网络抽样法考虑地震动强度及地震动入射角对结构的共同影响，提出了基于多元增量动力时程分析(MIDA)的地震易损性分析方法。以上方法均没有考虑扭转响应对结构易损性的影响。对于平面不规则结构而言，在地震过程中，作用在结构质心处的惯性力会对刚心产生扭转力矩，地震动的转动分量也会对结构产生扭转力矩，各种因素使结构产生不可忽略扭转响应。因此，在对平面不规则结构进行易损性分析时，有必要考虑扭转响应的影响。为此，本文作者首先通过基于性能的静力弹塑性分析方法，给出结构层间位移角4个极限损伤状态性能水平限值，推导层间位移角与层间扭转角之间的关系，得到层间扭转角4个极限损伤状态性能水平限值。最后，对平面不规则框剪结构进行基于性能的地震易损性分析，得到结构的易损性曲线，对该结构在不同强度地震作用下的破坏状态进行评估和分析。

1 地震易损性分析方法

抗震性能目标是地震设防水准和结构性能水平的函数，地震设防水准是带有一定概率保证率的地震动强度参数，结构性能水平是与每一级地震设防水准相对应的期望的结构最大损伤程度[6]。结构易损性定义为遭受特定外部作用下结构响应超越其极限损伤状态性能水平限值的概率[7]，因此，可以将性能设计理论应用于结构的地震易损性分析中。在perform-3D中建立合理的平面不规则框剪结构有限元模型进行静力弹塑性分析，确定以结构层间位移角、层间扭转角作为结构整体性能指标的结构性能水平限值，考虑地震动不确定性，对结构进行弹塑性动力时程分析。由于结构地震需求与抗震能力均服从对数正态分布，因此，可以利用对数正态分布的概率密度函数计算结构在不同强度地震动作用下的条件失效概率，并绘制对应不同地震动强度参数的地震易损性曲线。易损性分析流程如图1所示。

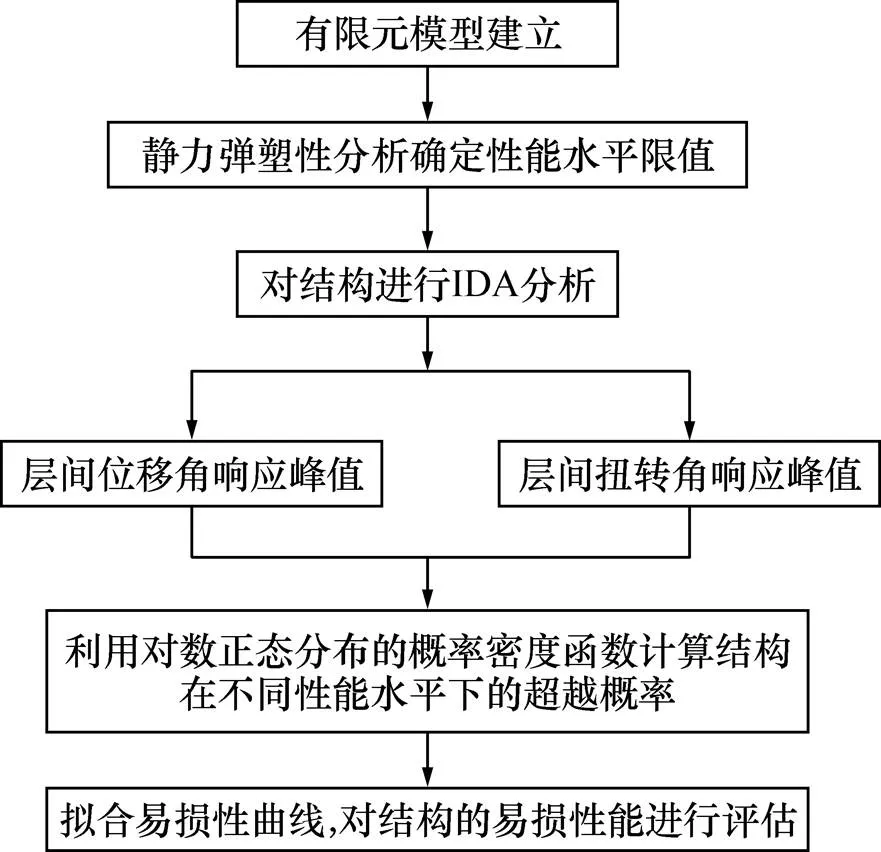
图1 结构地震易损性分析流程

2 计算模型

本文以1个平面不规则框架−剪力墙结构为例，该结构的抗震设防类别为乙类，抗震设防烈度8度(0.2)，设计地震分组第3组，场地类别Ⅱ类，结构形式为钢筋混凝土框剪结构，第8层层高5.4 m，其余层均为3.9 m，为了满足使用功能要求在第8层中去掉中间用方框标出的6根柱子，平面图如图2所示。楼板钢筋为HPB235；梁、柱主筋为HRB335，箍筋为HPB235；剪力墙主筋为HRB400，分布筋为HRB335。A-B轴处剪力墙厚为400 mm，其余剪力墙厚均为 300 mm，梁采用长×宽为700 mm×300 mm的截面，楼板厚100 mm，结构其余参数如表1所示。利用perform-3D对结构进行静力弹塑性分析及非线性时程分析时，剪力墙选用非弹性纤维截面，梁选用(FAMA Beam, Concrete Type)，柱选用(FAMA Column, Concrete Type)来模拟构件的非线性行为。

数据单位：mm

表1 极限破坏状态定义与对应量化性能指标限值[11]

3 结构极限损伤状态性能水平限值的确定方法

3.1 性能水平与量化指标

结构的抗震性能水平是一种有限的破坏状态，而且它与不同强度地震下结构期望的最大破坏程度相对应。参照国内外相关文献[8−9]中关于结构性能水平的划分，将结构的抗震性能水平划分为正常使用、立即使用、生命安全和防止倒塌4个性能水平。结构损伤状态的定义对易损性曲线形成起着至关重要的作用，直接影响易损性曲线的形状。我国GB 50011—2011“建筑抗震设计规范”[10]中划分了地震破坏分级且对各个破坏状态、继续使用的可能性及变形参考值进行了说明。为了将性能水平与地震破坏分级相对应，将基本完好的极限破坏状态定义为正常使用极限状态，将轻微损坏的极限破坏状态定义为立即使用极限状态，将中等破坏的极限破坏状态定义为生命安全极限状态，将严重破坏的极限破坏状态定义为防止倒塌极限状态。结合文献[1]及GB 50011—2011“建筑抗震设计规范”，设置框剪结构4个极限破坏状态的定义以及对应量化性能指标限值(见表1)。

3.2 量化指标限值的确定

刘晶波等[1]建议采用第一振型的倒三角侧向力分布形式对结构进行静力弹塑性分析，得到结构各性能点对应的性能目标的限值，但文献[11]建议对于平面不规则结构应沿2个方向同时推覆，本文考虑采用前两阶振型沿向和向同时推覆，并取柔性端作为结构的监测点。在进行分析时非约束混凝土的采用GB 50011—2011“混凝土结构设计规范”[10]中单轴应力应变关系的本构模型，钢筋采用有屈服点钢筋的本构模型，约束混凝土采用Mander本构模型[11]。

对结构进行Pushover分析，根据结果分别绘制向和向每层层间位移角与层剪力的关系曲线，然后根据楼层的极限破坏状态来确定不同性能水平层间位移角的限值，选取最小层间位移角限值作为结构整体性能水平层间位移角限值。图3所示为向最小层间位移角与层剪力的关系曲线，表2所示为层间位移角量化指标限值。

将表2中的结果与层间位移角参考值[10]对比可知，NO对应的层间位移角量化指标限值为1/833，与规范中1/800限值的要求基本相符。IO 对应的层间位移角限值为1/426，满足1/533~1/400的要求，此时少量的连梁及框架梁进入塑性阶段，说明已经发生一定程度的损伤，可以满足规范轻微损坏的性能水准。LF对应的层间位移角限值约1/208，满足1/267~1/200的要求，此时底层剪力墙、多数连梁和框架梁进入塑性阶段，但框架柱保持弹性完好的状态。CP对应的层间位移角限值为1/106，基本满足1/110限值的要求，此时剪力墙已经发生严重破坏，框架柱开始出现塑性铰。

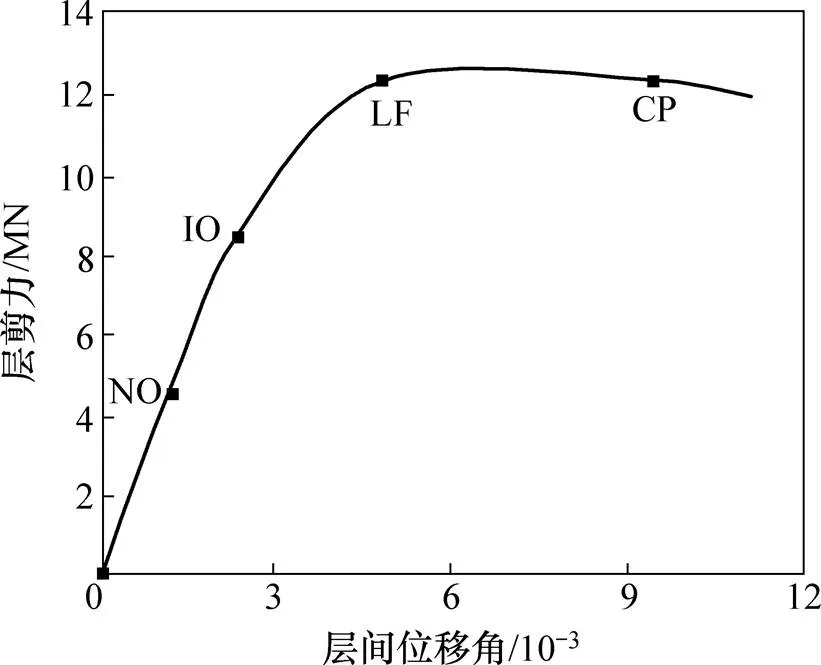
图3 结构能力曲线及性能水平限值

表2 层间位移角量化指标限值

根据层间扭转角与层间位移角之间的关系得到层间扭转角的限值。根据扭转不规则结构的相关定义[10]可知：

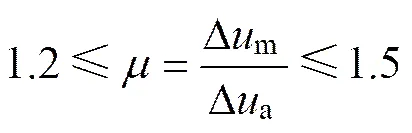
式中：Δm为最大层间位移；Δa为平均层间位移；为扭转位移比。

假定楼层最大层间位移可用下式表示[12]：

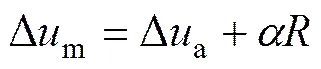
式中：为层间扭转角；为构件到结构刚心的最大距离。

假定层间平均位移Δa为

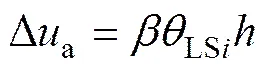
式中：为层高；LSi为第个性能水平下层间位移角度限值；为系数，＜1。

将式(2)和式(3)代入式(1)推导可得

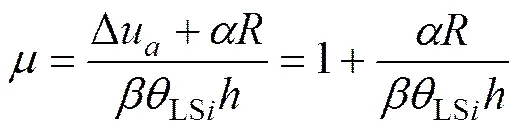
层间位移最大值必须满足

(5)

(6)

由式(4)和式(6)推导可知

将式(7)代入式(4)可得到层间扭转角与层间位移角限值之间的关系：

(8)

从式(8)可以看出，和是得到层间扭转角限值的关键，确定每一层刚心的位置就可求得。为最大层间位移与平均层间位移的比值，而在pushover分析过程中，求出层间位移角限值对应时刻的比较困难，本文利用钱稼茹等[13]推荐的推算平面端部位移法计算结构的扭转位移比。根据计算得到=1.32，根据式(1)对扭转位移比的规定可知该结构为平面不规则结构，将=1.32代入式(8)，层间扭转角的限值如表3所示。

表3 层间扭转角量化指标

4 结构的概率地震需求分析

4.1 结构的模态频率及地震动随机性

在地震作用下结构反映的主要与地震动的不确定性及结构的频率相关，本文根据结构的前3阶模态的自振频率(前3阶模态频率分别为1.26，1.41和2.17)及ATC-63建议的地震动记录，选择20条地震动调幅和8个地震波峰值加速度()(0.05，0.10，0.20，0.30，0.40，0.50，0.60，0.70，1=9.8 m/s2)作为地震激励。阻尼比为5%的20条地震记录的弹性加速度反应谱的离散性反映了地震动的偶然不确定性。

4.2 结构的概率地震需求分析

将所选择的20条地震波的峰值加速度按比例调整。通过增量动力时程分析(IDA)可知，第8层的向的层间位移角比其他层的大。因此，下面以第8层沿向的易损性曲线作为基础展开讨论，利用perform-3D软件进行分析后，得到以峰值加速度为变量的结构层间位移角、层间扭转角数据点[14−15]，如图4和图5所示。

1—NO；2—IO；3—LF；4—CP。

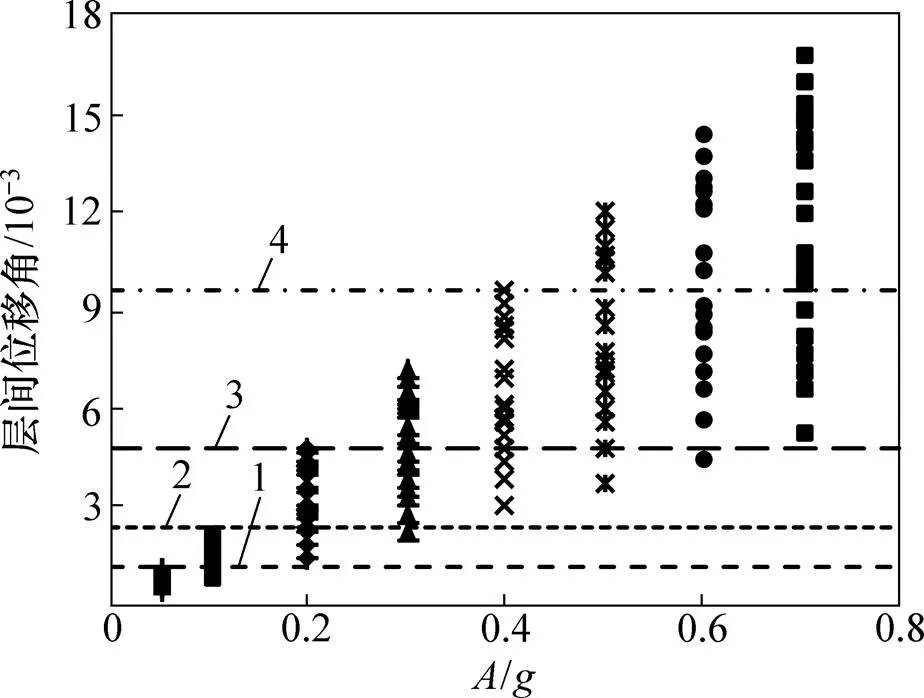
1—NO；2—IO；3—LF；4—CP。

图4中每列竖向数据点为不同地震波相同PGA下结构的层间位移角响应，横线从下向上依次代表了结构不同性能水平限值，具体取值与表2中结构的量化指标限值相对应。图5中每列竖向数据点为不同地震波相同PGA下结构的层间扭转角响应，横线从下向上依次代表了结构不同性能水平限值，具体取值与表3中结构的量化指标限值相对应。

4.3 易损性曲线的形成

根据本文对结构性能水平的定义和结构地震需求的概率分布，可以由式(9)求得不同PGA下结构需求超过限值的概率[16]，以层间位移角为例。

以层间位移角为指标的超越概率计算方法如式(9)所示，结合图4中得到的地震响应，可以得到不同PGA下结构需求超过性能水平限值的概率，以超越概率为纵坐标，以PGA为横坐标绘制以层间位移角为指标的易损性曲线，如图6所示。

从图6可以看出，结构正常使用极限状态的易损性曲线最为陡峭，说明结构在地震作用下超越正常使用性能水平的概率较大。随着结构从基本完好发展到倒塌状态，结构的易损性曲线逐渐变的扁平，即超越概率变越来越小，这是符合结构设计准则的。

采用上述方法也可得到以层间扭转角为指标的结构地震易损性曲线，图7所示为以层间扭转角为指标和以层间位移角为指标结构易损性曲线的比较。

从图7可以看出：以层间扭转角为指标的易损性曲线高于以层间位移角为指标的易损性曲线，说明结构以层间扭转角为指标时超过其性能水平限值的概率更大；在相同PGA下，结构更可能会因为扭转振动而产生破坏，以层间扭转角为指标对结构的抗震性能评估更为保守。

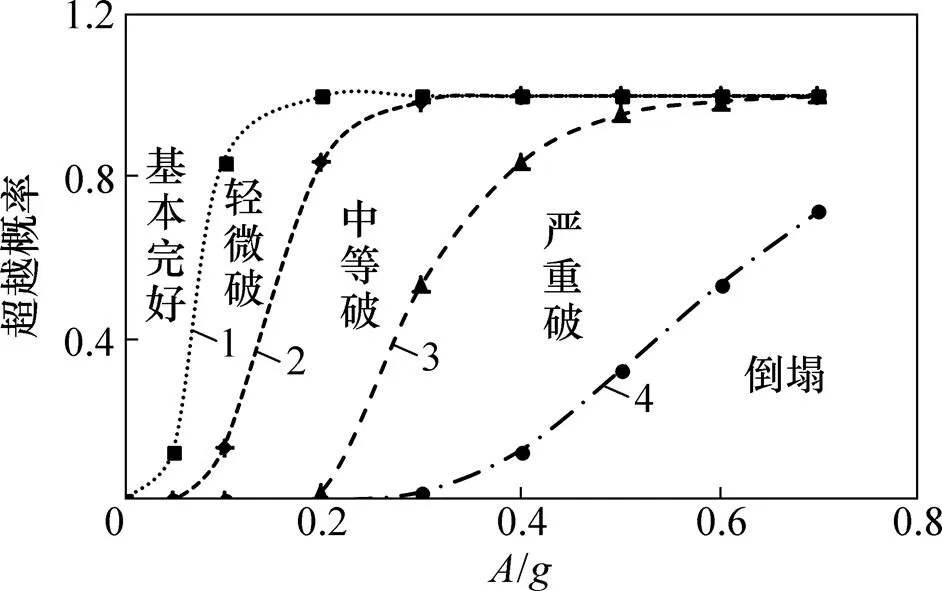
1—NO；2—IO；3—LF；4—CP。

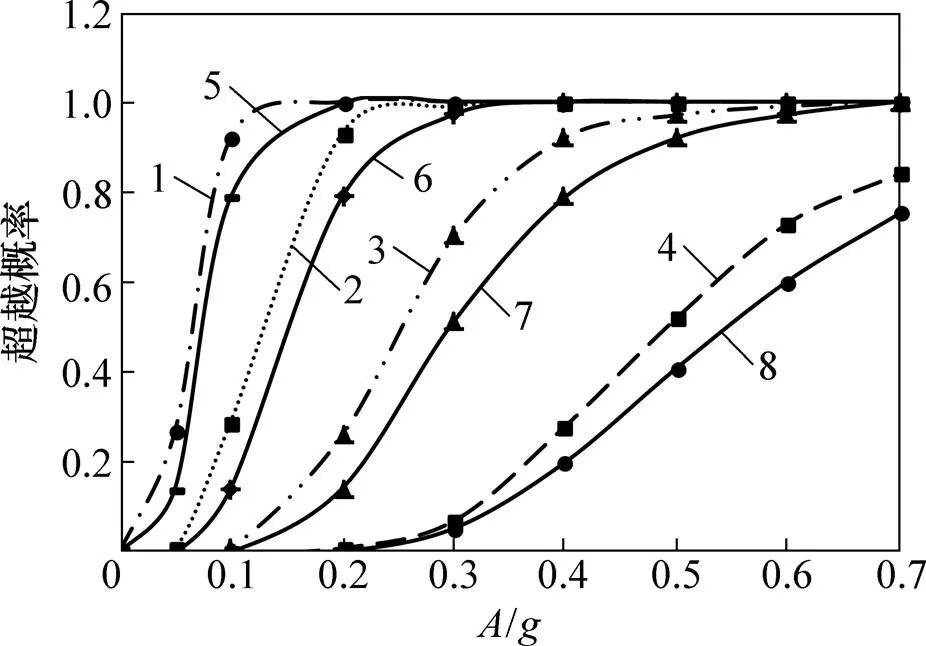
1—层间扭转角NO；2—层间扭转角IO；3—层间扭转角LF；4—层间扭转角CP；5—层间位移角NO；6—层间位移角IO；7—层间位角LF；8—层间位移角CP。

5 结论

1) 由结构极限损伤状态确定的层间位移角的4个性能水平限值，与GB50011—2010“建筑抗震设计规范”中给定的层间位移角限值的参考值基本相符。

2) 对于平面不规则结构，也就是当结构的扭转位移比大于1.2，进行易损性分析时不仅要以层间位移角为性能指标，考虑结构因平动产生的破坏，也要以层间扭转角为性能指标，考虑结构因扭转产生的破坏，防止高估这类结构的抗震性能。

3) 文中仅分析了分别考虑以层间位移角为性能指标和以层间扭转角为性能指标的结构地震易损性，但平面不规则结构可能会因为扭转与平动响应的同时作用而产生破坏，当同时考虑以层间扭转角和层间位移角为指标的地震易损性分析时需进一步研究。

[1] 刘晶波, 刘阳冰, 闫秋实, 等. 基于性能的方钢管混凝土框架结构地震易损性分析[J]. 土木工程学报, 2010, 43(2): 39−47. LUI Jingbo, LIN Yangbing, YAN Qiushi, et al. Performance-based seismic fragility analysis of CFST frame structures[J]. China Civil Engineering Journal, 2010, 43(2): 39−47.

[2] HWANG H, 刘晶波. 地震作用下钢筋混凝土桥梁结构易损性分析[J]. 土木工程学报, 2004, 37(6): 47−51. HWANG H, LIN Jingbo. Seismic fragility analysis of reinforced concrete bridges[J]. China Civil Engineering Journal, 2004, 37(6): 47−51.

[3] 何益斌, 李艳, 沈蒲生. 基于性能的高层混合结构地震易损性分析[J]. 工程力学, 2013, 30(8): 142−147. HE Yibin, LI Yan, SHEN Pusheng. Performance-based seismic fragility analysis of tall hybrid structures[J]. Engineering Mechanics, 2013, 30(8): 142−147.

[4] CIMELLARO G P, ASCE A M, REINHORN A M, et al. Multidimensional performance limit state for hazard fragility functions[J]. Journal of Engineering Mechanism, 2011, 137(1): 47−60.

[5] 郑山锁, 杨威, 杨丰, 等. 基于多元增量动力分析方法的核心筒结构地震易损性分析[J]. 振动与冲击, 2015, 34(1): 117−123. ZHENG Shansuo, YANG Wei, YANG Feng, et al. Seismic fragility analysis for RC core walls structure based on MIDA method[J]. Journal of Vibration and Shock, 2015, 34(1): 117−123.

[6] 李刚, 程耿东. 基于性能的结构抗震设计: 理论、方法与应用[M]. 北京: 科学出版社, 2004: 1−150. LI Gang, CHENG Gengdong. Theory, method and application of performance-based seismic design[M]. Beijing: Science Press, 2004: 1−150.

[7] 赵明伟, 顾明. 轻型钢结构风灾易损性概率分析[J]. 中南大学学报(自然科学版), 2012, 43(9): 3609−3618. ZHAO Mingwei, GU Ming. Probabilistic wind vulnerability analysis of light-weight steel buildings[J]. Journal of Central South University (Science and Technology), 2012, 43(9): 3609−3618.

[8] FEMA 356, Prestandard and commentary for seismic rehabilitation of buildings[S].

[9] VAMVATSIKOS D, FRAGIADAKIS M. Incremental dynamic analysis for estimating seismic performance sensitivity and uncertainty[J]. Earthquake Engineering and Structural Dynamics, 2009, 39(2): 141−163.

[10] GB 50011—2010, 建筑结构抗震设计规范[S]. GB 50011—2010, Code for seismic design of buildings[S].

[11] 刘博文, 徐开, 刘畅, 等. perform-3D在抗震弹塑性分析与结构性能评估中的应用[M]. 北京: 中国建筑工业出版, 2014: 20−45. LIU Bowen, XU Kai, LIU Chang, et al. Seismic elastic-plastic analysis and performance-based evaluation with perform-3D[M]. Beijing:China Architecture and Building Press, 2014: 20−45.

[12] 门进杰, 史庆轩, 周琦. 平面不规则钢筋混凝土框架结构基于性能的抗震评估方法[J]. 土木工程学报, 2008, 41(9): 60−67. MEN Jinjie, SHI Qingxuan, ZHOU Qi. Method of performance based seismic evaluation for irregular plane reinforced concrete frame structures[J]. China Civil Engineering Journal, 2008, 41(9): 60−67.

[13] 钱稼茹, 姜鋆. 判别结构扭转不规则的位移比计算方法探讨[J]. 建筑结构, 2006, 36(12): 80−82. QIAN Jiaru, JIANG Jun. Study on calculating methods of displacement ratio used to judge structural torsion irregularity[J]. Building Structure, 2006, 36(12): 80−82.

[14] LAGAROS N D. Multi-component incremental dynamic analysis considering variable incident angle[J]. Structure and Infrastructure Engineering, 2010, 6: 1−2, 77−94.

[15] 吕大刚, 于晓辉, 潘峰, 等. 基于改进云图法的结构概率地震需求分析[J]. 世界地震工程, 2010, 26(1): 7−15. LÜ Dagang, YU Xiaohui, PAN Feng, et al. Probabilistic seismic demand analysis of structures based on an improved cloud method[J]. World Earthquake Engineering, 2010, 26(1): 7−15.

[16] 常泽民. 钢筋混凝土结构非线性抗震可靠度及地震易损性分析[D]. 哈尔滨: 哈尔滨工业大学土木工程学院, 2006: 5−25. CHANG Zemin. Nonlinear seismic reliability and fragility analysis of RC structures[D]. Harbin: Harbin Institute of Technology. School of Civil Engineering, 2006: 5−25.

(编辑 赵俊)

Performance-based seismic fragility analysis of plane irregular structure

HUANG Xiaoning1, DU Yongfeng1, 2, LI Hui1, 2

(1. Institute of Earthquake Protection and Disaster Mitigation, Lanzhou University of Technology, Lanzhou 730050, China;2. Western Center of Disaster Mitigation in Civil Engineering of Ministry of Education,Lanzhou University of Technology, Lanzhou 730050, China)

A performance-based method to calculate fragility functions of plane irregular RC frame-shear-wall structures was proposed. Using the method of performance-based static elastoplastic pushover analysis, according to definition of the ultimate damage states of the structure, four performance level limits of threshold values of inter-story drift angles and inter-story torsion angle were proposed. Structural seismic response was obtained through nonlinear dynamic time history analysis. Concerning conception of the probability of exceedance, the analytical solutions were proposed with performance level limits. Combined with the peak ground acceleration and the probability of exceedance, the performance-based seismic fragility analysis was carried out using this method, and fragility curves were derived to assess and compare the seismic performances of the structure. The results show that torsion response should be considered for analyzing irregular RC frame-shear-wall structures.

plane irregular frame-shear-wall; inter-story drift angle; inter-story torsion angle; performance level; seismic demand analysis; fragility curve

10.11817/j.issn.1672−7207.2017.06.031

TU352.1+1

A

1672−7207(2017)06−1645−06

2016−07−18；

2016−09−01

国家自然科学基金资助项目(51578274，51178211) Projects(51578274, 51178211) supported by the National Natural Science Foundation of China)

杜永峰，博士，教授，博士生导师，从事结构抗震性能评估研究；E-mail：dooyf@sohu.com