代数运算在逻辑推理中萌生*
2017-07-20安振平
●安振平
(咸阳师范学院教育科学学院,陕西 咸阳 712000)
代数运算在逻辑推理中萌生*
●安振平
(咸阳师范学院教育科学学院,陕西 咸阳 712000)
文章通过两道数学问题,探究了代数运算过程中逻辑思维萌生的缘由,为学习解决数学问题、展开数学思维的逻辑推理,进行了有益地实例思考.
变形化归;代数运算;逻辑推理;萌生
学习数学需要积累基础知识、总结解题方法、提炼数学思想.在模式识别、差异分析的过程中,进行不断地变更、变形、转化和化归,实现陌生问题熟悉化、抽象问题具体化、复杂问题简单化.运用逻辑推理的力量实施代数运算、几何直观,以及数与形二者的双向沟通.本文通过对具体问题的解题分析,谈谈笔者的一些思考,愿对读者有所启迪.
例1 过定点P(2,1)的直线l交x轴正半轴于点A,交y轴正半轴于点B,O为坐标原点,则△OAB周长的最小值为
( )
A.8 B.10 C.12 D.45
例1是某地区2010届高中毕业生调研考试的一道测试题.关于该问题的讨论在一些刊物上虽已多见,但寻找简单明了的适合高中生学习实际的解答方法,依然是一个值得探究的有趣话题.
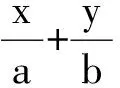



巧妙解答 设△OAB的周长为p,利用柯西不等式和二元均值不等式,得
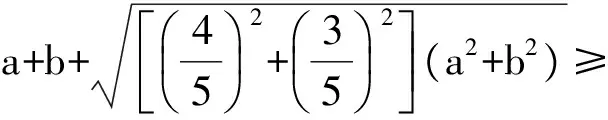

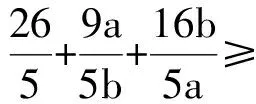


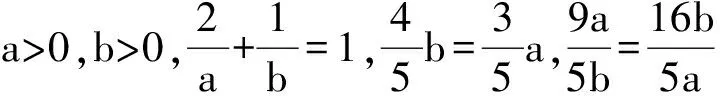

解得
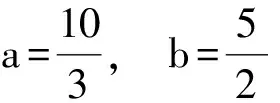
一般解答 引入待定正的参数m,n满足m2+n2=1.利用柯西不等式和二元均值不等式,得
(添加因式,创造用柯西不等式的环境)
a+b+ma+nb=(用柯西不等式“化掉”根式)
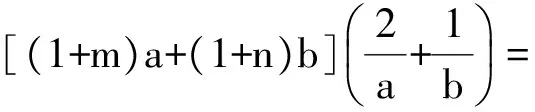

(用二元均值不等式).
等号成立的条件为
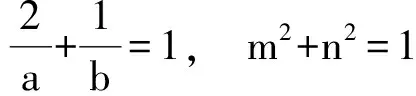

解得
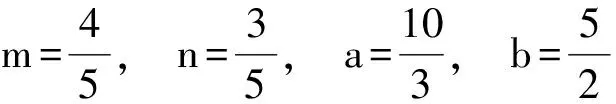

学习数学、体验数学、感悟数学的进程中,需要多问几个为什么?问题的条件是什么?解题目标是什么?为什么要这样去实施变形?不这样变形行吗?根据自己的已有知识经验,你还有其他解答方法吗?比如:对上文的变形问题,你能用条件“解代消元”后,转化为一元函数,运用求导方法解答吗?
待定系数法是数学解题的通性通法,你能感悟到其中的解题机智、解题智慧吗?我们不妨再举一例说明之.

本题为第二届(2011年)陈省身数学奥林匹克竞赛试题第6题,对左边不等式可以用配方法证之;对右边不等式,同样可以利用二元均值不等式,并结合待定系数法实现证明.
证明 先证左边不等式.因为
3(x2+y2+2z2)+2(3xy+yz+zx)=(作差变形)
3x2+3y2+6z2+6xy+2yz+2zx=(代数变形)
6z2+2(x+y)z+3(x+y)2=
(整理为主元z的二次三项式)


再证右边不等式.利用二元均值不等式,得




从而

因此 2(3xy+yz+zx)≤ (3+a2)(x2+y2+z2)=
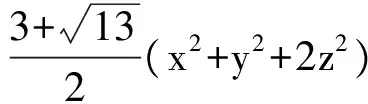
即
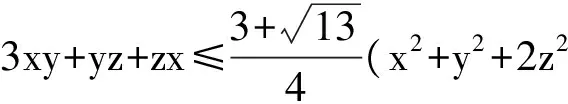

其实,应用均值不等式解题,其要害是平衡系数、分配因子,而待定系数法能化“未知”为“可知”,实现问题的化归.作为解题的通性通法,配方法和待定系数法是基本的、常用的,在学习过程中,应多加关注和重视.
从方法到能力、到思想,需要不断地、反复地思考、探究、琢磨和总结,且行且思,我思故我在,唯有深思、远思、勤思,方可通过有限道问题的演练获得解答无限道问题的思维智慧.
�2017-05-22;
2017-06-30
安振平(1961-),男,陕西永寿人,陕西省特级教师.研究方向:数学教育.
O122.3
A
1003-6407(2017)08-30-02
