关系暗含难定断 “隔离”明言易呈现*
2017-07-20郑良
●郑 良
(灵璧第一中学,安徽 灵璧 234200)
关系暗含难定断 “隔离”明言易呈现*
●郑 良
(灵璧第一中学,安徽 灵璧 234200)
高三专题复习教学中会出现很多解法上的困惑.文章研究剖析了一道试题的解法,明晰问题的逻辑基础,给出相关问题的解答与点评,并从问题背景、思维历程、逻辑关系等多角度进行揭示,同时针对教学现状,结合教学实践给出教学思考.
高三复习教学;“隔离”函数;凹(凸)函数;传递性;思维过程;自然解法
1 问题提出
在高三“函数与导数”的专题复习教学中,笔者曾给出如下问题:
例1 已知函数f(x)=x2lnx,且x1≠x2,满足f(x1)=f(x2).求证:x1+x2>1.
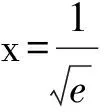
证明 由函数f(x)的单调性可得

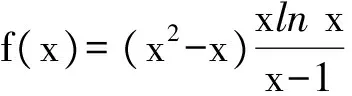
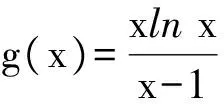
m(x1) 即 从而 (x2-x1)(x2+x1-1)>0. 因为x2-x1>0,所以 x2+x1>1. 学生惊奇于函数构造的巧妙,困惑于:为什么要如此隔离函数g(x)、怎么想到如此隔离、什么情况下需要用到“隔离”函数、如何确定隔离函数等. 通过比较,能对两种或两种以上同类的事物辨别异同或高下.如数学中比较数的大小,常有以下方法:作差法(将差与0比较)、作商法(将商(分母不为0)与1比较)、图像法(通过图像上点的高低来判断)、单调性法(正用或逆用构造的函数的单调性)、中间值法(通过中间值进行大小关系的传递).同样,判断两个函数(包含常数函数)的大小关系更值得我们关注.学生将以上解法与已存储的解法模型进行比对,发现无法对号入座,此时更能激发其探究的兴趣,从而化突兀为自然,深化对问题的理解. 一般地,当两个函数的大小关系不易确定(如函数的种类不同、差函数的导数符号难以确定等)时,往往根据两个函数的结构特征选择与两者相关的中间函数进行牵线搭桥,实现沟通.“间隔”函数的选择未必唯一,它需要由f(x)与g(x)的“亲密”程度决定:若f(x)与g(x)的关系松散(差距较大),则有无数个h(x)可趁虚而入,反之,则需要不断地调试才能确定函数h(x),特别地,当f(x)=g(x)时,f(x)与g(x)的“间隔”函数只能是其本身.选择的“隔离”函数要尽可能简单,如两个函数对应曲线的公切线所对应的函数等,更应通过知识的积累(如常见结论ex≥x+1)、方法的调整等方式分析和解决问题. 1)求实数a,b的值; 2)若x≥0,求证:f(x)≤g(x). (河北省石家庄市2017届高三复习教学质量检测一理科试题第21题) 2)证明 由第1)小题可知 即证 显然此式成立. 综上所述,当x≥0时, 即 f(x)≤g(x). 点评 对于第2)小题,若令φ(x)=g(x)-f(x)(其中x≥0),则 例2通过两条曲线的公切线实现了有效传递过渡,若两条曲线的公切线不易找到,则可考虑分别寻找其“隔离”函数进行传递. 例3 已知函数f(x)=2ex-x2-2x-2. 1)判断函数f(x)在R上的单调性; 1)f(x)在R上的单调递增(过程略). 2)证明 由第1)小题知,当x>0时, f(x)>f(0)=0, 从而 于是 点评 第2)小题中待证不等式左、右两边的函数类型不同,直接作差求证几乎不可能.尝试通过“某函数”进行隔离(传递)是否可行?以下从待证不等式两边所对应的两个函数的性质(背景)出发进行探究: φ′(x)=x2ex>0, 从而φ(x)在(0,+∞)上单调递增,于是 φ(x)>φ(0)=0, 即函数m(x)为(0,+∞)上的下凸函数,且 亦即“m(x)在x=0处的切线为y=x”,因此对任意x>0,恒有m(x)>x.因为函数n(x)是周期为2π的周期函数,且当x∈(π,2π)时,n(x)<0,所以先研究函数n(x)在[0,π]上的性质. 例3仍然通过函数m(x),n(x)在“x=0”处的公切线来过渡,不同的是m(x)在“x=0”处没有定义,通过洛必达法则巧妙实施. 1)若f(x)在[0,+∞)上单调递增,求实数m的取值范围. 2)当a≥1时,任意x∈[0,+∞),问:不等式sinx-cosx≤eax-2是否恒成立?请说明理由. 1)实数m的取值范围为(-∞,1](过程略). 2)证法1 由第1)小题知,当x∈[0,+∞)时,sinx≤x,且 即 从而 由M′(x)=ex-x-1知M(x)在[0,+∞)上单调递增,从而 M(x)≥M(0)=0, 证法2 记φ(x)=ex-2-sinx+cosx,x∈[0,+∞),则 φ′(x)=ex-cosx-sinx, φ"(x)=ex-cosx+sinx. φ"(x)≥1-1+sinx≥0; φ"(x)≥e1-1-1>0, 即对任意x∈[0,+∞),φ"(x)≥0,从而φ′(x)在[0,+∞)上单调递增,φ′(x)≥φ′(0)=0,即函数φ(x)在[0,+∞)上单调递增,于是 φ(x)≥φ(0)=0, 即 ex-2≥sinx-cosx. 因此,当a≥1时,对任意x∈[0,+∞),sinx-cosx≤ex-2≤eax-2恒成立. 点评 两个函数的“亲密”程度不同,选择的“间隔”函数必须满足精度要求.对于第2)小题,证法1利用二次多项式牵针引线(背景是y=sinx,y=cosx,y=ex的泰勒展开式);证法2通过对自变量的合理划分,直接构造函数求解,体现了解法的多样性.我们在解题时不能迷信于参考答案,而应强化多方联系,细化分析,优化策略. 4.1 教师要做有心人 随着社会节奏的加快,知识(不限于静态的知识内容)成指数爆炸式增长.教师必须做个有心人,及时更新理念,接纳新知识,提高技能与方法,在甄别中提炼,在比较中澄清,在优化中提升.只要我们有心、用心,资源才不会从身边溜走,课堂上才能避免“滑过”现象的发生.如我们对“隔离”函数并不陌生,分离参数法就是“隔离”函数的应用之一.隔离函数的逻辑基础是什么(不等式的传递性)、怎么想到“隔离”函数(直接求解碰壁后从充要条件角度辨识)、如何找到合适的“隔离”函数(知识的积累为背景的揭示提供粮草库,通过审题找到分析问题的起点、方向及可能的调整策略)等等,只有在解题时留意上心,才能使知识结构系统化、思维程序条理化、方法策略优质化. 4.2 教师要做明白人 以己昏昏,岂能使人昭昭.面对新事物(知识、方法)带来的诸多困惑,我们不能怨天尤人,更应主动出击,做个明白的教师,这是“传道、授业、解惑”的前提.教师要理解数学、理解教学、理解学生,才能做到因材施教.教学中,教师要想学生所想、惑学生所惑、重走学生思维之路,从而引领学生到达解决问题的彼岸. 4.3 教师要追求高尚 耽误时间无异于扼杀生命.少数教师业务不专,教学中让学生在题海中归纳、在操作中感悟,事倍功半,导致学生逐渐丧失对数学的兴趣甚至厌恶数学.众所周知集腋成裘的道理,一个教师一辈子接触上万个学生,若为每个学生节省10分钟,创造的价值与意义非常巨大.具有高尚情操的教师,教学时会瞄准高考而不囿于高考,如教师可根据学生的具体情况,适度补充洛必达法则、中学阶段常见函数的泰勒展开式等拓展性内容.跳出圈子看世界,让学生品味数学文化,提升数学素养.因此,我们要尽可能地深入研习,在获得更好的课堂教学效益的同时,创造出更多的社会价值. �2017-04-17; 2017-05-20 郑 良(1980-),男,安徽灵璧人,中学高级教师.研究方向:数学教育. O122.1 A 1003-6407(2017)08-23-04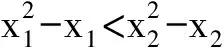
2 案例剖析
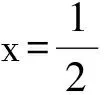
3 问题链接与简评
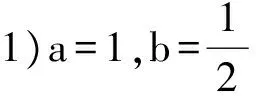

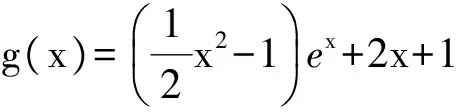
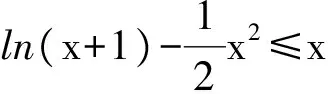
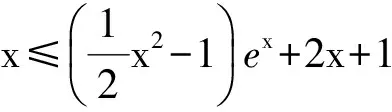
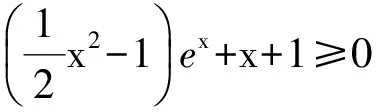
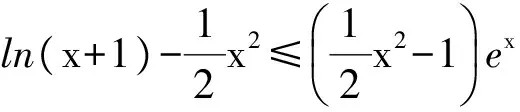
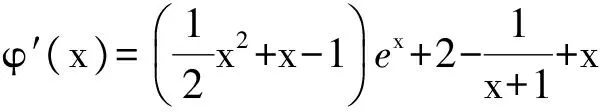
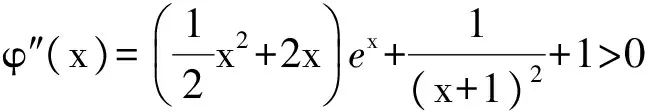


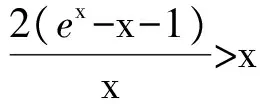

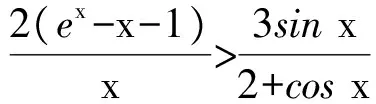



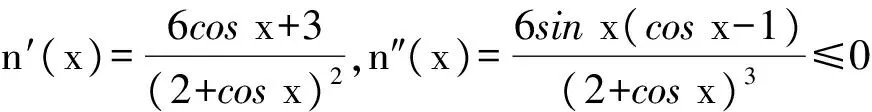


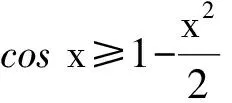


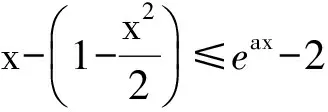
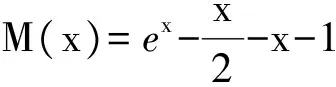

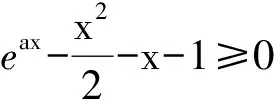

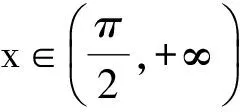
4 教学思考
