排列组合中“算错”的两大原因分析*
2017-07-20侯胜哲
●侯胜哲
(华南师范大学数学科学学院,广东 广州 510631)
排列组合中“算错”的两大原因分析*
●侯胜哲
(华南师范大学数学科学学院,广东 广州 510631)
文章对高中学生在排列组合问题中出现的常见错误进行分析整理,挖掘出错的深层原因,帮助学生真正理解解决排列组合问题的思考方式.同时针对常见的两种错误分别给出纠正办法,介绍了容斥原理和分类讨论的思想,帮助学生解决在排列组合问题中总是算错的疑惑.
排列组合;容斥原理;分类讨论;多加漏减
在解决排列组合问题上,学生常常会遇到这样的情况,认为自己的分析很有道理,但是一对照参考答案发现并不一样,却找不出到底哪里出了问题,这该怎么办呢?笔者针对这样的问题进行探讨,找出逻辑上容易疏漏的因素分析了两大原因,供读者解惑.
1 两条件可以叠加,用容斥原理改善
例1 有数1,2,3,4,5,6,7,求作成1与2相邻或3与4相邻的全排列个数.
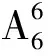
可是一对照参考答案后发现答案是2 400,上面的分析错在哪儿?教师上课的例题“有数1,2,3,4,5,6,7,求作成1与2相邻的全排列个数”不就是用捆绑法做的吗?难道出什么问题了吗?思来想去发现,多加了一个条件就行不通了,加了“或3与4也相邻”,似乎就有一部分多算了,多算了什么呢?请大家先自己思考一下.下面先介绍“容斥原理”,学了这个原理后,学生对这样的题目就会有更深的认识.

容斥原理可以有多种方法来讲解,但笔者认为容斥原理的核心就是“画图”,于是笔者通过图像来讲解.

图1
如图1,如果被计数的事物有3类,用集合A,B,C来表示,那么各个集合的元素个数就是各个类可能出现情况的种数,用加绝对值来表示,如|A|表示A类可能出现的情况种数.再结合图形语言(韦恩图),用面积表示集合的个数.
要求A,B,C这3类都发生可能出现的情况种数|A∪B∪C|,即将A,B,C这3个集合的元素个数相加,但发现两两重叠的部分重复计算了1次,于是减去A∩B,A∩C和B∩C,但这样一来,3个集合公共部分又被重复计算了1次,于是加上|A∪B∪C|,即|A∪B∪C|= |A|+|B|+|C|-|A∩B|-|A∩C|-
|B∩C|+|A∩B∩C|.
这样叙述未免抽象,下面用一道例题来说明.
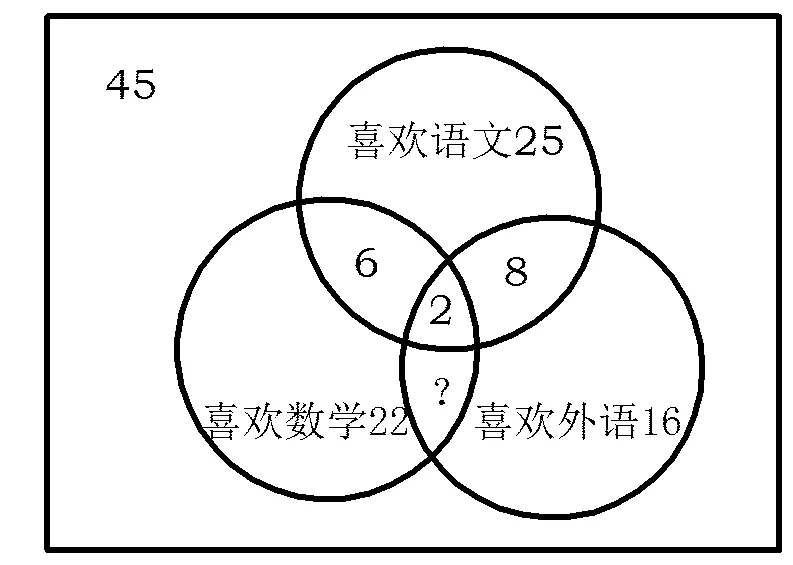
图2
例2 一个班有45个同学,喜欢语文的有25人,喜欢数学的有22人,喜欢外语的有16人,其中既喜欢语文又喜欢数学的人数为6人,既喜欢数学又喜欢外语的有8人,有3个同学一科也不喜欢,2个人喜欢所有科目,问既喜欢语文又喜欢外语的有几人?
解 先画图(如图2所示),由于|A∪B∪C|= |A|+|B|+|C|-|A∩B|-|A∩C|-
|B∩C|+|A∩B∩C|,即喜欢语文或数学或外语的人数=喜欢语文的人数+喜欢数学的人数+喜欢外语的人数-既喜欢语文又喜欢数学的人数-既喜欢语文又喜欢外语的人数-既喜欢数学又喜欢外语的人数+既喜欢语文又喜欢数学又喜欢外语的人数.
因此,既喜欢数学又喜欢外语的人数有9人.
通过例2可以发现,会出现即喜欢数学又喜欢语文的情况,也就是说,喜欢数学和喜欢语文这两种类别是可叠加的,这时往往会想到容斥原理.容斥原理是解决可叠加分类的利器,其基本原理是:先不考虑重叠的情况,把包含于某内容中的所有对象的数目先计算出来,然后再把计数时叠加计算的数目排斥出去,使得计算的结果既无遗漏又无叠加,简单来说先“容”再“斥”.当然在解题中我们往往用图像来表示,并不直接用到其基本原理.
了解了容斥原理,再回到例1,1与2相邻和3与4相邻这两个分类是可叠加的吗?也就是说会有“在一次排列中,出现1与2相邻且3与4相邻”的情况吗?显然会出现.因此在例1中,1与2相邻和3与4相邻这两个分类可叠加,1与2相邻且3与4相邻可能算了多遍或少算了,故可以借助容斥原理来梳理.
2 两条件不独立,用分类讨论来改善
还有一种情况,是之前的结果对之后可能发生的情况产生影响,解题时往往没有考虑到这种影响而使题目解错.
例3 求万位数字不是5,个位数字不是2,且各位数字相异的5位数的个数.

图3
分析 如图3,万位不是5,则可能是1,2,3,4,6,7,8,9这8个数;个位不是2,且由于各位相异,因此也不能是万位数取过的数,加上0,则有8种情况;千位数不能是个位数和万位数,则有8种情况;百位数有7种情况,十位数有6种情况,故有8×8×7×6×8=21 504种情况.
但是参考答案给的是21 840种情况,问题出在哪里呢?仔细一想发现:假如万位是2,这时个位就不是8种情况了.此时,个位可以填0,1,3,4,5,…,9,这说明万位发生的结果(万位数字不是5)可以影响到个位发生的结果(个位数字不是2).
因此,“万位数字不是5”和“个位数字不是2”这两个条件不独立.如何判断两个条件是否独立呢?其中一个条件“已经”发生了,观察它是否对另一条件产生影响(而不是像判断可叠加时,强调两个条件是否有重叠的部分,是否多加了或少加了,这是时空上的差别).
那么怎么办呢?可以用“分类讨论”把各个情况分开来,以达到去多的目的.
1)若2在万位,则万位有1种情况,个位有9种情况,千位有8种情况,百位有7种情况,十位有6种情况,共1×8×7×6×9种情况.
2)若2不在万位,则万位有7种情况,个位有8种情况,千位有8种情况,百位有7种情况,十位有6种情况,共7×8×7×6×8种情况.
综上所述,满足题意的5位数共有1×8×7×6×9+7×8×7×6×8=21 840种情况.
不少学生常犯上面的错误,而涂色问题也属于这种类型的问题,常见的有点着色问题和面着色问题.下面具体通过一道高考题,看看到底怎么易错.
例4[2]某城市在中心广场建造一个花圃,花圃分为4个部分(如图4),现要栽种7种不同颜色的花,每部分栽种一种且相邻部分不能栽种同样颜色的花,则不同的栽种方法有________种(以数字作答).

图4 图5
分析 有学生这样解答(按照1,2,3,4的顺序着色):共有7×6×6×5=1 260种情况,而参考答案是1 302.到底错在哪呢?
仔细思考:如果1号、3号苗圃同色,那么4号花圃还是可能涂5种颜色吗?显然变了,4号花圃可能涂6种颜色.这就是之前涂的颜色对后面的涂色产生了影响,本质原因是他们之间不独立,而是相关联的.此时要分类讨论,把各种情况区分开来.
1)若1号、3号苗圃不同色(如图6所示),则共有7×6×5×5=1 050种情况.
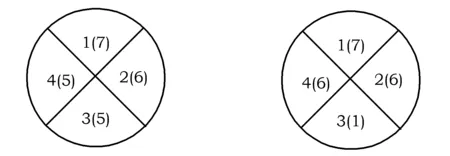
图6 图7
2)若1号、3号苗圃同色(如图7所示),则共有7×6×1×6=252种情况.
综上所述,共有1 050+252=1 302种情况.
部分教师讲解时也存在上述问题,不能给学生解释哪儿出错了,而是直接给出正确的方法.一些学生说“知道了”就过去了.实际上部分学生因为害羞而不敢追问,这就导致下次遇到相关的试题还是无法做对.了解容斥原理和分类讨论的思想,能让我们知道排列组合常出错的逻辑原因,直面错题,深入思考错题,让我们在数学的解题中获益匪浅.
[1] 曹汝成.组合数学[M].2版.广州:华南理工大学出版社,2012.
[2] 朱孝春.解排列组合问题十法[J].数理化学习:高中版,2010(5):22-24.
�2017-04-17;
2017-05-26
侯胜哲(1994-),男,华南师范大学本科学生.研究方向:数学教育.
O122.4
A
1003-6407(2017)08-14-03
