让理性的数学课堂开出感性之花*
——浅谈数学文化在函数概念教学中的应用
2017-07-20萧山区第二高级中学浙江杭州311251
●周 燕 (萧山区第二高级中学,浙江 杭州 311251)
●朱 哲 (浙江师范大学教师教育学院,浙江 金华 321004)
让理性的数学课堂开出感性之花*
——浅谈数学文化在函数概念教学中的应用
●周 燕 (萧山区第二高级中学,浙江 杭州 311251)
●朱 哲 (浙江师范大学教师教育学院,浙江 金华 321004)
高中数学课程改革的一个亮点在于强调了数学史和数学文化的重要性.在课堂上科学合理地渗透数学文化,能帮助教师更好地突破教学难点,激发学生学习兴趣.以函数概念的教学为例,教师可以从实例的引入和符号的解释入手,将数学文化融入课堂、辅助教学;同时可以借助函数概念的演变过程,将数学史穿插于教学之中,帮助学生走出函数概念的认知误区.
数学史;数学文化;函数概念;数学教学
数学教学在大部分教师眼里,等同于解题技巧的传授、运算能力的培养和逻辑思维的训练.数学学习中过度的形式化和抽象性,使学生感到枯燥乏味.但其实数学也具有社会性,也和文化相通.历史上的许多文化名人,往往本身就是数学家,如达芬奇和柏拉图.事实上,对现代教师而言,数学教育不光要进行知识的传播,还要注重文化的熏陶,使学生在学习过程中感受到数学科学价值和人文价值的统一.
德国数学家克莱因曾把函数比作数学的灵魂[1],它在高中数学课程中占有重要的地位.但是函数的概念因其表述抽象、符号繁多,往往使学生望而生畏,从而难以入门.其实,函数的发展过程蕴含着丰富的实际背景和文化内涵,笔者认为:若能将其服务于课堂,则必能使教学达到事半功倍的效果.
以下是笔者关于如何将数学文化融入函数概念课的一些做法和构想,以期在完成教学任务的同时获得更好的教学效果.
1 从丰富的实际背景中引入函数的概念
《普通高中数学课程标准实验教科书(必修)·数学1(A版)》分别从炮弹高度、臭氧层空洞面积和恩格尔系数这3个实例引入,建构概念.这不仅能让学生们体会到函数在实际生活中的广泛应用,也能帮助他们突破对函数对应关系认识的局限性.教材上的实例虽具有科学性和典型性,但笔者认为它们缺少时效性和趣味性.这里,笔者以发射天宫二号运载火箭为背景,提供引入函数和建构概念的4个例子.
例1 2016年中秋节9月15日22时04分,搭载天宫二号空间实验室的长征二号运载火箭在中国酒泉卫星发射中心点火发射.下面,请同学们就发射过程探讨以下4个问题.
1)火箭在进入正常轨道后,运动轨迹可近似地看成和地球共圆心的圆,那么请问此时天宫二号距离地面的高度h与时间t之间的关系是否为函数关系?
2)火箭发射时大致可看成是匀加速直线运动,那么它的速度v与发射时间t之间的关系(可以解出表达式)是否为函数关系?
3)发射过程中,火箭外的大气压P随高度h的变化而变化(可给出大致曲线),请问P是否为关于h的函数?
4)发射天数t和燃料剩余情况y之间的关系(给出表格)是否为函数关系?
在一个大前提下完成概念的引入和建构的过程,可以使课堂显得更加连续和完整,同时也能节约学生上课阅读题干的时间,提高课堂的效率.另外,后面3个问题的研究正好涵盖了用解析式、图像和表格来反映对应关系的3种情况,可谓和教材的例题异曲同工,但却更加新颖有趣、与时俱进.
2 从形象的比喻中理解符号的作用
《普通高中数学课程标准实验教科书教师教学用书(必修)·数学1(A版)》中指出:本节课的教学难点在于函数概念及符号的理解.但教材中没有提及为何要引入符号f.许多教师在解释y=f(x)时也只是强调“f(x)是一个函数符号,表示y是x的函数”,这样的效果往往不能让人满意.函数概念的历史源远流长,各种符号的出现也有其根源,若在课堂上穿插“f”的故事,生动形象地解释“y=f(x)”的含义,不失时机地向学生渗透数学文化的价值,不仅能使他们更好地理解抽象的概念,更能培养他们对数学学习的兴趣.
国外的教材称函数为function,它是德国哲学家莱布尼茨于1673年最早引进的,因此书上常用f来表示函数中的对应法则.在我国,清代数学家李善兰首次把英文“function”翻译成“函数”.“函”即“匣”,盒子的意思.因此符号f可以看成是一个盒子,它的作用就是把放x进去之后经过一系列变换变成唯一确定的y值[2].例如f(x)=2x+3,就是把x放进这个f的盒子后,它先乘以了2再加上了3得到一个新的数y.这个盒子就可以理解为函数概念的对应法则.在提出把f看成盒子之后,教师可以用“函数机器”的比喻来形容函数的对应关系[2]:即将f看成一个机器,例如解释f(x)=2x+3时,可以给出如下图1:

图1
用生动的比喻和直观的图形解释f的作用,可使对应关系形象化.另外函数机器的用法在后续学习求抽象函数定义域和求复合函数解析式时也有用武之地.
例2 已知f(x)=x4,g(x)=2x+3,求f(g(x))的解析式.
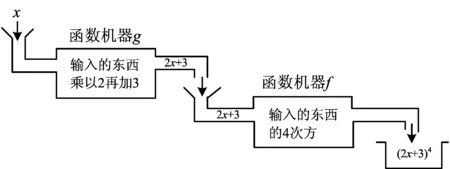
图2
如图2所示,课堂上可向学生解释复合函数实际上是x经过了两台机器的先后作用:先由内机器g将x变成2x+3,再将2x+3作为整体经过外机器f的加工,变成(2x+3)4.
例3 已知f(x+1)的定义域为[1,2],求函数f(3-x)的定义域.
抽象函数的定义域问题一直来都困扰着学生,教师在讲解这部分内容时可以借助上述比喻,帮助学生更好地理解其做法.如图3所示,即对于同一台函数机器f而言,放进去的“产品”,即括号中的整体,其规格和型号都必须相同.

图3
引入函数机器的比喻,将对应关系形象化、具体化,不仅可以有效减少概念的抽象性给学生的理解带来的困难,而且能帮助学生更好地吃透函数概念中所蕴含的本质和精髓.
3 从函数的发展史中深化函数本质的理解
在教学中,教师往往会通过练习的形式或注意事项的提醒,来清除学生认知上的盲区.那么能否换个方式,让学生在课堂上循着数学家们的脚步去寻找概念产生的历史踪迹;让他们看一看困扰着他们的问题在历史上是否也一样困扰过科学家们;让他们感受一下先人们是如何通过解决这些问题来推动函数概念的发展的.在具体教学中,教师可以按照以下流程,分4个阶段介绍函数的发展史.
1)函数的萌芽.
法国数学家笛卡尔在《几何学》中提出了变量的思想,同时引入两个变量之间关系的数学概念.而科学家们在探索发现世界的过程中,特别是研究物体运动的过程中,不断遇到各种需要能准确表示两个变量之间关系的数学概念.
课堂上通过介绍函数的萌芽,让学生感受到函数概念的产生并非是凭空的,而是社会和科学发展的结果.而数学知识的来源往往是朴素的,依赖于人们的直观,这种质朴的数学思想,正是一种文化现象[3].
2)函数是解析式.
1748年,欧拉在出版的《无穷分析引论》中明确指出:函数是由一个变量与一些常量以任何方式形成的解析表达式[4].他认为一个函数就是一个解析式,一个函数对应一条连续的曲线[5].
事实上,学生在初中时期所学的一次函数、二次函数、反比例函数,都是典型的具有一个解析表达式的函数,都是那个时代的产物.让学生了解自己对函数认识的局限性,才能让他们拥有重新学习函数概念的动力.
3)函数是对应.
18世纪后半叶,欧拉和拉格朗日允许函数在不同区域上有不同的表达式,这与18世纪数学家们对函数的认识和理解相冲突,比如函数

和

就不满足“一个函数就是一个解析式”的观点.但是随着概念的扩充,这类函数也渐渐被纳入了函数的大家庭之中.随后,狄利克雷提出著名的函数

“一个函数对应一条连续的曲线”的观点也不攻自破了.1837年狄利克雷给函数下了一个定义:如果对于给定区间上的每一个x值都有唯一的y值同它对应,那么y就是x的一个函数,至于在整个区间上y是否按照一种规律依赖于x,或者y依赖于x是否可以用数学运算来表达,那都是无关紧要的[6].
在课堂练习“利用定义判断函数”时,就可以引入上述两个经典的函数.同时,教师可以通过讲解这一阶段历史,让学生走出“函数即是解析式”和“函数即是图像”的误区,深刻体会初、高中阶段函数概念的区别.
4)函数是关系.
上述函数的概念虽然摆脱了解析式和图像的制约,但是其中“依赖”“对应”等术语依然没有明确的界定和解释.而数学严格化的进程,要求函数的概念建立在已经定义的概念的基础之上[6].另一方面,19世纪末德国著名数学家康托的集合论的诞生以及映射概念的引入,为最终函数概念的完善奠定了坚实的基础.
而这个定义就是今天教材上所给出的,它使得函数概念得到了空前严格的程度.函数概念的演变过程,是由人们对运动与变化的研究、对客观世界的认识而推动的,经历了不断的争论和完善,是许许多多数学家们智慧的结晶.
在实际教学中,有一部分教师认为在课堂上渗透数学文化,穿插数学史,会挤压学生练习的时间,从而影响教学成绩,这其实是片面的.在函数概念的课堂上,若能让学生看一看它的内涵不断被精炼、深化、丰富的过程,是一件十分有意义的事情,它既培养了学生的理性思维能力,又使学生接受了人文精神的熏陶.
4 结语
以上是笔者对于数学文化融入函数概念教学的一点想法和做法,具体在教学中操作的流程如图4所示:
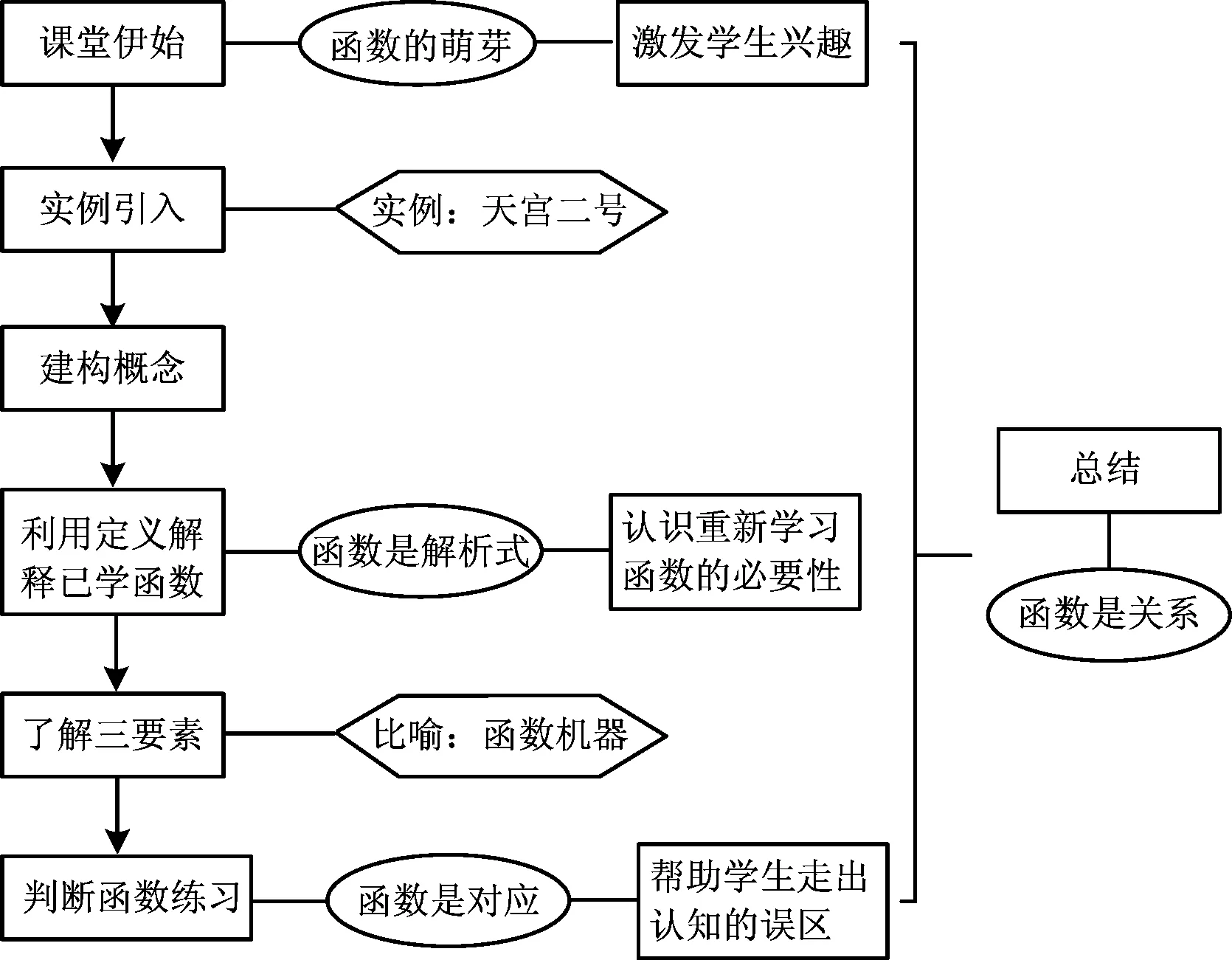
图4
课堂上数学文化的渗透是为了让学生在学习过程中形成“乐学”的态度.当数学文化真正丰富了课堂,融入了教学,学生心目中高冷的数学才会更“接地气”,数学就会通过文化的层面进一步被学生所理解和热爱.当然,这对我们众多教育者而言,任重而道远.
[1] 梁宗臣,王青建,孙宏安.世界数学通史[M].沈阳:辽宁教育出版社,1999.
[2] 倪露苹.函数概念难点研究及教学设计研究[D].上海:华东师范大学,2015.
[3] 黄孝长.高中数学新教材中的数学文化[D].金华:浙江师范大学,2008.
[4] 克莱因.古今数学思想(第二册)[M].上海:上海科学技术出版社,1979.
[5]StruikDE.ASourceBookinMathematics1200-1800[M].Cambridge,Massachusetts:HarvardUniversityPress,1969.
[6] 贾随军.函数概念的演变及其对高中函数教学的启示[J].课程·教材·教法,2008,28(7):49-52.
�2017-04-18;
2017-05-21
周 燕(1987-),女,浙江宁波人,中学一级教师.研究方向:数学教育.
O122.1
A
1003-6407(2017)08-07-03
