基于耦合分析与加权满意度的机械系统多目标协同优化方法

马 军 武柳洋 何文斌 明五一 曹 阳

郑州轻工业学院机电工程学院，郑州，450002



基于耦合分析与加权满意度的机械系统多目标协同优化方法

马 军 武柳洋 何文斌 明五一 曹 阳

郑州轻工业学院机电工程学院，郑州，450002

针对机械系统优化中因设计变量耦合关联导致的优化结果可靠性问题，提出了基于加权满意度的耦合关联机械系统多目标协同优化方法。建立机械系统设计变量耦合关联模型，采用最大-最小满意度函数法，并考虑各子目标的相对权重，建立基于权重加权和的多目标协同优化评价函数，将多目标优化问题转变为单目标优化问题。以掩护式液压支架四连杆机构-结构多目标协同优化为对象的应用表明，提出的方法简化了耦合关联机械系统多目标优化求解的复杂度，而且提高了优化结果的可靠性。

多目标优化；耦合关联；满意度；掩护式液压支架

0 引言

许多机械装备的主要承载构件是离散结构，如液压支架、升降台支架和夹持机器手等，这些离散结构必须通过一定的机构运动完成其承载功能，因此其本质上是一个机构-结构耦合关联的机械系统。在此类机械系统中，每个子系统(如机构和结构)都有其特定的功能和独特的设计方法，这些子系统相互协调，协同实现机械系统的整体功能。

近年来，许多学者对机构-结构耦合关联机械系统设计进行了研究，其研究思路一般是首先对结构进行设计，然后根据系统的性能要求设计机构系统。杨毅等[1]分别以结构柔度最小化和结构效率最大化为优化目标函数，对圆柱式折叠结构进行了拓扑布局优化。刘成颖等[2]针对机床结构薄弱件立柱进行结构优化，提出了一种基于拓扑优化、筋板形式选择与布局以及尺寸优化的结构设计方法。周明刚等[3]为提高船式拖拉机的动态性能，针对船式拖拉机机架进行多目标优化设计。罗文豹等[4]以平台可控性能和平台结构尺寸的加权综合最优为目标函数，采用加速遗传算法，对一款带防扭臂的三自由度平台的机构参数进行了优化。曹红娟[5]利用ANSYS 有限元软件对运载火箭上的面级发动机用机架的结构进行了优化。李晓舟等[6]运用数值分析软件MATLAB实现了异形片刹车机构的多目标规划和优化设计。李治多等[7]以各工况载荷下的结构刚度最大化为优化目标函数，基于线性加权和法建立多工况下结构拓扑优化设计模型。

已有文献研究表明，机构-结构耦合关联机械系统设计问题在大多数情况下是多目标协同优化问题[8]，也就是在整体系统优化目标中同时包含技术性(如机构的安全性和可靠性)和经济性(如结构的成本和质量)两类评价指标，而且各评价指标之间通常是互相冲突的，一般情况下不存在同时使所有目标都达到最优的解，而只能得到满意解[9]。但由于机械系统各个子目标的设计变量之间存在耦合关联性，得到的满意度函数的估计很不可靠，这使得常规优化方法在耦合关联机械系统多目标协同优化上受到很大限制[10]，设计决策者难以合理协调不同目标之间的冲突和耦合关系。

本文旨在解决机构-结构耦合关联机械系统设计中多目标、多变量耦合问题，提出机械系统耦合建模及其多目标协同优化方法，采用加权满意度函数法逼近多目标协同优化模型，从而获得相对优化的满意解，提高求解结果的可靠性。

1 耦合关联机械系统多目标协同优化方法

在耦合关联机械系统多目标协同优化中，各子目标的相对重要程度、数量级和量纲存在较大的差异，很难使其各子目标同时达到最优，而只能在设计决策过程中采用多目标协同处理方式，将复杂的多目标优化问题转变为较为独立的单一目标优化问题，并协调单一目标间的关联关系，以获得一个总体设计方案的满意解，显然这是一个反馈迭代、多方博弈的过程，其过程(图1)如下：

图1 机械系统多目标协同优化的处理过程Fig.1 The process of multi-objective cooperative optimization of mechanical system

(1)通过设计变量关联性分析，按耦合度定性区分设计变量的特征。

(2)建立设计变量的设计结构矩阵，对耦合变量进行解耦，以获得独立的优化变量。

(3)建立评价指标下各个子目标函数及其约束，并选择对应子目标的满意度函数形式。

(4)根据专家评价打分法，确定各子目标的相对重要性权重因子。

(5)对各子目标满意度函数加权，形成加权满意度的多目标评价函数。

(6)对加权满意度评价函数进行优化求解，并对解的满意解进行综合评价。

2 机械系统多目标协同优化中的耦合关联分析

机械系统多目标协同优化问题的典型特征就是各子目标通过设计变量发生关联，即一个目标领域内某些约束中的设计变量需要满足其他目标领域中的约束关系，甚至这些变量的决策权都是由其他目标领域控制的，因此，需要对设计变量进行全局分析。图2给出了一个典型的多目标协同优化耦合关联模型，描述了子目标间的耦合关系。

图2 机械系统多目标协同优化的耦合关联模型Fig.2 Coupled correlation model for multi-objective cooperative optimization of mechanical system

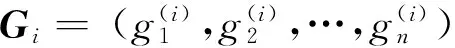
根据设计变量在耦合关联机械系统中发挥的作用，将其划分为系统变量、局部变量和接口变量三种类型。

(3)接口变量Yij(Yji)表示影响子目标j(i)但受目标领域i(j) 控制的接口变量。

显然，局部变量为子目标的独立优化变量而不需要解耦；系统变量在进行协同寻优过程中某一时刻，该变量的值在各子目标中是一致的，因此，尽管系统变量与接口变量可能会存在耦合关系，但可假设系统变量为常量，因此最终只有接口变量具有跨子目标的耦合关联现象，在进行协同寻优计算之前，必须经过解耦处理，使之在耦合关联机械系统各目标领域中发挥独立优化变量的作用。

设计结构矩阵是识别并解耦对象关联关系的有效方法，它以矩阵形式间接地表达了复杂过程中变量间信息的依赖关系[11]，如图3所示，该矩阵具有如下特性:

YnnX1X2…XnX1X2

⋮

图3 基于设计结构矩阵的设计变量解耦

Fig.3 Decoupling of design variables based on design structure matrix

(1)对称性。矩阵中以主对角线为对称轴的两元素相等。

(2)主对角线元素为1，表示变量与自身的耦合度。

(3)耦合矩阵表示机械系统中变量之间的耦合关系。

通过耦合矩阵，可以明确接口变量的数量和耦合度并进行处理，其基本思路是，在考虑子系统之间变量的输入输出关系时，接口变量可以通过其输入子目标系统内的表达式转换为局部变量，从而实现变量解耦。

3 基于加权满意度的耦合关联机械系统多目标协同优化模型

3.1 最大-最小满意度函数

满意度函数法是将每个子目标函数转换成满意度函数，求各子目标的几何均值，然后使其最大化，从而使多目标问题转化为单一目标问题。一般来讲，如果单一目标间具有一定的相关性，则基于满意度函数的优化将不可靠，但可通过最大-最小化指数满意度函数来对多目标函数进行建模，以获得稳健可靠的优化结果。

(1)对于最小期望，其满意度函数可表示为

(2)对于最大期望，其满意度函数可表示为

式中，ai为第i个子目标满意度函数si的当前解；dmin为第i个子目标满意度函数si的最小值；dmax为第i个子目标满意度函数si的最大值；mi为指数常数，决定满意度函数的类型，本文子目标满意度函数采用线性函数形式，即取mi=1。

3.2 多目标协同优化加权评价函数

评价函数构建有理想点法、最大最小法以及线性加权和法。其中，线性加权求和法选取不同的权重因子，进而获得多个加权满意度函数，通过求解多组最优解并进行比较，是一种最为简单有效的求解方法。

本文选取加权满意度作为多目标协同评价函数进行建模，即通过定义各子目标的权重因子，将多目标问题的评价函数线性化为各子目标满意度函数的加权。其中，权重因子的合理性直接影响最终优化结果的可靠性，这需要有一个客观的评价指标体系。

假定产品优化过程中需满足n个子目标，记为s=(s1,s2,…,sn)，它们对总体目标的权重记为W=(w1,w2,…,wn)。取2个子目标sk与sl，用wkl表示sk与sl对总体目标的影响之比，即各子目标两两相对重要程度的比较。全部比较结果用矩阵W=[wkl]表示，其中，wkl可用客观赋权法给定子目标的权值，如表1所示。

表1 评价指标量化指数

4 应用案例

掩护式液压支架是实现高效率、高产能的煤矿综采设备，该设备能够对综采工作面的顶板实现可靠的支撑和控制，对采空区进行隔离，并对回采工作面和推进输送机进行保护，防止矸石进入[12]。四连杆机构是掩护式液压支架的主要稳定和承力构件，为保证液压支架的强度和刚度及工作需求，四连杆的质量往往都很大，约占液压支架总质量的15%～20%[13]。对掩护式液压支架四连杆进行优化设计，目的在于寻求既安全又经济的掩护式液压支架系统，使其在提供最大承载前提下，减小结构质量，属于典型的机构-结构耦合关联的机械系统多目标协同优化问题。

4.1 掩护式液压支架四连杆机构-结构解耦分析

掩护式液压支架四连杆的拓扑结构如图4所示，其中，l1为后连杆长度，l2为掩护梁长度，l3为前后连杆上铰点距离，l4为前连杆长度，l5为前连杆下铰点与底座距离，l6为前后连杆铰点在底座的水平距离，α、γ、β分别为后连杆、掩护梁和前连杆的水平角度。

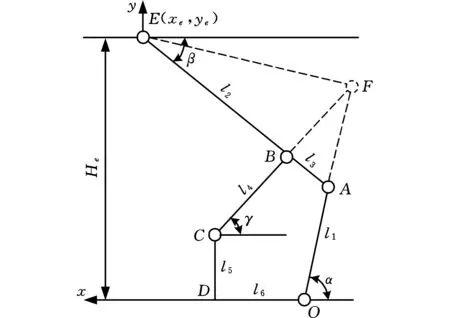
图4 掩护式液压支架四连杆的拓扑结构Fig.4 Topological structure of four-link of protective hydraulic support

由图4可知，顶梁运动轨迹与E点运动轨迹一致，只要已知任意高度He，则其他各铰点的位置都可计算出来。

然后根据掩护式液压支架实际工况，进行图5所示的液压支架四连杆机构动力学分析。

图5 掩护式液压支架四连杆的机构动力学分析Fig.5 Mechanism dynamic analysis of four-link of protective hydraulic support

联立如下方程组，可计算出支架顶梁所受外载荷以及前后连杆受力：

式中，Q为支架顶梁外载荷，方向与顶梁正交；μQ为纵向水平载荷；μ为顶板与顶梁间的摩擦因数；Nf、Nv分别为前后连杆受力；Ps为平衡千斤顶的推(拉)力；Pt为立柱支撑力；Kx、Ky分别为掩护梁重力K在x、y方向上的分力；Nxe、Nye分别为x、y方向上力的平衡方程；α1、α2分别为支柱工作阻力和平衡千斤顶推力与y方向的夹角。

4.2 优化模型的建立

基于上述掩护式液压支架四连杆机构-结构分析，根据优化变量独立性原则，掩护式液压支架四连杆机构-结构的关联解耦模型如图6所示。

图6 掩护式液压支架四连杆机构-结构耦合分析Fig.6 Mechanism-structure coupling analysis of four-bar of protective hydraulic support

根据掩护式液压支架四连杆机构-结构的关联解耦模型，取四连杆优化设计变量为

X=(x1,x2,…,x6)=(l1,l2,…,l6)

掩护式液压支架四连杆的优化目标就是求解具有最小质量的拓扑结构和最高的机构工作性能(包括结构变形、应力水平、整体与局部稳定性、动力特性)，使液压支架获得最优良的力学特性和最经济的制造成本，因此各子目标函数如下:

(1)在材料密度均匀的前提下，四连杆结构的总质量最小，即

式中，ρ为单位长度杆的质量，由于假定各杆材料密度相同，故ρ为一常量。

(2)为使结构发挥最大的承载能力，以各对应工况载荷下的结构刚度最大(即柔度最小)为子目标函数，即前后连杆的受力之和最小：

f2(x)=|Nf|+|Nv|

约束条件包括：①前后连杆的比值范围g1，即l4/l1为0.9～1.2；②前连杆的高度取值范围g2，即l4

4.3 优化模型的满意度函数

分别求出两个子目标函数在约束下的最优解和最劣解，如表2 与表3所示。

表2 子目标f1(x)的最优解与最劣解

表3 子目标f2(x)的最优解与最劣解

根据子目标函数的分布特征，建立基于各评价指标的子目标满意度函数，即

采用加权满意度对掩护式液压支架四连杆进行多目标协同优化，多目标评价函数为

minS(x)=w1s1(x)+w2s2(x)

由于掩护式液压支架四连杆的工作空间受限，优化目标重点应放在机构承载能力优化上，因此提升机构的承载能力明显比减小机构的体积重要。设结构质量评价指标的权重为w1，机构承载能力评价指标的权重为w2，根据表1取w1=1，w2=5，则权重判断矩阵为

S(x)=0.167s1(x)+0.8333s2(x)

优化结果如表4所示，评价函数S=0.956≥0.9，各目标函数的满意度s1=0.902≥0.9，s2=0.967≥0.9，符合满意度函数约束。

表4 优化前后设计变量对比

与优化前对比，优化后杆总长度减小2.8%(等同于杆总质量减小量)，前后连杆受力减小了5.4%。杆总长度减小量相对受力减小量小的原因，一是两目标函数进行了差异化的权重配置，二是设计变量对各目标函数的敏感性有差异。

5 结论

耦合关联机械系统多目标优化中各子目标往往是相互矛盾的，一般情况下不存在最优解而只能得到满意解，但由于设计变量的耦合性带来子目标的相关性，使得满意度函数估计很不可靠。本文通过机械系统多目标耦合关联解耦，将变量耦合关系转化为优化设计变量的一致性表达，在此基础上建立基于加权满意度的多目标协同优化评价函数，不仅提高了优化解的可靠性，而且还能对优化解进行满意度评价，从而更好地反映设计人员的设计意图和用户需求。虽然本文研究问题的引入对象是机构-结构耦合关联的机械系统，但该方法对其他具有复杂耦合关联现象的机械系统设计同样具有借鉴作用。

[1] 杨毅，丁希仑. 剪式单元可展机构静力学分析与拓扑优化设计[J].中国机械工程，2010，21 (2)：184-189.YANGYi,DINGXilun.AnalysisandTopologyOptimizationofDeployableMechanismBasedonPantograph[J] .ChinaMechanicalEngineering, 2010，21 (2):184-189.

[2] 刘成颖，谭锋，王立平，等.面向机床整机动态性能的立柱结构优化设计研究[J].机械工程学报，2016，52(3)：161-168.LIUChengying,TANFeng,WANGLiping,etal.ResearchonOptimizationofColumnStructureDesignforDynamicPerformanceofMachineTool[J].JournalofMechanicalEngineering, 2016，52(3):161-168.

[3] 周明刚，张露，陈源，等. 基于灵敏度分析的船式拖拉机机架结构优化设计[J].农业工程学报，2016，32(12)：54-59.ZHOUMinggang,ZHANGLu,ChenYuan,etal.StructuralOptimizationforRackofBoat-typeTractorBasedonSensitivityAnalysis[J].TransactionsoftheChineseSocietyofAgriculturalEngineering, 2016,32(12):54-60.

[4] 罗文豹，李维嘉，汪潇，等. 一种三自由度运动平台机构的优化设计[J].中国机械工程，2011，22 (14)：1728-1731.LUOWenbao,LIWeijia,WANGXiao,etal.MechanismOptimizationDesignfor3 -DOFMotionPlatform[J].ChinaMechanicalEngineering, 2011，22 (14):1728-1731.

[5] 曹红娟. 基于ANSYS的机架结构的优化设计[J]. 强度与环境，2013，40(6)：7-11.CAOHongjuan,AStudyaboutThrustFrameOptimumStructuralDesignwithANSYS[J].Structure&EnvironmentEngineering, 2013，40(6)：7-11.

[6] 李晓舟，龙志伟，邢向飞.基于MATLAB的异形片刹车机构的多目标优化设计[J]. 机械传动，2012，36(3)：55-58.LIXiaozhou,LONGZhiwei,XINGXiangfei.Multi-objectiveOptimizationDesignofShapedPieceBrakeMechanismBasedonMATLAB[J].JournalofMechanicalTransmission, 2012，36(3)：55-58.

[7] 李治多，王明强. 多工况载荷下连续体结构拓扑优化设计研究[J]. 现代制造工程，2008(9)：69-73.LIZhiduo,WANGMingqiang.ResearchonTopologyOptimizationDesignforContinuumStructureswithMultipleLoadCases[J].ModernManufacturingEngineering，2008(9)：69-73.

[8]ROYR,HINDUJAS,TETIR.RecentAdvancesinEngineeringDesignOptimisation:ChallengesandFutureTrends[J].CIRPAnnals—ManufacturingTechnology, 2008, 57(2):697-715.

[9] 何祯，宗志宇，孔祥芬.改进的满意度函数法在多响应优化中的应用[J].天津大学学报，2006，39(9)：1136-1140.HEZhen,ZONGZhiyu,KONGXiangfen.ApplicationofImprovedDesirabilityFunctionMethodtotheMulti-responseOptimization[J].JournalofTianjinUniversity， 2006，39(9):1136-1140.

[10] 陈羽，滕弘飞.产品设计耦合分析研究进展[J].计算机集成制造系统，2011，17(8)：1729-1736.CHENYu,TENGHongfei.AdvancesofCouplingAnalysisforProductDesign[J].ComputerIntegratedManufacturingSystems, 2011，17(8)：1729-1736.

[11] 李爱平，许静，刘雪梅. 基于设计结构矩阵的耦合活动集求解改进算法[J]. 计算机工程与应用，2011，47(17)：34-37.LIAiping,XUJing,LIUXuemei.ImprovedAlgorithmforCoupledActivitySetAnalysisBasedonDesignStructureMatrix[J].ComputerEngineeringandApplications, 2011，47(17)：34-37.

[12] 王忠宾，赵啦啦，李舒斌，等. 支撑掩护式液压支架的优化设计[J].重庆大学学报(自然科学版)，2009，32(9)： 1037-1042.WANGZhongbin,ZHAOLala,LIShubin,etal.OptimizationDesignforHydraulic-supportofStandingShield[J].JournalofChongqingUniversity(NaturalScienceEdition) ，2009，32(9):1037-1042.

[13] 何文斌，李菊丽，李立伟.ANSYS在液压支架优化设计中的应用[J]. 机械设计与制造，2007(6):170-172.HEWenbin,LIJuli,LILiwei.ApplicationofANSYSonDesignOptimizationofHydraulicPoweredSupport[J].MachineryDesign&Manufacture，2007(6):170-172.

(编辑 苏卫国)

Multi-objective Collaborative Optimization Method for Mechanical Systems Based on Coupling Analysis and Weighted Satisfaction Degree

MA Jun WU Liuyang HE Wenbin MING Wuyi CAO Yang

School of Mechanical and Electrical Engineering,Zhengzhou University of Light Industry， Zhengzhou，450002

Aiming at the mechanical system optimization result reliability problems caused by design variables coupling relation, based on weighted degree of satisfaction and coupling relation, a mechanical system multi-objective collaborative optimization method was proposed. At first, the coupling model for design variables of mechanical systems was established. And then, using maximum-minimum satisfaction function, considering sub-objective weighting factors, a weighted multi-objective collaborative optimization evaluation function was build. At last, the applications of mechanism-structure multi-objective collaborative optimization design of shield type hydraulic support four-bar prove the method may simplify optimization solution processes and improve the optimization result reliability.

multi-objective optimization; coupling relation; satisfaction degree; shield type hydraulic support

2016-08-22

国家自然科学基金资助项目(U1404621)；河南省高等学校青年骨干教师资助计划资助项目(2015GGJS-183);河南省科技攻关计划资助项目(162102210053)

TH165

10.3969/j.issn.1004-132X.2017.13.010

马 军，男，1977年生。郑州轻工业学院机电工程学院教授、博士。主要研究方向为大批量定制、模块化设计和PDM/PLM。发表论文20余篇。E-mail:78983836@qq.com。武柳洋，男，1988年生。郑州轻工业学院机电工程学院硕士研究生。何文斌(通信作者)，男，1970年生。郑州轻工业学院机电工程学院教授。E-mail:hwb@zzuli.edu.cn。明五一，男，1981年生。郑州轻工业学院机电工程学院讲师、博士。曹 阳，女，1987年生。郑州轻工业学院机电工程学院讲师、博士。