基于三维接触的滑环式旋转组合密封性能主控因素分析

祝效华 敬 洋

西南石油大学机电工程学院，成都，610500



基于三维接触的滑环式旋转组合密封性能主控因素分析

祝效华 敬 洋

西南石油大学机电工程学院，成都，610500

密封圈二维有限元分析中，常将密封圈接触面上最大接触压力推广到整个接触面上，针对这种不够精确的方法，提出了一种基于三维仿真模型的有效接触压力高精度计算方法。建立组合密封圈的三维模型，模拟实际工况，对影响其动密封特性的轴往复运动速度、轴转速、介质压力、O形圈压缩量、滑环厚度、滑环动接触面开槽进行了研究，并利用有效接触压力计算方法分析了动接触面上有效接触压力的分布情况。结果表明：滑环开槽、滑环厚度、O形圈压缩量以及介质压力对组合密封圈有效接触压力影响较大，内轴往复速度以及转速达到一定值后对有效接触压力影响较大。研究结果为滑环式组合密封圈的优化设计提供了参考。

组合密封；有效接触压力；有限元分析；主控因素分析

0 引言

在橡胶密封圈的计算中，由于涉及固体力学、摩擦学、高分子材料学、机械制造工艺学以及液体侵蚀等多方面的理论知识，因而对其变形、接触压力等问题的计算存在较大难度。有限元方法已被成功应用于橡胶密封圈的性能分析中，取得了较理想的分析效果[2-10]。谭晶等[1,11]研究了静密封状态下二维组合密封圈在不同因素影响下的接触应力、剪切应力分布规律，以及滑环厚度对各个密封面接触压力的影响规律。黄中华等[12]建立了O圈的二维模型并进行了仿真计算，得出O圈在深海高压下的接触压力分布规律，以及O圈压缩量对接触压力的影响规律。MAO等[13]研究了二维组合密封圈在变压力比与变往复速度下的接触压力分布规律，并探讨了介质压力、流速、往复杆速度等与组合密封圈泄漏之间的关系，得出了往复杆速度在0.1～0.4 m/s时，速度对往复杆内行程的影响大于外行程等结论。赵河明等[14]研究了O圈在三维动密封条件下的旋转运动，总结出了O圈的接触压力分布规律。

1 有效接触压力计算方法

目前，大多数研究只局限于静密封以及二维模型下的有限元分析，或只研究动密封中往复运动和旋转运动的一种，几乎没有对复合运动(轴同时进行往复运动和旋转运动)进行研究，并且很少扩展到三维模型的仿真计算。在三维模型中对复合运动的组合密封圈进行研究，存在如工作量大、计算时间长、仿真分析难度较高等难点。在二维模型中对密封圈接触压力进行研究时，一般把二维密封线的接触压力直接推广到整个接触面，默认整个接触面的接触压力是沿周向均匀分布，但在实际情况中，密封圈接触面上的接触压力分布并不完全是均匀分布[10-14]。滑环式组合密封圈简图见图1，图2为O圈密封及滑环组合密封中O圈及滑环的接触压力云图，从图2中可以看出，滑环内圈的接触压力沿周向非均匀分布，O圈的接触压力沿周向均匀分布。

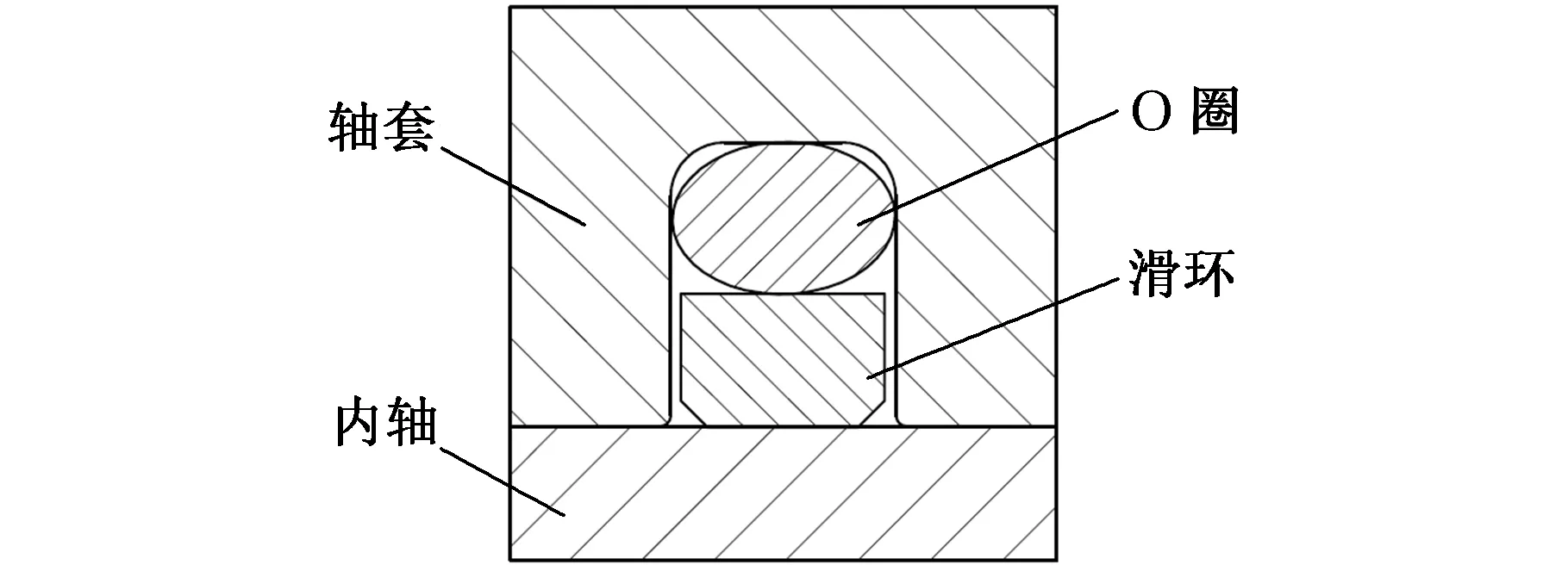
图1 组合密封圈二维示意图Fig.1 The 2D sketch of the combined seal

图2 O圈与滑环接触压力分布云图Fig.2 The contact pressure nephogram of the slip ring and O-ring

本文探讨组合密封圈的接触压力时，把滑环与内轴接触面(主密封面)沿轴向细分为无数条轴线，不同轴线都同时存在一个不同的最大接触压力值，如图3所示，其中轴线h上的最大接触压力值为所有轴线中最小的最大接触压力值，选择此接触压力值作为有效接触压力值(ECS)，其表达式为

pk=max(pi)

pe=min(pk)

式中，k为滑环密封面的任意一条轴线；i为任意一条轴线上的任意一点；pi为轴k上i点的接触压力值；pk为轴线k上的最大接触压力值；pe为有效接触压力值。

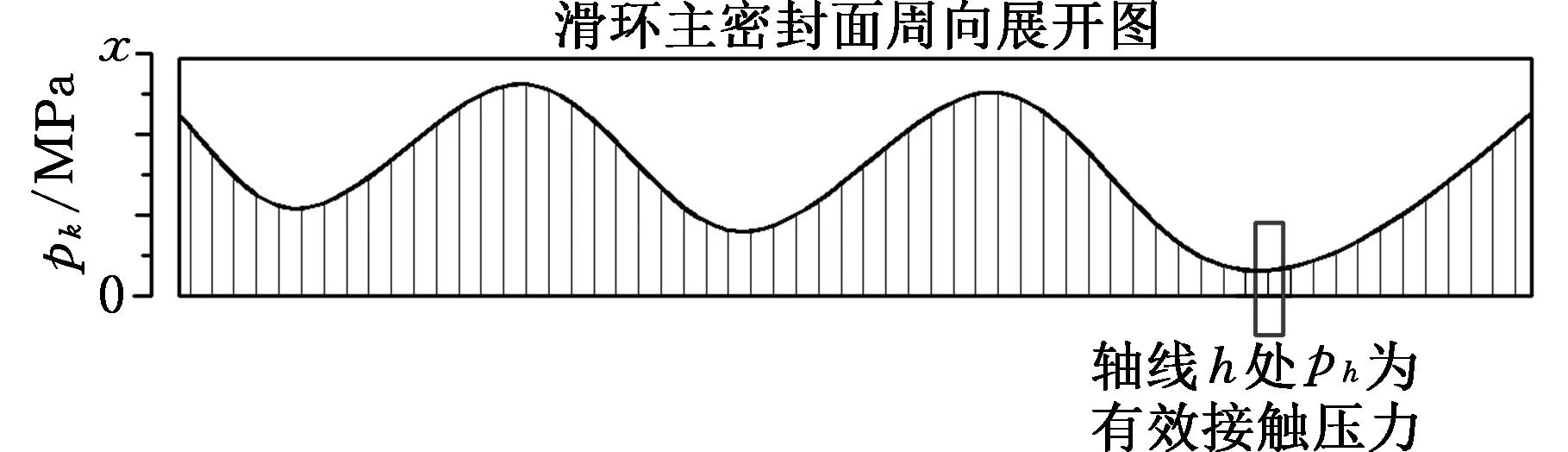
图3 有效接触压力示意图Fig.3 The sketch of the effective contact stress

2 有限元模型

2.1 材料模型

组合密封圈包含轴套、O圈、滑环、内轴4个部分。内轴的材料为40CrNiMo，弹性模量为209 GPa、泊松比为0.295、密度为7.87×103kg/m3；轴套材料为钢，弹性模量为209 GPa、泊松比为0.269、密度为7.89×103kg/m3；滑环材料为改性的聚四氟乙烯，弹性模量为960 MPa、泊松比为0.45、密度为2.32×103kg/m3。轴套沟槽尺寸采用国标GB/T 3452.3-2005。

O圈材料选用丁腈橡胶，截面直径取5.3 mm。由于橡胶为不可压缩的超弹性材料，确定弹性体材料的非线性特性是非常困难的，但基于应变能密度函数理论，用于弹性大变形的几种本构模型能准确模拟橡胶材料的力学性能；因此本文橡胶本构关系选用基于应变能密度函数的Mooney-Rivlin模型，其函数表达式为[10]

W﹙I1,I2﹚=C10﹙I1-3﹚+C01﹙I2-3﹚

σ=∂W/∂ε

式中，C10、C01为Rivlin系数，均为正定常数，本文O圈材料为丁腈橡胶，分别取1.87和0.47；I1、I2分别为第一、第二应变张量不变量。

2.2 有限元分析模型

图4 有限元计算三维仿真模型Fig.4 The 3D simulation model of finite element calculation

建立组合密封圈的三维仿真模型，赋予材料属性，建立接触对，并对相关零件进行网格划分,O圈采用杂交单元，滑环采用非协调单元，划分完成后的网格模型如图4所示。为了方便三维组合密封圈的装配，将沟槽(轴套)分为A部分和B部分，不影响对组合密封圈的有限元分析结果。整个分析分为4步：模拟组合密封圈的预压缩过程、介质工作压力加载过程、内轴往复运动过程以及旋转运动过程。

为了验证网格的独立性，分析网格划分大小对计算结果的影响，分别对组合密封圈划分近似全局尺寸为0.4、0.6、0.8的网格，并进行预装配仿真计算,网格如图4所示。计算得到的O圈最大接触压力分别为6.05 MPa、5.97 MPa、5.09 MPa。可以看出全局尺寸为0.6与0.8的网格O圈最大接触压力相差约17%，较大的网格仿真计算的结果存在较大的误差；而全局尺寸为0.4与0.6的网格O圈最大接触压力相差仅1%，可以认为几乎相等，但是过小的网格尺寸将使计算时间成倍的增加，所以全局尺寸选择0.6最合理。

由于橡胶密封问题存在几何非线性、材料非线性和接触非线性问题，所以在分析中做出以下几项假设：①模型材料具有确定的弹性模量和泊松比，并且各向同性；②忽略橡胶材料的应力松弛及蠕变特性；③在仿真过程中，忽略滑环的磨损。

3 仿真模型与计算方法验证

结合Kim等[15-16]在研究压缩O圈的相关实验与理论结果,建立与其相同尺寸规格的O圈(截面尺寸7 mm、内径128.5 mm)三维仿真模型，并施加与实验条件相同的O圈压缩率(20%)和边界条件后，进行数值模拟计算。利用有效接触压力计算方法计算O圈密封接触面的最大接触压力，研究在相同工况下密封面有效接触压力在不同介质压力下的变化规律。

图5 仿真结果与文献[15]实验理论结果对比Fig.5 The simulated results & comparison with the reference

通过有效接触压力计算方法计算出有效接触压力值，并与文献[15]的理论值及实验值相对比。由图5得出，数值模拟的计算结果与实验结果和理论计算结果的变化趋势基本一致，吻合度较高；仿真值基本处于实验值与理论值之间，与实验值差异很小，在5%以内；随着介质压力的升高，三者之间的差异在逐渐缩小。对比结果验证了本文有效接触压力计算方法具有较高的计算精度，也说明了本文采用的三维仿真计算方法具有较高的可靠性。

4 有限元计算结果

在组合密封圈工作时，总共有3个面与内轴和轴套接触，滑环与内轴的接触称为主密封面，也是动密封面。由于本文探讨的是复合运动状态下的组合密封特性分析，故只对主密封面进行密封性能研究。

4.1 O圈压缩量对组合密封圈密封性能的影响

在组合密封中对O圈进行压缩，主要有两个作用：①压缩的O圈给予滑环压力，达到密封的作用;②当滑环被磨损后，压缩的O圈产生的径向压力使滑环紧贴轴面，达到密封补偿作用。在仿真计算中，O圈压缩量a分别取0.5 mm、0.7 mm、0.9 mm、1.1 mm、1.3 mm，往复速度为0.3 m/s、转速为150 r/min、滑环厚度为2.5 mm、介质压力为25 MPa。

计算结果如图6所示。在所有压缩量下有效接触应力值不低于介质压力25 MPa，能保证密封。有效接触压力随着压缩量的增大而增大，这是因为压缩量越大，滑环受到O圈的压紧力也越大，导致有效接触压力值增大。当压缩量a=0.5 mm时，主密封面的有效接触压力值在下行程的0.05 s时有极小值30.32 MPa，仅仅比介质压力25 MPa高5.32 MPa；压缩量a在0.7～1.3 mm范围时，有效接触压力值在39 MPa左右波动，其中压缩量为0.9 mm及1.1 mm的有效接触压力值较0.7 mm

图6 变压缩量有效接触压力曲线Fig.6 The ECS curve with varying compression

及1.3 mm更平稳，更应该在设计中被考虑。

4.2 滑环厚度对组合密封圈密封性能的影响

不同的滑环厚度值对组合密封圈的密封性能有决定性的影响。在仿真计算中，滑环厚度b分别设计为2 mm、2.25 mm、2.5 mm、2.75 mm，往复速度为0.3 m/s、转速为150 r/min、压缩量为1.3 mm、介质压力为25 MPa。

计算结果如图7所示。有效接触压力随着滑环厚度的增大而减小，并且有效接触压力均大于介质压力，能够保证密封。这是因为随着滑环厚度的增加，滑环刚度增大，而有效接触压力随着滑环刚度的增大而减小。当滑环厚度b=2.75 mm时，最小有效压力值只有34 MPa，仅比介质压力高9 MPa。当b=2 mm时，有效接触压力值大约为48 MPa，密封可靠性较高，但滑环过薄，密封寿命较短。综上，滑环厚度在2.75 mm以下时，均能保证密封，但过大或过小的厚度值均不利于密封的可靠性，在设计中中间值更应该被考虑。

图7 变滑环厚度有效接触压力曲线Fig.7 The ECS curve with varying thickness

4.3 滑环开槽对组合密封圈密封性能的影响

密封圈在一些特殊的应用场合中，介质中可能会存在一些杂质成分(如钻井岩屑)，这些杂质一旦进入密封的动接触面，将会造成密封泄漏甚至于失效，在密封面开槽可以有效解决这个问题。开槽的主要作用如下：①沟槽内可以存储润滑油，有利于动密封面形成润滑油膜，减轻磨损；②即使有微小杂质进入，沟槽可以包住杂质，防止其对密封结构造成损伤。

在滑环与内轴的接触面上，设计两个均匀排列的半圆形槽，半径取0.3 mm，如图8所示。取往复速度0.3 m/s、转速150 r/min、压缩量1.3 mm、滑环厚度2.5 mm、介质压力25 MPa进行仿真计算。

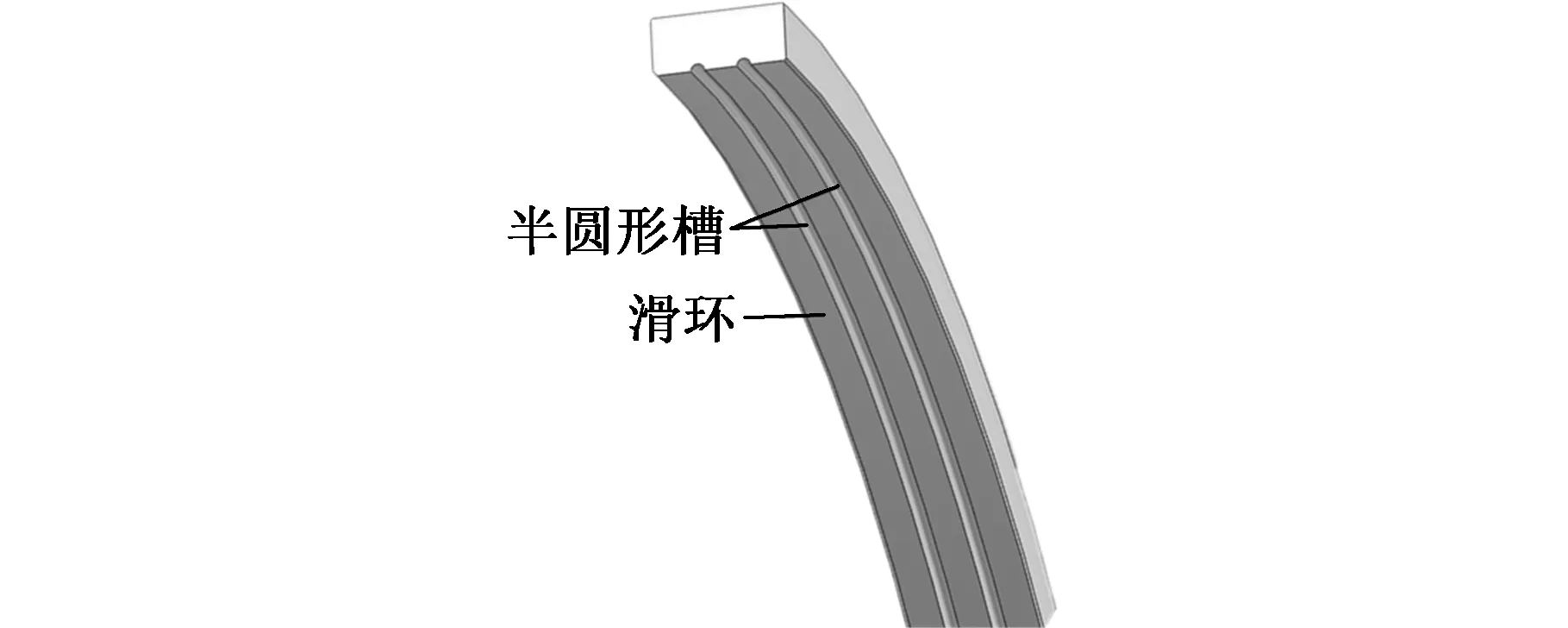
图8 开槽示意图Fig.8 The slotting sketch

计算结果如图9所示。开半圆形槽的有效接触压力值大约为75 MPa，比不开槽的有效接触压力大87.5%，表明开槽对有效接触压力影响很大。这是因为开槽会使接触面积减小，在滑环压紧力不变的情况下，密封面接触压力肯定会增大。

图9 开槽对有效接触压力的影响Fig.9 The influence of slotting on the ECS

4.4 转速对组合密封圈密封性能的影响

转速是影响动密封密封性能的重要参数，转速n分别取100 r/min、125 r/min、150 r/min、175 r/min、200 r/min，取往复速度0.3 m/s、压缩量1.3 mm、滑环厚度2.5 mm、介质压力25 MPa进行仿真计算。

计算结果如图10所示。在所有转速下有效接触压力值不低于介质压力25 MPa，能保证密封。在转速低于175 r/min时，组合密封圈滑环主密封面的有效接触压力在43 MPa左右小幅度波动，但随着转速的进一步增大，有效接触压力值开始出现比较大的波动。这是因为当转速增大到一定程度之后，滑环与内轴的接触状态没有低转速稳定，转速越高，接触压力会波动的越剧烈。综上，当转速低于175 r/min时，组合密封圈能与内轴较稳定的接触，有利于密封圈寿命的延长。

图10 变转速有效接触压力曲线Fig.10 The ECS curve with varying rotating speed

4.5 往复速度对组合密封圈密封性能的影响

旋转组合密封多是应用于往复运动的动密封场合中。往复速度v分别取0.1 m/s、0.2 m/s、0.3 m/s、0.4 m/s、0.5 m/s，取转速150 r/min、压缩量1.3 mm、滑环厚度2.5 mm、介质压力25 MPa进行仿真计算。

计算结果如图11所示。所有速度下的有效接触应力均大于介质压力25 MPa，能保证密封。在速度为0.1～0.4 m/s时，有效接触压力保持在42.5 MPa的水平小幅度波动；当速度达到0.5 m/s时，即内轴下行程开始时，有效接触应力值突然达到60 MPa以上，与之前的均值42.5 MPa相比波动量达到41%，并且在下行程的0.1 s之内出现反复波动；此外，当速度为0.5 m/s时，上行程过程中有效接触压力波动较小，只有下行程中有效接触压力值发生剧烈波动，所以速度对下行程的影响更大。这是因为在内轴往复运动速度方向改变时，滑环与内轴接触处变形方向的改变所致。综上，当往复速度低于0.5 m/s时，组合密封圈能与内轴较稳定的接触，有利于密封圈寿命的延长。

图11 变往复速度有效接触压力曲线Fig.11 The ECS curve with varying reciprocating speed

4.6 介质压力对组合密封圈密封性能的影响

本文研究单作用介质压力对组合密封圈的影响。介质压力分别取10 MPa、20 MPa、30 MPa、40 MPa、50 MPa，取往复速度0.3 m/s、转速150 r/min、压缩量1.3 mm、滑环厚度2.5 mm进行仿真计算。

图12 变介质压力有效接触压力曲线Fig.12 The ECS curve with varying medium pressure

计算结果如图12所示。不同介质压力作用的情况下，有效接触压力均大于介质压力，能够保证密封；并且有效接触压力随着介质压力的增大而增大，体现了组合密封圈自密封性能良好的特性；同时在介质压力增大时，有效接触压力增大的趋势在上升。在仿真的0.2 s过程中，上行程的有效接触压力与下行程的有效接触压力基本一致，只是在上行程和下行程的临界点，出现了有效接触压力的波动，这是因为接触面变形方向改变所致。

5 结论

(1)提出一种基于三维仿真模型的有效接触压力计算方法，避免了传统二维模型中简单地将一条轴线上最大接触压力推广到全部接触面上的不精确做法。

(2)随O圈压缩量a的增大，有效接触压力增大，其中a=0.9 mm和a=1.1 mm时有效接触压力值更平稳。往复运动速度在0.1～0.4 m/s时，有效接触压力整体平稳，上升到0.5 m/s时，出现较大波动。转速在100～150 r/min时，有效接触压力整体平稳，上升到175 r/min时，出现较大波动。随着滑环厚度的增大，有效接触压力减小；过大或过小的厚度值均不利于密封的可靠性，在设计中取中间值更合理。滑环开槽可有效增大有效接触压力，以及提高密封可靠性。

[1] 谭晶，杨卫民，丁玉梅，等.滑环式组合密封件的研究(Ⅰ)——方形同轴密封件(格来圈)的分析[J].润滑与密封，2007，32(1)：53-55. TAN Jing，YANG Weimin，DING Yumei，et al. The Study of a Sliding Ring Combined Seal Ring(Ⅰ)—The Analysis of Rectangle Co-Axia Seal[J].Lubrication Engineering，2007，32(1)：53-55.

[2] FRÖLICH D，MAGYAR B，SAUER B. A Comprehensive Model of Wear, Friction and Contact Temperature in Radial Shaft Seals[J].Wear，2014，311(1/2)：71-80.

[3] 陈国定，HAISER H，HAAS W，等.O形密封圈的有限元力学分析[J].机械科学与技术，2000，19(5)： 740-742. CHEN Guoding，HAISER H，HAAS W，et al. Analysis of Elastomeric O-ring Seals Using the Finite Element Method[J].Mechanical Science and Technology，2000， 19(5)：740-742.

[4] FIRED I，JOHONSON A R. Nonlinear Computation of Axisymmetric Solid Rubber Deformation[J].Computer Methods in Applied Mechanics and Engineering，1998,67(2)：241-253.

[5] NIKAS C K. Elastohydrodynamics and Mechanics of Rectangular Elastomeric Seals for Reciprocating Piston Rods[J]. Journal of Tribology，2003,125(1)：60-69.

[6] GEORGE K, NIKAS C K, RICHARD S，et al. Computational Model of Tandem Rectangular Elastomeric Seals for Reciprocating Motion[J].Tribology International，2006，39 (1)：622-634.

[7] PROKOP J，MULLER H K. Film Thickness, Contact Pressure and Friction of PTFE Rod Seals[C]//12th International Conference on Fluid Sealing. Brighton,1989:147-163.

[8] SLALANT R F，MASER N，YANG B. Numerical Model of a Reciprocating Hydraulic Rod Seal[J]. Journal of Tribology, 2007，129(1)：91-97.

[9] RUSKELL L E. A Rapidly Converging Theoretical Solution of the Elastohydrodynamic Problem for Rectangular Rubber Seals[J]. Journal of Mechanical Engineering Science，1980，22(1)：9-16.

[10] 王伟，赵树高.橡胶O形密封圈的接触变形及应力分析[J].弹性体，2005，15(4)：28-31. WANG Wei，ZHAO Shugao. Analysis on Contact Deformation and Stress for Rubber O-sealing Ring [J].China Elastomerics，2005，15(4)：28-31.

[11] 谭晶，杨卫民，丁玉梅，等.O形橡胶密封圈密封性能的有限元分析[J].润滑与密封，2006(9)：65-69. TAN Jing，YANG Weimin，DING Yumei，et al. Finite Element Analysis of the Sealing Performance of O-ring Seal Structure[J]. Lubrication Engineering，2006(9)：65-69.

[12] 黄中华，金波，刘少军.深海高压舱密封性能评价研究[J].浙江大学学报(工学版)，2007，41(5)：790-793. HUANG Zhonghua，JIN Bo，LIU Shaojun. Sealing Performance Evaluation of Deep Sea High Pressure Cabin[J].Journal of Zhejiang University(Engineering Science)，2007，41(5)：790-793.

[13] MAO J F，WANG W Z，LIU Y Z. Experimental and Theoretical Investigation on the Sealing Performance of the Combined Seals for Reciprocating Rod [J].Journal of Mechanical Science and Technology，2012，26(6)：1765-1772.

[14] 赵河明，韩宁.动态压力下旋转动密封结构有限元分析[J].现代制造工程，2014(10)：81-85. ZHAO Heming，HAN Ning. Finite Element Analysis of Rotary Sealing of O-ring[J].Modern Manufacturing Engineering，2014(10)：81-85.

[15] KIM H K，NAM J H，HAWONG J S，et al. Evaluation of O-ring Stresses Subjected to Vertical and one Side Lateral Pressure by Theoretical Approximation Comparing with Photo Elastic Experimental Results[J]. Engineering Failure Analysis，2009,16(6)：1876-1882.

[16] KIM H K，PARK S H，LEE H G，et al. Approximation of Contact Stress for a Compressed and Laterally One Side Restrained O-ring[J].Engineering Failure Analysis，2007,14(8)：1680-1692.

(编辑 袁兴玲)

Analysis of Main Influence Factors for Slip Ring Combined Rotating Seals Based on 3D Contact

ZHU Xiaohua JING Yang

School of Mechanical Engineering, Southwest Petroleum University, Chengdu, 610500

The calculation which applied the traditional 2D FEA to generalize the maximum contact stress on a single-contact line of the sealing ring to the whole contact surface was not an accurate algorithm. In view of it, a more accurate and effective contact stress calculation method was proposed based on the 3D simulation model herein. Some different 3D models of the combined sealing ring were established through simulating the actual working conditions, and the method was used to analyze the effective contact stress distribution under the different effect factors of the dynamic seal characteristics, such as the reciprocating motion speeds, the revolving speeds, the medium pressures, the O-ring compressions, the thicknesses of the slip rings and the slottings on the moving contacts. The results show that the slottings on the moving contacts, the thicknesses of the slip ring, the O-ring compressions and the medium pressures have a great influence on the values of effective contact stresses; when the reciprocating motion speeds and the revolving speeds of inner shaft exceed a critical value, they have an influence on the values of the effective contact stresses. The results of this paper provide a reference for the optimization design of slip ring combined seals.

combined seal; effective contact stress; finite element analysis(FEA); analysis of main influence factor

2016-09-07

国家自然科学基金资助项目(51674214)；四川省青年科技创新研究团队资助项目(2017TD0014)；四川省科技计划国际合作计划项目(2016HH0008)

TH136

10.3969/j.issn.1004-132X.2017.13.006

祝效华，男，1978年生。西南石油大学机电工程学院教授、博士研究生导师。主要研究方向为管柱力学和钻井提速等。E-mail:zxhth113@163.com。敬 洋，男，1992年生。西南石油大学机电工程学院硕士研究生。