带软时间窗的冷链物流配送路径优化研究

俞武扬，杨沈记

（杭州电子科技大学 管理学院，浙江 杭州 310018）

带软时间窗的冷链物流配送路径优化研究

俞武扬，杨沈记

（杭州电子科技大学 管理学院，浙江 杭州 310018）

消费者对生鲜产品的需求不断增加，促进了城市冷链物流的快速发展。文章分析了冷链车的能耗成本和货损成本，并将运输过程和卸货过程分开进行考虑，以总成本最低为目标建立了带软时间窗的优化模型。针对具体模型特点设计遗传算法进行求解，最后结合具体实例进行仿真试验，遗传算法所得配送线路方案比原有扫描法配送方案成本明显更低，从而验证了模型和算法的有效性。

冷链物流；路径优化；软时间窗；遗传算法

一、引言

消费者对生鲜产品的需求不断增加，促进了城市冷链物流的快速发展。据《2015中国冷链物流发展报告》所述，我国冷链物流总需求量已经连续三年超过15%的增长率，按此趋势估计，城市冷链物流发展空间巨大。冷链物流是指冷藏冷冻类生鲜产品在物流过程（包括生产、存储与运输配送等环节）中始终处于规定低温环境，从而保证产品品质的特殊物流[1]。冷链物流配送问题是在著名学者Dantzig和Rasmer[2]提出的车辆路径问题（Vehicle Routing Problem，VRP）的基础之上，结合时间窗约束、能耗成本和货损成本等因素构建而成。

本文研究的就是冷链物流的路径优化问题，目前对该方面的研究，国内外诸多学者已取得了一系列相应成果：在国外，Lidija Zadnik等[3]研究了带时间窗约束的农产品冷链配送优化问题；Pedro Amorim等[4]研究了葡萄牙食品配送VRP问题，但是研究过程中没有考虑货损的因素；J Brito等[5]研究了在不确定时间分布情况下冷冻食品的模糊车辆路径问题，通过软计算方法得到最优解；近年来，由于城市交通状况复杂度越来越高，城市生鲜食品配送运输条件越发严峻，导致末端各种问题不断显现，Song BD，Ko YD等[6]研究了城市易腐食品的末端配送问题，在配送需求位置与数量已知，配送供应中车辆的数量与规格确定的情况下，以最优服务效率为目标研究了普通货车与冷藏车混合配送优化问题。在国内，李雅萍[7]研究了带时间窗的鲜活农产品冷链物流VRP成本模型；邵举平、曹倩等[8]为提高生鲜农产品物流配送效率，建立了最大化顾客满意度以及最小化配送成本的多目标优化模型，并设计了基于遗传算法的求解方法；姚宝珍等[9]在研究西餐厅连锁店的路径优化路线时，为满足各连锁店时间窗的约束建立了带时间窗的VRP模型，然后运用启发式算法对模型进行求解，并且用经典案例检验了算法性能，最后将文章提出的算法求解实际的大连市连锁西餐厅配送路线；葛显龙等[10]在VRP的基础上充分考虑配送损耗等因素建立带时间窗的生鲜损耗配送模型，针对模型的特征设计自适应的遗传算法对模型求解。

从目前的研究来看，学者们在生鲜农产品配送与车辆路径问题的结合进行了较多的研究，但对冷链物流的研究相对还不够完善；由于冷链物流配送所配送货物具有较强的易腐性，因而在配送的时效性方面要求比较高，并且还需要配备特殊的冷藏保鲜设备，因此决策过程所涉及的因素更加复杂多样，模型求解难度更大。本文将软时间窗加入到冷链物流配送中，考虑冷链车的能耗成本和货损成本，并将运输过程和卸货过程分开进行考虑，以总成本最低为目标建立数学模型，针对具体模型特点设计自适应遗传算法进行求解，最后结合具体实例进行仿真试验，并将优化后的冷链配送中心的配送线路方案与传统扫描法所得方案进行对比，从而验证算法和模型的有效性。

二、问题描述与模型构建

（一）问题描述

本文研究的带软时间窗冷链物流配送路径优化问题为：在给定区域内，一个冷链配送中心给若干客户进行冷链产品的配送服务，配送中心和客户的地理位置已知，不同客户的需求量和可接受的服务时间段存在差异，要求合理安排冷链车的配送路径使得货物能在客户可接受的时间段内到达，并使总配送成本最小。

为了简化研究问题，这里认为配送的冷链货品腐败率一致并且问题需满足以下约束假设：（1）配送中心拥有固定数量的冷链车，车辆车型一致；（2）所有的冷链车必须从配送中心发出并最终回到配送中心；（3）每位客户的需求量大于零且小于冷链车最大载重；（4）每位客户的需求必须得到满足且只能由同一辆车进行配送服务；（5）配送任务需要在客户指定时间段内完成；（6）客户点和配送中心的位置距离满足三角不等式；（7）不考虑交通拥堵等情况，配送过程中冷链车匀速行使；（8）配送中心货物充足，车辆每次配送任务不会出现超载情况；（9）配送过程中冷链车能够始终保持货品所需温度，车内温度不变；（10）不考虑货品在配送中心的装货时间及货损。

（二）模型构建

1.参数与变量设置。模型所需的参数与变量说明如表1所示：

表1 参数与变量说明

2.数学模型。根据问题的描述，带软时间窗的冷链物流配送路径优化的数学模型可表示为：

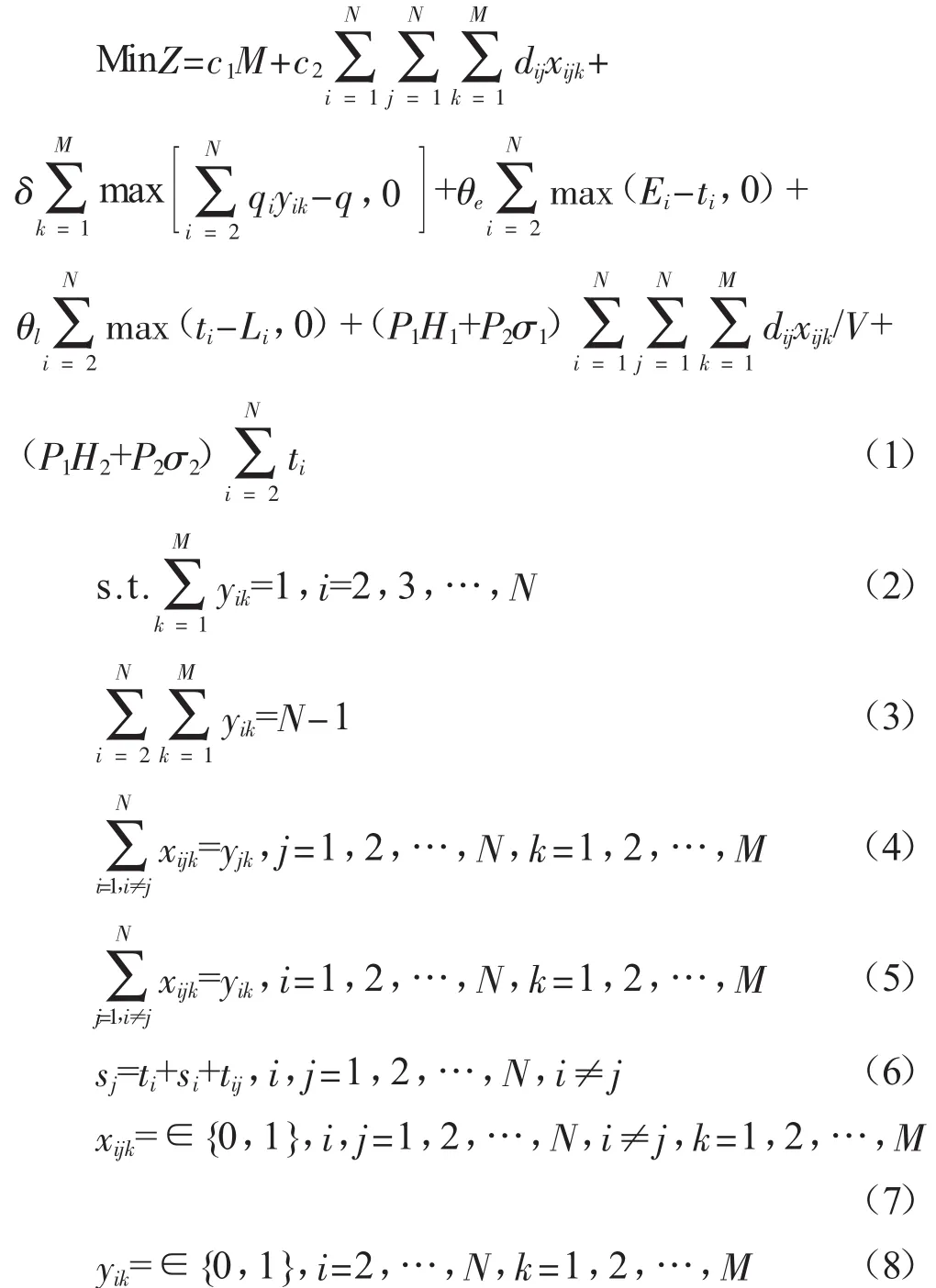
模型中的目标函数（1）表示的是：冷链车的固定成本、车辆行使的运输成本、超载惩罚成本、早到等待成本、晚到惩罚成本、运输过程中的能耗成本与货损成本、卸货过程的能耗成本与货损成本；约束（2）表示每个客户只能由一辆车配送；约束（3）确保配送任务覆盖所有客户；约束（4）、（5）表示变量之间的关系；约束（6）表示配送时间数量关系；约束（7）、（8）表示变量的定义。

三、算法设计

遗传算法是一种基于群体遗传进化机制的自适应全局优化算法。本文针对带软时间窗的冷链车辆配送问题特点设计了如下遗传算法。

（一）染色体编码

本文采用的是自然数编码方式进行编码，配送中心编号为1，冷链配送中心同时使用M辆冷链车给多个客户点（编号为2，3，…，N）进行冷藏商品配送，最后又回到配送中心。染色体长度为N+M+1，一条染色体表示一种配送方案，如染色体“128415631791”表示3辆冷链车给8个客户点（编号为 2，3，…，9）配送。路径 1：配送中心 1→客户2→客户8→客户4→配送中心1；路径2：配送中心1→客户5→客户6→客户 3→配送中心1；路径3：配送中心1→客户7→客户9→配送中心1。

（二）初始化染色体

本文设计了一种考虑每条路径中冷链车最大载重量限制的初始化染色体方法：

步骤1：染色体第一个基因位置设为配送中心1，然后给编号为2至N的N-1个客户点随机排序。

步骤2：从染色体基因1后的客户点开始遍历，对客户点需求量进行累计求和，如果冷链车的最大承载重量Q大于前s个客户点需求量之和且小于前s+1个客户点需求量之和，则在第s个客户点后插入配送中心基因1，并记录插入次数num。

步骤3：遍历染色体新插入基因1后面的客户点。也就是从第s+1个客户点起重新进行遍历操作，重复步骤2以获得第2条路径配送的客户点；如此反复安排所有客户点的配送路径。

步骤4：如果步骤3中新遍历的客户点总需求量小于最大承载重量Q，则直接在最后插入配送中心1，此时可得到一条初始染色体。

现有8个客户点的随机排序：“35786924”，如图1所示可得到一条初始染色体：“135178619241”。

图1 初始染色体生成示例

（三）交叉与变异算子

遗传算法中最具特色的机制即其中的交叉算子和变异算子，通过这两种算子实现了对生物进化的模拟。由于设计的编码含有多个配送中心基因“1”以及客户为自然数编码，普通的交叉及变异方式易产生不可行解，因此本文设计了如下保证可行性的两种算子：

（1）交叉算子：对于所选中的两个父代染色体，去除表示配送中心的基因项“1”后将它们还原成为关于客户2至N的两个排列，随机选中两个点位，由两个父代染色体生成两个子代染色体，各自继承父代中两点位之间的基因不变，而两点位外的基因则由另一个父代染色体排除已继承基因后依次填入空位即得，然后再利用初始化染色体的方法重新插入配送中心基因项“1”生成两个可行的子代染色体。该交叉过程示例如图2所示。

图2 交叉算子示例

（2）变异算子：对于选中的父代染色体，同样先去除表示配送中心的基因项“1”后还原成关于客户2至N的一个排列，然后随机选择其中两个基因进行互换，再利用初始化染色体的方法重新插入配送中心基因项“1”生成可行的子代染色体。

（四）其余条件

（1）适应度函数，适应度用于评价配送方案的好坏程度，染色体（即表示配送方案）适应度值越大，该配送方案保留下来的概率也越大。由于目标函数是求解总成本最小的配送方案，因此设定适应度函数f为目标函数Z的倒数，f=1/Z。

（2）选择机制，根据各个个体的适应度，按照轮盘赌方法从第t代种群P（t）中选择出优良的个体遗传到下一代种群P（t+1）中。

（3）算法终止条件，以事先给定的最大迭代次数作为算法终止条件。

四、实验与仿真分析

（一）实例描述

杭州某冷链配送中心拥有同一车型冷链车6辆，车辆最大载重为3.6吨，需要向周边区县的14个大型超市配送某种冷藏商品，根据前面建模数据，配送中心标号为1，其余14个客户点标号为2至15，配送中心和各客户点的位置坐标、客户点的需求信息、服务时间和时间窗约束均如表2所示。

表2 各客户点配送相关信息（#表示编号）

根据一般冷链配送标准，每辆冷链车完成一次配送任务平均固定成本C1为300元；冷链车行驶速度平均为50 km/h，每公里的运输成本为C2为3元/km；车门不开和车门打开时单位温差时单位时间发生的热负荷为 H1、H2分别为 60 kCal/h和80 kCal/h，单位热负荷产生的成本P1为0.4元/kCal；冷藏商品价格 P2为 12 000元 /t，车门关闭和车门开启时货损率分别为σ1=0.3%，σ2=0.5%。配送中心每天早上5点统一发货，从发货时间开始计算，冷链车从配送中心出发，最后又回到配送中心，选择使得总成本最小的配送路线方案。

（二）遗传算法优化方案

针对上面的实例数据，设定种群规模为NIND=100，算法迭代终止代数为MAXGEN=300，自适应交叉概率 Pc=0.7，变异概率 Pm=0.3，代沟 GGAP=0.9；超载惩罚系数设为δ=10000；提前到达等待成本系数为θe=400，迟到的惩罚成本系数为θl=500。根据算法结合MatlabR2014a编制程序共运行10次，其中有9次得到最优配送方案，平均配送距离为1 071.56 km，平均配送总成本为6 836.94元，平均计算时间为7.30秒。最优配送方案如下：使用5辆冷链车进行配送，总行驶距离为1 059.18 km，最优配送总成本为6 785.7元，求得最优配送路线方案如图3所示。

每个配送环路表示由一辆冷链车进行配送，最优方案有5条子路径，各子路径配送数据见表3。算法中染色体种群进化过程如图4所示，从图中曲线可知，在算法运行开始曲线下降速度较快表明算法寻优速度较快；随后曲线变化趋于缓和，种群中个体值逐渐开始收敛，最后在接近70代左右收敛到问题的最优解。

图3 最优配送路线方案

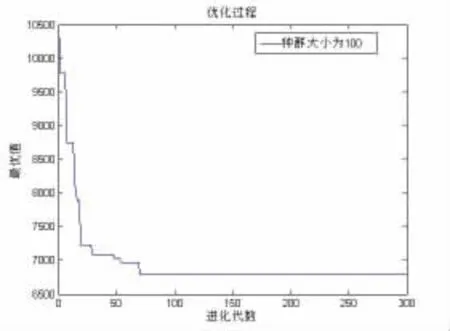
图4 遗传算法进化图

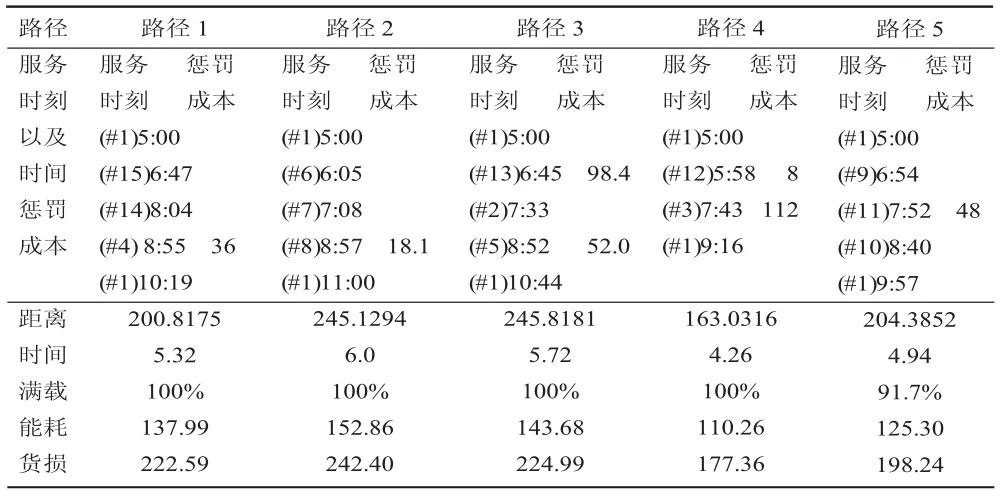
表3 最优配送方案各子路径数据

（三）扫描法优化方案

目前该冷链配送中心主要采用扫描法再结合客户点时间窗要求进行冷链车路径规划。具体操作方式如下：以冷链配送中心为中心点，再选取任意一个最早需配送的客户点为起始点，这里选取的是客户点9；沿这两点画一条射线顺时针方向旋转，以车辆容量为分群约束进行客户点的扫描分群，然后在每个分群考虑客户点的时间窗要求安排车辆配送的先后顺序，直到将所有客户点安排好路线。利用扫描法结合客户点时间窗要求，配送中心使用6辆冷链车进行任务配送，路线安排如图5所示。

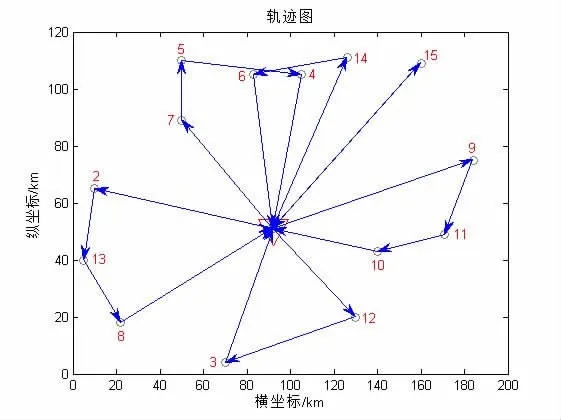
图5 配送中心利用扫描法进行路线规划的方案

扫描法所得配送方案总行驶距离为1 115.57 km，方案总成本为9 060.8元，各配送子路径数据如表4所示。

表4 配送子路径结果数据（扫描法）

（四）方案比较

目前大部分中小型配送企业主要是采用扫描法对配送路线进行安排规划，这种方法主要是注重对配送距离的考虑，对于有时间窗的配送任务很难考虑全面，如表5用扫描法安排带时间窗的配送任务往往会使得时间窗惩罚成本很高，最终总成本增加。本文设计的遗传算法在求解带软时间窗的冷链物流路径优化问题时能够同时考虑时间窗约束、运输总距离、冷链车能耗成本和货损成本，能够找到总配送成本最优的冷链车配送方案。两种方法相比较而言，遗传算法具有明显优势总成本节约了2 275.1元，从而验证了本文算法的有效性。

表5 优化结果比较

五、小结

本文研究了带软时间窗的冷链物流路径优化问题，在带时间窗VRP问题基础上考虑了冷链车的能耗成本和货损成本，并将运输过程和卸货过程分开进行考虑，建立了以总成本最低为目标的数学模型，针对具体模型特点设计了遗传算法进行求解，最后结合实例进行仿真试验。仿真结果表明，本文设计的算法在求解冷链物流路径优化问题时比扫描法具有明显优势，能够有效解决冷链物流路径优化问题。

[1]马向国，刘同娟，杨平哲，等，2016.基于随机需求的冷链物流车辆路径优化模型[J].系统仿真学报（8）：1824-1832.

[2]DantzigGB，Ramser J H.The Truck DispatchingProblem[J].Management Science，1959，6（1）：80-91.

[3]Osvald A，Stirn L Z.A vehicle routing algorithm for the distribution of fresh vegetables and similar perishable food[J].Journal of Food Engineering，2008，85（2）：285-295.

[4]Amorim P，Parragh S N，Sperandio F，et al.A rich vehicle routing problem dealing with perishable food：a case study[J].TOP，2014，22（2）：489-508.

[5]Brito J，Martinez F J，Moreno J A，et al.Fuzzy optimization for distribution of frozen food with imprecise times[J].Fuzzy Optimization and Decision Making，2012，11（3）：337-349.

[6]Song B D，Ko Y D.A vehicle routing problem of both refrigeratedand general-type vehicles for perishable food products delivery[J].Journal of Food Engineering，2016，169：61-71.

[7]李雅萍，2013.鲜活农产品冷链物流配送路径优化研究[J].价值工程（31）：25-27.

[8]邵举平，曹倩，沈敏燕，等，2015.生鲜农产品配送中带时窗的VRP模型与算法[J].工业工程与管理（1）：122-127.

[9]姚宝珍，杨成永，张强，等，2010蚁群算法在西餐连锁店配送路径中应用[J].北京交通大学学报（6）：51-55.

[10]葛显龙，孔阳，2016.带有时间窗的生鲜物流配送路径优化研究[J].数学的实践与认识（12）：78-87.

（责任编辑：D 校对：R）

F252.8

A

1004-2768（2017）06-0067-04

2017-03-22

浙江省哲学社会科学规划项目（17NDJC053YB）；教育部人文社会科学青年基金项目（13YJC630177）

俞武扬（1974-），男，博士，杭州电子科技大学管理学院副教授，研究方向：物流建模与优化计算、应急管理等；杨沈记（1992-），男，杭州电子科技大学管理学院硕士研究生，研究方向：物流配送优化。