旗传递4-(v,k,6)设计与Sz(q)群

赵 坤，温绍泉，邢志红，孙淑兰，李晓霞，赵裕亮

(佳木斯大学理学院，黑龙江 佳木斯 154007)

旗传递4-(v,k,6)设计与Sz(q)群

赵 坤，温绍泉，邢志红，孙淑兰，李晓霞，赵裕亮

(佳木斯大学理学院，黑龙江 佳木斯 154007)

设S=(P,B)是一个非平凡的4-(q2+1,k,6)设计，其中q=22n+1且为整数。如果G≤Aut(S)在S上区传递且Soc(G)同构于李型单群Sz(q)群，则G在S不是旗传递的。

区传递；旗传递；Sz(q)群；十二设计

对于正整数t≤k≤v及λ，我们定义一个t-(v，k，λ)设计是一个诱导结构S=(P，B)，其中P表示点集合且|P|=v，B表示区组集合且|B|=b，并且每个区组包含k个点，每一个P中的t-子集包含在λ个区组中。S的一个旗是指一个点—区组对(x，B)且x包含在区组β中，其中β∈B。设G≤Aut(S)。如果G在P上是传递的，则称G是点传递的；如果G在P上是本原的，则称G是点本原的；如果Aut(S)是点传递(点本原)的，则称S是点传递(点本原)的；如果G在B上是传递的，则称G是区传递的；如果G在B上是本原的，则称G是区本原的；如果Aut(S)是区传递(区本原)的，则称S是区传递(区本原)的。

设S=(P，B)是一个t-(v，k，λ)设计。一个对(p，β)被称为旗，如果p∈P，β∈B且p∈β。如果G≤Aut(S)在旗集合上是传递的，则称G是旗传递的。

对于任意的λ及较大的t的t-设计，Cameron和Praeger证明了随后的结论：

定理[1]设S=(P，B)是一个t-(v，k，λ)设计。如果G≤Aut(S)区传递作用在S上，则t≤7。如果G≤Aut(S)旗传递作用在S上，则t≤6。

目前Huber[2]利用2—传递置换群的知识完成了所有的旗传递Steinert-设计的分类。所以决定所有的λ≥2的t-设计的旗传递分类是一个长期且公开的研究问题。

在2010年，徐向红[3]完成了旗传递6-(v，k，λ)设计，其中λ≤5。同年，刘伟俊[4]完成了群PSL(2，q)上的旗传递5-(v，k，2)设计。2011年，徐向红[5]完成了两类Lie型单群与旗传递4-(v，k，2)设计的分类。本文研究了Sz(q)群与4-(v，k，6)设计的问题，最终得到了以下定理：

主要定理 设S=(P，B)是一个非平凡的4-(q2+1，k，6)设计，其中q=22n+1且n≥1为整数。如果G≤Aut(S)在S上区传递且Soc(G)同构于李型单群Sz(q)群，则G在S不是旗传递的。

1 预备引理

Suzuki群Sz(q)是属于李型单群家族，在文献[6-7]中被定义为SL(4，q)的一个子群。设GF(q)是一个q元素的有限域，其中q=22n+1且n≥1为整数(特别地，q≥8)。设Q是Sz(q)的Sylow 2-子群，K是有限域GF(q)的乘法群，于是Sz(q)是一个阶为q2(q2+1)(q-1)的群。因此，Sz(q)作为Steiner3-(q2+1，q+1，1)设计上的自同构群2-传递作用在q2+1个点上。

对于t-设计S=(P，B)且G≤Aut(S)，r表示通过给定点的区组数，Gx表示点x∈P的稳定化子，Gβ表示区组β∈B的稳定化子，我们定义Gxβ=Gx∩Gβ。

引理1[2]设G旗传递作用在t-(v，k，λ)设计S=(P，B)上，则G是2-传递的且下列结论成立：

1)|G|=|Gx||xG|=|Gx|v，其中x∈P;

2)|G|=|Gβ||βG|=|Gβ|b，其中β∈B;

3)|G|=|Gxβ||(x，β)G|=|Gxβ|bk，其中x∈β。

引理2[8]间设S=(P，B)是一个非平凡的t-(v，k，λ)设计，则

λ(v-t+1)≥(k-t+2)(k-t+1)。

引理3[8]间设S=(P，B)是一个非平凡的4-(v，k，λ)设计，则

1)bk=vr;

推论1 设S=(P，B)是一个非平凡的4-(v，k，6)设计，如果v=q2+1，则

证明:由引理2，我们有6(v-3)≥(k-2)(k-3)。如果v=q2+1，则

6(q2-2)≥(k-2)(k-3)，

即

k2-5k-6q2+18≤0，

于是

2 主要定理的证明

假设G在4-(v，k，6)设计上是旗传递的且v=q2+1，则G是2-传递的且点传递。既然T=Sz(q)≤G≤Aut(T)，可以由Dedekind定理得到G=T:〈α〉且G=T:(G∩〈α〉)，这里α:x→x2，x∈GF(q)且α是GF(q)的一个自同构。设q=2f，f=2n+1是奇数且|〈α〉|=m，于是m|f。显然|G|=q2(q2+1)(q-1)m。

首先我们将证明，如果g∈G能够稳定P中的3个点，则g必定至少稳定P中的5个点。

假设g∈G，|FixP(g)|≥3，x∈|FixP(g)|。设P是Gx的正规Sylow 2-子群，则P在P-{x}上是传递的。由于v=q2+1，我们得到|P|=|P-{x}|=q2。因此，P正则作用在P-{x}上，那么对任意的y，z∈P-{x}，存在点h∈P使得z=yh。既然g∈Gx，h∈P且P是Gx的正规Sylow 2-子群，我们有h-1ghg-1∈P。另一方面，

zh-1ghg-1=yghg-1=yhg-1=zg-1=z，

因此h-1ghg-1=1，即gh=hg。所以，h∈C=CP(g)。我们得到C在FixP(g)-{x}上是传递的。因此|FixP(g)-{x}|||C|。再由C≤P，得到|FixP(g)-{x}|||P|。我们注意到|P|=q2=22f，因此|FixP(g)-{x}||22f。最终|FixP(g)-{x}|≡0(mod 2)，即为|FixP(g)|≡1(mod 2)。

对所有的h∈CT(g)，y∈FixP(g)，我们有yhg=ygh=yh，因此yh∈FixP(g)，这意味着FixP(g)是一个区组且被CT(g)所稳定。由C≤CT(g)及C在Fixp(g)-{x}传递，我们得到CT(g)在Fixp(g)上也是传递的。因此|FixP(g)|||CT(g)|。另外，|CT(g)|||T|，因此|FixP(g)|||T|。显然，3不能整除|T|。因而|FixP(g)|≠3。再由|FixP(g)|≡1(mod 2)，我们得到|FixP(g)|≥5，这意味着g至少稳定P中的5个点。

现在我们继续证明主要定理。显然，α稳定P中的0，1，∞ 3个不同的点。因此〈α〉≤G0，1，∞，于是α至少稳定P中的6个点。既然G区传递在4-(v，k，6)设计上，我们找6个区组，β1，β2，β3，β4，β5及β6都是被α所稳定。如果α改变β1，β2，β3，β4，β5及β6，则2||〈α〉|，这是不可能的。因此α必定稳定β1，β2，β3，β4，β5及β6。我们有G∩〈α〉≤G0β1=G0β2=G0β3=G0β4=G0β5=G0β6，因此T旗传递作用在4-(q2+1，k，6)设计上，于是我们可以假定G=T且|G|=q2(q2+1)(k-1)。

既然G旗传递作用在4-(q2+1，k，6)设计上，由引理1，我们有

再由引理3及引理1，

因此

由引理2，

6|Gxβ|(q+1)(q2-2)=(k-1)(k-2)(k-3)≤(k-1)·6(v-3)=6(k-1)(q2-2)。

再由推论1，

因此|Gxβ|=1，既有

6(q+1)(q2-2)=(k-1)(k-2)(k-3)=k(k2-6k+11)-6，

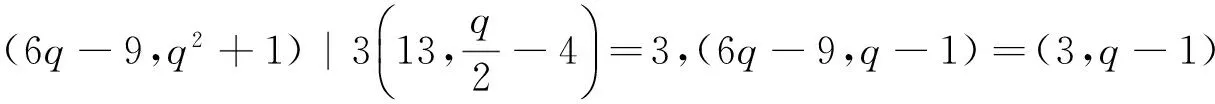
这样完成了主要定理的证明。

[1] Cameron P J，Praeger C E.Block-transitivet—designs，Ⅱ:large t，In F.DeClerck，et al.(Eds)，finite geometry and combinatorics[J].London Math.Soc.lecture Note Series，1993，(191):103-119.

[2] HuberM.Flag-transitive Steiner Designs[M].Berlin:Birkhausen Basel，Boston，2009.

[3] Xu Xianghong，Liu Weijun.On flag-transitive 6—(v，k，A)designs withA<5[J].ArsCombin，2010，97:507-510.

[4] Liu Weijun，Tan Qionghua，Gong Luozhong.Flag-transitive 5—(v，k，2)designs[J].Jiangsu Univ.，2010，31:612-615.

[5] Xu Xianghong，Zhao Lina，Liu Weijun.Two classes lie type simple groups and flag-transitive 4—(v，k，2)designs[J].Journal of Zhejiang Unviersity，2011，38:4-6.

[6] SuzukiM.A new type of simple group of finite order[J].Proc.Nat.Acad.Sci.U.S.A.，1960，46:868-870.

[7] Suzuki M.On a class of doubly transitive groups[J].Ann.of Math.，1962，75:105-145.

[8] Shen H.The theorey of combinatorial design[M].Shanghai：Shanghai Jiao Tong Univ.Press，1990.

The Design of Flag-transitive 4-(v，k，6)and Suzuki groups

ZHAO Kun，et al.

(DepartmentofMathematics，JiamusiUniversity，JiamusiHeilongjiang154007，China)

The design letS=(P，B) be a non-trivial 4-(q2+1，k，6)，in whichq=22n+1，andn≥1 as an integer.IfG≤Aut(S)acts block-transitively onSarea，andSoc(G) is isomorphic to the simple Lie typeSz(q)group，thenGis in not flag-transitive onSarea.

block-transitive；flag-transitive；Sz(q)group；t-design

2017-05-22

黑龙江省教育厅课题(12541829)

赵坤(1978-)，女(汉)，黑龙江佳木斯，讲师 主要研究常微分方程理论与应用。

10.3969/j.issn.1009-8984.2017.02.029

O152.1

A

1009-8984(2017)02-0126-03