基于小波变换的隧道大变形组合预测方法

张 碧

(陕西铁路工程职业技术学院，陕西 渭南 714000)

基于小波变换的隧道大变形组合预测方法

张 碧

(陕西铁路工程职业技术学院，陕西 渭南 714000)

为提高隧道变形预测精度,首先，探讨不同小波变换参数的去噪效果，并将隧道的变形数据分为趋势项和误差项；之后，对趋势项和误差项进行单项预测和组合预测，对比分析本文预测结果，研究本文预测模型的有效性。结果表明：sym8小波函数在采用软阈值选取方法、启发式阈值标准及8层小波分解时的去噪结果最优。采用剔除最大误差倒数法通过对趋势项及误差项进行组合预测可知，趋势项组合预测、误差项组合预测较其单项预测的预测精度分别提高了2.5～3.5倍、4.0～5.4倍，达到了提高预测精度的目的，且也不同程度地提高了预测结果的稳定性。通过对本文预测模型的实例分析，验证了本文预测思路的可行性和有效性，预测结果满足大变形预测的要求，具有较高的可行度。

隧道工程；小波去噪；大变形；组合预测；剔除最大误差倒数法；对比分析

1 研究背景

在隧道施工过程中，围岩大变形是一种常见的施工灾害，对隧道的正常施工有较大影响和较大的安全隐患。因此，对隧道大变形的变形预测就显得格外重要，通过预测能有效掌握隧道的变形趋势，且可为大变形的临时处理措施提供一定的指导依据[1]。

在隧道的变形监测过程中，受隧道环境、仪器及人为等因素的影响，监测数据总是不同程度地含有一定的误差因素，而在以往的变形预测中往往没有考虑到误差因素对预测效果的影响。同时，在隧道误差因素的剔除过程中，小波变换具有良好的效果，如周大华等[2]利用小波去噪理论对一组隧道监测数据进行了去噪处理，得出小波分析能有效剔除监测数据中的噪声，并有效预测了隧道的发展趋势；胡纪元等[3]通过构建小波神经网络，克服了神经网络的缺陷，该预测模型具有结构简单且预测精度较高的特点。上述研究说明了小波去噪在隧道变形数据的处理过程中具有其适用性。

在隧道变形数据的预测方法中，已有许多学者在这方面进行了研究和分析，如刘开云等[4]采用遗传优化的支持向量机模型对一连拱隧道的变形进行预测，得出该模型的预测精度较高，可用于施工期的变形预测；赵朴[5]则采用变量轮换法优化支持向量机，实例验证了该模型的适用性和有效性；何亚伯等[6]利用GM(1，1)和时间序列模型对隧道的不同序列进行预测，结果表明该模型有效预测了隧道的变形发展趋势；林大炜等[7]利用BP神经网络模型对隧道的变形进行预测，结果表明该模型要优于传统的BP神经网络模型，具有一定适用性。

上述文献虽对隧道的变形预测进行了深入研究，但缺少对隧道变形的组合预测研究，也缺少对剔除最大误差倒数组合法的应用研究。因此，本文采用组合方法建立隧道大变形的预测模型，以期提高预测精度，增加预测结果稳定性。

2 组合预测模型基本原理

2.1 预测结构

本文旨在利用多种单一预测模型的预测数据，结合本文的组合思路，探讨本文隧道变形组合预测的效果，主要步骤为：

(1) 考虑到监测数据具有误差信息，探讨不同小波参数的去噪效果，分析不同参数在隧道变形去噪中的适用性和有效性，进而有效提取出隧道变形的趋势项。

(2) 采用GM(1，1)、支持向量机、BP神经网络和时间序列作为单一预测模型，对隧道的趋势项序列进行预测，并采用本文剔除最大误差倒数组合法对趋势项的预测结果进行组合预测。

(3) 采用支持向量机、BP神经网络和时间序列对误差序列进行预测，也采用本文剔除最大误差倒数组合法对误差序列的组合预测效果进行预测。

(4) 对比分析本文的预测结果，验证本文预测模型的可行性和有效性。

2.2 小波变换

小波变换已被许多实例验证其具有较好的去噪能力。在去噪过程中，由于原始数据产生的误差源具有差异，导致小波变换去噪过程中，相关参数的选取具有较大的影响，有必要对不同参数在隧道变形数据中的适用性进行探讨和研究，本文主要对如下参数的影响进行分析。

(1) 阈值选取方法。在小波变换的阈值选取过程中，常使用软阈值和硬阈值2种方法，且这2种阈值的选取方法具有一定的差异，去噪效果也与误差频率的分布有关。

(2) 阈值选取标准。小波变化的阈值选取标准包含了无偏估计、启发式阈值、固定式阈值及极大极小值阈值。不同阈值的去噪效果不同，有的去噪较彻底，但容易去掉真实信号；有的去噪较保守，易保留误差信号，因此有必要探讨合适的阈值标准。

(3) 小波分解层数。不同的分解层数能实现原始信号的综合分解，分解层数太少，易造成误差信号不能有效地被分解出去；分解层数太多，则不易将误差信号剔除，因此对小波分解层数应进行探讨。

(4) 小波去噪函数。不同的小波函数具有不同的去噪形式，且小波函数的阶数n对时域的支撑性和频带的划分效果具有较大的影响，因此，也应对其影响效果进行探讨。

同时，在小波变换的效果评价中，常用的评价指标有均方根误差(RMSE)、信噪比(SNR)、平滑度指标(r)等，且具有基于上述单一指标基础的组合指标，文献[8]中采用了组间组内修正的归一化综合指标H，本文沿用其指标形式，将其作为本文去噪效果的评价指标，表达形式为

(1)

式中：ε(R)，ζ(R)分别为均方根误差指标的组内权重和组间权重；ε(r)，ζ(r)分别为平滑度指标的组内权重和组间权重；ε(S)，ζ(S)分别为信噪比指标的组内权重和组间权重；PRMSE，Pr，PSNR分别为均方根误差、平滑度、信噪比指标的归一化值。

2.3 预测模型

本文在预测过程中，采用了GM(1，1)、支持向量机、BP神经网络和时间序列作为本文的基础预测模型，考虑到上述模型已被广泛的应用，且具有较好的适用性，限于文章篇幅，本文对各单一预测模型的基本原理不再赘述，主要将本文的预测思路进行介绍。

本文的组合预测是利用剔除最大误差倒数法，该方法是在误差倒数法基础上的改进和创新，主要是考虑到不同基础预测模型在不同节点的预测误差具有一定的差异，而最大误差在不同预测模型中也随节点呈动态变化的特点。因此，对比同一预测时刻不同预测模型的预测误差，并剔除其最大误差值，将其余的预测值按照误差倒数法确定权重值，且考虑到不同节点的误差有正负差异，所以在权值求解过程中是利用误差的平方值求解权重值。本文组合模型可表示为

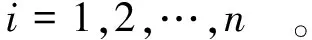
(2)

式中：L′(k)为组合预测值；li(k)为第i单项预测值；wi(k)为第i单项组合权值。

同时，基于GM(1，1)模型对系统机理的考虑不够，在误差序列的预测过程中，该模型预测精度较低。因此，在误差序列的预测过程中，不采用灰色模型的预测结果。

另外，为对比不同去噪效果及不同预测模型结果之间的差异，本文借鉴文献[8]中的期望和方差指标来作为本文结果评价的指标。其中，期望可用于对评价指标的精度进行有效的评价，而方差则可以实现对评价指标的稳定性评价。

3 实例分析

3.1 工程概况

为分析本文预测模型的可行性和有效性，以文献[9]为工程实例分析的数据来源。由文献[9]可知，某隧道为双线隧道，左右两线相距约30 m，左线长11 563 m，右线长11 595 m。隧道的围岩级别为Ⅳ，Ⅴ级，约占全线总长的60%。且通过对隧道区的应力测试，并结合《工程岩体分级标准》，该隧址区为极高应力区，具有产生大变形的条件。通过隧道施工过程中的监测，得出右线出现了大变形，并以YDK79+117的水平收敛变形数据作为本文分析的数据，变形如图1所示。

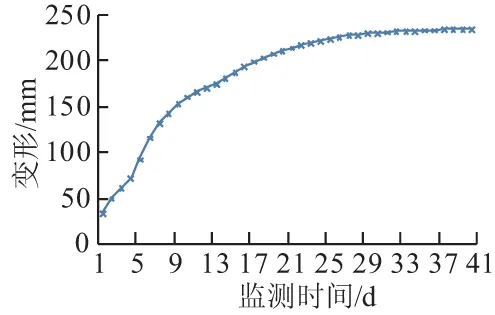
图1 隧道水平收敛累计变形Fig.1 Cumulative horizontal convergence deformation of tunnel

由图1可知，隧道水平收敛值最大达235.17 mm，变形量较大，促使隧道围岩内部裂隙的贯通和发育，破坏了围岩的完整性，降低了围岩的自稳能力。因此，对隧道的变形预测能有效地掌握隧道的变形趋势，为大变形的临时处理措施提供一定的依据。

3.2 小波变换分析

由于监测过程中的仪器、环境及人为因素等均很大程度上使得隧道的变形数据具有误差因素，而预测模型难以对含有误差因素的数据进行高效的预测。因此，本文采用小波变换对隧道的水平收敛数据进行处理，旨在求解出隧道的变形趋势项，实现对变形数据的分解组合预测。

3.2.1 阈值选取方法研究

由文献[8]的研究可得出，在小波变换中，小波变换参数对去噪效果有较大的影响，因此本文结合小波参数的特点，采用试算法确定最优的小波变换参数，得到最优的去噪数据。结合相关文献，将小波的分解层数确定为10层，采用启发式阈值来探讨硬阈值和软阈值2种阈值选取方法的效果，如表1所示。

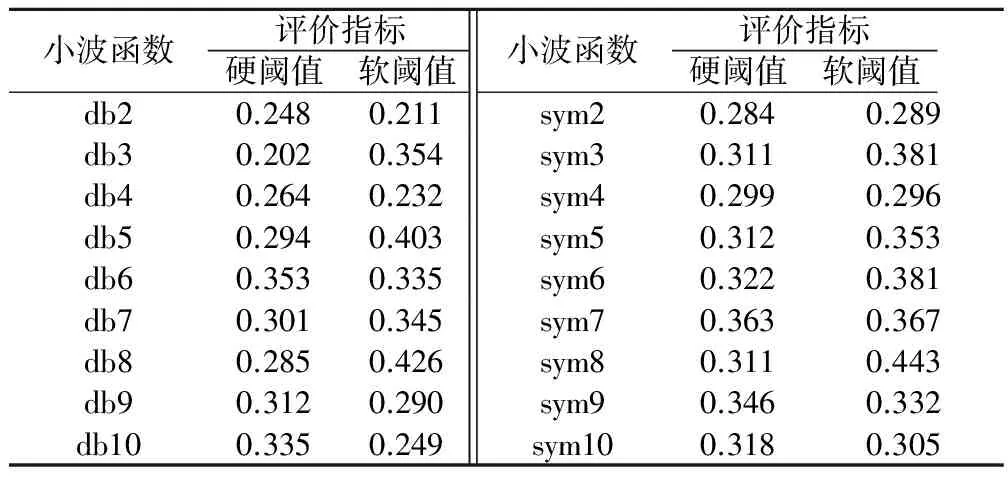
表1 阈值选取方法效果

注：评价指标由式(1)求得，是RMSE,SNR,r归一化值的综合值

由表1可知，小波函数及阈值的选取标准对去噪效果均具有较大的影响，在db小波系中，评价指标的最小值是db3小波函数采用硬阈值的评价值，为0.202，最大值是db8小波函数采用软阈值的评价值，为0.426；在sym小波系中，评价指标的最小值是sym2采用硬阈值的评价值，为0.284，最大值是sym8采用软阈值的评价值，为0.443。为进一步分析阈值选取方法等因素对去噪效果的影响，本文在采用期望和方差指标对其进行评价，结果如表2所示。

由表2可知，在db小波系和sym小波系中，软阈值的去噪效果均比硬阈值好，但硬阈值具有更好的稳定性，这与软阈值曲线的平滑性有关，但也增加了去噪效果的不确定因素，减弱了其稳定性；同时，sym小波系的去噪效果要优于db小波系的去噪效果。综上所述，本文确定软阈值作为本文的阈值选取方法。

表2 阈值选取方法的期望与方差

3.2.2 阈值选取标准研究

不同标准的去噪效果具有一定的差异。为探讨其各自的适用性，本文对阈值的选取标准进行分析，得到不同阈值选取标准的去噪效果也具有一定的差异。采用期望和方差评价不同阈值标准的去噪效果，结果如表3所示。

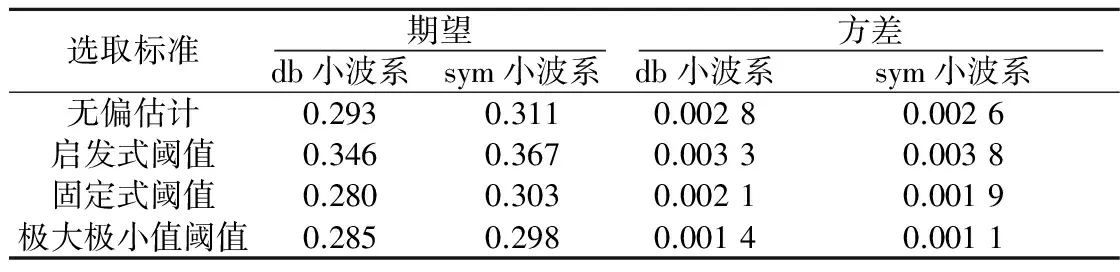
表3 阈值选取标准的期望与方差

由表3可知，不同阈值标准的结果之间，均以sym小波系的去噪效果最好，且以启发式阈值标准的去噪效果最好；同时，各阈值标准的方差值差异不大，规律性不强。综上所述，本文选取启发式阈值作为本文小波变换的阈值取值标准。

3.2.3 小波分解层数分析研究

小波分解层数对小波变换的影响较大。结合相关文献的研究成果，进一步对小波分解层数进行研究，计算结果如表4所示。

由表4可知，不同分解层数对小波变换的去噪效果也具有一定的差异。对比2种小波系在对应分解层数的去噪结果可知，sym小波系的结果要优于db小波系的结果，这与前文分析基本相符，进一步验证了本文的研究成果。在sym小波系的分解结果中，根据期望统计指标，得出10层和12层分解的结果差异不大，且以12层分解的结果最优。因此，选取12层作为本文小波变换的分解层数，并对小波阶数的相关指标进行统计，如表5所示。

由表5可知，在同一阶数时，sym小波函数的去噪效果也是要优于db小波系。在db小波系中，阶数较大的去噪效果要略优于阶数较小的去噪结果，而在sym小波系中，阶数对去噪效果的影响不明显，结果之间相差变化不大。

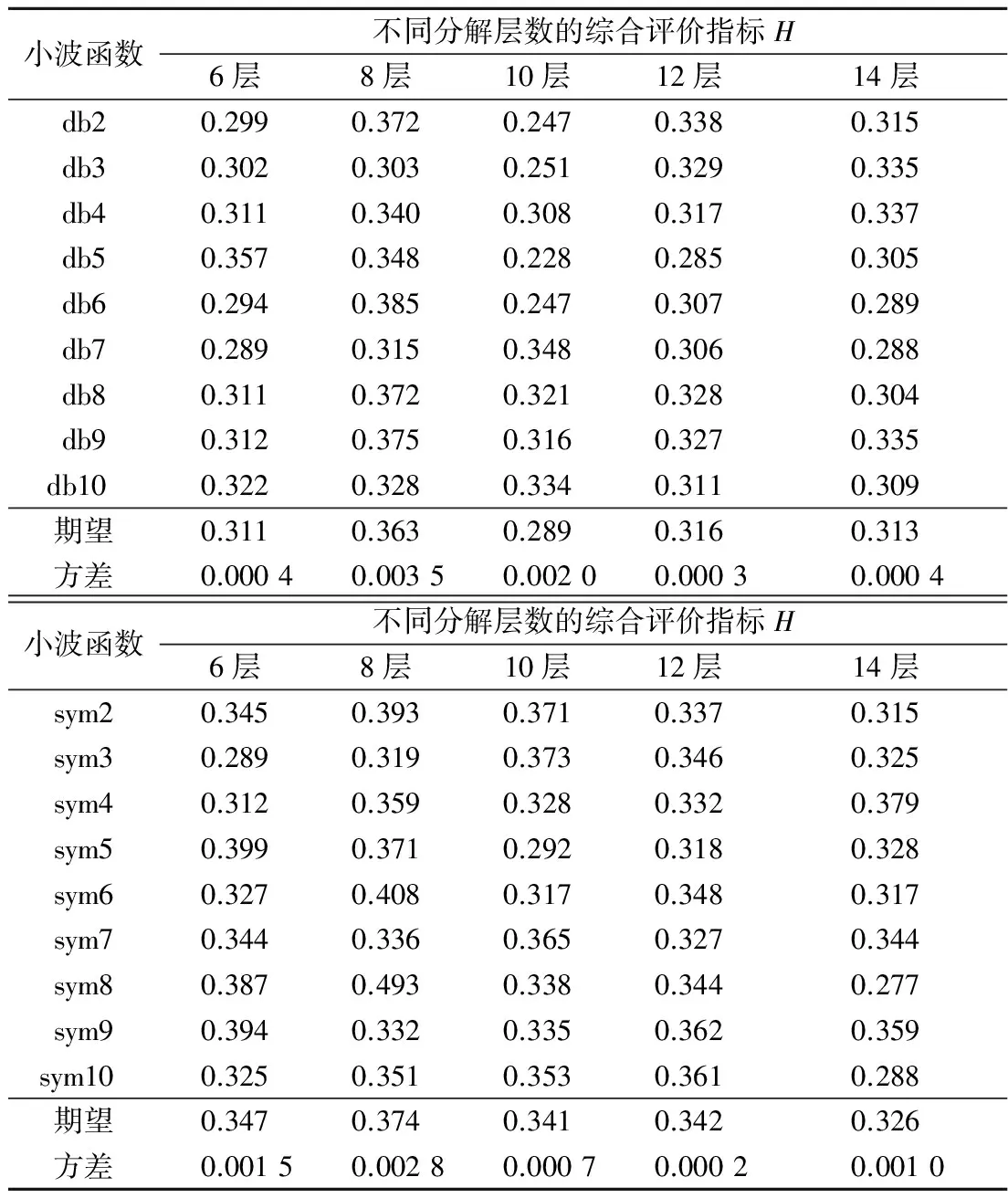
表4 小波分解层数效果

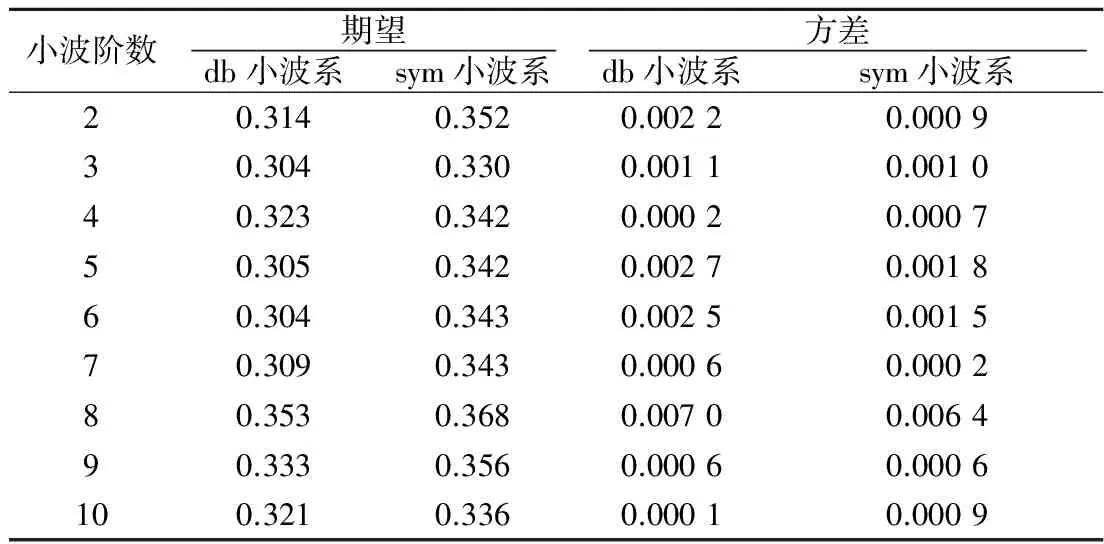
表5 小波阶数的影响结果分析

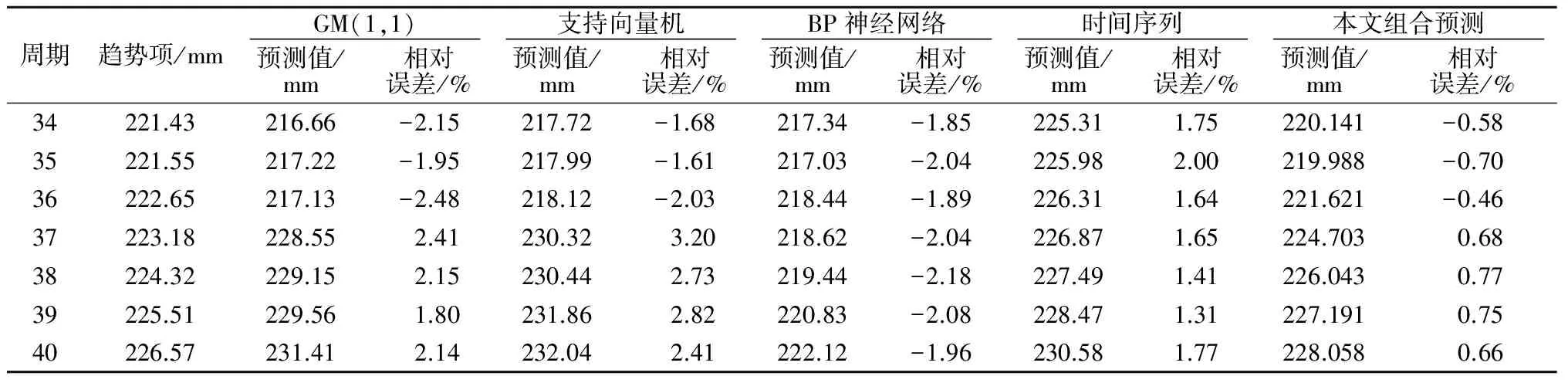
表6 趋势项组合预测成果

注：相对误差=(预测值-趋势项)/趋势项×100%

同时，对比2种小波函数在不同阶数的方差结果，得出不同阶数处的方差值相差不大，随阶数变化的规律性不强。综合上述研究，本文采用sym8小波函数在软阈值的选取方法，将启发式阈值的标准及8层小波分解的去噪结果作为本文趋势项与误差项的分离结果。

3.3 分项组合预测

3.3.1 趋势项组合预测

基于对隧道变形监测数据的小波变换，本文结合前文的预测结构安排，分别对趋势项及误差项进行分项组合预测。在趋势项的组合预测过程中，单项预测包含了GM(1，1)、支持向量机、BP神经网络和时间序列，组合预测方法采用本文创新性提出的剔除最大误差倒数法，预测结果如表6所示。

由表6中的预测结果可知，不同单项预测模型在不同节点处的预测结果具有一定的差异，这体现出了不同预测模型具有不同的适用性，而本文采用单节点的非线性组合，能很大程度上剔除了各模型在不同节点处的最大误差，也能很好地综合利用各模型的成果，提高预测结果的稳定性和精度，较单项预测的预测精度提高了2.5～3.5倍。

为有效对比各模型之间的预测效果，采用期望和方差对趋势项的预测结果进行统计分析，结果如表7所示。

表7 趋势项预测期望与方差

由表7可知，4种单项预测的结果具有一定的差异，验证了不同预测模型具有不同的适用性和有效性，并通过组合预测，有效提高了预测精度及稳定性，验证了本文预测模型及思路的有效性。

3.3.2 误差项组合预测

采用支持向量机、BP神经网络和时间序列对误差项进行了进一步的修正预测，并采用同样的组合预测模型，对其进行组合预测，预测结果如表8所示。

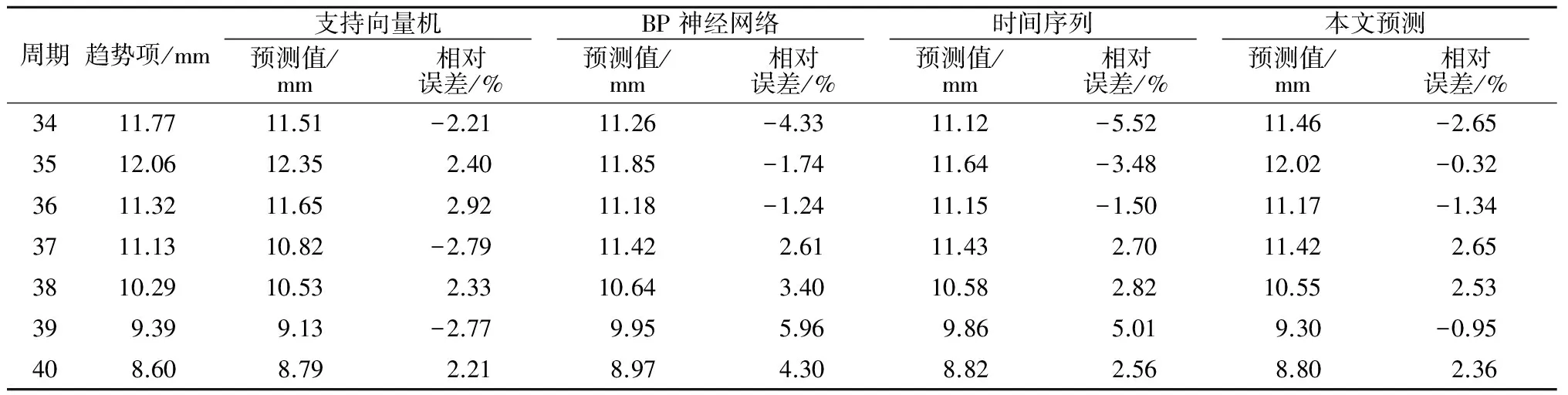
表8 误差项组合预测成果

由表8可知，在相应各预测节点处，多以本文预测结果的预测精度更高，再次验证了组合预测模型能有效提高预测精度，具有较好的适用性和推广性。

同时，进一步采用期望和方差指标来评价预测效果，结果如表9所示。由表9得出本文的组合预测模型很大程度上提高了预测精度，验证了本文预测模型的有效性。但是对比不同预测结果的方差值，得出本文的组合预测模型并不是所有模型中最优的。这说明在误差项的组合预测过程中，预测精度得到了提高，但对预测结果的稳定性提高较小。

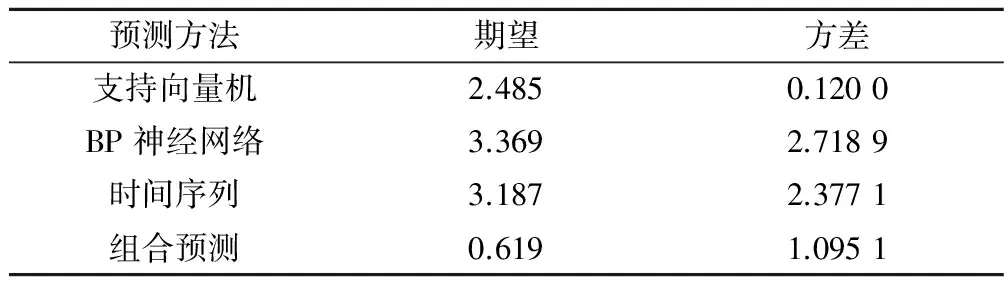
表9 误差项预测期望与方差

3.3.3 组合预测结果

通过对趋势项及误差项的组合预测，将两者结果进行叠加，得到本文隧道水平收敛变形的预测值。为验证本文预测模型的有效性，将其与文献[9]中的预测结果进行对比分析，结果如表10所示。通过对比文献[9]及本文的预测结果，得出本文的预测精度要优于文献[9]的预测精度，验证了组合预测模型的有效性。

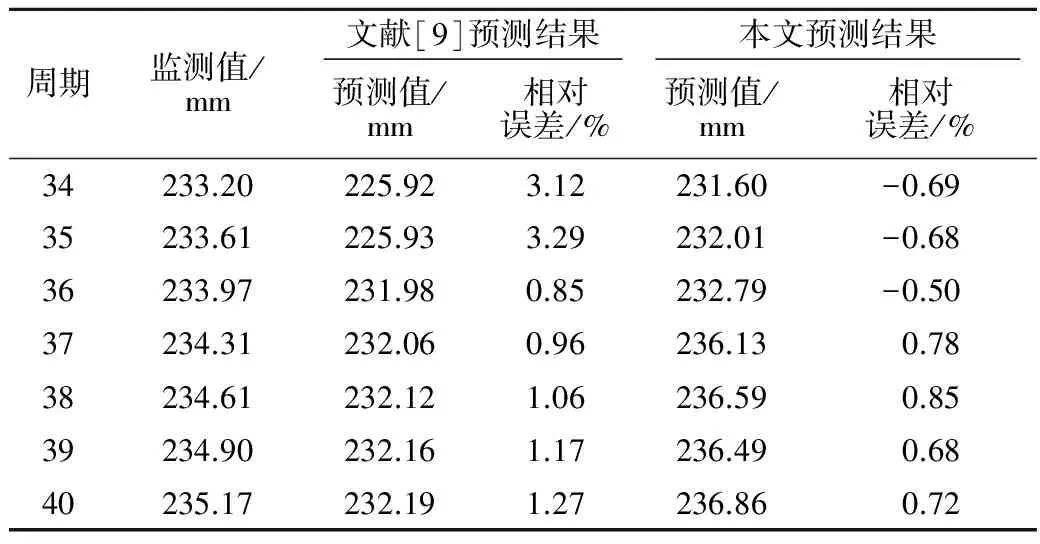
表10 预测结果对比

注：相对误差=(预测值-监测值)/监测值×100%

4 结 论

(1) 通过对小波变换对隧道变形数据的去噪分析，得出软阈值选取方法、启发式预测标准及sym小波系函数的去噪效果较好，能有效去除变形数据中的误差信息。

(2) 通过对趋势项及误差项的组合预测，得出本文的组合预测模型较单项预测模型的精度要高，说明了本文组合预测模型的有效性。

(3) 通过对比本文与相关文献的预测结果，得出本文的预测模型进一步地提高了预测精度，为隧道的变形预测提供了一种新的思路和方法。

[1] 王开洋，尚彦军，何万通，等. 深埋公路隧道围岩大变形预测研究[J]. 地下空间与工程学报，2015，11(5):1164-1174.

[2] 周大华，肜增湘，陈建平. 基于小波分析的隧道监测数据处理[J]. 现代隧道技术，2010，47(4):58-61.

[3] 胡纪元，文鸿雁，周 吕，等. 基于小波神经网络的隧道变形预测模型研究[J]. 公路工程，2014，(4):26-29.

[4] 刘开云，乔春生，刘保国. 高速公路连拱隧道施工变形预测的GA-SVR智能模型研究[J]. 公路交通科技，2009，26(5):75-79.

[5] 赵 朴. 基于变量轮换法的支持向量机在隧道围岩变形预测中的应用[J]. 石家庄铁道学院学报(自然科学版)，2009，22(3)：61-64.

[6] 何亚伯，梁 城. 非等距时间序列模型在隧道拱顶位移预测中的应用[J]. 岩石力学与工程学报，2014，33(增2):4096-4101.

[7] 林大炜，林从谋，黄逸群，等. 小净距2扩4隧道变形规律的BP小波神经预测[J]. 华侨大学学报(自然科学版)，2014，35(2):207-211.

[8] 杨哲峰，罗 林，贾东彦，等. 基于小波去噪的深基坑变形预测研究[J]. 人民长江，2014，45(19):41-46.

[9] 王树栋，刘开云. 长大隧道软弱围岩施工大变形智能预测方法[J]. 中国铁道科学，2008，29(2):82-87.

(编辑：黄 玲)

Combinatorial Forecasting Method for Large Deformationof Tunnel Based on Wavelet Transform

ZHANG Bi

(Shaanxi Railway Institute，Weinan 714000，China)

In order to improve the accuracy of tunnel deformation prediction, firstly，we discussed the denoising results by different wavelet transformation parameters，and divided the tunnel deformation data into trend term and error term. Secondly，we established individual and combinatorial forecasting models to predict the trend term and error term, and compared the results so as to verify the proposed prediction model in this paper. The results show that the denoising results of Sym8 wavelet function are the optimum by using the soft threshold selection method，heuristic threshold criteria and eight-layer wavelet decomposition. By removing the maximum error and then determine the weights of the rest predicted values in reciprocal order, the prediction accuracy of trend term and error term by combinatorial forecasting model has improved by 2.5-3.5 times and 4.0-5.4 times respectively than that by individual forecasting model, hence the reliability of the prediction results are enhanced. Through example analysis of the prediction model，we verified the feasibility and validity of this prediction method，and the results of high feasibility could meet the requirements of large deformation prediction.

tunneling engineering; wavelet denoising; large deformation；combination forecasting; error reciprocal after removing maximum error; comparative analysis

2016-05-05；

2016-08-26

张 碧(1979-)，男,山西沁县人，副教授，硕士，主要从事道路与铁道工程专业的教学与研究工作，(电话)13892590855(电子信箱)82250997@qq.com。

10.11988/ckyyb.20160404

2017,34(7):94-98,105

U451.2

A

1001-5485(2017)07-0094-05