斜坡上的密度流数值模拟研究

米博宇，张小峰，任 实

(1.武汉大学 水资源与水电工程科学国家重点实验室，武汉 430072; 2.中国长江三峡集团公司，湖北 宜昌 443133)

斜坡上的密度流数值模拟研究

米博宇1，张小峰1，任 实2

(1.武汉大学 水资源与水电工程科学国家重点实验室，武汉 430072; 2.中国长江三峡集团公司，湖北 宜昌 443133)

为了探讨均匀密度环境水体中斜坡密度流的运动规律，建立了立面二维RNGk-ε紊流数学模型，通过与已有试验资料对比，验证了该模型的合理性与准确性。利用该模型模拟不同坡角和流量下的斜坡密度流，研究结果表明:密度流头部流速与坡角具有一定的函数关系，存在一个最优坡角使得相同条件下的头部流速最大；头部流速与浮力通量的三次方根之间并非严格的正比例函数关系，在流量较小或较大时将发生偏离；密度流运动过程中，头部形态不断扩大，头部的厚长比逐渐减小；头部扩大的速率随着坡角和流量的增大而增大，最后逐渐趋于一个稳定速率。研究结果能够帮助进一步了解斜坡密度流的运动规律。

密度流；斜坡；头部流速；数值模拟；RNGk-ε紊流模型

1 研究背景

本文将在前人研究成果的基础之上，采用数值模拟的方法，与已有试验资料进行对比分析，进一步探讨均匀密度环境水体中斜坡密度流的运动规律，重点分析斜坡坡角与进口流量对密度流头部流速与形态的影响。

2 数学模型与验证

Choi等[5]采用标准k-ε紊流模型模拟斜坡上的密度流，验证了其可行性，本文在此基础上改用RNGk-ε紊流模型，根据Patankar[6]求解流场的思想，将方程组中各方程以统一形式表达为

(1)

控制方程包括Reynolds平均Navier-Stokes方程(简称RANS)和RNGk-ε紊流模型方程(具体参考文献[7])。计算方法采用Patankar提出的SIMPLER算法。压力采用SIMPLER算法中的压力方程直接求解，与传统的采用Boussinesq假设将密度的变化转换成浮力项这一做法相比，本文的数学模型直接将压力差所导致的浮力还原到压力场中，因为获取压力场时并没有采用常密度假设，而是根据实时的密度场与速度场求解得来。

边界条件参考陶文铨[7]在其著作中给出的边界提法，其中压力与压力修正方程在各类边界上采用二类边界条件，动量方程与k-ε方程在边壁上采用壁面函数法，k-ε模型方程中的参数取值与文献[7]中的推荐取值一致。

采用典型算例对数学模型进行验证，算例取自双层密度流体中的侵入密度流试验，这类问题已经被Britter等[8]、Lowe等[9]多位学者广泛研究过，并取得了基本一致的结论。算例设置如图1(a)所示，竖直平面内有一长(x方向)1.0 m、高度(y方向)>0.2 m的矩形水槽，3种不同密度的水体分别位于A，B，C 3个区域，其中ρA=(ρB+ρC)/2，ρB<ρC，A区域与B，C区域之间有一块挡板隔离，初始处于静止状态。水槽顶部为空气边界，四周及底部为固壁边界。突然撤去中间的挡板，由于ρB<ρA<ρC，重力作用下，A与B，C的交界面上会产生压强差，驱使原来静止的流体开始流动，从而形成侵入密度流，如图1(b)所示。

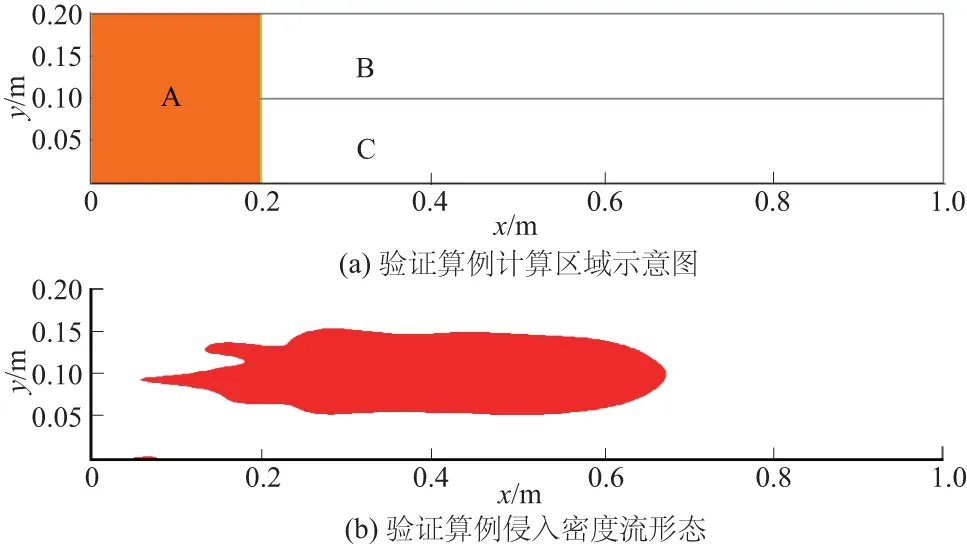
图1 验证算例计算区域与侵入密度流形态Fig.1 Calculation areas and intrusive density current shape of verification example

表1 本文数值模拟结果与Lowe等[9]试验结果对比

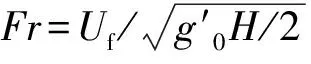
图2 斜坡计算区域示意图Fig.2 Schematic diagram of calculation area of slope

3 计算工况

对于斜坡上的密度流，本文的计算区域如图2所示，斜坡顶端有一入口，高密度水体从此处流入环境水体中，斜坡角度为θ，竖直高度为H2，斜坡顶端距水面高度为H1，整个计算区长度根据θ的不同而略有变化。所有计算工况中，进口高度均为1 cm，为了尽量减小水面对密度流的影响，取H1=15 cm，H2=15 cm，坡角θ范围为5°～40°，环境水体密度ρa=1 000 kg/m3，入流水体密度ρi=1 015 kg/m3。

为了分析坡角和流量对密度流的影响，本文的计算工况分为2大类(工况编号以“I-”和“II-”标志)。第1类工况共13个，进口流量(单宽)统一为3×10-4m3/(m·s)，坡角标在工况编号中，如“I-5”表示第1类中坡角为5°的工况，以此类推；第2类工况共11个，坡角统一为10°，进口流量标在工况编号中，如“II-3”表示第2类中进口流量为3×10-4m3/(m·s)的工况，以此类推。

4 模拟结果

斜坡上每个工况中的密度流都有一个明显的头部，后面紧跟较薄的尾部，部分坡角下的密度流在同一时刻的形态如图3所示。

图3 密度流形态Fig.3 Shape of density current

从图3中可以看出，头部最前端都有一定的抬升，都是离开边壁的，坡角越大，在同一时刻形成的密度流头部也越大，尾部形态则没有明显区别。这与Britter等[1]的试验现象相吻合。

取各个工况中密度流头部的位置和形态与时间的对应关系进行分析，可以发现密度流在沿斜坡向下运动的过程中头部的速度Uf经过一定的调整后保持恒定，头部大小(包括长度L和厚度h)则因卷吸作用不断增大，且与时间近似呈线性关系。具体数值列于表2中，其中Uf是恒定以后的头部速度，αL是L随时间的增长率，αh是h随时间的增长率，头部雷诺数Re=(g′0q)1/3h/ν，g′0=2g(ρi-ρa)/(ρi+ρa)为入流的相对重力加速度。由于头部厚度h是不断变化的，本文选取分析时段内的最小Re作为代表值，即表2中的Remin。带星号(*)的2个工况中，L和h与时间t的关系更接近于一条曲线，而非其他工况中的线性关系，说明增长率αL和αh未能稳定，因此其相应结果不参与本文数据分析，但头部位置与时间的关系明确，且与其他工况规律一致，故将其Uf值纳入分析范围。

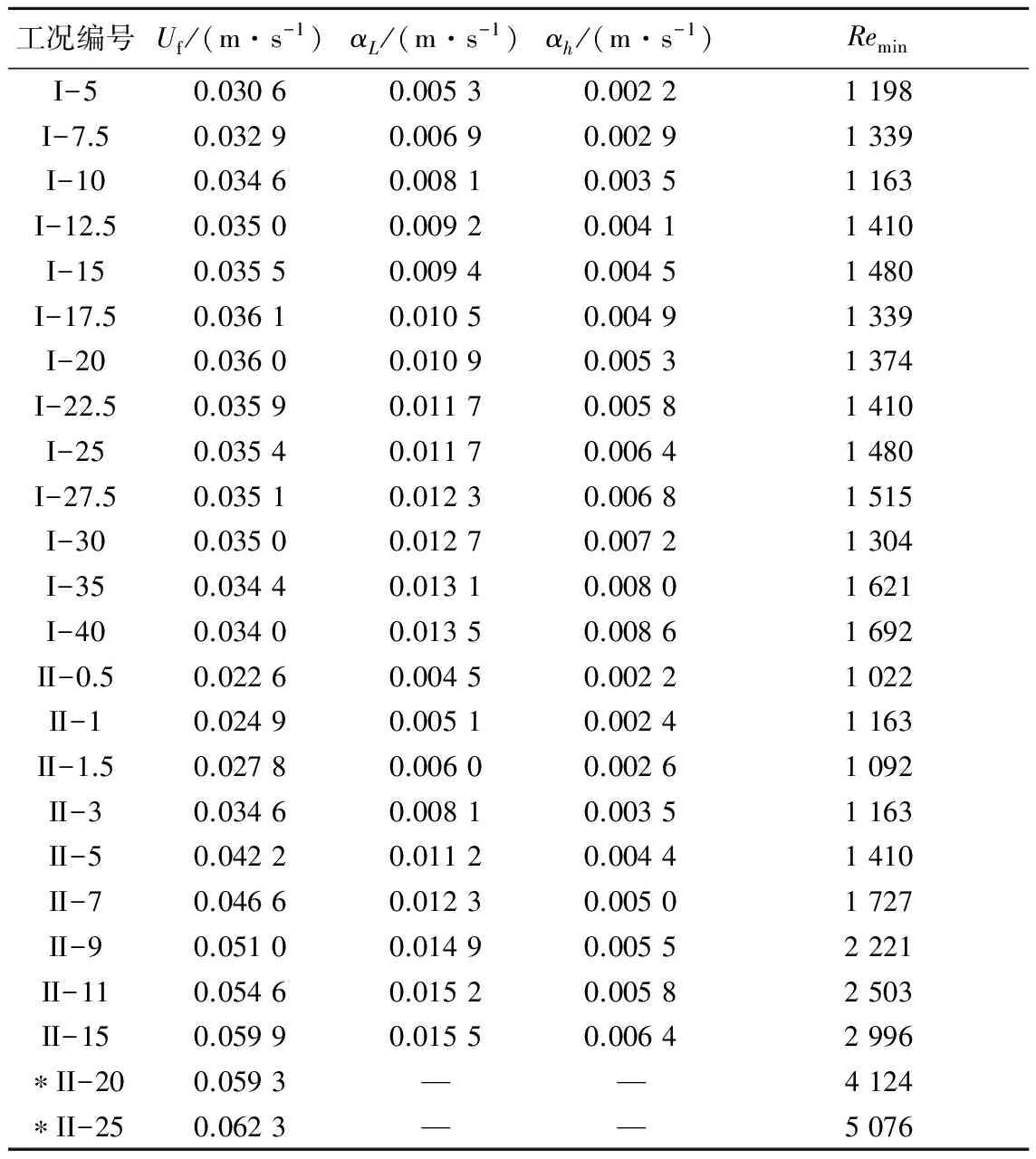
表2 各工况特性

4.1 头部流速的规律

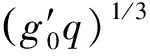
图4 头部流速与坡角的关系Fig.4 Relations of head velocity vs. slope gradient and

密度流自进口流入环境水体以后，初始流速发展到最后的恒定流速，会经历一个调整阶段。本文第1类工况的进口流速均为0.03 m/s，从图4(a)可以看出，所有工况中的密度流头部都会经历一个加速过程到它的恒定流速，这一过程历时为5～12 s不等，且历时长短与图4(a)曲线走势大致吻合。同样在第2类工况中也有类似情况。调整完成以后进入稳定阶段，头部流速不再变化。

影响密度流头部流速的主要力学因素有密度流在环境水体中的净重力G、斜坡上的阻力fs与支持力N、以及环境水体的阻力fa，这些力之间的平衡决定了头部流速的恒定。在沿斜坡方向，G的分力是密度流流动的驱动力，流动过程中形成的阻力fs和fa是与流速呈正相关的。当初始流速过小时，驱动力大于阻力，密度流会加速流动，反之则会减速，直到某一流速恰好使得阻力等于驱动力以后，密度流处于受力平衡状态，流速不再变化。同样条件下，坡角越大，驱动力也越大，达到平衡时需要的流速也越大。但fa不仅与流速有关，还与密度流头部的形态有关，头部越大，受到环境水体的阻力自然越大。从图3可以看出，同一时刻，坡角越大，密度流头部也越大，由此带来的阻力减小了对于流速所引起的阻力的需求，因而密度流头部流速并不是随着坡角增大而一直增大的。Britter等[1]的试验数据与本文的数值结果都显示在坡角为20°左右时，密度流流速最大，至于这一最优坡角的具体值以及跟其他因素间的关系还有待进一步研究。

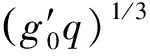
图5 Uf与(工况II-3至II-11)，q的关系Fig.5 Relations of Uf vs.(in conditions from II-3 to II-11) and q

密度流头部流速与驱动力大小密切相关，当坡角一定时，驱动力大小取决于头部的相对重力加速度g′0h，而g′0h由头部与环境水体密度决定。取同一时刻各个流量下的密度流头部中心位置的密度分布(见图6)进行分析，分布曲线从内到外流量依次增加。

图6 同一时刻各个流量下头部密度分布Fig.6 Distribution of head density under various flow rates at the same time

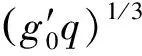
4.2 头部形态的规律

密度流头部在沿斜坡向下运动的过程中，由于尾部高密度水体的汇入，以及与环境水体间的掺混作用，头部是不断增大的[1]。以头部厚度h与长度L作为参考指标，本文数值模拟的结果显示h和L与时间t有着较好的线性关系。从表2可以看出，h和L随时间的增长率有明显的差别，L增长的速率要快于h，说明密度流头部在运动过程中是不断扁平化发展的。各工况的计算结果表明，随着坡角的增大，同一时刻形成的密度流头部的厚长比h/L是逐渐增大的，在θ=40°工况中最大能到0.72，图3也直观地反映了这一现象。随着密度流头部的运动， h/L是逐渐减小，在θ=5°工况中最小能到0.44。这些现象均与试验观测相符。分析h和L的增长率与坡角和流量的关系，如图7所示。

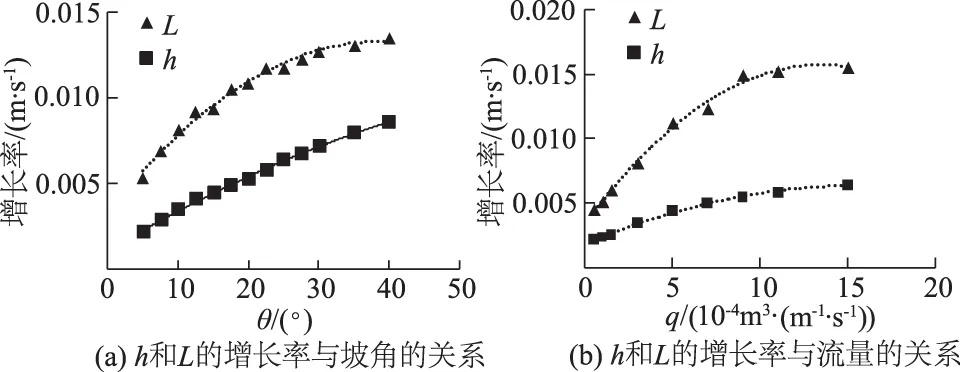
图7 h和L的增长率与坡角、流量的关系Fig.7 Relations of growth rates of h and L vs. slope gradient and discharge

从图7中可以看出，随着坡角或流量的增大，h和L增长率逐渐趋于一个稳定水平，并非线性增长。

5 结 论

(1) RNGk-ε紊流模型可以准确地模拟密度流的流动，对于头部流速等参数的模拟结果与试验观测一致，因此可以用来进行密度流的相关研究。

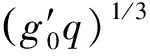
(3) 坡角对密度流头部流速的影响较小，数值模拟的结果与试验数据均表明存在一个最优坡角使得相同条件下密度流的头部流速最大。造成这一现象的原因是坡角的变化在改变密度流驱动力的同时也改变了头部的形态，使得阻力也发生了变化，二者的相互制约形成了头部流速与坡角间的关系。

(4) 密度流在运动过程中头部形态不断扩大，坡角越大，流量越大，扩大的速率越快，但这一速率并不是随坡角或流量线性增长的，而是逐渐趋于一个稳定值。头部在扩大的同时，形状也在发生改变，随着时间推移，头部越来越扁平。

[1]BRITTERRE,LINDENPF.TheMotionoftheFrontofaGravityCurrentTravellingdownanIncline[J].JournalofFluidMechanics, 1980, 99(3): 531-543.

[2]ALAVIANV.BehaviorofDensityCurrentsonanIncline[J].JournalofHydraulicEngineering, 1986, 112(1): 27-42.

[3]BAINESPG.MixinginFlowsdownGentleSlopesintoStratifiedEnvironments[J].JournalofFluidMechanics, 2001, 443: 237-270.

[4]CENEDESEC,ADDUCEC.MixinginaDensity-drivenCurrentFlowingdownaSlopeinaRotatingFluid[J].JournalofFluidMechanics, 2008, 604: 369-388.

[5]CHOISU,GARCíAMH. k-εTurbulenceModelingofDensityCurrentsDevelopingTwoDimensionallyonaSlope[J].JournalofHydraulicEngineering, 2002, 128(1): 55-63.

[6]PATANKARSV.NumericalHeatTransferandFluidFlow[M].USA:HemispherePublishingCorporation, 1980: 1-154.

[7] 陶文铨. 数值传热学(第2版) [M]. 西安: 西安交通大学出版社, 2001: 347-360.

[8]BRITTERRE,SIMPSONJE.ANoteontheStructureoftheHeadofanIntrusiveGravityCurrent[J].JournalofFluidMechanics, 1981, 112: 459-466.

[9]LOWERJ,LINDENPF,ROTTMANJW.ALaboratoryStudyoftheVelocityStructureinanIntrusiveGravityCurrent[J].JournalofFluidMechanics, 2002, 456: 33-48.

[10]BENJAMINTB.GravityCurrentsandRelatedPhenomena[J].JournalofFluidMechanics, 1968, 31(2): 209-248.

(编辑：罗 娟)

Numerical Simulation of Density Current on a Slope

MI Bo-yu1, ZHANG Xiao-feng1, REN Shi2

(1.State Key Laboratory of Water Resources and Hydropower Engineering Science, Wuhan University, Wuhan 430072, China；2.China Three Gorges Corporation, Yichang 443133，China)

A vertical two-dimensional RNGk-εturbulent model is established and its reasonability and accuracy are verified by comparison with existing experimental data. Density current on a slope in the presence of different slope gradients and discharges is simulated, and results reveal that 1) the head velocity of density current has a function relationship with the slope gradients, and there is an optimal slope gradients which maximizes the head velocity under the same condition; 2)the relation between head velocity and the cubic root of buoyance flux is not a strict proportional function, deviating under small or large discharge; 3)the head shape is enlarged in the motion process of density current, and the ratio of thickness to length of the head decreases gradually; 4)the growth rate of the head increases with the increase of slope gradients and discharges, and finally tends to a steady rate. These results could help further understand the motion pattern of density current on slope.

density current; slope; head velocity; numerical simulation; RNGk-εturbulent model

2016-04-12；

2016-06-03

米博宇(1992-)，男，湖北安陆人，硕士研究生，主要从事水力学数值模拟方面的研究，(电话)15527820486(电子信箱)miboyu@whu.edu.cn。

10.11988/ckyyb.20160346

2017,34(7):60-64

TV133.2

A

1001-5485(2017)07-0060-05