山区河流卵石河床的推移质输沙特性

蔡炳云

(上海勘测设计研究院有限公司 四川分公司，成都 610000)

山区河流卵石河床的推移质输沙特性

蔡炳云

(上海勘测设计研究院有限公司 四川分公司，成都 610000)

宽级配卵石河床表层大多为不同粗化程度的粗化层覆盖，现有大多数公式只能反映特定粗化程度下的输沙特性，限制了这些公式的适用性。理论分析和试验结果表明:在同样的来水来沙条件下，粗化程度越高，输沙率越小，在计算中引入粗化程度参数可以较好地提升公式的适用性;粗化层的稳定性对卵石推移质输沙有重要影响，粗化层遭受破坏后，推移质输沙率剧增，现有公式计算结果明显偏小。因此，在计算推移质输沙率时需要科学合理地考虑粗化层破坏导致的输沙率剧增问题。

卵石河床；推移质输沙率；粗化程度；粗化层稳定性；临界条件

1 研究背景

推移质输移是河流动力学的基本问题之一。理论上，它是研究推移质泥沙运动和河床冲淤规律的基础；实践上，它又是解决河床演变计算、水库淤积、水力输送固体物质、物理模型试验加沙率和有关数学模拟计算等问题不可缺少的工具。因此，研究和探求推移质输沙规律历来是一个十分重要的课题。

早在19世纪末期，法国的Duboys[1]第一次提出推移质运动的拖曳力理论，并建立推移质输沙率公式。自此以后，从事这方面研究的人员非常之多，国内外学者从不同的角度、以不同的水力泥沙因子为基础提出了不同的理论，从不同的角度提出了各自的输沙率公式。国外在推移质输沙方面的研究主要有以下几种类型：Meyer-Peter公式[2]以大量试验工作为基础，在欧洲运用较为广泛；Bagnold公式[3]是根据普通物理学的基本概念获得的；Einstein[4]则采用概率论与力学相结合的办法建立起来推移质输沙公式；Parker等[5]、Wilcock[6]则建立了基于床面表层泥沙的推移质输沙公式。国内关于推移质输沙方面的研究也有很多：韩其为[7]建立了基于泥沙运动统计理论的推移质输沙公式；秦荣昱等[8]提出了区分泥沙受荫蔽或暴露作用的临界粒径概念，建立了推移质输沙公式；孙志林等[9]基于统计理论建立了非均匀沙分组输沙公式；刘兴年等[10]考虑了河床粗化对推移质输沙率的影响；还有其他一些学者如钱宁[11]、曹叔尤等[12]也对推移质输沙研究做出了贡献。上述学者从不同的角度对推移质输沙进行研究，这也从侧面反映了推移质输沙的复杂性。

山区河流河谷狭窄弯曲，两岸地质构造发育，岩石风化破碎，构成河床的床沙多为砾石、卵石挟沙物质，颗粒粗，级配分布宽，河床的表层也大多为粗化层覆盖，在研究卵石河床的推移质输沙特性时，不得不考虑床面粗化程度对推移质运动的影响，更增加了问题的复杂性，使得卵石河流的推移质输沙问题更难解决。现有的各家推移质输沙公式虽然一般都通过了理论分析和试验验证，但一般只能反映某一特性河流的推移质输沙特性，公式的通用性较差。Gomez等[13]用实测资料对一些推移质输沙公式的适用性进行了比较分析，发现“没有一个公式能一贯表现良好”；Van Der Scheer等[14]运用实测资料对国外很多公式进行了测试，发现“很多公式性能不良”；Reid等[15]分析了6条卵石河流的推移质输沙情况，认为“各条河流的推移质输沙特性相差很大，建立通用的推移质输沙公式几乎是不可能的”。产生这种现象是因为卵石河床粗化对泥沙起动和推移质输沙能力影响较大，而各条河道的床沙粗化程度不尽相同，因而输沙能力相差也较大，即使同一河段的不同时期，河床粗化程度也不相同，输沙能力也就不同，这也是目前卵石起动输移、推移质输沙计算与实际情况相差较大的原因。本文分析了泥沙补给不充分条件下的卵石河床的推移质输沙特性，探讨了卵石河床的粗化程度对推移质输移的影响。

2 均匀卵石河床的推移质运动

在最初的推移质输沙研究中，试验研究是最主要的手段，试验用沙基本为均匀沙，研究成果为均匀沙的输移研究积累了丰富的资料。Meyer-Peter公式[2]的全部推导过程都是建立在大量试验基础上的，其资料的变化范围相当大，特别是包含了中值粒径达30 mm的卵石试验数据。Bagnold[3]认为推移质运动应像其他任何物理现象一样，应该遵循一些基本的运动规律，在此基础上建立了推移质输沙公式。Einstein[4]根据水槽试验长期观察的结果，注意到床面泥沙颗粒运动具有随机性，在推移质和床沙之间存在着不断的变化。其他的推移质研究大都以这3家公式的某些概念为基础。钱宁[11]最先对各家推移质公式进行了统一，根据钱宁的分析，均匀卵石推移质的输沙公式可统一表达为

(1)

式中：gb为推移质输沙率；τ为床面切应力；τc为床沙临界起动切应力。

老一辈学者在均匀推移质运动研究中所取得的成果，在实践中应用较为广泛，只要根据所需计算的水流和泥沙条件，选择合适的公式进行计算，一般均能给出较为满意的结果。

3 粗化过程中的宽级配卵石河床的推移质运动

3.1 山区河流卵石河床的粗化现象

山区河流构成河床的泥沙多为卵、砾石挟沙物质，颗粒粗，级配分布宽，河床表层大多为粗化层覆盖，床面表层泥沙颗粒远较次表层泥沙颗粒粗，见图1。

图1 The River Wharfe河床面粗化层照片及岷江谢家坝床沙粒径分布Fig.1 Photo of the armoring layer of the River Wharfe and particle size distribution of bed sand of Xiejiaba of Minjiang River

图1中，The River Wharfe河的泥沙补给严重不足，岷江河床表面大多为卵砾石所覆盖，其泥沙受补给程度也很低。由图1可见，卵石河床在一定的水流条件下，受泥沙分选的影响，床面大多处于不同的粗化状态，床面表层的泥沙颗粒远较次表层泥沙颗粒粒径大。

3.2 粗化作用对推移质输沙的影响分析

由图1可知，山区卵石河床的表层大多为宽级配泥沙所覆盖。宽级配非均匀沙的起动输移不仅与水流条件、床沙级配组成有关，而且与床沙位置、粗化程度有密切的关系。各条河流的水沙过程和床沙组成不同，致使其粗化状态也不尽相同，因此推移质输移亦具有相异的特性。

以水槽试验为例，把某一宽级配非均匀沙铺于水槽，释放流量为Q的清水(流速为U)，清水冲刷达至稳定粗化层形成，此为试验Ⅰ；停水，再释放同一流量Q，则水槽中床沙保持不动，此为试验Ⅱ；再停水，并测取粗化表层泥沙级配，按此级配铺于水槽中，并保持与前一试验稳定粗化层同一坡度，再释放流量Q，则床沙中部分颗粒将起动输移，此为试验Ⅲ。试验Ⅱ与试验Ⅲ的床面泥沙级配是相同的，坡降相同、流量相同也将保证水流强度是相同的，一般来说,试验Ⅱ与试验Ⅲ床面泥沙的输移情况应当相同。但试验现象表明，试验Ⅱ无泥沙起动，试验Ⅲ却有部分泥沙颗粒起动输移。试验Ⅱ与试验Ⅲ最大的不同在于：试验Ⅱ在水流的冲刷下，床面泥沙颗粒将进行位置调整，床面泥沙颗粒间形成了较为密实的结构，提高了试验Ⅱ末期床面的所有泥沙颗粒的抗冲性；试验Ⅲ的泥沙颗粒级配虽然与试验Ⅱ相同，但由于床面泥沙颗粒较为松散，抗冲性能弱于试验Ⅱ末期的粗化层床面，因此才会有泥沙颗粒起动输移。

Parker等[5]在对Oak Creek河进行调查研究时发现，在粗化程度较高时，床面表层细颗粒受到的荫蔽作用很大，其起动临界条件甚至与河床表层中值粒径泥沙颗粒相同。其实这种现象与试验Ⅱ、试验Ⅲ现象非常相近，在清水冲刷粗化试验末期粗化层形成后，虽然表层床沙仍然有不少较细颗粒，但基本不再起动输移。Hassan等[16]通过分析试验资料得出粗化床面的切应力中有17%～ 47%是由于床面结构引起的，其余则主要由颗粒本身引起，粗化保护层的形成，保护了相对细小的颗粒。Wittenberg等[17]在研究卵石河床泥沙输移与床面稳定性时，明确指出卵石结构化床面对床面的稳定性有着非常重要的影响。由此可见，在一定的水流条件下受到冲刷作用的卵石颗粒位置的调整将会增强其抗冲能力，卵石颗粒位置调整与床面泥沙颗粒粒径的变化伴随着冲刷粗化过程而进行。

以上分析表明:在床沙粗化程度较低时，床面细颗粒泥沙所受到的保护(荫蔽)作用较小，床面泥沙易于起动输移；随着粗化程度的增大，床面细颗粒受到的保护(荫蔽)作用增大，床面泥沙难以起动输移。因此在进行卵石河床推移质输移研究时，考虑粗化作用对卵石输移的影响是十分必要的。

3.3 现有的宽级配推移质输沙公式

在最初的宽级配非均匀沙输沙率研究中，学者们选用床沙中的某一级粒径作为代表粒径，然后运用均匀沙输沙率公式进行计算。Einstein[4]根据一些小河的实测资料即水槽试验资料结果，选用床沙中的D35(小于这个粒径的泥沙占总泥沙质量的35%)作为代表粒径，而Meyer-Peter等[2]则建议选用平均粒径Dm作为代表粒径。

随着研究的进一步深入，各家学者发现研究非均匀沙分组输沙率是很有必要的，近些年来关于这方面的研究比较多。Einstein[4]修正了流速和上举力系数，考虑了荫蔽作用对泥沙输移的影响，建立了非均匀沙分组输沙率公式；Bagnold[3]根据单位水流功率理论，研究了非均匀沙推移质输沙率；Parker[18]给出了起动标准，建立了基于床面表层泥沙的分组输沙率公式；Wilcock[6]在Parker[18]基础上进行了更深入的研究。国内关于推移质输沙率的研究也很多：卢金友等[19]根据长江上游的实测资料建立了非均匀沙输移的经验公式；徐海涛等[20]构造了考虑床沙不均匀特性的相对水流强度表达式，着重研究了相对水流强度与推移质输沙率函数的关系；魏丽等[21]对天然河段不连续宽级配床沙特性及形成条件进行了初步探讨，为不连续宽级配床沙运动规律研究提供了基础；刘兴年等[10]在研究非均匀沙输移时，考虑了床沙的粗化、细化对输移的影响，提出了粗化程度的概念，建立了考虑粗化程度的推移质输沙率公式。需要指出的是，在现有的推移质输沙率公式中，只有刘兴年公式[10]考虑了粗化对卵石河床泥沙输移的影响，有的公式虽然也考虑了粗化的影响，但在公式中没有明确反映。

然而，上述大多公式没有深入考虑粗化作用对泥沙输移的影响，分析各家公式可知，大多数公式仅需水流资料和床沙级配资料就可进行计算，没有直接反映粗化、细化对输沙影响的参数,这就使得这些公式不具备通用性，Gomez等[13]、Van Der Scheer等[14]、Reid等[15]的研究充分说明了这一状况。

刘兴年等[10]在研究非均匀沙推移质输沙率时，实测了非均匀床面的暴露度，指出暴露度并非均匀分布，在暴露度计算中引入了粗化程度参数A，A的取值范围为0～1。A趋于0时，床沙趋于刚发生粗化；A越大，床面粗化程度越大。事实上，河流均处于粗化过程中的某一程度，不会达到完全粗化状况，即粗化程度为1。刘兴年曾用青衣江梯子岩、都江堰资料反求得到2条河流的粗化程度参数A值在0.3～0.5之间。刘兴年公式的具体推导过程可见文献[10]。其公式可描述为

(2)

式中τci(A)为考虑了粗化程度影响的床沙起动临界切应力。

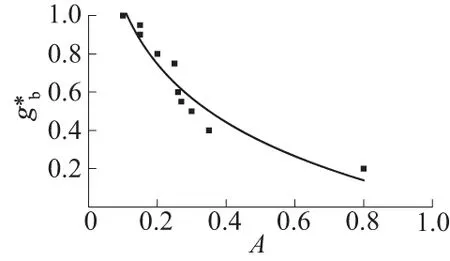
图2 粗化程度对相对推移质输沙率的影响Fig.2 Influence of coarse-ning degree on relative transport rate

探究各家推移质输沙率公式的研究过程可知，理论推导得出的大多公式中均有未定系数，这个系数要通过一定的实测资料验证获得，而试验资料中由于床沙性质的不同必然导致粗化程度不同，因此各家公式反映的实际是某一粗化程度下的推移质输沙规律。天然河流往往处于不同的粗化程度下，因此大多数公式的通用性就受到了制约。刘兴年公式引入的粗化程度参数对推移质输移研究来说具有重要的意义，值得进行更为深入的研究。

4 粗化层的稳定性对推移质输沙的影响

山区河流卵石河床表层大多为粗化层覆盖，粗化层的形成制约了冲刷的进一步发展，使得河床具有一定程度的稳定性。当水流强度不高时，床面仍会保持稳定；当水流强度较高时，粗化层就有被破坏的危险。下面介绍关于粗化层破坏的水槽试验现象和野外观测到的粗化层破坏现象。

4.1 粗化层破坏的水槽试验研究

试验是在四川大学水力学与山区河流开发保护国家重点实验室变坡水槽内进行的，为清水冲刷粗化层破坏试验。详细的试验条件可参见文献[22]。试验步骤如下：将一定级配的泥沙铺在床面上，释放一个较小流量的水流，以形成初始粗化床面，在此初始粗化床面条件下进行粗化层破坏试验，即不断小幅加大流量以增大水流强度，通过观察床面泥沙运动情况和输沙率的变化来判断床面粗化层的破坏情况，一直增大到床面粗化层破坏为止。其中A组次试验的单宽输沙率变化如图3所示。

图3 清水冲刷粗化层破坏试验单宽输沙率Fig.3 Bedload transport rate per unit width in the breakage of armoring layer

图3中，A0为形成初始粗化床面的过程，A1—A7流量逐渐小幅增大以加大水流强度。由图3可知，从A1—A6床面输沙率变化不大，床面可动颗粒较少，大颗粒基本不动；直到A7组次试验，床面输沙率陡增，床面可动颗粒很多，大颗粒也开始起动输移，粗化层遭到破坏。此类试验共进行了6组，总结6组试验资料得到了如下认识：①水流强度的增大并不一定能使一定水流条件下形成的粗化层床面结构破坏，只有当水流强度增大到一定程度，床面粗化层才会破坏；②粗化层床面结构对粗化层的稳定性有重要影响，粗化层的破坏将引起推移质输沙率的陡增，并导致河床发生剧烈演变。

在通常的推移质输沙率研究中，水流条件中床面切应力有着非常重要的作用，分析A组次试验的水流条件将有助于理解粗化层遭到破坏后输沙率的剧变过程，A组次试验水流条件如表1所示。

表1中，gb(0)指的是A0试验最后50 min的平均单宽输沙率，gb(1)至gb(6)指的是各阶段试验的平均单宽输沙率，gb(7)指的则是A7组试验的粗化层遭

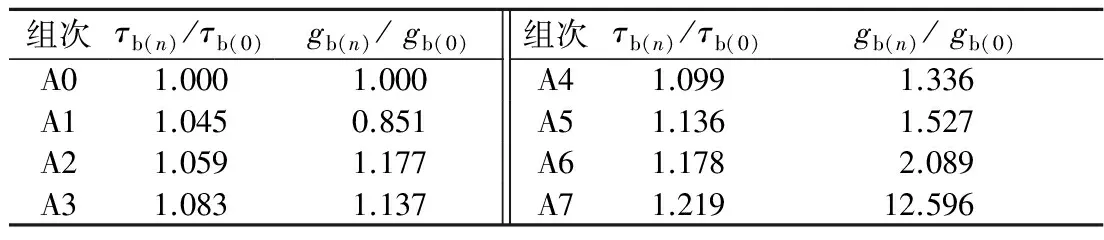
表1 A组试验切应力和单宽输沙率

到破坏时的最大单宽输沙率。比较分析可知，从A0—A7，在床面泥沙组成基本相同的情况下，切应力仅增大到1.219倍，输沙率却增大到12.596倍。A6至A7阶段试验现象更加明显，切应力增大到1.035倍，输沙率却增大到6.030倍之多，现有的输沙率公式均不能反映这一现象。

聂锐华等[23]通过水槽试验研究了粗化层破坏过程中的推移质最大输沙率，结果表明：清水冲刷条件下粗化层破坏过程中的推移质输沙率峰值相应的无量纲输沙强度随床面切应力的增大而增大，其增速较Meyer-Peter公式、Bagnold公式和Engelund公式[24]计算所得输沙率增速明显偏大。因此，在计算粗化层破坏条件下的推移质输沙率时，需要考虑由于粗化层破坏而导致的输沙率陡增，这样才能取得较好的计算结果。

4.2 野外观测的粗化层破坏现象

粗化层的破坏会引起河床的剧烈演变，多年来进行粗化层破坏野外观测的学者并不多。Vericat等[25]在研究Ebro坝下游卵石河床稳定粗化层的破坏和重建时，发现在稳定粗化层形成后，如果水流强度不是很大，则床面可起动的泥沙很少，相应的单宽输沙率也很小；只有当洪峰流量足够大时，床面才会有大量颗粒起动输移——粗化层遭到破坏。Vericat研究组在该河段调查研究的时间很长，而粗化层破坏的时间则在2002年12月份至2003年3月份。该次粗化层破坏过程的具体资料可见表2。

表2 Ebro坝下游的粗化层破坏现象

需要指出的是表2中所列的3个流量为洪峰流量，具体洪水流量过程图见文献[22]。试验河段的床沙表层中值粒径为37.1 mm，最大粒径为137.1 mm；床沙次表层中值粒径为15.9 mm。比较分析表明，在2002年12月份，粗化层稳定，床面单宽输沙率较小，推移质中值粒径为21 mm。到2003年2月份，洪峰流量最大，床面切力增加很多，单宽输沙率急剧增大，床面粗化层遭到破坏；此时，次表层的较细泥沙在失去了表层粗颗粒的保护之后，也进入运动状态，此时的推移质中值粒径为19 mm，小于粗化层破坏之前的推移质中值粒径。到2003年3月份，又来了一次洪峰，床面粗化层的破坏引起了床面输沙率的急剧增大，推移质中值粒径也有所减小。比较发现，2003年2月份和3月份的洪峰切力分别是2002年12月份的1.34倍和1.11倍，输沙率则分别增大到9.53倍和23.33倍。

众所周知，Meyer-Peter公式应用较为广泛，一般能满足计算需要。下面应用Meyer-Peter公式在这次粗化层破坏过程中进行推移质输沙率试算。试算中，床沙代表粒径分别采用推移质中值粒径和对应于2002年12月份洪峰的粒径(46.68 mm)。根据表2对应于2003年2月份的洪峰，由Meyer-Peter公式可得其单宽推移质输沙率应为31 g/(m·s)，然而实际测得的单宽输沙率为143 g/(m·s)，较计算所得大112 g/(m·s)，这正是由于粗化层破坏所引起的，这种现象是现有输沙率公式所不能反映的。

4.3 考虑粗化层稳定性的推移质输沙率公式

在无泥沙补给条件下，经过一段时间的冲刷以后，输沙率将逐渐变小，根据以往的研究，推移质输沙率最终将趋于0，此时床面形成稳定粗化层。根据图3的实测资料可知，在粗化层形成后直到粗化层遭到破坏，推移质输沙率较粗化层形成末段的推移质输沙率略大。式(2)可大致描述此区段内的推移质输沙特性。

粗化层稳定时，床面的粗化程度较大，在粗化层遭到破坏以后，床面粗化层颗粒之间的密实结构遭到破坏，床沙颗粒位置发生了较大变化。虽然床面泥沙颗粒级配变化不多，但粗化程度却大幅减小，亦即卵石粗化层的粗化程度不仅与泥沙级配有关，还与床沙之间的位置结构有关。在粗化层遭到破坏以后，床面的粗化程度可参照松散床面的粗化程度取值。尽管如此，粗化层破坏时的输沙率还是要远大于考虑了粗化程度公式的计算值，鉴于此，粗化层破坏时的推移质输沙率公式可用式(3)表示。

(3)

式中gbd指的是粗化层破坏所导致的额外输沙率。

尽管试验资料缺乏，还不能给出粗化层破坏时额外输沙率gbd的计算式，但前述2个试验现象表明，额外输沙率gbd是确实存在的，gbd的计算式有待于收集更多的试验资料后给出。式(3)给出了计算粗化层破坏时的简单物理图景，但更为重要的是如何研究判断稳定粗化层破坏的临界条件，只有确定了粗化层破坏条件，才能更准确地描述卵石河床的演变特性。

5 结 论

(1) 均匀卵石的输沙率的计算，只要根据水流条件和泥沙颗粒大小选用合适的公式，一般均可获得满意的结果。

(2) 粗化程度对于宽级配卵石河床推移质输沙率有着重要的影响，在相同的床沙级配和来水来沙条件下，输沙率随着粗化程度的增大而减小。现有的多数非均匀沙推移质输沙率公式，一般只能反映某种粗化程度下的推移质输沙特性，限制了这些公式的适用性。只有考虑了粗化程度影响的公式才能较好地反映宽级配推移质的输沙特性。

(3) 粗化层的稳定性对宽级配卵石河床的输沙率影响也很大，试验现象表明，在粗化层破坏过程中，床面切力微小的变化却引起了推移质输沙率的急剧增大，现有公式均不能反映此种现象。因此，计算粗化层破坏后的输沙率时，有必要考虑额外输沙率。

(4) 前述分析表明，卵石河床的推移质输沙率计算与床面的粗化程度和粗化层的稳定性有着密切的关系，卵石河床推移质输沙率之所以难以准确描述，正是河床粗化所导致的。因此，如何确定卵石河床的粗化程度及稳定粗化层的破坏条件值得进行更为深入的研究。

[1] DUBOYS P. Le Rhne et Les Rivières à Lit Affouillable[J].Annales des Ponts et Chaussées, 1879, 18(5): 141-195.

[2] MEYER-PETER E, MÜLLER R. Formula for Bed-load Transport[C]∥Proceedings of 2nd Meeting, International Association for Hydraulic Research.Stockholm, June,1948: 39-64.

[3] BAGNOLD R A. An Approach to the Sediment Transport Problem from General Physics[R]. U.S.：U.S. Geological Survey Profession Paper 422-I, 1966:37.

[4]EINSTEIN H A. Bed Load Transport as a Probability Problem[D]. Colorado: Colorado State University,1937.(in German).Translated by SAYRE W W, in Sedimentation, Appendix C, 1972.

[5] PARKER G, KLINGEMAN P C, MCLEAN D G. Bedload and Size Distribution in Paved Gravel-bed Streams[J]. Journal of the Hydraulics Division, 1982, 108(4): 544-571.

[6] WILCOCK P R. Toward a Practical Method for Estimating Sediment Transport Rates in Gravel-bed Rivers[J]. Earth Surface Processes and Landforms, 2001, 26(13):1395-1408.

[7] 韩其为.泥沙起动规律及起动流速[M].北京：科学出版社，1999.

[8] 秦荣昱，王崇浩.河流推移质运动理论及应用[M].北京：中国铁道出版社，1996.

[9] 孙志林，田 林.非均匀沙分级推移质公式[J].水利学报，2001，(5):65-70.

[10]刘兴年，黄 尔，曹叔尤，等.宽级配推移质输移特性研究[J].泥沙研究，2000，(4)：14-17.

[11]钱 宁. 推移质公式的比较[J].水利学报，1980，(4):1-11.

[12]曹叔尤，刘兴年，方 铎，等.山区河流卵石推移质的输移特性[J].泥沙研究，2000，(4)：1-5.

[13]GOMEZ B, CHURCH M. An Assessment of Bed Load Sediment Transport Formulae for Gravel Bed Rivers[J]. Water Resources Research，1989，25(6):1161-1186.

[14]VAN DER SCHEER P，RIBBERINK J S，BLOM A. Transport Formulas for Graded Sediment，Behavior of Transport Formulas and Verification with Experimental Data[M]. Enschede: Civil Engineering University of Twente，The Netherlands，2002.

[15]REID I, LARONNE J B, POWELL D M. The Nahal Yatir Bedload Database: Sediment Dynamics in a Gravel-bed Ephemeral Stream[J]. Earth Surface Processes and Landforms, 1995, 20(9):845-857.

[16]HASSAN M A，CHURCH M. Experiments on Surface Structure and Partial Sediment Transport on a Gravel Bed[J]. Water Resources Research，2000，36(7)：1885-1895.

[17]WITTENBERG L，NEWSON M D. Particle Clusters in Gravel-bed Rivers: an Experimental Morphological Approach to Bed Material Transport and Stability Concepts[J]. Earth Surface Processes and Landforms，2005，30(11):1351-1368.

[18]PARKER G. Surface-based Bedload Transport Relation for Gravel Rivers[J]. Journal of Hydraulic Research，1990，28(4):417-436.

[19]卢金友，金中武，郭 炜，等.长江上游推移质泥沙输移研究[J].长江科学院院报，2009，26(1)：5-8.

[20]徐海涛，卢金友，刘小斌.不连续宽级配床沙推移质输沙率特性试验分析[J].长江科学院院报，2011，28(10)：26-30,36.

[21]魏 丽，卢金友，徐海涛.天然河道不连续宽级配床沙特性及形成条件探讨[J].长江科学院院报，2012，29(10)：6-10,15.

[22]王 涛，刘兴年，黄 尔，等.卵石河床清水冲刷粗化层破坏临界条件试验研究[J].四川大学学报(工程科学版)，2008，40(4)：36-40.

[23]聂锐华，刘兴年，杨克君，等.粗化层破坏过程中的最大推移质输沙率试验研究[J].四川大学学报(工程科学版)，2013，45(2)：1-5.

[24]ENGELUND F，FREDSØE J. A Sediment Transport Model for Straight Alluvial Channels[J]. Hydrology Research，1976，7(5)：293-306.

[25]VERICAT D，BATALLA R J，GARCIA C. Breakup and Reestablishment of the Armour Layer in a Large Gravel-bed River below Dams: The Lower Ebro[J].Geomorphology，2006，76(1/2)：122-136.

(编辑：罗 娟)

Characteristics of Bed-load Transport in Gravel Bedof Mountain Rivers

CAI Bing-yun

(Sichuan Branch, Shanghai Investigation，Design & Research Institute Co.，Ltd.，Chengdu 610000，China)

Surface layers of gravel bed of wide gradation are usually covered by armoring layer with different coarsening degrees. Most of the existing bed-load transport formulas could just reflect the characteristics of sediment transport in a certain coarsening degree, hence are of poor applicability. Theoretical analysis and experiment results show that bed-load transport rate decreases as the coarsening degree of armoring layer increases under the same incoming flow and sediment condition. Introducing the parameter of coarsening degree into the calculation could solve this problem. The stability of armoring layer plays an important role in bed-load transport in gravel bed. Bed-load transport rate increases sharply when the armoring layer is broken. The calculation results of the existing formulas are obviously small. Therefore, the sharp increase of sediment transport rate caused by the failure of armoring layer should be considered in calculating the bed-load transport rate.

gravel bed；bed-load transport rate；coarsening degree；stability of armoring layer；critical conditions

2016-04-12；

2016-06-22

蔡炳云(1981-)，男，河北辛集人，工程师，硕士，研究方向为水力学及河流动力学，(电话)18180865605(电子信箱)41909015@qq.com。

10.11988/ckyyb.20160343

2017,34(7):1-6

TV142

A

1001-5485(2017)07-0001-06