条件先验概率优势关系粗糙集模型

陶 志，何丹峰，潘丽平

（中国民航大学理学院，天津 300300）

条件先验概率优势关系粗糙集模型

陶 志，何丹峰，潘丽平

（中国民航大学理学院，天津 300300）

基于先验概率优势关系的粗糙集模型是对粗糙集理论的重要扩充，然而却有其不足之处。本研究提出的基于条件先验概率优势关系的粗糙集模型是建立在对不完备偏序关系决策系统属性值数据统计的基础上，既考虑到同一属性取值的不同情况又考虑到不同属性之间的关联性，充分利用各种先验信息，因此有效提高了分类精度和分类质量。理论分析和实例计算均证明了该模型的有效性和实用性。

粗糙集；不完备偏序关系决策系统；条件先验概率优势关系

粗糙集理论自在1982年被波兰学者Z Pawlak[1]提出以来，已被普遍使用于处理各种不完整和不确定性问题。然而，Pawlak所提出的经典粗糙集理论只适用于完备的信息系统，并且将属性看作常规属性（属性值之间不具有优劣顺序）。事实上，由于数据缺失和受人们主观偏好的影响，在许多实际问题中碰到更多的是含有偏序关系的不完备信息系统，为处理这一问题，Greco等[2]提出了基于优势关系的粗糙集模型，这是人们首次在多属性分析决策问题中使用优势关系而非等价关系。在此之后，针对带有偏序关系的多准则不完备信息系统，学者们又给出许多新的优势关系模型。例如，扩展优势关系模型[3]和限制扩展优势关系模型[4]，但前者过于宽松，后者的要求又过于严格，均有自身的局限性。同时，由于上述模型都没有考虑已知信息对未知属性值的影响，因此普遍存在分类精度不高、分类不尽合理等方面的不足。针对这些情况，有学者提出了先验概率优势关系[5]粗糙集模型和加权先验概率优势关系[6]粗糙集模型。但是，这些利用先验信息来推测未知属性值的粗糙集模型均只单方面考虑了属性值之间的关系，忽视了属性与属性之间的关联性，具有某种局限性。实际上在含有偏序关系的不完备决策系统中，条件属性间经常是具有某种关联关系存在的，例如，某高中生的化学成绩由于某种原因缺失（缺考或其他原因），那么应如何判断其化学成绩所属的可能等级，如果仅仅根据所有学生化学成绩出现概率最大的那一等级来划分，显然不太合理，因为如果这名学生擅长理科，那么其理科类成绩会比文科类成绩更好，于是他的数学、物理等这些理科成绩也是判断其化学成绩的关键因素。此例表明，为了更加准确地补充未知属性值的数据信息，在处理不完备系统中的先验知识时还应该充分考虑对象本身已给出的其它属性值[7-8]信息。

本文提出了以不同属性之间的相互关系为基础的条件先验概率优势关系粗糙集模型，并对这一模型的特点和性质进行了分析和讨论。新模型与其他已有的先验概率优势关系模型相比提高了分类精度和分类质量，为在含有偏序关系的不完备偏好决策系统中进行规则的提取和优化提供了一种更加合理且有用的手段。

1 基本知识

1.1 不完备偏序关系决策系统

一般地，用四元组 S=（U，AT=C∪D，V，f）表示一个含有偏序关系的决策系统，U是包含有限对象的非空集合；AT=C∪D是包含所有属性的非空属性集，其中条件属性集用C表示，决策属性集用D表示；V表示属性值集，VC={Vq∶q∈C}与 VD={Vd∶d∈D}分别表示带有偏序关系的条件属性值与决策属性值集；f∶U×AT→V表示一个信息函数，即对每个a∈AT，x∈U，都有f（x，a）∈Va。若存在一个x∈U，a∈C使得f（x，a）=*（*代表缺损值），则称S是一个含有偏序关系的不完备决策系统（简称不完备偏序关系决策系统）。

对于上述不完备偏序关系决策系统，可假定以下2种情况：

1）Vd不含有任何空值；

2）∀x∈U，至少有一个属性q∈C存在，使得f（x，q）≠*。

假设D={d}，其中U被d分成有限个决策类，Cl={Clt，t∈T}，T={1，2，…，n}，则∀x∈U，x 属于且只能属于一个Clt。而且，假设这种对象间的划分是按照一定次序，即∀r，s∈T，如果 r＞ s，则 Clr中的每一个对象就不劣于Cls中的每一个对象，如果x∈Clr，y∈Cls，记为xDy。

同时，针对每个决策类给出向上累积集和向下累积集的定义如下：

上述定义[3]表明，如果，则 x至少属于 Clt；如果，则 x至多属于 Clt。

由定义1可得到如下性质[3]：

1.2 先验概率优势关系

文献[5]在不完备偏序关系决策系统中引进先验概率优势关系的概念，从而可利用已知统计信息对缺损值进行推断。

定义2 若S=（U，AT=C∪D，V，f）为一个不完备偏序关系决策系统，集合A⊆C，x，y∈U，则A上的先验概率优势关系FDOM（A）定义[5]为

式中

其中：Vq={v1，v2，…，vm}是 q 的值域是Vq中属性q取不同属性值的概率。如果有对象x、y满足上述关系，亦称“y先验概率优势于x”，简记为

显然，在上述模型中“*”的可能取值是依据Vq中出现次数最多的属性值来推断的（最大可能准则），其忽略了其他不同属性取值对其可能产生的影响，因此容易出现信息利用不充分使得分类结果出现较大误差的现象。

针对此问题，下节将给出条件先验概率的概念，条件先验概率不仅考虑了同一属性取值对空值“*”的影响，而且还对属性之间的关联性信息加以提取和利用，使得不完备偏序关系决策系统中对象的划分更加精细和准确，分类质量和分类精度也得以提升。

2 条件先验概率优势关系粗糙集模型

2.1 条件先验概率

若在不完备系统中实现对象间的合理分类，需详细分析系统中的每个属性，特别需注重分析这些属性间的相互联系。

若 S=（U，AT=C∪D，V，f）为一个不完备偏序关系决策系统，则∀x∈U，A⊆C，对于对象x，属性集A可分为以下两类：

下面给出条件先验概率的定义。

定义 3 设 S=（U，AT=C∪D，V，f）为一个不完备偏序关系决策系统，为属性的值域

则属性ai=vij的条件先验概率定义为

条件先验概率是指某一对象x在其确定性属性取值已经发生且不变的情况下，其非确定性属性取某一值的概率。条件先验概率考虑了属性间的内在影响，比较先验概率而言可提供相对充分的统计信息。

2.2 条件先验概率优势关系

依据条件先验概率的定义，在不完备偏序关系决策系统中给出了新的条件先验概率优势关系的概念如下：

定义 4 设 S=（U，AT=C∪D，V，f）为一个不完备偏序关系决策系统，集合A⊆C，x，y∈U，A上的条件先验概率优势关系HFDOM（A）定义为

式中

条件先验概率优势关系是通过属性间的内在联系来推测未知属性值，进而对对象之间的优劣关系进行合理而准确的划分。由定义我们可以证明，条件先验概率优势关系满足传递性和自反性，但是不满足对称性。

定义5 设S=（U，AT=C∪D，V，f）是一个不完备偏序关系决策系统，则对于A⊆C，x∈U，称为A的条件先验概率优势集；称为A的条件先验概率劣势集。

某对象x的条件先验概率优势集是由所有依A的条件先验概率优势关系“优于”x的对象所构成的集合，而x的条件先验概率劣势集是由所有依A的条件先验概率优势关系“劣于”x的对象所构成的集合。

定理 1 设 S=（U，AT=C∪D，V，f）为一个不完备偏序关系决策系统，在条件先验概率优势关系下：

2）证明方法同 1）。

证毕。

上述定理指出了条件先验概率优势集与劣势集之间的关系。

2.3 基于条件先验概率优势关系的粗糙近似

Clt为给定的某一决策类，对于Clt的向上、向下累积集，下面给出基于条件先验概率优势关系的粗糙近似的定义。

定义6 设S=（U，AT=C∪D，V，f）为一个不完备偏序关系决策系统分别表示Clt的向上累积集和向下累积集，则的基于条件先验概率优势关系的粗糙上、下近似集及边界域分别为

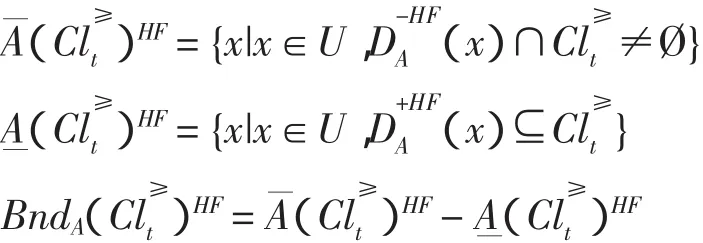
定理2 设S=（U，AT=C∪D，V，f）为一个不完备偏序关系决策系统，A⊆C，x∈U，则在条件先验概率优势关系下有：

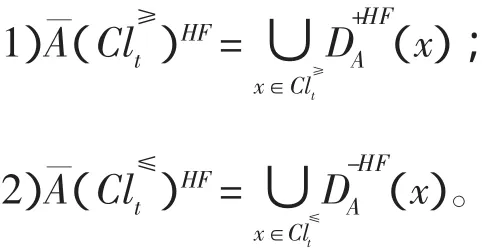
证明 由定理1和定义6可直接证明。

定义7 设S=（U，AT=C∪D，V，f）为一个不完备偏序关系决策系统1，2，…，n，则在条件先验概率优势关系下的粗糙近似分类精度分别为

分类精度表示对某一确定的决策类，依条件先验概率优势关系对对象进行分类时，可能的决策中正确决策的百分比，也是系统针对某一确定决策分类精度的一个度量。

定义8 设S=（U，AT=C∪D，V，f）为一个不完备偏序关系决策系统1，2，…，n，则在条件先验概率优势关系下的粗糙近似分类质量可被定义为

分类质量是衡量带有偏序关系的不完备决策系统中总体对象分类精度的一种方法。

3 实例分析

表1所示为某中学学生的身体素质测评结果，每名学生身体素质测评标准的条件属性集是A={a1，a2，a3，a4，a5}，决策属性集为 D={d}，其中，a1、a2、a3、a4、a5表示 5 种课程，d 是学生的综合测评，a1、a2、a3、a4、a5、d 均为偏好属性，其中，Vai={1，2，3}，i=1，2，…，5，1＜2＜3，表示单科成绩 ai所属的等级，Vd= {1，2，3}，1＜2＜3，表示学生综合测评等级。条件属性值的先验概率分别为。决策属性 d 把对象划分为 3 个决策类，Cl={Cl1，Cl2，Cl3}，其中

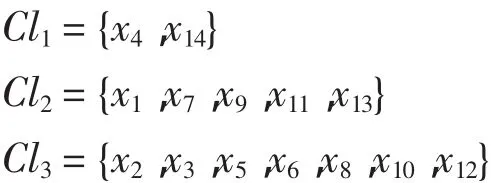
则有

表1 不完备偏序关系决策系统Tab.1 Incomplete partial order relation decision system

利用先验概率优势关系粗糙决策模型进行分类计算，其结果如下

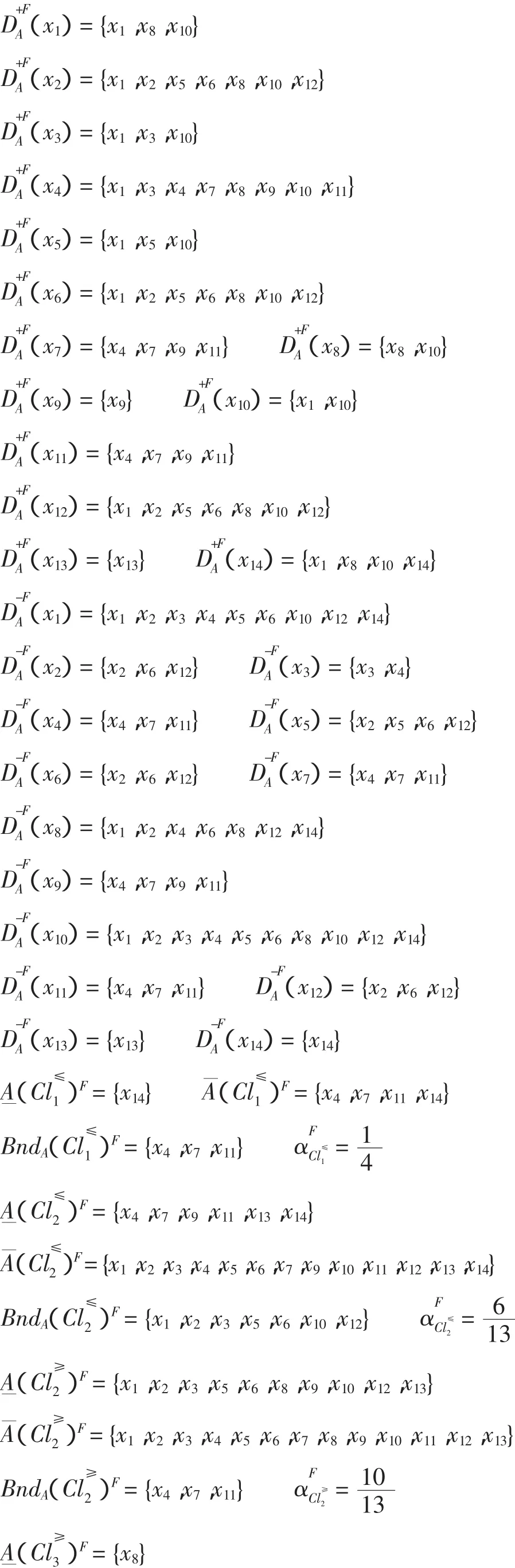
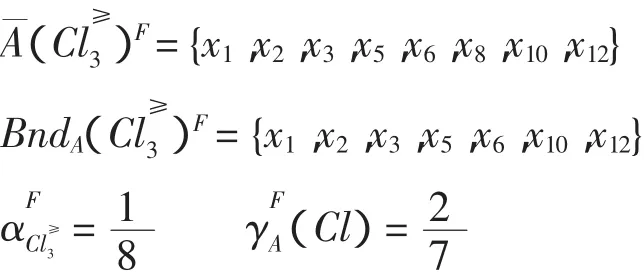
利用条件先验概率优势关系粗糙决策模型分类计算，其结果如下

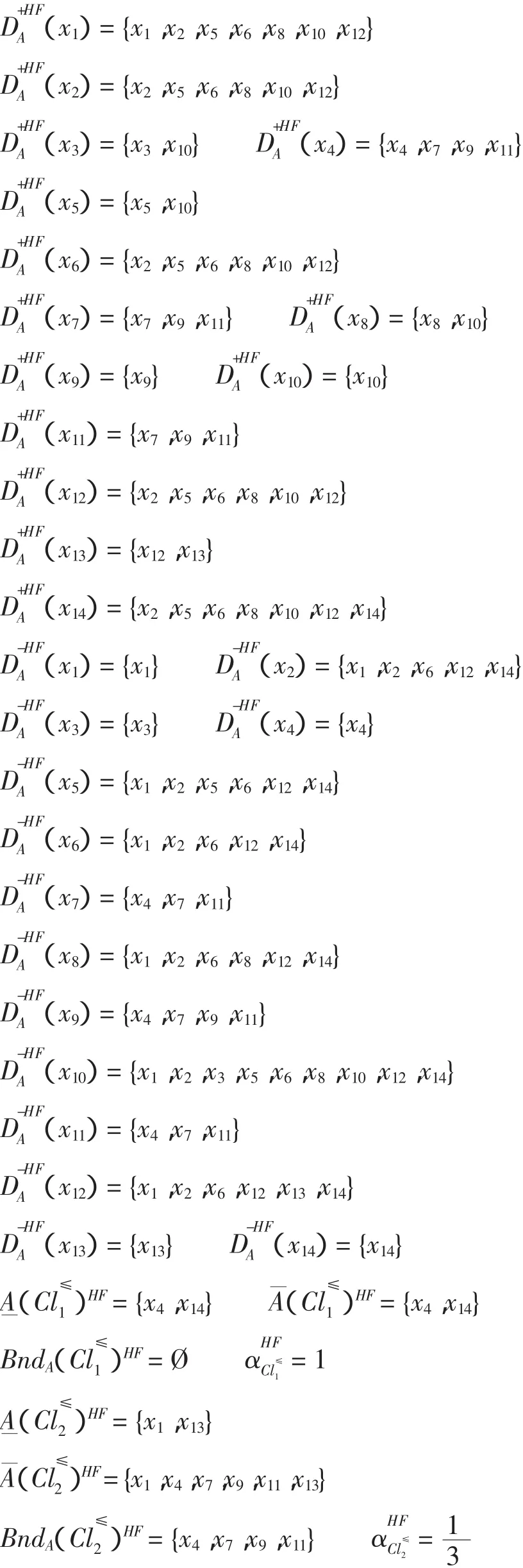
从以上计算可看出，按先验概率优势关系可推断x1优于x2，而这与两者的决策属性取值正好相反，这种偏差是由于先验概率优势关系忽略了条件属性间的内在联系所造成的。然而，由条件先验概率优势关系可推断出x2优于x1，这恰好与实际已发生的数据结果相符。另外，由先验概率优势关系无法推断对象x4和x11的优劣关系，而由条件先验概率优势关系可推知x11优于x4，这也与决策属性的取值结果相符。上述实例充分说明，条件先验概率优势关系模型比先验概率优势关系模型分类更加精细，减少了不确定性。同时，从分类精度和分类质量的计算结果比较来看，也进一步说明此结论是正确的。

4 结语

基于条件先验概率优势关系的粗糙集模型是在分析了先验概率优势关系粗糙集模型的缺点和不足后，所提出的在不完备偏序关系决策系统中对对象间优劣关系进行划分的一种新方法。新模型充分利用了不完备偏序关系决策系统所提供的各种先验信息，使得数据分类更加准确和精细。在处理属性间存在内在关系且未知属性值相对较少的大规模数据信息时，新模型具有明显优势。理论分析和实例计算均说明，新模型克服了传统先验概率优势关系模型的缺点和不足，并且提供了一种更加接近于实际决策过程的粗糙决策新方法。

[1]PAWLAK Z.Rough set[J].International Journal of Computer and Information Science,1984,11：341-356.

[2] GRECO S,MATARAZZO B,SLOWINSKI R.Rough sets theory for multicriteria decision analysis[J].European Journal of Operational Research,2001,129(1)：1-47.

[3] 何亚群,胡寿松.不完备信息的多属性粗糙决策分析方法[J].系统工程学报,2004,19(2)：117-120.

[4] 骆公志,杨晓江,周德群.基于限制扩展优势关系的粗糙决策分析模型[J].系统管理学报,2009,18(4)：391-396.

[5] 陶 志,卞文静.基于先验概率优势关系的粗糙决策分析模型[J].中国民航大学学报,2013,31(4)：60-64.

[6] 骆公志,李 震,黄卫东.加权先验概率优势关系的粗糙决策分析模型[J].统计与决策,2015(20)：67-70.

[7] 陶 志,刘彩平.一种改进的先验概率粗集模型[J].中国民航大学学报,2014,32(4)：48-51.

[8]TAO ZHI,HU SHUQIN,GUAN JING.Rough set model with tolerance relation based on conditional prior probability[J].Applied Mechanics and Materials,2014,687：1312-1315.

（责任编辑：杨媛媛）

Rough set model based on conditions prior probability dominance relation

TAO Zhi,HE Danfeng,PAN Liping
（College of Science,CAUC,Tianjin 300300,China）

Rough set model based on prior probability dominance relation is an important expansion of rough set theory.However,it has its own defects and shortcomings.Rough set model based on conditions prior probability dominance relation is established on the basis of attribute value data statistics of incomplete partial order relation decision system.It not only takes into account different conditions of the same attribute values,but also the correlation between different attributes,so that a variety of prior information can be fully utilized.Therefore,the classification accuracy and quality can be improved effectively.This new model is proved to be effective and practical by theoretical analysis and practical example.

rough set;incomplete partial order relation decision system;conditions prior probability dominance relation

TP18

A

1674－5590（2017）03－0059－06

2016-09-18；

2016-11-23

国家自然科学基金项目（60672178）；中国民航大学科研基金项目（2010kys01）

陶志（1963—），男，辽宁沈阳人，教授，博士，研究方向为复杂系统建模、粗糙集理论及其应用等.