应急电源系统平均寿命Bayes估计方法研究

赵 权，葛红娟，张 璐，林 怡

（南京航空航天大学民航学院，南京 211106）

应急电源系统平均寿命Bayes估计方法研究

赵 权，葛红娟，张 璐，林 怡

（南京航空航天大学民航学院，南京 211106）

提出了一种元器件应力分析和综合E-Bayes理论相结合的平均寿命预估方法，该方法基于定时截尾试验获取的无失效数据，利用元器件应力研究结果作为失效数据输入量，使得综合E-Bayes两个输入相互解耦，解决了失效数据对无失效数据的直接依赖以及与产品性能关联性弱的问题。本研究将该方法用于C919飞机应急电源系统，推导了系统平均寿命的Bayes预计模型，同时将预估结果与传统综合E-Bayes法进行比较。分析表明，使用本研究提出的综合E-Bayes算法得到的系统平均寿命预估值极差范围更小，对参数选择的稳健性更好。

平均寿命；综合E-Bayes；元器件应力分析；定时截尾试验；稳健性

应急电源系统[1]是在飞机试飞过程中用于对测试设备进行供电的系统。系统可靠性直接影响试飞工作的进程。目前，C919-102架机应急电源系统失效率规定为10-6级，综合分析和估计该应急电源系统可靠性是非常必要的。

民航高可靠性电子设备或系统，在有限的可靠性试验中，往往会出现无失效的情况。

Bayes[2]在失效数据[3]和无失效数据[4-10]的分析中具有重要的使用价值。国内常用的有经验贝叶斯（EBayes）[6，10]和综合 E-Bayes 法[6-8，10]。韩明[9]提出运用增函数法和减函数法构造先验分布，但单调先验往往不符合经验信息；郭金龙[10]将综合E-Bayes法应用到船舶的可靠性研究中，失效数据输入依赖无失效数据，无失效数据的随机性往往会对预估结果造成不良的影响。

本文提出基于元器件应力分析的综合E-Bayes估计方法，该方法采用单调先验，并利用元器件应力分析引入失效信息，提高了寿命估计结果与产品性能的关联性；该方法在中国民机C919-102架机应急电源系统平均寿命估计中得到应用研究，并与传统综合E-Bayes法进行比较分析，验证了该方法的稳健性。该方法可用于其他民用航空设备的寿命估计或延伸到其他可靠性指标的分析中。

1 失效信息与可靠度函数拟合

图1给出了C919-102架机应急电源系统结构图[1]。其由重要设备、一般设备和专项设备3个供电通道构成，每个通道由蓄电池组作为备份，系统根据型号要求具有多种工作模式，本文将以双发工作模式下的重要设备供电通道（后以应急电源系统代指）为例进行平均寿命估计的应用研究，系统重要设备的失效率指标数量级为10-6。其工作原理如下：正常情况下，变压整流器TRU1为重要设备供电并给蓄电池组BAT1充电；TRU1支路故障时，由BAT1组件为设备供电。TRU1支路包括TRU1电源控制单元、TRU1、接触器C3、二极管D4；BAT1组件包括蓄电池组BAT1及其充放电控制模块以及二极管D1。

1.1 基于元器件应力分析的系统失效信息

元器件应力分析可靠性预计法[11]认为，除微电路外，大多数元器件的工作失效率λp的预计模型都为基本失效率λb与πE、πQ等一系列π系数相乘的形式。根据器件工作环境、器件结构以及电流电压等工作电参数[1]，查阅GJB/Z 299C-2006《电子设备可靠性预计手册》，得到部分器件失效率信息如表1所示。

表1 元件失效率预计Tab.1 Failure rate prediction of components

系统断路器和熔断器采用进口器件[1]，失效率分别为 0.680 × 10-6/h[11]和 0.026 × 10-6/h[11]，接触器 C1、C3失效率取10-7/h[1]，TRU自主设计，失效率取10-6/h[1]。自开封之日，GNC系列航空蓄电池组BAT1（购买）失效率为0.402×10-6/h[1]。鉴于控制器件的影响，取蓄电池模块失效率为10-6/h。考虑器件性能和应用特征，蓄电池组件在整个寿命周期都承受一定的等效工作应力，如二极管失效率估计时，同时考虑了反向电压应力和正向导通电流应力的影响。此外，系统工作模式的正常切换，也将使该部分循环作为正常工作单元，因而在进行安全性分析中，不能将其看成单纯的备用冗余，而应当做并联结构进行分析。由计算可得BAT1组件失效率λB=1.043 5×10-6/h，TRU1支路失效率λT=2.870 8×10-6/h。系统可靠度为

1.2 系统可靠度函数拟合

一般电气设备和电子设备等多属于复杂设备。根据复杂设备的故障定律和实际运行经验，可认为系统整体故障率为常数，即符合指数分布。

在Matlab中用最小二乘法对Rs（t）进行曲线拟合，拟合模型为指数分布。

拟合后的可靠度函数为

图2 可靠度函数拟合前后对比图Fig.2 Comparisonfigureofreliabilityfunctionbeforeandafterfitting

2 基于应力分析的综合E-Bayes算法

由前述可知，系统寿命符合指数分布e（1/θ），参数θ为系统平均寿命。

取θ的先验分布为逆伽马分布，其密度函数为

其中：0<θ<+∞，a和 b 为超参数，且 a>0，b>0，Γ（a）=为Γ函数。

由于系统失效率低，因而推测θ的先验密度函数存在一个较大的极值点σ，当θ<σ时，θ的先验密度核为增函数，当θ>σ时，先验密度核为减函数。现对π（θa，b）进行一阶求导

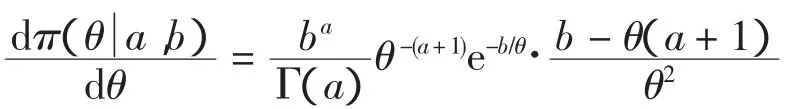
为取得较大的σ，a值应该较小，尺度参数b应大于产品实际寿命，同时考虑到Bayes估计的稳健性，b值不应该过大，a不应该过小。使E（θ）有限并以b为上界，此处取a的常数先验为区间[2，c]上的均匀分布U（2，c）。下面分析中将固定 b、c。

现对系统进行k次定时截尾试验，试验时间为ti（i=1，2，…，k），若未到规定时间即出现故障，则维修或更换后继续试验。假设第i次试验中，出现了ri次失效，则ri符合参数为的泊松分布[8]，即

由于系统失效率较低，故在有限的试验中常会出现无失效数据的情况。若前k次定时截尾试验中，无一失效。则θ的似然函数为

其中

当样本分布为泊松分布P（θ）时，θ的共轭先验分布族为伽马分布族[2]。由Bayes后验密度定义求θ的后验密度核

添加一个正则化常数因子可得θ的后验分布为

平方损失函数 L（θ，η）=（θ- η）2，现计算贝叶斯解。

由文献[2]可知，平方损失下θ的Bayes估计为后验均值，即

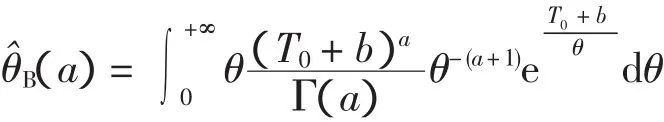
得

当 a的常数先验为区间[2，c]上的均匀分布 U（2，c）时，θ的E-Bayes估计为

现假设进行第k+1次定时截尾试验（事实上并没有做），试验时间为tk+1，期间共出现了rk+1次失效，则θ的似然函数为

由共轭分布的性质[2]求得引入失效数据后θ的后验分布为

在平方损失函数 L（θ，η）=（θ- η）2的条件下，计算的期望即为θ的贝叶斯解，可得

考虑a的常数先验为区间[2，c]上的均匀分布，则引入失效信息后θ的E-Bayes估计为

下面分析rk+1可能的取值情况。由于系统失效率低，Bayes理论认为第k+1次定时截尾试验中，系统至多发生一次失效，即假设系统在某个时间点发生第一次失效后，马上进行维修或更换，然后继续试验，系统在剩余试验的时间内，不会再发生失效。由此，rk+1只能在0和1中取值。取权重ω（rk+1）对θˆEB（rk+1）进行加权。定义系统平均寿命的综合E-Bayes估计[6，8]为

由于系统寿命符合指数分布，则认为ω（0）=e-1，取近似得并将式（7）和式（11）代入得

3 应急电源系统平均寿命估计

现获得C919-102架机应急电源系统的一组定时截尾试验数据，如表2所示，试验期间没有发生失效。由表2得

表2 系统无失效试验数据Tab.2 Zero-failure test data of system

引入失效数据tk+1后，可计算总定时截尾时间T=用应力分析得到的寿命估计值模拟式（2）计算的E（θ），根据本文第2节对参数b、a的分析，让b在2倍的E（θ）附近取值，同时可得a的上界c≥3，则分别取b为1.6×106、1.8×106、1.9 × 106、2.0× 106、2.1 × 106，分别取 c=3.2、3.4、3.6、3.8、4.0，根据式（13）计算系统平均寿命θˆSA-SEB，计算结果如表3所示。

表3应急电源系统平均寿命θˆSA-SEB（×106h）Tab.3Mean life θˆSA-SEB（×106h）of emergency power supply system

从表3中可以看出，系统平均寿命预估值符合技术要求，且大于简单应力分析结果。当b、c取值变化时，系统寿命估计值极差较小，说明该方法具有较好的稳健性。极差大小与b、c取值有关，b值增大，极差增大；而c值增大时，极差变小，这与本文第2节中对参数b、c的分析一致。

4 平均寿命预估算法比较

针对C919应急电源系统，将本文提出的方法与传统的综合E-Bayes法进行比较。传统的综合EBayes算法[6-9]中，第k+1次定时截尾试验的时间、权重表达式分别为同理将式（7）和式（11）代入式（13）可得

由表2可算得tk+1=1 448 h，则

表4应急电源系统平均寿命θˆSEB（×106h）Tab.4Mean life θˆSEB（×106h）of emergency power supply system

为更好地比对本文提出的基于元器件应力分析的综合E-Bayes法和传统综合E-Bayes法（下图中分别用SA-SEB和SEB标注）在不同b、c值下对系统平均寿命的预估情况，绘制了图3所示的系统平均寿命三维图。图4和图5分别是参数b、c在不同取值下对应的系统平均寿命极差图。

1）从图3中可以看出，基于应力分析的综合EBayes法得到的应急电源系统平均寿命估计值要高于传统的综合E-Bayes法，这是因为后者引入的失效数据tk+1依赖较小的无失效数据，从而导致预估结果偏小。

图3 应急电源系统平均寿命三维图Fig.3 3D mean life diagram of emergency power supply system

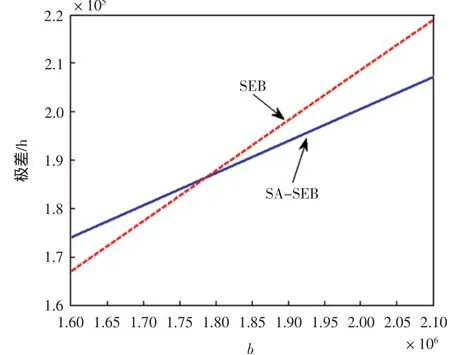
图4 不同b值对应下的系统平均寿命极差Fig.4 Range of mean life under b

图5 不同c值对应下的系统平均寿命极差Fig.5 Range of mean life under c

2）从图4中可以看出，在b取值范围内，两种方法因c值变化得到的系统平均寿命极差相近，这说明两种方法对c值选择的稳健性相当。

3）观察图5可以看到，当c为取值范围内任意值，b值在选择范围内变化时，基于应力分析的综合EBayes法得到的平均寿命极差更小，这说明该方法对b值选择的稳健性要好于传统的综合E-Bayes法。综合图4和图5，认为本文提出的基于应力分析的综合EBayes法稳健性更优。

5 结语

综合E-Bayes算法中无失效数据具有一定的人为随机性，本文基于解耦思想，从应力分析结果引入失效数据，提高了评估结果与产品性能的关联性。本文将该方法用于C919-102架机应急电源系统，并针对先验分布超参数b、c取值变化对预估稳健性的影响，与传统综合E-Bayes法进行比较，结果表明本文提出的方法具有更好的参数选择稳健性。在民用航空领域，电子设备或系统往往具有较高的可靠性，利用本文思想和方法，可进行航空电子设备或系统相关可靠性性能的分析工作，利用民航统计数据，可进一步规范相关超参数的选取标准。针对可能出现的“冒进”问题，可在应力分析阶段，适当对设备/系统可靠性结构或性能降级，不过应当基于经验和相关历史数据合理进行。

[1]试飞中心测试配电系统方案[Z].南京：南京航空航天大学,2015.

[2] 韦来生,张伟平.贝叶斯分析[M].合肥：中国科学技术大学出版社,2013.

[3] GUIDA M,PENTA F.A Bayesian analysis of fatigue data[J].Structural Safety,2010,32(1)：64-76.

[4] MIACHEL V.Practical Bayesian Methods for Determining Device Failurerates from Zero-Failure Data[C]//Reliability and Maintainability Symposium(RAMS),Orlando,FL,USA,2013.

[5]XIA X.Reliability analysis of zero-failure aata with poor information[J].QualityandReliabilityEngineeringInternational,2012,28(8)：981-990.

[6]刘永峰.Bayes方法在无失效数据可靠性中的若干应用[D].温州：温州大学,2011.

[7] 徐天群,刘焕彬,陈跃鹏.无失效数据情形失效率的综合E-Bayes估计[J].数理统计与管理,2011,30(4)：645-654.

[8] 姜丁源.指数分布下无失效数据情形参数的综合估计[D].长春：吉林大学,2007.

[9]韩 明.先验分布的构造方法在无失效数据可靠性中的引用[J].运筹与管理,1998,7(4)：27-29.

[10]郭金龙.基于无失效数据船体可靠性的研究[D].哈尔滨：哈尔滨工程大学,2009.

[11]GJB/Z 299C-2006,电子设备可靠性预计手册[S].北京：中国人民解放军总装备部,2006.

（责任编辑：杨媛媛）

Bayesian estimation for mean life of emergency power system

ZHAO Quan,GE Hongjuan,ZHANG Lu,LIN Yi
（College of Civil Aviation,Nanjing University of Aeronautics and Astronautics,Nanjing 211106,China）

A tool combining with components stress analysis and synthetic E-Bayes theory is proposed to deal with the mean life of complex aeronautical electronics with the intention to handle the nondecoupling for the inputs of traditional synthetic E-Bayes.It is done with the truncation time of terminated testing as zero-failure data and the result of the components stress analysis as the failure data which is aimed to solve the direct dependence on zero-failure data and little relationship with practical performance for failure data.The computational formula of the mean life is deduced when the tool is used in the emergency power system of C919 airplane.To research the robustness,this tool is compared with the traditional synthetic expected Bayesian.As a result,the foregoing shows a better robustness.

mean life;synthetic E-Bayes;component stress analysis;terminated testing;robustness

V216

A

1674－5590（2017）03－0038－05

2016-05-20；

2016-07-06

国家自然科学基金项目（71401073）；南京航空航天大学研究生创新基地（实验室）开放基金项目（kfjj20160701）

赵权（1992—），男，湖北随州人，硕士研究生，研究方向为适航技术与管理.